Адиабатически изолированный сосуд разделен перегородкой
МГТУ им. Н. Э. Баумана
Домашнее задание №1
по термодинамике:
«Газовые смеси»
Вариант №15
Студент: Романов А.С.
Группа: Э7-52
Преподаватель: Чирков А.Ю.
-2012-
Условие задания:
Сосуд разделен адиабатной перегородкой на четыре части, в каждой из которых содержатся различные газы. После того как перегородка убрана, происходит «смешение в объеме» без теплообмена с окружающей средой. Состояния газов до смешения характеризуются следующими параметрами: массой mi0, кг; объемом Vi0, м3; температурой ti0, ˚С.
Необходимо определить:
температуру смеси после завершения процесса смешения t;
давление смеси Р, МПа;
газовую постоянную R, Дж/(кг*К);
среднюю молярную массу смеси µ, кг/моль;
объемный состав смеси {ri};
молярный состав смеси {ni};
парциальное давление компонентов смеси {pi}, МПа;
приведенные объемы компонентов смеси {Vi}, МПа;
истинную молярную теплоемкость смеси при р=const для температуры смеси, которая устанавливается после окончания процессов смешения ср ,Дж/(кмоль*К);
истинную объемную теплоемкость смеси при р=const после окончания процесса смешения C , Дж/(м *К);
истинную массовую теплоемкость смеси при р=const после окончания процесса смешения с, Дж/(кг*К);
количество теплоты Q (Дж), которое необходимо отвести от 3 кмоль смеси для охлаждения их при р=const до температуры смеси 300 К;
количество теплоты Q (Дж), которое необходимо отвести от 4 м смеси для охлаждения их при р=const до температуры смеси 300 К;
количество теплоты Q (Дж), которое необходимо отвести от 5 кг смеси для охлаждения их при р=const до температуры смеси 300 К.
Исходные данные:
Газ | mi0, кг | Vi0, м3 | ti0, ˚С |
O2 | 13 | 2,1 | 160 |
N2 | 16 | 1,6 | 260 |
H2 | 11 | 3,1 | 860 |
CO | 6 | 3,6 | 1060 |
Молярные массы газов:
; ; ;
Решение:
При получении значений из таблицы используется линейная интерполяция:
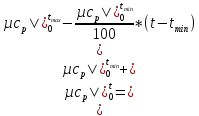 (1.1)
(1.1)
Температура смеси после завершения процесса смешения.
Нулевое приближение:
Первое приближение:
(1.2)
Вычислим теплоемкости, входящие формулу (1.2), необходимые для расчета суммарной внутренней энергии газов до смешения, а также температуры смеси в первом приближении:
O2:
СО2:
SO2:
H2O:
Подставим полученные значения:
кДж – суммарная внутренняя энергия газов до смешения (остаётся постоянной для всех последующих приближений).
Второе приближение:
(1.3)
Вычислим теплоемкости, входящие формулу (1.3):
O2:
СО2
SO2:
H2O:
Подставим полученные значения:
Третье приближение:
(1.3)
Вычислим теплоемкости, входящие формулу (1.3):
O2:
СО2
SO2:
H2O:
Подставим полученные значения:
Принимаем:
Давление смеси , МПа.
Для определения давления используем формулу:
где
– масса смеси;
– объем смеси;
– газовая постоянная смеси (см. пункт 3).
Тогда:
Постоянная газовая смеси .
где – массовая доля i-го газа.
Тогда:
,
Средняя молярная масса смеси – .
Состав смеси в объемных долях –
При одинаковых температуре и давлении всех газов одинаково, поэтому:
(см. пункт 6)
O2:
СО2:
SO2:
H2O:
Состав смеси в молярных долях – .
O2:
СО2:
SO2:
H2O:
Проверка: , верно.
Парциальные давления компонентов смеси – .
O2:
СО2:
SO2:
H2O:
Парциальные объемы компонентов смеси – .
O2:
СО2:
SO2:
H2O:
Истинная молярная теплоемкость смеси при , установившеюся после смешения .
O2:
СО2
SO2:
H2O:
Истинная объемная теплоемкость смеси при , установившеюся после смешения .
.
Истинная массовая теплоемкость смеси при , установившеюся после смешения .
.
Количество теплоты, которое необходимо отвести от 3 кмоль смеси для ее охлаждения при от температуры смеси до температуры .
Определим среднюю молярную теплоемкость смеси при процессе:
O2:
СО2
SO2:
H2O:
.
Кол-во теплоты, которое необходимо отвести от 4 м3 (н. у.) смеси для ее охлаждения при от температуры смеси до температуры
.
Определим среднюю объемную теплоемкость смеси при процессе:
.
.
Кол-во теплоты, которое необходимо отвести от 5кг смеси для ее охлаждения при от температуры смеси до температуры .
Определим среднюю массовую теплоемкость смеси при процессе:
Знак минус указывает на то, что теплота отводится от смеси.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
В параграфе 1.4 было введено понятие адиабатически изолированной системы, то есть системы, которая не обменивается теплотой с окружающими телами. Процессы, происходящие в такой системе, называются адиабатическими. Так как при адиабатических процессах , то первое начало термодинамики для них можно записать в форме:
. | (2.74) |
Совместное применение этого выражения и уравнения Клапейрона-Менделеева позволяет получить уравнение, описывающее адиабатический процесс в идеальном газе. Для этого представим выражение (2.74) в виде:
. | (2.75) |
Нахождение полных дифференциалов от правой и левой частей уравнения Клапейрона-Менделеева (2.10) дает:
. | (2.76) |
Вычитание из этой формулы выражения (2.75) приводит его к виду
. | (2.77) |
С учетом соотношения Майера (2.70) имеем:
. | (2.78) |
Умножим выражение (2.75) на отношение теплоемкостей и сложим его с формулой(2.78). Тогда получим
, | (2.79) |
где введено обозначение
. | (2.80) |
Величина называетсяпоказателем адиабаты. Формулы (2.65) и (2.71) позволяют определить показатель адиабаты через количество степеней свободы :
. | (2.81) |
Из этого выражения следует, что показатель адиабаты для идеального газа всегда больше единицы. Для одноатомных газов этот показатель равен 1,67, а для двухатомных и многоатомных соответственно 1,4 и 1,33.
Поделив уравнение (2.79) на произведение преобразуем его к виду
(2.82) |
или
. | (2.83) |
Отсюда следует:
. | (2.84) |
Интегрирование этого уравнения позволяет получить формулу
. | (2.85) |
которая называется уравнением Пуассона в честь французского механика, математика и физикаСимеона Дени Пуассона (1781 – 1840). Этоуравнение адиабатического процесса для идеального газа, или адиабаты – кривой, описываемой этим уравнением в переменных и.
С помощью уравнения Клапейрона-Менделеева уравнение (2.85) можно переписать, используя другие параметры состояния идеального газа:
, | (2.86) |
. | (2.87) |
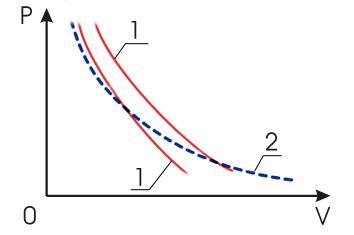
Сравнивая уравнение Пуассона (2.85) с уравнением Бойля-Мариотта (2.11): , можно убедиться, что адиабата идеального газа, построенная в координатахи, всегда идёт круче изотермы (см. рис. 2.7).
|
Рис. 2.7. Графики адиабатических процессов (1) и изотермического процесса (2) |
Это связано с тем, что, как указывалось выше, показатель адиабаты для газов всегда больше единицы и принимает наибольшее значение для одноатомных газов. Поэтому самую крутую адиабату имеют инертные газы, молекулы которых состоят из одного атома.
Поскольку адиабата пересекает все изотермы данной термодинамической системы, возможен адиабатический переход с одной изотермы на другую, путём сжатия или разрежения газа. А посредством изотермического изменения объёма возможен переход с одной адиабаты на другую.
Работу идеального газа в адиабатическом процессе можно определить с помощью выражения (2.74). Интегрирование (см. комментарий к формулам (1.6) – (1.8)) этого выражения дает:
, | (2.88) |
где: и- температуры газа в начале и в конце процесса соответственно. В данном случае работа при переходе из одного состояния системы в другое определяется только функцией состояния системы, так как путь перехода однозначно задан уравнением Пуассона.
Молярная теплоемкость газа может быть выражена через показатель адиабаты. Подстановка в формулу(2.80) соотношения Майера (2.70) приводит её к виду
, | (2.89) |
из которого следует искомое выражение:
. | (2.90) |
С учетом этой формулы выражение (2.88) может быть представлено в форме
. | (2.91) |
На основании уравнения адиабаты (2.86) запишем соотношение между температурами и объемами газа в начальном и конечном состояниях:
(2.92) |
или
. | (2.93) |
Подстановка этой формулы в выражение (2.91) дает
(2.94) |
или с учетом уравнения Клапейрона-Менделеева (2.10)
. | (2.95) |
Формула (2.95) может быть получена и непосредственно с помощью интеграла (1.13), при подстановке в него уравнения Пуассона (2.85), записанного для произвольной точки адиабаты
. | (2.96) |
Тогда имеем
. | (2.97) |
Адиабатический процесс может быть реализован в газе либо путём его термоизоляции, либо за счёт быстрого протекания процесса, когда процесс теплопередачи не успевает произойти. Первый способ применялся в опытах Джоуля, описанных выше, где было принципиально необходимо достижение газом состояния, близкого к равновесному. Поэтому каждый из опытов требовал продолжительного времени (около часа) и возникала необходимость введения поправок на тепловые потери.
Примером быстропротекающего процесса является распространение звука в воздухе. Несмотря на то, что такой процесс нельзя считать равновесным, опыт показывает, что для его описания возможно применение уравнения Пуассона, полученного в рамках равновесной термодинамики.
В 1816 году, за семь лет до вывода Пуассоном уравнения адиабатического процесса,Пьером Симоном Лапласом (1749 – 1827) была получена формула для скорости распространения звука в газе
, | (2.98) |
где: и- давление и плотность газа. Измерения значений,ипозволяют по этой формуле рассчитать значение показателя адиабаты. Для воздуха это значение близко к 1,4, что указывает на возможность с хорошей точностью считать его состоящим из двухатомных молекул.
Экспериментальное определение молярных теплоёмкостей идля реальных газов представляет собой довольно сложную задачу. Большой вклад в её решение внёсАнри Виктор Реньо (1810 – 1878), под руководством которого были измерены молярные теплоёмкости многих веществ, в том числе газов. Исследования проводились в лаборатории при Сервской фарфоровой мануфактуре и носили прикладной характер, связанный с совершенствованием тепловых машин. Некоторыми из методик, разработанных Ренье, впоследствии воспользовался Джоуль при проведении своих опытов.
В заключение рассмотрим вопрос о том, как соотносится уравнение Пуассона, записанное в переменных и(2.86), с результатами опытов Гей-Люссака, описанными в предыдущем параграфе. Действительно, в соответствии с результатами этих опытов температура идеального газа не изменяется при его расширении в жестком, адиабатически изолированном сосуде, а согласно уравнению (2.86) температура такого газа при адиабатическом процессе должна понижаться. Это кажущееся противоречие объясняется тем, что в соответствии со схемой опыта Гей-Люссака, показанной на рис. 2.5, идеальный газ при расширении не совершает механической работы над внешними телами: . Поэтому соотношение(2.74) сводится к тождеству: , и получение из него выражений(2.75) – (2.79) и далее формул (2.82) – (2.85) становится невозможным.
Таким образом, уравнение Пуассона неприменимо для описания опытов Гей-Люссака. Это связано с тем, что процесс адиабатического расширения идеального газа без совершения механической работы является необратимым, в отличие от обратимого адиабатического расширения, описываемого уравнением Пуассона. Подробнее описание необратимого адиабатического расширения рассмотрено в параграфе 4.3.
Задача 2.2. Внутри закрытого теплоизолированного цилиндрического сосуда находится теплонепроводящий поршень, который может двигаться без трения. В начальный момент поршень находится в середине сосуда и делит его на равные части объемом . В каждой из этих половин сосуда находится идеальный газ с показателем адиабаты при давлении . Какую работу надо совершить, чтобы уменьшить объём одной из половин в два раза?
Решение: В обеих частях цилиндрического сосуда будет происходить адиабатический процесс
,
где объёмы V1и V2 двух частей сосуда связаны соотношением
.
Пусть происходит уменьшение в два раза половины сосуда, описываемой объемом , то есть объем изменяется от до . Соответственно объем увеличивается от до . Тогда элементарная работа, совершаемая над газом, будет определяться разностью давлений в двух частях сосуда:
,
где учтено, что .
Подстановка в последнюю формулу первых двух соотношений и её интегрирование дает
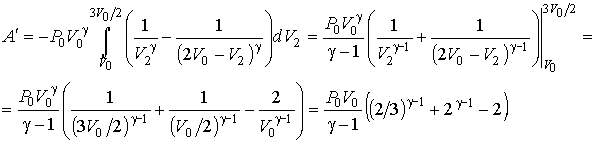
При это выражение равно нулю, в чем можно убедиться устремив к единице и раскрыв неопределенность. При это выражение становится положительным, так как при увеличении параметра второе слагаемое в этой формуле растёт быстрее, чем убывает первое.
Задача 2.3. Адиабатически изолированный сосуд разделен перегородкой на две равные части, каждая объемом . В левой части находится двухатомный идеальный газ при давлении и температуре . Торцевая стенка правой части сосуда является поршнем. Перегородку вынули, а затем газ медленно сжали поршнем так, что он снова стал занимать левую половину сосуда. Найти давления , и температуры , газа после изъятия перегородки и в конце процесса.
Решение: При адиабатическом расширении идеального газа без совершения работы над внешними телами, его внутренняя энергия и температура не изменяются. Поэтому после изъятия перегородки имеем:
,
.
При адиабатическом сжатии газа поршнем увеличение его внутренней энергии равно работе, совершенной поршнем. Температура и давление газа в конце процесса могут быть найдены с помощью соотношений (2.86)и (2.85), из которых имеем:
,
.
Отметим, что хотя протекающие процессы при расширении газа и его сжатии различные, уравнение состояния идеального газа применимо для описания конечного состояния газа для обоих этих случаев. Расширение газа после удаления перегородки будет необратимым, а его медленное сжатие поршнем – можно описывать как обратимый процесс. Возможность использования уравнения состояния идеального газа для описания конечного состояния необратимого процесса связано с предположением о том, что при достижении этого конечного состояния газ становится термодинамически равновесной системой.
Соседние файлы в предмете Термодинамика
- #
- #
- #
- #
- #
- #
Источник
В параграфе 1.4 было введено понятие адиабатически изолированной системы, то есть системы, которая не обменивается теплотой с окружающими телами. Процессы, происходящие в такой системе, называются адиабатическими. Так как при адиабатических процессах , то первое начало термодинамики для них можно записать в форме:
. | (2.74) |
Совместное применение этого выражения и уравнения Клапейрона-Менделеева позволяет получить уравнение, описывающее адиабатический процесс в идеальном газе. Для этого представим выражение (2.74) в виде:
. | (2.75) |
Нахождение полных дифференциалов от правой и левой частей уравнения Клапейрона-Менделеева (2.10) дает:
. | (2.76) |
Вычитание из этой формулы выражения (2.75) приводит его к виду
. | (2.77) |
С учетом соотношения Майера (2.70) имеем:
. | (2.78) |
Умножим выражение (2.75) на отношение теплоемкостей и сложим его с формулой(2.78). Тогда получим
, | (2.79) |
где введено обозначение
. | (2.80) |
Величина называетсяпоказателем адиабаты. Формулы (2.65) и (2.71) позволяют определить показатель адиабаты через количество степеней свободы :
. | (2.81) |
Из этого выражения следует, что показатель адиабаты для идеального газа всегда больше единицы. Для одноатомных газов этот показатель равен 1,67, а для двухатомных и многоатомных соответственно 1,4 и 1,33.
Поделив уравнение (2.79) на произведение преобразуем его к виду
(2.82) |
или
. | (2.83) |
Отсюда следует:
. | (2.84) |
Интегрирование этого уравнения позволяет получить формулу
. | (2.85) |
которая называется уравнением Пуассона в честь французского механика, математика и физикаСимеона Дени Пуассона (1781 – 1840). Этоуравнение адиабатического процесса для идеального газа, или адиабаты – кривой, описываемой этим уравнением в переменных и.
С помощью уравнения Клапейрона-Менделеева уравнение (2.85) можно переписать, используя другие параметры состояния идеального газа:
, | (2.86) |
. | (2.87) |
Сравнивая уравнение Пуассона (2.85) с уравнением Бойля-Мариотта (2.11): , можно убедиться, что адиабата идеального газа, построенная в координатахи, всегда идёт круче изотермы (см. рис. 2.7).
|
Рис. 2.7. Графики адиабатических процессов (1) и изотермического процесса (2) |
Это связано с тем, что, как указывалось выше, показатель адиабаты для газов всегда больше единицы и принимает наибольшее значение для одноатомных газов. Поэтому самую крутую адиабату имеют инертные газы, молекулы которых состоят из одного атома.
Поскольку адиабата пересекает все изотермы данной термодинамической системы, возможен адиабатический переход с одной изотермы на другую, путём сжатия или разрежения газа. А посредством изотермического изменения объёма возможен переход с одной адиабаты на другую.
Работу идеального газа в адиабатическом процессе можно определить с помощью выражения (2.74). Интегрирование (см. комментарий к формулам (1.6) – (1.8)) этого выражения дает:
, | (2.88) |
где: и- температуры газа в начале и в конце процесса соответственно. В данном случае работа при переходе из одного состояния системы в другое определяется только функцией состояния системы, так как путь перехода однозначно задан уравнением Пуассона.
Молярная теплоемкость газа может быть выражена через показатель адиабаты. Подстановка в формулу(2.80) соотношения Майера (2.70) приводит её к виду
, | (2.89) |
из которого следует искомое выражение:
. | (2.90) |
С учетом этой формулы выражение (2.88) может быть представлено в форме
. | (2.91) |
На основании уравнения адиабаты (2.86) запишем соотношение между температурами и объемами газа в начальном и конечном состояниях:
(2.92) |
или
. | (2.93) |
Подстановка этой формулы в выражение (2.91) дает
(2.94) |
или с учетом уравнения Клапейрона-Менделеева (2.10)
. | (2.95) |
Формула (2.95) может быть получена и непосредственно с помощью интеграла (1.13), при подстановке в него уравнения Пуассона (2.85), записанного для произвольной точки адиабаты
. | (2.96) |
Тогда имеем
. | (2.97) |
Адиабатический процесс может быть реализован в газе либо путём его термоизоляции, либо за счёт быстрого протекания процесса, когда процесс теплопередачи не успевает произойти. Первый способ применялся в опытах Джоуля, описанных выше, где было принципиально необходимо достижение газом состояния, близкого к равновесному. Поэтому каждый из опытов требовал продолжительного времени (около часа) и возникала необходимость введения поправок на тепловые потери.
Примером быстропротекающего процесса является распространение звука в воздухе. Несмотря на то, что такой процесс нельзя считать равновесным, опыт показывает, что для его описания возможно применение уравнения Пуассона, полученного в рамках равновесной термодинамики.
В 1816 году, за семь лет до вывода Пуассоном уравнения адиабатического процесса,Пьером Симоном Лапласом (1749 – 1827) была получена формула для скорости распространения звука в газе
, | (2.98) |
где: и- давление и плотность газа. Измерения значений,ипозволяют по этой формуле рассчитать значение показателя адиабаты. Для воздуха это значение близко к 1,4, что указывает на возможность с хорошей точностью считать его состоящим из двухатомных молекул.
Экспериментальное определение молярных теплоёмкостей идля реальных газов представляет собой довольно сложную задачу. Большой вклад в её решение внёсАнри Виктор Реньо (1810 – 1878), под руководством которого были измерены молярные теплоёмкости многих веществ, в том числе газов. Исследования проводились в лаборатории при Сервской фарфоровой мануфактуре и носили прикладной характер, связанный с совершенствованием тепловых машин. Некоторыми из методик, разработанных Ренье, впоследствии воспользовался Джоуль при проведении своих опытов.
В заключение рассмотрим вопрос о том, как соотносится уравнение Пуассона, записанное в переменных и(2.86), с результатами опытов Гей-Люссака, описанными в предыдущем параграфе. Действительно, в соответствии с результатами этих опытов температура идеального газа не изменяется при его расширении в жестком, адиабатически изолированном сосуде, а согласно уравнению (2.86) температура такого газа при адиабатическом процессе должна понижаться. Это кажущееся противоречие объясняется тем, что в соответствии со схемой опыта Гей-Люссака, показанной на рис. 2.5, идеальный газ при расширении не совершает механической работы над внешними телами: . Поэтому соотношение(2.74) сводится к тождеству: , и получение из него выражений(2.75) – (2.79) и далее формул (2.82) – (2.85) становится невозможным.
Таким образом, уравнение Пуассона неприменимо для описания опытов Гей-Люссака. Это связано с тем, что процесс адиабатического расширения идеального газа без совершения механической работы является необратимым, в отличие от обратимого адиабатического расширения, описываемого уравнением Пуассона. Подробнее описание необратимого адиабатического расширения рассмотрено в параграфе 4.3.
Задача 2.2. Внутри закрытого теплоизолированного цилиндрического сосуда находится теплонепроводящий поршень, который может двигаться без трения. В начальный момент поршень находится в середине сосуда и делит его на равные части объемом . В каждой из этих половин сосуда находится идеальный газ с показателем адиабаты при давлении . Какую работу надо совершить, чтобы уменьшить объём одной из половин в два раза?
Решение: В обеих частях цилиндрического сосуда будет происходить адиабатический процесс
,
где объёмы V1и V2 двух частей сосуда связаны соотношением
.
Пусть происходит уменьшение в два раза половины сосуда, описываемой объемом , то есть объем изменяется от до . Соответственно объем увеличивается от до . Тогда элементарная работа, совершаемая над газом, будет определяться разностью давлений в двух частях сосуда:
,
где учтено, что .
Подстановка в последнюю формулу первых двух соотношений и её интегрирование дает

При это выражение равно нулю, в чем можно убедиться устремив к единице и раскрыв неопределенность. При это выражение становится положительным, так как при увеличении параметра второе слагаемое в этой формуле растёт быстрее, чем убывает первое.
Задача 2.3. Адиабатически изолированный сосуд разделен перегородкой на две равные части, каждая объемом . В левой части находится двухатомный идеальный газ при давлении и температуре . Торцевая стенка правой части сосуда является поршнем. Перегородку вынули, а затем газ медленно сжали поршнем так, что он снова стал занимать левую половину сосуда. Найти давления , и температуры , газа после изъятия перегородки и в конце процесса.
Решение: При адиабатическом расширении идеального газа без совершения работы над внешними телами, его внутренняя энергия и температура не изменяются. Поэтому после изъятия перегородки имеем:
,
.
При адиабатическом сжатии газа поршнем увеличение его внутренней энергии равно работе, совершенной поршнем. Температура и давление газа в конце процесса могут быть найдены с помощью соотношений (2.86)и (2.85), из которых имеем:
,
.
Отметим, что хотя протекающие процессы при расширении газа и его сжатии различные, уравнение состояния идеального газа применимо для описания конечного состояния газа для обоих этих случаев. Расширение газа после удаления перегородки будет необратимым, а его медленное сжатие поршнем – можно описывать как обратимый процесс. Возможность использования уравнения состояния идеального газа для описания конечного состояния необратимого процесса связано с предположением о том, что при достижении этого конечного состояния газ становится термодинамически равновесной системой.
Соседние файлы в предмете Механика
- #
- #
- #
- #
- #
- #
Источник