Алеша боря и гриша нашли старинный сосуд таблица истинности

Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Подробный алгоритм решения логической задачи в виде презентации. Условие задачи: Алёша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения: 1) Алеша: «Это сосуд греческий и изготовлен в V веке». 2) Боря: «Это сосуд финикийский и изготовлен в III веке». 3) Гриша: «Это сосуд не греческий и изготовлен в IV веке». Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
2 слайд

Описание слайда:
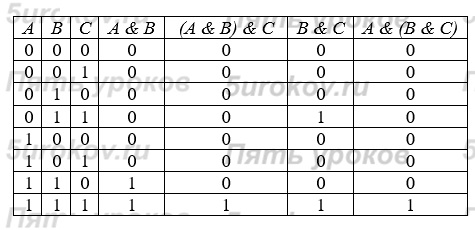
Решение Запишем условие задачи в виде таблицы
3 слайд

Описание слайда:
Поработаем с высказываниями мальчиков и сделаем следующее сосуд греческий Получили противоречие сосуд оказался выполнен в III и IV веке одновременно, чего быть не может. Вывод наше предположение не верно!
4 слайд

Описание слайда:
Поработаем с высказываниями мальчиков и сделаем следующее сосуд финикийский Получили, что наше предположение оказалось верным и не ведет к противоречию. Ответ: сосуд изготовлен в Финикии в V веке.
5 слайд

Описание слайда:
2. Разработайте задание по теме “Логика” для закрепления изученного материала. В качестве задачи на уроке логики можно разобрать следующую: В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что: Смит самый высокий; играющий на скрипке меньше ростом играющего на флейте; играющие на скрипке и флейте и Браун любят пиццу; когда между альтистом и трубачом возникает ссора, Смит мирит их; Браун не умеет играть ни на трубе, ни на гобое. На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель информатики

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Краткое описание документа:
Данная методическая разработка содержит подробный алгоритм решения логической задачи в виде презентации. Рекомендуется к использованию на уроках по теме “Логика” в 5-7 классах.
Условие задачи:
Алёша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
1) Алеша: «Это сосуд греческий и изготовлен в V веке».
2) Боря: «Это сосуд финикийский и изготовлен в III веке».
3) Гриша: «Это сосуд не греческий и изготовлен в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Оставьте свой комментарий
Источник
- 1
- 2
- 3
- 4
- 5
3.8/5, Голосов: 6
Задание 1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?
Скачать презентацию
Да, дополняет. Приведены ученые, кто занимался логикой, дано определение алгебры, есть дополнительные примеры. И много другое.
Задание 2. Объясните, почему следующие предложения не являются высказываниями.
а) Какого цвета этот дом? – это вопрос, не утверждение.
б) Число X не превосходит единицы. – мы не знаем число Х, поэтому не можем оценить – правда это или ложь.
в) 4Х + 3. – это вообще даже не уравнение, что уж тут говорить о правде.
г) Посмотрите в окно. – побуждение к действию не является высказыванием.
д) Пейте томатный сок! – побуждение к действию не является высказыванием.
е) Эта тема скучна. – это субъективное мнение, которое не может быть однозначно классифицировано как правда или ложь, т.к. не подтверждена фактами , кроме того, не известно, о какой теме идет речь.
ж) Рикки Мартин – самый популярный певец. – это субъективное мнение, которое не может быть однозначно классифицировано как правда или ложь, т.к. не подтверждена фактами.
з) Вы были в театре? – вопросительное высказывание не является высказыванием.
Задание 3. Приведите по одному примеру истинных и ложных высказываний из биологии, географии, информатики, истории, математики, литературы.
• Биология:
1) За мягким нёбом, а также у входа в пищевод и гортань находятся миндалины.
2) Грипп – хроническое заболевание, когда миндалины воспаляются, становятся отёчными и болезненными. (ЛОЖЬ, т.к. это тонзиллит).
• География:
1) Столица Италии – Париж. (ЛОЖЬ, т.к. это Рим, а Париж во Франции)
2) Выделяют 4 основные стороны света – север, юг, запад, восток.
• Информатика:
1) Инверсия – это логическое отрицание.
2) Конъюнкция – это логическое сложение. (ЛОЖЬ, т.к. это дизъюнкция является логическим сложением)
• История:
1) Промышленная революция (конец XVIII – первая половина XIX в.) началась в Англии в последней трети XVIII в.
2) Во времена аграрной революции в Англии в конце XVIII века землей владели фермеры, которые сдавали ее в аренду за определенную плату. (ЛОЖЬ, т.к. владели лендлорды, а фермеры были арендаторы)
• Математика:
1) У треугольника 5 сторон.
2) Квадрат гипотенузы равен сумме квадратов двух катетов.
• Литература:
1) Народные частушки – небольшие лирические песни, обычно имеющие форму четырехстрочного рифмованного куплета.
2) Первые упоминания о частушках относятся к 60-м годам XII века. (ЛОЖЬ, т.к это поздний жанр, появившийся только в XIX веке)
Задание 4. В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание.
1) Число 376 чётное и трёхзначное.
А = Число 376 чётное
В = Число 376 трёхзначное
A & B
2) Зимой дети катаются на коньках или на лыжах.
A = Зимой дети катаются на коньках
B = Зимой дети катаются на лыжах
A | B
3) Новый год мы встретим на даче или на Красной площади.
A = Новый год мы встретим на даче.
B = Новый год мы встретим на Красной площади.
A | B
4) Неверно, что Солнце движется вокруг Земли.
A = Солнце движется вокруг Земли
¬A
5) Земля имеет форму шара, который из космоса кажется голубым.
A = Земля имеет форму шара, который из космоса кажется голубым.
B = Шар из космоса кажется голубым.
A & B
6) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.
A = На уроке математики старшеклассники отвечали на вопросы учителя
B = На уроке математики старшеклассники писали самостоятельную работу
A & B
Задание 5. Постройте отрицания следующих высказываний.
а) Сегодня в театре НЕ идёт опера «Евгений Онегин».
б) НЕ каждый охотник желает знать, где сидит фазан.
в) Число 1 НЕ простое число.
г) Натуральные числа, оканчивающиеся цифрой 0, являются простыми числами.
д) Число 3 НЕ является делителем числа 198.
е) Коля решил НЕ все задания контрольной работы.
ж) НЕ во всякой школе некоторые ученики интересуются спортом.
Во всякой школе некоторые ученики НЕ интересуются спортом.
з) Некоторые млекопитающие живут на суше.
Задание 6. Пусть А = «Ане нравятся уроки математики», а В = «Ане нравятся уроки химии». Выразите следующие формулы на обычном языке:
а) А & В;
Ане нравятся уроки математики и химии.
б) ¬А & В;
Ане НЕ нравятся уроки математики и нравятся уроки химии.
в) А & ¬В;
Ане нравятся уроки математики, а химии – не нравятся.
г) A ˅ B
Ане нравятся уроки математики или химии.
д) A ˅ ¬B
Ане нравятся уроки математики или не нравятся уроки химии.
е) ¬А ˅ В;
Ане не нравятся уроки математики или нравятся уроки химии.
ж) ¬(А & В);
Неверно, что Ане нравятся уроки математики И химии.
з) ¬(A ˅ В)
Неверно, что Ане нравятся уроки математики ИЛИ химии.
и) ¬(А&¬В).
Неверно, что Ане нравятся уроки математики и не нравятся уроки химии.
Задание 7. Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:
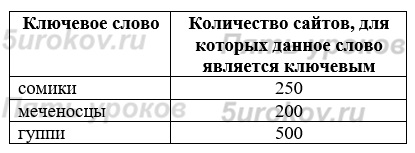
Дано дополнительно помимо таблицы:
сомики & гуппи – 0 сайтов;
сомики & меченосцы – 20 сайтов;
меченосцы & гуппи – 10 сайтов.
1) Найти:
Сколько сайтов будет найдено по запросу сомики | меченосцы | гуппи?
С | M | Г = ?
Нарисуем круги Эйлера:
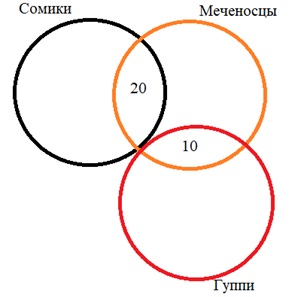
Чтобы найти количество сайтов, соответствующих этому запросу, к количеству элементов множества сомики (250) добавим количество элементов множества меченосцы без сомиков (200 – 20), а также гуппи без меченосцев (500 – 10).
Получаем: 250 + 180 + 490 = 920 сайтов
Ответ: 920 сайтов
2) Найти:
Для скольких сайтов рассматриваемого сегмента ложно высказывание «Сомики — ключевое слово сайта ИЛИ меченосцы — ключевое слово сайта ИЛИ гуппи — ключевое слово сайта»?
То есть это по сути всё, что не вошло в наш С | М | Г, то есть надо найти ¬(С | M | Г).
С | M | Г = 920
По условию задачи сегмент сети Интернет состоит из 1000 сайтов.
То есть, то, что не вошло в нашу область это 1000 – 920 = 80 сайтов.
Ответ: 80 сайтов
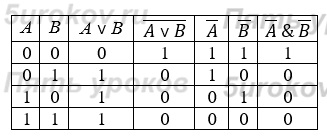
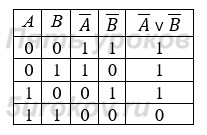
Задание 8. Постройте таблицы истинности для следующих логических выражений:
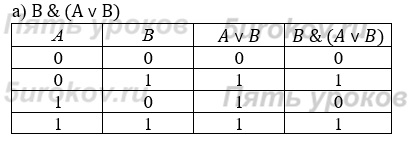
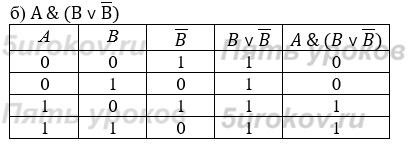
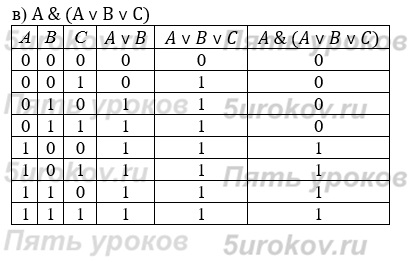
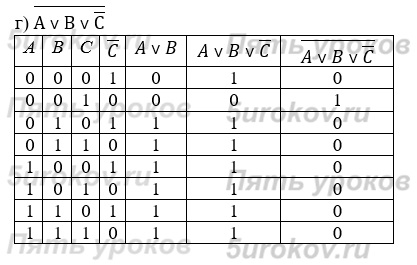
Задание 9. Проведите доказательство рассмотренных в параграфе логических законов с помощью таблиц истинности.
1) Переместительный (коммутативный) закон:
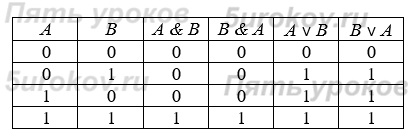
2) Сочетательный (ассоциативный закон):
для логического умножения:

для логического сложения:
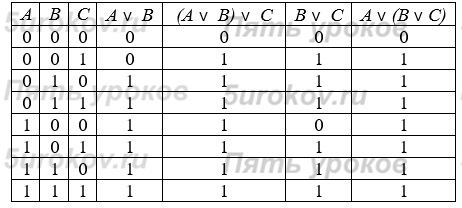
3) Распределительный (дистрибутивный) закон:
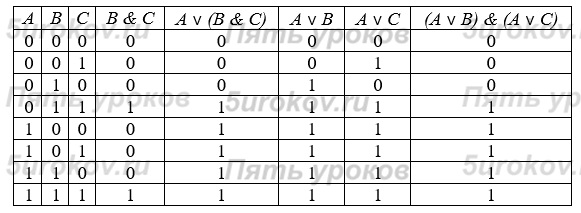
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
4) Закон двойного отрицания:
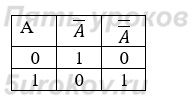
5) Закон исключенного третьего:
6) Закон повторения:
7) Закон операций с 0 и 1:
8) Законы общей инверсии:
а) для логического умножения:
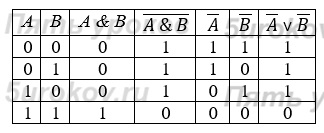
б) для логического сложения:
Задание 10. Даны три числа в десятичной системе счисления: A=23, B=19, C=26. Переведите A, B и C в двоичную систему счисления и выполните поразрядной логические операции (A ˅ B) & C. Ответ дайте в десятичной системе счисления.
Переведём числа в двоичную систему счисления:
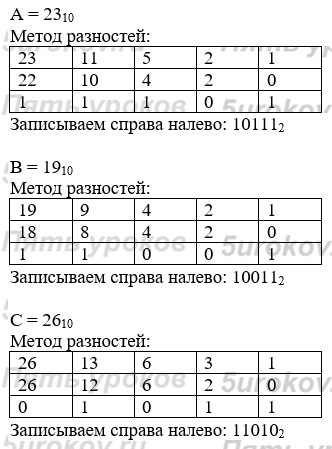
A = 23 = 101112
B = 19 = 100112
C = 26 = 110102
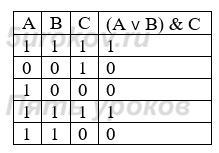
Ответ: 100102 = 1810
Задание 11. Найдите значения выражений:
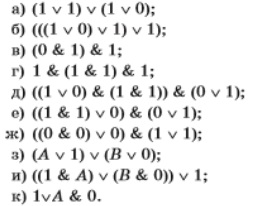
а) Все сложения, если есть хоть одна 1, то будет 1. Ответ 1
б) Все сложения, если есть хоть одна 1, то будет 1. Ответ 1
в) Все умножения, если есть хоть один 0, то будет 0. Ответ 0
г) Все умножения, если НЕТ ни одного 0, то будет 1. Ответ 1
д) Умножения скобок, если есть хоть один 0, то будет 0. Ту нужно посмотреть каждую скобку. Первая и третья есть 1, поэтому 1, вторая умножение 1 и 1, тоже будет 1. Следовательно, все скобки по 1, нет 0, поэтому Ответ 1
е) Тоже нужно проверить каждую скобку, т.к. умножение. Ответ 1
ж) Проверяем каждую скобку. Первая половина будет умножение 0, сумма с 0 будет 0, поэтому общее умножение тоже 0. Ответ 0
з) Все сложения, если есть хоть одна 1, будет 1. Ответ 1
и) Чтобы там не получалось в скобках последним действием идет сложение с 1, поэтому ответ будет 1.
к) Так как последним действием будет сложение с 1, ответ будет 1.
Задание 12. Найдите значение логического выражения для указанных значений числа Х:
а) 1; б) 2; в) 3; г) 4.
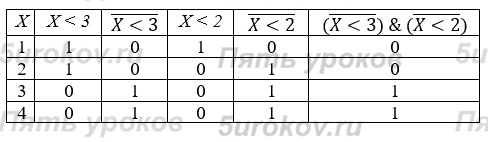
Ответ: а) 0; б) 0; в) 1; г) 1.
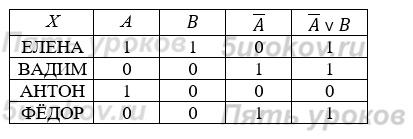
Задание 13. Пусть А = «Первая буква имени – гласная», В = «Четвертая буква имени согласная». Найдите значение логического выражения для следующих имён:
а) ЕЛЕНА
б) ВАДИМ
в) АНТОН
г) ФЁДОР
Задание 14. Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:
Смит: «Я не делал этого. Браун сделал это.»
Джон: «Браун не виновен. Смит сделал это.»
Браун: «Я не делал этого. Джон не делал этого.»
Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду. Кто из подозреваемых должен быть оправдан?
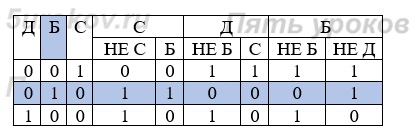
Итог: утаил клад Браун, остальные должны быть оправданы.
Ответ: Смит и Джон.
Задание 15. Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения… Где и в каком веке изготовлен сосуд?
Только в 1 прав, в другом не прав, следовательно, иcходя из 2 логических принципов составляем уравнение:
• 0 v 1 = 1
• 1 & 1=1
Усл. Обозначения:
Г – греческий, Ф – Финикийский, Цифра – век
(Г или 5)&(Ф или 3)&(неГ или 4)=1
Распределительный закон, раскрываем скобки:
(ГФ или Г3 или Ф5 или 53) & (неГ или 4)=1
ГФ и 53 обнуляем, т.к. это ложь (0), не может быть одновременно и то, и другое правдой. С тем, что осталось еще раз распределительный закон, раскрываем скобки:
(Г3 и неГ) или Г34 или (Ф5 и неГ) или Ф54 = 1
Г и неГ не может быть одновременно, обнуляем
Г34 обнуляем, Ф54 обнуляем.
Остается:
Ф5 и неГ = 1
Ответ: Финикийский сосуд, изготовлен в V веке.
Задание 16. Выясните, какой сигнал должен быть на выходе электронной схемы при каждом возможном наборе сигналов на входах. Составьте таблицу работы схемы. Каким логическим выражением описывается схема?
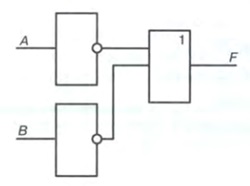
Логическое выражение:
Таблица работы схемы:
Задание 17. Пусть М = {1, 2, 3, 4, 5, 6}, K = {1, 3, 5}, P = {2, 4, 6, 7, 8}. Запишите с помощью фигурных скобок область истинности предложений:
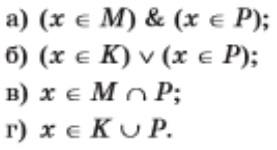
а) {2, 4, 6}
б) {1, 2, 3, 4, 5, 6, 7, 8}
в) {2, 4, 6}
г) {1, 2, 3, 4, 5, 6, 7, 8}
Решение заданий из учебника Информатика 8 класс Босова, параграф 1.4 Элементы алгебры логики. Высказывание, логические операции, построение таблиц истинности для логических выражений, свойства логических операций, решение логических задач, логические элементы.
Источник
1
Решение логических задач
2
Способы решения задач Алгебраический способ (с помощью алгебры высказываний или таблиц истинности) 1) выделить элементарные (простые) высказывания и обозначить их буквами; 2) записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций; 3) составить единое логическое выражение для всех требований задачи; 4) используя законы алгебры логики, упростить полученное выражение и вычислить все его значения либо построить таблицу истинности для рассматриваемого выражения; 5) выбрать решение – набор значений простых высказываний, при котором логическое выражение является истинным; 6) проверить, удовлетворяет ли полученное решение условию задачи.
3
Табличный способ Нагляден, но не обладает универсальностью, т. к. предназначен для решения только определенного класса задач. Кроме того он требует анализа находящихся в таблице информации, умения сравнивать и сопоставлять.
4
Графический способ Метод графов применяется тогда, когда между объектами существует много связей. Граф позволяет наглядно представить эти связи и определить, какие из них не противоречат условиям задачи. Метод диаграмм Эйлера-Венна позволяет графически решать математические задачи на основе применения теории множеств.
5
Задача 1. «Сосуд» Условие задачи: Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по 2 предположения: Алеша: «Этот сосуд греческий и изготовлен в V веке». Боря: Этот сосуд финикийский и изготовлен в III веке». Гриша: «Этот сосуд не греческий и изготовлен в IV веке». Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
6
1 способ. Решим задачу с помощью алгебры высказываний 1) Переведем условие задачи на язык логики высказываний (выделим простые высказывания и обозначим их буквами). Пусть А – сосуд греческий; В – сосуд финикийский; С3 – сосуд изготовлен в 3 веке; С4 – сосуд изготовлен в 4 веке; С5 – сосуд изготовлен в 5 веке.
7
2) Запишем условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций. Алеша прав: А=1 или С5=1, т.е. А & ¬С5۷ ¬А & С5 = 1. Боря прав: В=1 или С3=1, т.е. В & ¬С3۷ ¬В & С3 = 1. Гриша прав: не А=1 или С4=1, т.е. ¬А & ¬С4۷ А & С5 = 1. Сосуд может быть изготовлен только в одном из веков, т.е. С3 & С4 & ¬С5۷ С3 & ¬С4 & С5۷ ¬С3 & С4 & С5 = 1. и только в одной из стран, т.е. В &¬А۷ ¬В & А = 1.
8
3) Составим единое логическое выражение для всех требований задачи. Получили 5 тождественно истинных высказываний, их логически перемножаем. Результат должен быть тождественно истинным высказыванием. (А & ¬С5۷ ¬А & С5) & (В & ¬С3۷ ¬В & С3) & & (¬А & ¬С4۷ А & С5) & (В &¬А۷ ¬В & А) & & (С3 & С4 & ¬С5۷ С3 & ¬С4 & С5۷ ¬С3 & С4 &С5)= 1
9
4) Используя законы алгебры логики, упростим полученное выражение и вычислим все его значения. Умножим скобки: 1 на 3 и 2 на 4, получаем: (А & С4 & ¬С5۷ ¬А & ¬С4 & С5)&(В &¬А & ¬С3۷ ¬В & А & С3) & & (С3 & С4 & ¬С5۷ С3 & ¬С4 & С5۷ ¬С3 & С4 &С5) = = (А & С4 & ¬С5 & ¬В & С3۷ В &¬А & ¬С3 & С4 & ¬С5) & & (С3 & С4 & ¬С5۷ С3 & ¬С4 & С5۷ ¬С3 & С4 &С5) = = ¬В &А & С3 & С4 & ¬С5۷ В &¬А & ¬С3 & ¬С4 & С5 = = 0 ۷ В &¬А & ¬С3& ¬С4 & С5 = В &¬А & ¬С3 & ¬С4 & С5
10
5) Выбираем решение, при котором логическое выражение является истинным В &¬А & ¬С3 & ¬С4 & С5. 6) Проверяем, удовлетворяет ли полученное решение условию задачи и делаем вывод сосуд финикийский изготовлен в 5 веке.
11
2 способ. Решим задачу с помощью таблицы Пусть Алеша: «Этот сосуд греческий и изготовлен в V веке» = А. Боря: Этот сосуд финикийский и изготовлен в III веке» = Б. Гриша: «Этот сосуд не греческий и изготовлен в IV веке» = Г. 3 век 4 век 5 век греческийАА,Б,ГБ финикийскийГБА,Б,Г Получаем противоречие высказыванию Гриши. Вывод: сосуд финикийский изготовлен в 5 веке.
12
Задача 2. «Компьютер» Условие задачи: Компьютер вышел из строя (нет изображения на экране монитора), однако неизвестно какое устройство не работает (монитор, видеокарта или оперативная память). Можно предположить следующее: – Если монитор не исправен или видеокарта неисправна, то оперативная память неисправна; – Если монитор исправен, то оперативная память исправна. Исправен ли монитор?
13
Решим задачу с помощью таблицы истинности 1) Переведем условие задачи на язык логики высказываний (выделим простые высказывания и обозначим их буквами). Пусть А – монитор неисправен; В – видеокарта неисправна; С – оперативная память неисправна. 2) Запишем условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций. (¬А۷ В) С и ¬А ¬С 3) Составим единое логическое выражение для всех требований задачи. Пусть F (A, B, C) = ((¬А۷ В) С) & (¬А ¬С).
14
4) Составим для данного высказывания таблицу истинности: F (A, B, C) = ((¬А۷ В) С) & (¬А ¬С) АВС¬А¬А ۷ В(¬А ۷ В) С ¬С ¬А ¬С F (A,B,C)
15
5) Выбираем решение, при котором логическое выражение является истинным. Решить данную задачу – значит указать, при каких значениях А полученное сложное высказывание истинно. Необходимо проанализировать все строки таблицы истинности, где F = 1. Анализ таблицы показывает, что сложное высказывание истинно во всех случаях, когда А – истинно, т.е. вероятнее всего неисправен монитор. 6) Проверяем, удовлетворяет ли полученное решение условию задачи и делаем вывод неисправен монитор.
16
Задача 3. «Ученики» Условие задачи: В классе 36 человек. Ученики этого класса посещают математические, физический и химический кружки, причем математический кружок посещают 18 человек, физический – 14, химический кроме того известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 – и математический и химический, 3 – и физический и химический. Сколько учеников класса не посещают никаких кружков?
17
Решим задачу с помощью кругов Эйлера-Венна Множество всех учеников класса на рисунке изобразим большим кругом. Внутри круга расположим три пересекающихся круга меньшего диаметра: М – круг изображает множество членов математического кружка; Ф – физического кружка; X – химического кружка. МФ Х
18
МФ Х Дадим имена множествам. Пусть МФХ – множество ребят, каждый из которых посещает все 3 кружка. МФ – множество занимающихся и в математическом, и в физическом кружке (и, возможно, также в химическом). МФ¬Х – и в математическом, и в физическом, но не в химическом и т. д. МФХМФХ МФ¬ХМФ¬Х Впишем нужные имена множеств в области, изображенные на рисунке: М¬ФХМ¬ФХ ¬МФХ¬МФХ М¬Ф¬ХМ¬Ф¬Х ¬МФ¬Х¬МФ¬Х ¬М¬ФХ¬М¬ФХ ¬М¬Ф¬Х¬М¬Ф¬Х
19
В область МФХ впишем число 2, так как все три кружка посещают 2 ученика. Теперь обратимся к числовым данным. Множество МФ состоит из 8 человек. Но это множество является объединением множеств МФХ и МФ¬Х, причем в МФХ входят 2 человека. Значит, на долю МФ¬Х остается 6 человек. Теперь рассмотрим множество MX, состоящее из 5 человек. Оно также состоит из двух частей: на МФХ приходится 2 человека, значит, на М¬ФХ – 3. Рассмотрим теперь множество М, в которое входят 18 учеников. Оно состоит из четырех частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в подмножество М¬Ф¬X, входит 18 – ( ) = 7 человек. Аналогично определим количество учащихся в множествах ¬МФХ, ¬МФ¬Х, ¬М¬ФХ. Три пересекающихся круга образуют 7 непересекающихся областей, изображающих непересекающиеся подмножества учеников, каждый из которых посещает хотя бы 1 кружок. Просуммируем цифры в этих областях: = 28 человек посещает кружки. Значит, = 8 ребят не посещают никаких кружков. Ответ: в классе 8 учеников, не посещающих кружки. МФХМФХ МФ¬ХМФ¬Х М¬ФХМ¬ФХ ¬МФХ¬МФХ М¬Ф¬ХМ¬Ф¬Х ¬МФ¬Х¬МФ¬Х ¬М¬ФХ¬М¬ФХ ¬М¬Ф¬Х¬М¬Ф¬Х МФ Х
Источник
