Алеша боря и гриша нашли в земле старинный сосуд таблица

Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Подробный алгоритм решения логической задачи в виде презентации. Условие задачи: Алёша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения: 1) Алеша: «Это сосуд греческий и изготовлен в V веке». 2) Боря: «Это сосуд финикийский и изготовлен в III веке». 3) Гриша: «Это сосуд не греческий и изготовлен в IV веке». Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
2 слайд

Описание слайда:
Решение Запишем условие задачи в виде таблицы
3 слайд

Описание слайда:
Поработаем с высказываниями мальчиков и сделаем следующее сосуд греческий Получили противоречие сосуд оказался выполнен в III и IV веке одновременно, чего быть не может. Вывод наше предположение не верно!
4 слайд

Описание слайда:
Поработаем с высказываниями мальчиков и сделаем следующее сосуд финикийский Получили, что наше предположение оказалось верным и не ведет к противоречию. Ответ: сосуд изготовлен в Финикии в V веке.
5 слайд

Описание слайда:
2. Разработайте задание по теме “Логика” для закрепления изученного материала. В качестве задачи на уроке логики можно разобрать следующую: В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что: Смит самый высокий; играющий на скрипке меньше ростом играющего на флейте; играющие на скрипке и флейте и Браун любят пиццу; когда между альтистом и трубачом возникает ссора, Смит мирит их; Браун не умеет играть ни на трубе, ни на гобое. На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Выберите книгу со скидкой:
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА
Инфолавка – книжный магазин для педагогов и родителей от проекта «Инфоурок»

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель информатики

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Краткое описание документа:
Данная методическая разработка содержит подробный алгоритм решения логической задачи в виде презентации. Рекомендуется к использованию на уроках по теме “Логика” в 5-7 классах.
Условие задачи:
Алёша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предположения:
1) Алеша: «Это сосуд греческий и изготовлен в V веке».
2) Боря: «Это сосуд финикийский и изготовлен в III веке».
3) Гриша: «Это сосуд не греческий и изготовлен в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Оставьте свой комментарий
Источник
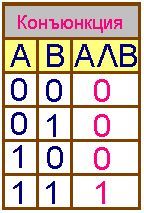
(логическое умножение)
F =
А
Λ
B
Составное высказывание, образованное в
результате операции логического умножения (конъюнкции),
истинно тогда и только тогда, когда истинны входящие в него
простые высказывания.
Например, рассмотрим составное
высказывание “2*2=4 и 3*3=10”. Первое
простое высказывание (2*2=4) истинно (А=1),
а второе высказывание (3*3=10) ложно (В=0),
по таблице определяем, что логическая функция принимает значение
ложь (F=0), т.е.
данное составное высказывание ложно.
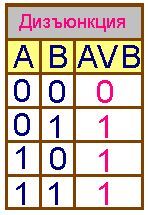
(логическое сложение)
F =
А
V
B
результате
операции логического сложения (дизъюнкции),
истинно тогда, когда истинны хотя бы одно из входящих в него
простых высказываний.
Например, рассмотрим составное высказывание
“2*2=4 или 3*3=10”. Первое простое
высказывание (2*2=4) истинно (А=1), а
второе высказывание (3*3=10) ложно (В=0),
по таблице определяем, что логическая функция принимает значение
истина (F=1),
т.е. данное составное высказывание истинно.
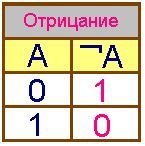
(логическое отрицание)
F =
¬А
(инверсия) делает истинное высказывание
ложным и, наоборот, ложное – истинным.
Например,
А=(2*2=4)=1(ИСТИНА)
¬А
= 0
В=(3*3=10)=0(ЛОЖЬ)
¬В = 1

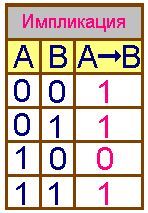
(логическое следование)
F =
А
=>
B
результате
операции логического следование (импликации),
ложна тогда и только тогда, когда из истинной предпосылки (первого
высказывания) следует ложный вывод (второе высказывание).
Логическое следование(импликация) образуется соединением
двух высказываний в одно с помощью оборота речи “если…,
то …”
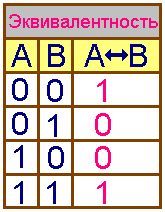
(логическое равенство)
F =
А
<=>
B
помощью
логической
операции эквивалентности, истинно тогда и только тогда,
когда оба высказывания одновременно либо ложны, либо истинны.
Логическое равенство(эквивалентность) образуется
соединением двух высказываний в одно с помощью оборота речи
“…тогда и только тогда, когда
…”
преобразования логических выражений
- ¬¬А
= А (закон двойного отрицание) - ¬(А
Λ В)
= ¬А
V ¬B
( законы - ¬(А
V В)
= ¬А
Λ ¬B
Моргана) - А =>
В = ¬А
V
B - ¬(А =>
В) = А
Λ ¬B - А <=>
В =(А
Λ
B) V (¬А
Λ ¬B) - А
Λ ¬А
= 0 (закон непротиворечия) - А
V
¬А
= 1 (закон
исключенного третьего)
(А
Λ В)
≡ (В
Λ
А) ;
(А
V
В) ≡ (В
V
А) ;
Законы ассоциативности:
(А V
В) V С ≡
А V (В V
С);
(А Λ
В) Λ С ≡
А Λ (В Λ
С);
Законы дистрибутивности:
А Λ (В
V С) ≡ (А Λ
В) V (А Λ
С)
А V (В
Λ С) ≡ (А V
В) Λ (А V
С)
таблицы истинности данной функции, которая
показывает какие значения принимает логическая функция при всех
возможных наборах её аргументов.
Задача №43 стр. 59 :
Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая
удивительную находку, каждый высказал по два предложения:
Алеша: “Это сосуд греческий и изготовлен в V
веке”. Боря: “Это сосуд финикийский и изготовлен
в III веке”. Гриша: “Это сосуд не
греческий и изготовлен в IV веке”. Учитель
истории сказал ребятам, что каждый из них прав только в одном из двух
предложений. Где и в каком веке изготовлен сосуд?
Решение:
А = “Это
сосуд греческий”;
B
= ” Изготовлен в V
веке”;
C
= ” Изготовлен в IV веке
“;
D
= “Изготовлен в III
веке”;
E
= “Это сосуд финикийский “.
| А | В | С | D | E | |
| Алеша | + | + | |||
| Боря | + | + | |||
| Гриша | – | + |
1. Если А =1(истина) , то В=0; А=1,то Е=0,
тогда D=1;
¬А=0, С=0, а это не
может быть, по условию ¬А или С истина.
2. Пусть А=0 и В=1; Тогда
Е=1 а D=0; и
¬А=1, то С=0;
в итоге получим В=1 и Е=1, т. е. сосуд
финикийский и изготовлен в
V веке.
В нарушении правил обмена валюты
подозреваются четыре работника банка – А, В, С и D.
Известно, что:
- Если А нарушил, то и В нарушил правила обмена валюты.
- Если В нарушил, то и С нарушил или А не нарушил.
- Если D не нарушил, то А нарушил, а С
не нарушил. - Если D нарушил, то и А нарушил.
Кто из подозреваемых нарушил правила обмена валюты? Решите
задачу с помощью логических операций.
Решение:
- А => B;
- B => C V
¬А; - ¬D => A Λ
¬C; - D => A
Произведение всех высказываний =1.
( А
=> B)Λ(B
=> C V
¬А)Λ(¬D
=> A Λ ¬C)Λ (D
=> A) = 1
а
выражение справедлива тогда и только тогда, когда
А => B = 1;
B => C V
¬А)
= 1; ¬D => A Λ ¬C = 1;
D => A = 1;
Составим таблицу истинности
для этого выражения:
A | B | C | D | А => B | D => A | C V ¬А) | B => C V ¬А) | A Λ ¬C | ¬D => A Λ ¬C | F |
| 1 | 1 | 1 | 1 | |||||||
| 1 | 1 | 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Ответ: А=1,B=1,C=1,D=1,
т.е. все подозреваемые нарушили правила обмена валюты.
Источник
1
Решение логических задач
2
Способы решения задач Алгебраический способ (с помощью алгебры высказываний или таблиц истинности) 1) выделить элементарные (простые) высказывания и обозначить их буквами; 2) записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций; 3) составить единое логическое выражение для всех требований задачи; 4) используя законы алгебры логики, упростить полученное выражение и вычислить все его значения либо построить таблицу истинности для рассматриваемого выражения; 5) выбрать решение – набор значений простых высказываний, при котором логическое выражение является истинным; 6) проверить, удовлетворяет ли полученное решение условию задачи.
3
Табличный способ Нагляден, но не обладает универсальностью, т. к. предназначен для решения только определенного класса задач. Кроме того он требует анализа находящихся в таблице информации, умения сравнивать и сопоставлять.
4
Графический способ Метод графов применяется тогда, когда между объектами существует много связей. Граф позволяет наглядно представить эти связи и определить, какие из них не противоречат условиям задачи. Метод диаграмм Эйлера-Венна позволяет графически решать математические задачи на основе применения теории множеств.
5
Задача 1. «Сосуд» Условие задачи: Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по 2 предположения: Алеша: «Этот сосуд греческий и изготовлен в V веке». Боря: Этот сосуд финикийский и изготовлен в III веке». Гриша: «Этот сосуд не греческий и изготовлен в IV веке». Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
6
1 способ. Решим задачу с помощью алгебры высказываний 1) Переведем условие задачи на язык логики высказываний (выделим простые высказывания и обозначим их буквами). Пусть А – сосуд греческий; В – сосуд финикийский; С3 – сосуд изготовлен в 3 веке; С4 – сосуд изготовлен в 4 веке; С5 – сосуд изготовлен в 5 веке.
7
2) Запишем условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций. Алеша прав: А=1 или С5=1, т.е. А & ¬С5۷ ¬А & С5 = 1. Боря прав: В=1 или С3=1, т.е. В & ¬С3۷ ¬В & С3 = 1. Гриша прав: не А=1 или С4=1, т.е. ¬А & ¬С4۷ А & С5 = 1. Сосуд может быть изготовлен только в одном из веков, т.е. С3 & С4 & ¬С5۷ С3 & ¬С4 & С5۷ ¬С3 & С4 & С5 = 1. и только в одной из стран, т.е. В &¬А۷ ¬В & А = 1.
8
3) Составим единое логическое выражение для всех требований задачи. Получили 5 тождественно истинных высказываний, их логически перемножаем. Результат должен быть тождественно истинным высказыванием. (А & ¬С5۷ ¬А & С5) & (В & ¬С3۷ ¬В & С3) & & (¬А & ¬С4۷ А & С5) & (В &¬А۷ ¬В & А) & & (С3 & С4 & ¬С5۷ С3 & ¬С4 & С5۷ ¬С3 & С4 &С5)= 1
9
4) Используя законы алгебры логики, упростим полученное выражение и вычислим все его значения. Умножим скобки: 1 на 3 и 2 на 4, получаем: (А & С4 & ¬С5۷ ¬А & ¬С4 & С5)&(В &¬А & ¬С3۷ ¬В & А & С3) & & (С3 & С4 & ¬С5۷ С3 & ¬С4 & С5۷ ¬С3 & С4 &С5) = = (А & С4 & ¬С5 & ¬В & С3۷ В &¬А & ¬С3 & С4 & ¬С5) & & (С3 & С4 & ¬С5۷ С3 & ¬С4 & С5۷ ¬С3 & С4 &С5) = = ¬В &А & С3 & С4 & ¬С5۷ В &¬А & ¬С3 & ¬С4 & С5 = = 0 ۷ В &¬А & ¬С3& ¬С4 & С5 = В &¬А & ¬С3 & ¬С4 & С5
10
5) Выбираем решение, при котором логическое выражение является истинным В &¬А & ¬С3 & ¬С4 & С5. 6) Проверяем, удовлетворяет ли полученное решение условию задачи и делаем вывод сосуд финикийский изготовлен в 5 веке.
11
2 способ. Решим задачу с помощью таблицы Пусть Алеша: «Этот сосуд греческий и изготовлен в V веке» = А. Боря: Этот сосуд финикийский и изготовлен в III веке» = Б. Гриша: «Этот сосуд не греческий и изготовлен в IV веке» = Г. 3 век 4 век 5 век греческийАА,Б,ГБ финикийскийГБА,Б,Г Получаем противоречие высказыванию Гриши. Вывод: сосуд финикийский изготовлен в 5 веке.
12
Задача 2. «Компьютер» Условие задачи: Компьютер вышел из строя (нет изображения на экране монитора), однако неизвестно какое устройство не работает (монитор, видеокарта или оперативная память). Можно предположить следующее: – Если монитор не исправен или видеокарта неисправна, то оперативная память неисправна; – Если монитор исправен, то оперативная память исправна. Исправен ли монитор?
13
Решим задачу с помощью таблицы истинности 1) Переведем условие задачи на язык логики высказываний (выделим простые высказывания и обозначим их буквами). Пусть А – монитор неисправен; В – видеокарта неисправна; С – оперативная память неисправна. 2) Запишем условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций. (¬А۷ В) С и ¬А ¬С 3) Составим единое логическое выражение для всех требований задачи. Пусть F (A, B, C) = ((¬А۷ В) С) & (¬А ¬С).
14
4) Составим для данного высказывания таблицу истинности: F (A, B, C) = ((¬А۷ В) С) & (¬А ¬С) АВС¬А¬А ۷ В(¬А ۷ В) С ¬С ¬А ¬С F (A,B,C)
15
5) Выбираем решение, при котором логическое выражение является истинным. Решить данную задачу – значит указать, при каких значениях А полученное сложное высказывание истинно. Необходимо проанализировать все строки таблицы истинности, где F = 1. Анализ таблицы показывает, что сложное высказывание истинно во всех случаях, когда А – истинно, т.е. вероятнее всего неисправен монитор. 6) Проверяем, удовлетворяет ли полученное решение условию задачи и делаем вывод неисправен монитор.
16
Задача 3. «Ученики» Условие задачи: В классе 36 человек. Ученики этого класса посещают математические, физический и химический кружки, причем математический кружок посещают 18 человек, физический – 14, химический кроме того известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 – и математический и химический, 3 – и физический и химический. Сколько учеников класса не посещают никаких кружков?
17
Решим задачу с помощью кругов Эйлера-Венна Множество всех учеников класса на рисунке изобразим большим кругом. Внутри круга расположим три пересекающихся круга меньшего диаметра: М – круг изображает множество членов математического кружка; Ф – физического кружка; X – химического кружка. МФ Х
18
МФ Х Дадим имена множествам. Пусть МФХ – множество ребят, каждый из которых посещает все 3 кружка. МФ – множество занимающихся и в математическом, и в физическом кружке (и, возможно, также в химическом). МФ¬Х – и в математическом, и в физическом, но не в химическом и т. д. МФХМФХ МФ¬ХМФ¬Х Впишем нужные имена множеств в области, изображенные на рисунке: М¬ФХМ¬ФХ ¬МФХ¬МФХ М¬Ф¬ХМ¬Ф¬Х ¬МФ¬Х¬МФ¬Х ¬М¬ФХ¬М¬ФХ ¬М¬Ф¬Х¬М¬Ф¬Х
19
В область МФХ впишем число 2, так как все три кружка посещают 2 ученика. Теперь обратимся к числовым данным. Множество МФ состоит из 8 человек. Но это множество является объединением множеств МФХ и МФ¬Х, причем в МФХ входят 2 человека. Значит, на долю МФ¬Х остается 6 человек. Теперь рассмотрим множество MX, состоящее из 5 человек. Оно также состоит из двух частей: на МФХ приходится 2 человека, значит, на М¬ФХ – 3. Рассмотрим теперь множество М, в которое входят 18 учеников. Оно состоит из четырех частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в подмножество М¬Ф¬X, входит 18 – ( ) = 7 человек. Аналогично определим количество учащихся в множествах ¬МФХ, ¬МФ¬Х, ¬М¬ФХ. Три пересекающихся круга образуют 7 непересекающихся областей, изображающих непересекающиеся подмножества учеников, каждый из которых посещает хотя бы 1 кружок. Просуммируем цифры в этих областях: = 28 человек посещает кружки. Значит, = 8 ребят не посещают никаких кружков. Ответ: в классе 8 учеников, не посещающих кружки. МФХМФХ МФ¬ХМФ¬Х М¬ФХМ¬ФХ ¬МФХ¬МФХ М¬Ф¬ХМ¬Ф¬Х ¬МФ¬Х¬МФ¬Х ¬М¬ФХ¬М¬ФХ ¬М¬Ф¬Х¬М¬Ф¬Х МФ Х
Источник

