Алгебра концентрация кислоты в сосуде
1. Все рассматриваемые смеси (сплавы, растворы)
однородны.
2. Не делается различия между литром как
единицей емкости и литром как единицей массы.
Если смесь (сплав, раствор) массы m состоит из
веществ А, В, С (которые имеют массы
соответственно а, в, с) то величина (соответственно , ) называется концентрацией
вещества А (соответственно В, С ).
Величина *
100% (соответственно * 100%, * 100%) называется процентным содержанием
вещества А (соответственно В,
С). + + =
1.
При составлении уравнения обычно прослеживают
содержание какого-нибудь одного вещества из тех,
которые смешиваются ( сплавляются и т. п. ).
В задачах на составление уравнений и
неравенств полезным оказываются всевозможные
таблицы, диаграммы и схемы. Это необходимо, как
чертеж при решении геометрической задачи.
Оформление первого этапа математического
моделирования задач на «смеси и сплавы» в виде
таблиц способствует более глубокому
пониманию процесса решения такого типа задач.
Практически для всех рассмотренных задач
удалось составить таблицу. Рассмотрим
примеры типовых задач ГИА.
Имеется 200г 30%-го раствора уксусной
кислоты. Сколько г воды нужно добавить к этому
раствору, чтобы получить 6%-ный раствор
уксусной кислоты?
Решение.
х г воды надо добавить к раствору.
| Процентное содержание кислоты | Вес раствора, г | Вес кислоты, г | |
| Данный раствор | 30% | 200 | 200 * 0,3 |
| Новый раствор | 6% | 200 + х | 0,06(200 + х) |
0,06(200 + х) = 60,
200 + х = 1000,
х = 800. 800г воды надо добавить.
Ответ: 800г.
Сколько г сахарного сиропа, концентрация
которого 25%, надо добавить к 200 г воды, чтобы в
полученном растворе содержание сахара
составляло 5%.
Решение.
| Процентное содержание сахара | Вес раствора, г | Вес сахара, г | |
| Сироп | 25% | х | 0,25х |
| Новый раствор | 5% | 200 + х | 0,05(200 + х) |
0,25х = 0,05(200 + х),
5х = 200 х,
4х = 200,
х = 50. 50г сиропа надо добавить.
Ответ: 50г.
Сколько г 15%-ного раствора соли надо
добавить к 50 г 60%-ного раствора соли, чтобы
получить 40%-ный раствор соли.
Решение.
| Процентное содержание соли | Вес раствора, г | Вес соли, г | |
| Первый раствор | 15% | х | 0,15х |
| Второй раствор | 60% | 50 | 0,6 * 50 |
| Смесь | 40% | х + 50 | 0,4(х + 50) |
0,4(х + 50) = 0,15х + 30,
0,4х + 20 = 0,15х + 30,
0,25х = 10,
х =
40.
40 г 15%-ного раствора соли надо добавить.
Ответ: 40г.
Имеются два сосуда, содержащих 4 кг и 6 кг
раствора кислоты разных концентраций. Если их
слить вместе, то получится раствор, содержащий 35%
кислоты. Если же слить равные массы этих
растворов, то получится раствор, содержащий 36%
кислоты. Сколько кг кислоты содержится в каждом
сосуде?
Решение.
Первая ситуация.
| Процентное содержание кислоты | Вес раствора, кг | Вес кислоты, кг | |
| Первый раствор | х% | 4 | 0,01х * 4 |
| Второй раствор | у% | 6 | 0,01у * 6 |
| Смесь | 35% | 10 | 0,35 * 10 |
0,04х + 0,06у = 3,5.
Вторая ситуация.
| Процентное содержание кислоты | Вес раствора, кг | Вес кислоты, кг | |
| Первый раствор | х% | m | 0,01 хm |
| Второй раствор | у% | m | 0,01 уm |
| Смесь | 36% | 2m | 0,36 * 2m |
0,01хm + 0,01уm = 0,72m,
0,01х + 0,01у = 0,72.
Решая систему из составленных уравнений,
получаем
х = 41 и у =
31.
0,41 * 4 = 1,64(кг) в первом сосуде.
0,31 * 6 = 1,86(кг) во втором сосуде.
Ответ: 1,64 кг. 1,86 кг.
В первом сплаве содержится 25% меди, а во втором
– 45%. В каком отношении надо взять
первый и второй сплавы, чтобы получить из них
новый сплав, содержащий 30% меди?
Решение.
| Процентное содержание меди | Вес сплава | Вес меди | |
| Первый сплав | 25% | х | 0,25х |
| Второй сплав | 45% | у | 0.45у |
| Новый сплав | 30% | х+у | 0,3(х + у) |
0,25х + 0,45у = 0,3(х + у),
– 0,05х = – 0,15у,
х = 3у. х : у = 3 : 1.
Ответ: 3 : 1.
В куске сплава меди и цинка количество меди
увеличили на 40%, а количество цинка уменьшили на
40%. В результате общая масса куска сплава
увеличилась на 20%. Определите процентное
содержание меди и цинка в первоначальном куске
сплава.
Решение.
| Вес меди | Вес цинка | Вес сплава | |
| Данный сплав | х | у | х + у |
| Новый сплав | х + 0,4х | у – 0,4у | 1,2(х + у) |
1,4х + 0,6у = 1,2(х + у),
0,2х = 0,6у,
х = 3у,
х : у = 3 :
1.
100 : 4 * 3 = 75(%),
100 – 75 = 25(%).
Ответ: 25%, 75%.
Сплав золота с серебром, содержащий 80 г
золота, сплавлен со 100 г чистого золота. В
результате содержание золота в сплаве
повысилось по сравнению с первоначальным на 20%.
Сколько серебра в сплаве?
Решение.
– = 20,
х = 120.120 кг серебра в сплаве.
Ответ: 120 кг.
Литература.
1. М.Н. Кочагина , В.В.Кочагин.
Математика: 9 класс: Подготовка к « малому
ЕГЭ», Москва. Эксмо, 2008.
2. Л.В.Кузнецова и др. Алгебра: сборник
заданий для подготовки к государственной
итоговой аттестации. Москва. «Просвещение». 2011.
3. Учебно-методическое пособие под редакцией
Ф.Ф. Лысенко. Алгебра 9 класс. Подготовка к
итоговой аттестации. Ростов-на-Дону, 2010.
4. В.Н.Литвиненко, А.Г. Мордкович.
Практикум по элементарной математике. Москва.
«Просвещение». 1991.
Приложение 1
Источник
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 – x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 – x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 – x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 – x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 – x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 – x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
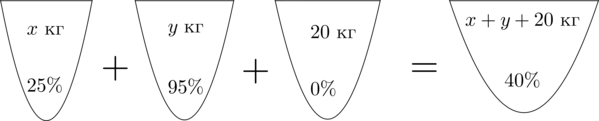
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
Аналогично составим схему, описывающую получение (50)-процентного раствора:
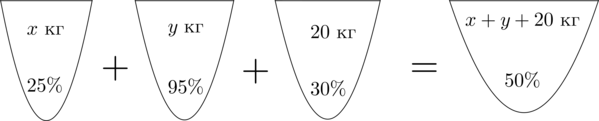
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20
Источник

ЗНАЕТЕ ЛИ ВЫ?
Цель работы: изучить способы выражения концентрации растворов, научиться рассчитывать концентрацию растворов.
Задание: приготовить приблизительно 0,1 н раствор соляной кислоты и установить нормальность и титр кислоты. Выполнить требования к результатам работы, оформить отчет, решить задачу.
Теоретическое введение
Один из методов определения концентрации растворов – объемный анализ. Он сводится к измерению объемов реагирующих веществ, концентрация одного из которых известна.
Такое измерение производится постепенным прибавлением одного раствора к другому до окончания реакции. Этот процесс называется титрованием. Окончание реакции определяется с помощью индикатора.
При определении объемов растворов целесообразно использовать следующие способы выражения концентрации растворов:
Молярная концентрация эквивалентов вещества Вили нормальность( (В) или н) – отношение количества эквивалентов растворенного вещества к объему раствора:
, моль/л,
где nэк(В) – количество эквивалентов вещества В, моль; mB – масса вещества В, г; Мэк(В) – молярная масса эквивалентов вещества В, г/моль; Vр – объем раствора, л.
Массовая доля растворенного вещества В(ωВ) – отношение (обычно – процентное) массы растворенного вещества к массе раствора:
,
где mB – масса вещества В, г; mр – масса раствора, г.
Если выражать массу раствора через его плотность (ρ) и объем (Vр), то
Титр раствора вещества В(ТВ) показывает массу растворенного вещества, содержащегося в 1 мл (см3) раствора:
, г/мл,
где mB – масса растворенного вещества В, г; Vp – объем раствора, мл.
Титр также можно рассчитать по формуле:
, г/мл,
где Мэк(В) – молярная масса эквивалентов вещества В, г/моль; (В) – молярная концентрация эквивалентов, моль/л.
Выполнение работы
Опыт 1. Приготовление приблизительно 0,1 н раствора соляной кислоты
Налить (под тягой) в цилиндр концентрированный раствор соляной кислоты и ареометром определить его плотность. По измеренной плотности по таблице 1 найти массовую долю (%) кислоты в растворе. Рассчитать массу кислоты, необходимую для приготовления 250 мл 0,1 н раствора HCl по формуле:
, откуда m = сэк · Мэк(HCl) · V,
где m – масса кислоты, г; Мэк(HCl) – молярная масса эквивалентов кислоты, г/моль; сэк – молярная концентрация эквивалентов, моль/л; V – объем кислоты, л.
Полученную величину (m) пересчитать на объем, который требуется для приготовления 250 мл 0,1 н раствора кислоты по формуле:
, откуда V = ,
где V – объем кислоты, мл; m – масса кислоты,г; ω – массовая доля в % HCl, найденная по таблице 1; ρ – плотность кислоты, г/см3, измеренная ареометром.
Пипеткой отобрать рассчитанный объем раствора кислоты, перенести его в мерную колбу, разбавить водой до метки и хорошо перемешать.
Опыт 2. Установление нормальности и титра кислоты
Отмерить пипеткой 10 мл приготовленного раствора кислоты, перенести его в коническую колбу, добавить 1-2 капли фенолфталеина.
В бюретку налить 0,1 н раствор NaOH. Оттитровать раствор кислоты. Для этого медленно приливать из бюретки щелочь в колбу с раствором кислоты, непрерывно перемешивая его в процессе титрования. Место, в которое падают капли щелочи, окрашивается в розовый цвет, исчезающий при взбалтывании. Титрование проводить до тех пор, пока от одной капли щелочи раствор примет неисчезающую окраску. Титрование повторить. Результаты не должны отличаться более чем на 0,1 мл.
Требования к результату опыта:
Данные опыта занести в таблицу:
| № п/п | V (HCl) (объем кислоты) | V (NaOH) (объем щелочи) | Vср (NaOH) (среднее значение объема щелочи) |
Вычислить:
1. Молярную концентрацию эквивалентов раствора кислоты по закону эквивалентов:
сэк (HCl)∙V(HCl) = сэк (NaOH)∙V(NaOH), откуда
, моль/л
где сэк (HCl) и сэк (NaOH) – молярные концентрации эквивалентов растворов; V(HCl) и V(NaOH) – объемы реагирующих растворов.
2. Титр раствора НСl по формуле:
, г/мл
Таблица 1.
Плотность раствора соляной кислоты
| Плотность ρ, г/см3 | Массовая доля кислоты, % |
| 1,100 | 20,01 |
| 1,105 | 20,97 |
| 1,110 | 21,92 |
| 1,115 | 22,86 |
| 1,120 | 23,82 |
| 1,125 | 24,78 |
| 1,130 | 25,75 |
| 1,135 | 26,70 |
| 1,140 | 27,66 |
| 1,145 | 28,61 |
| 1,150 | 29,57 |
| 1,155 | 30,55 |
| 1,160 | 31,52 |
| 1,165 | 32,49 |
| 1,170 | 33,46 |
| 1,175 | 34,42 |
| 1,180 | 35,39 |
| 1,185 | 36,31 |
| 1,190 | 37,23 |
| 1,195 | 38,16 |
| 1,200 | 39,11 |
Примеры решения задач
В химической практике наиболее употребительны следующие способы выражения концентрации растворов:
Молярная концентрация вещества Вилимолярность(сВ или М) – отношение количества растворенного вещества к объему раствора:
, моль/л, (1)
где nB – количество вещества В, моль; mB – масса вещества В, г; МВ – молярная масса вещества В, г/моль; Vр – объем раствора, л.
Молярная концентрация эквивалентов вещества Вили нормальность( (В) или н) – отношение количества эквивалентов растворенного вещества к объему раствора:
, моль/л, (2)
где nэк(В) – количество эквивалентов вещества В, моль; mB – масса вещества В, г; Мэк(В) – молярная масса эквивалентов вещества В, г/моль; Vр – объем раствора, л.
Моляльная концентрация вещества Вили моляльность(сm(B)) – отношение количества растворенного вещества к массе растворителя:
, моль/кг, (3)
где nВ – количество вещества В, моль; mB – масса вещества В,г; mS – масса растворителя, г; МВ – молярная масса вещества В, г/моль.
Массовая доля растворенного вещества В(ωВ) – отношение (обычно – процентное) массы растворенного вещества к массе раствора:
, (4)
где mB – масса вещества В, г; mр – масса раствора, г.
Если выражать массу раствора через его плотность (ρ) и объем (Vр), то
(5)
Молярная (мольная) доля вещества В(хВ, безразмерная величина ) ─ отношение количества данного вещества к суммарному количеству всех веществ, составляющих раствор, включая растворитель.
Если раствор состоит из одного растворенного вещества и растворителя, то молярная доля вещества (хВ) равна:
, (6)
а молярная доля растворителя (хs):
, (7)
где nB – количество растворенного вещества, моль; nS – количество вещества растворителя, моль.
Сумма молярных долей всех веществ раствора равна единице.
Титр раствора вещества В(ТВ) показывает массу растворенного вещества, содержащегося в 1 мл (см3) раствора:
, г/мл, (8)
где mB – масса растворенного вещества В, г; Vp – объем раствора, мл.
Титр также можно рассчитать по формулам:
, г/мл, (9)
где Мэк(В) – молярная масса эквивалентов вещества В, г/моль; (В) – молярная концентрация эквивалентов, моль/л;
, г/мл, (10)
где ωВ – массовая доля вещества В; ρ – плотность раствора, г/см3.
Пример 5.1. Водный раствор содержит 354 г H3PO4 в 1 л. Плотность раствора ρ = 1,18 г/мл. Вычислить: а) массовую долю (%) H3PO4 в растворе;
б) молярную концентрацию; в) молярную концентрацию эквивалентов;
г) моляльность; д) титр; е) молярные доли H3PO4 и Н2О.
Решение. а) Для расчета массовой доли воспользуемся формулой (5):
%
б) Молярная масса H3PO4 равна 98 г/моль. Молярную концентрацию раствора находим из соотношения (1):
= 3,61 моль/л.
в) Молярная масса эквивалентов H3PO4 равна 32,7 г/моль. Молярную концентрацию эквивалентов рассчитываем по формуле (2):
= 10,83 моль/л.
г) Для определения моляльности по формуле (3) необходимо рассчитать массу растворителя в растворе. Масса раствора составляет 1,18 ∙ 1000 = 1180 г.
Масса растворителя в растворе mS = 1180 – 354 = 826 г.
Моляльная концентрация раствора равна:
4,37 моль/кг
д) Титр раствора можно рассчитать по формулам (8), (9), (10):
= 0,354 г/мл,
0,354 г/мл,
0,354 г/мл.
е) В 1 л раствора содержится 3,61 моль H3PO4 (см. пункт б).
Масса растворителя в растворе 826 г, что составляет 45,9 моль.
Молярные доли H3PO4 и Н2О рассчитываем по формулам (6) и (7):
0,073;
0,927.
Пример 5.2. Сколько миллилитров 50 %-ного раствора HNO3, плотность которого 1,32 г/мл, требуется для приготовления 5 л 2 %-ного раствора, плотность которого 1,01 г/мл?
Решение. При решении задачи пользуемся формулой (5). Сначала находим массу азотной кислоты в 5 л 2 %-ного раствора:
101 г.
Чтобы ответить на вопрос задачи, надо определить, в каком объеме раствора с массовой долей HNO3 50 % содержится 101 г HNO3:
153 мл
Таким образом, для приготовления 5 л 2 %-ного раствора HNO3 требуется 153 мл 50 %-ного раствора HNO3.
Пример 5.3. На нейтрализацию 50 мл раствора кислоты израсходовано
25 мл 0,5 н раствора щелочи. Чему равна нормальность кислоты?
Решение. Так как вещества взаимодействуют между собой в эквивалентных количествах, то можно написать
VA ∙ cэк(А) = VB ∙ сэк(B)
50 ∙ сэк(кислоты) = 25 ∙ 0,5, отсюда
сэк(кислоты) = 0,25 моль/л
Следовательно, для реакции был использован 0,25 н раствор кислоты.
Задачи
5.1. В одном литре раствора содержится 10,6 г карбоната натрия Na2CO3. Рассчитать молярную концентрацию, молярную концентрацию эквивалентов и титр раствора. (Ответ: 0,1 М; 0,2 н; 10,6∙10-3 г/мл)
5.2. Вычислить молярную концентрацию и молярную концентрацию эквивалентов 20 %-ного раствора хлорида кальция плотностью 1,178 г/мл.
(Ответ: 2,1 М; 4,2 н).
5.3. Сколько моль HNO3 содержится в 250 мл раствора с массовой долей кислоты 30 % и плотностью, равной 1,18 г/мл? (Ответ: 1,40 моль).
5.4. Водный раствор содержит 5 г CuSO4 в 45 г воды. Плотность раствора равна 1,107 г/мл. Вычислить массовую долю (%) CuSO4 в растворе, а также моляльность и мольные доли CuSO4 и Н2О.
(Ответ: 9 %; 0,694 моль/кг; 0,012; 0,988).
5.5. Вычислить титры растворов: а) 0,05 М NaCl; б) 0,004 н Ca(OH)2;
в) 30 %-ного КОН, ρ = 1,297 г/мл.
(Ответ: а) 0,00292 г/мл; б) 0,148 ∙ 10‾3 г/мл; в) 0,389 г/мл).
5.6. Чему равна нормальность 30 %-ного раствора NaOH плотностью 1,328 г/мл? К 1 л этого раствора прибавили 5 л воды. Получился раствор плотностью 1,054 г/мл. Вычислить массовую долю (%) NaOH в полученном растворе. (Ответ: 9,96 н; 6,3 %).
5.7. В 1 кг воды растворили 666 г КОН, плотность раствора равна 1,395 г/мл. Вычислить массовую долю КОН в полученном растворе, молярность и мольные доли щелочи и воды. (Ответ: 40 %; 9,96 моль/л; 0,176; 0,824).
5.8. Какой объем 2 М раствора К2СО3 надо взять для приготовления 1 л 0,25 н раствора? (Ответ: 62,5 мл).
5.9. Из 600 г 5 %-ного раствора сульфата меди упариванием удалили 100 г воды. Чему равна массовая доля CuSO4 в оставшемся растворе? (Ответ: 6 %).
5.10. Какой объем 50 %-ного КОН (ρ = 1,538 г/мл) требуется для приготовления 3 л 6 %-ного раствора (ρ = 1,048 г/мл)? (Ответ: 245,3 мл).
5.11. Из 5 л раствора гидроксида калия с массовой долей КОН 50 % и плотностью 1,538 г/мл надо приготовить раствор с массовой долей КОН 18 %. Какой объем воды потребуется? (Ответ: 17,5 л).
5.12. Вычислить моляльную и молярную концентрацию эквивалентов 20,8 %-ного раствора HNO3 плотностью 1,12 г/мл. Сколько граммов кислоты содержится в 4 л этого раствора? (Ответ: 4,17 моль/кг; 3,7 н; 931,84 г).
5.13. Сколько миллилитров 0,2 М раствора Na2CO3 требуется для реакции с 50 мл 0,5 М раствора CaCl2? (Ответ: 125 мл).
5.14. Плотность 15 %-ного раствора Н2SO4 1,105 г/мл. Вычислить молярность, моляльность и молярную концентрацию эквивалентов раствора серной кислоты. (Ответ: 1,69 моль/л; 1,8 моль/кг; 3,38 моль/л).
5.15. Сколько миллилитров раствора соляной кислоты с плотностью 1,195 г/мл, содержащей 38 % HCl, нужно для приготовления 1 л 2 н раствора?
(Ответ: 160,7 мл).
5.16. При растворении 18 г Н3РО4 в 282 мл воды получили раствор фосфорной кислоты, плотность которого 1,031 г/мл. Вычислить молярную, моляльную, молярную концентрацию эквивалентов полученного раствора и его титр. (Ответ: 0,63 М; 0,65 моль/кг; 1,89 н; 0,062 г/мл).
5.17. На нейтрализацию 20 мл раствора, содержащего в 1 л 12 г щелочи, израсходовано 24 мл 0,25 н раствора кислоты. Вычислить молярную массу эквивалентов щелочи. (Ответ: 40 г/моль).
5.18. На нейтрализацию 31 мл 0,16 н раствора щелочи требуется 217 мл раствора H2SO4. Чему равны нормальность и титр раствора H2SO4?
(Ответ: 0,023 н; 1,127∙10‾3 г/мл).
5.19. Смешали 10 мл 10 %-ного раствора HNO3 (ρ = 1,056 г/мл) и 100 мл
30 %-ного раствора HNO3 (ρ = 1,184 г/мл). Вычислить массовую долю HNO3 в полученном растворе. (Ответ: 28,36 %).
5.20. Вычислить массовую долю (%) нитрата серебра в 1,4 М растворе, плотность которого 1,18 г/мл. (Ответ: 20,2 %).
Лабораторная работа 6
Источник
