Чем вызвано искривление поверхности жидкости вблизи стенок сосуда

Капиллярные явления

Искривление поверхности жидкости у краев сосуда особенно отчетливо видно в узких трубках, где искривляется вся свободная поверхность жидкости. В трубках с узким сечением эта поверхность представляет собой часть сферы, ее называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 1, а), а у несмачивающей – выпуклый (рис. 1, б). Так как площадь поверхности мениска больше, чем площадь поперечного сечения трубки, то под действием молекулярных сил искривленная поверхность жидкости стремится выпрямиться.

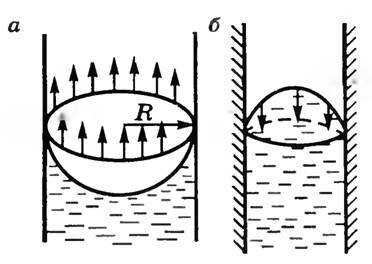
Рис. 1

Силы поверхностного натяжения создают дополнительное (лапласово) давление под искривленной поверхностью жидкости.

Для расчета избыточного давления предположим, что поверхность жидкости имеет форму сферы радиуса R (рис. 2. а), от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса r = R sin α.

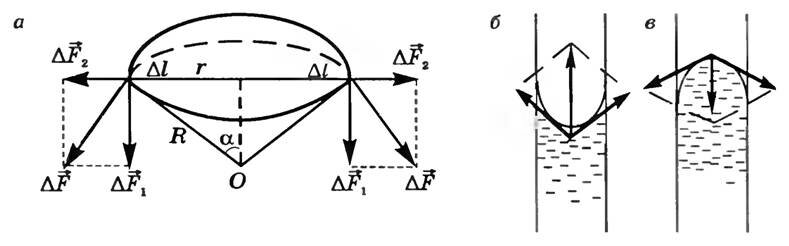
Рис. 2

На каждый бесконечно малый элемент длины Δl этого контура действует касательная к поверхности сферы сила поверхностного натяжения, модуль которой (~Delta F = alpha Delta l). Разложим вектор (~Delta vec F) на две составляющие силы (~Delta vec F_1) и (~Delta vec F_2). Из рисунка 2, а видим, что геометрическая сумма сил (~Delta vec F_2) для двух выделенных диаметрально противоположных элементов Δl равна нулю. Поэтому сила поверхностного натяжения направлена перпендикулярно плоскости сечения внутрь жидкости (рис. 2, в) и модуль ее равен

(~F = sum Delta F_1 = sum Delta F sin alpha = sum alpha Delta l frac rR = frac{alpha r}{R} sum Delta l = frac{alpha r}{R} cdot 2 pi r = frac{2 alpha pi r^2}{R} .)

Избыточное давление, создаваемое этой силой[~p = frac FS], где S = πr2 – площадь основания сферического сегмента. Поэтому

(~p = frac{2 alpha pi r^2}{R cdot pi r^2} = frac{2 alpha}{R} .)

Если поверхность жидкости вогнутая, то сила поверхностного натяжения направлена из жидкости (рис. 2, б) и давление под вогнутой поверхностью жидкости меньше, чем под плоской, на ту же величину (~p = frac{2 alpha}{R}) . Эта формула определяет лапласово давление для случая сферической формы свободной поверхности жидкости. Она является частным случаем формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

(~p = alpha left( frac{1}{R_1} + frac{1}{R_2} right),)

где R1 и R2 – радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости. Для цилиндрической поверхности (R1 = l; R2 = ∞) избыточное давление (~p = frac{alpha}{R}) .

Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие наличия силы лапласова давления жидкость в капилляре поднимается (если жидкость смачивающая) или опускается (если жидкость несмачивающая) (рис. 3, а, б), так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет.

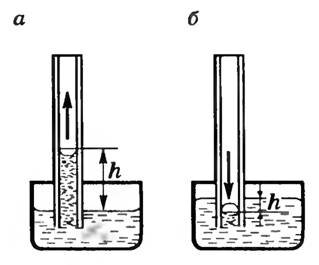
Рис. 3

Явления изменения высоты уровня жидкости в капиллярах по сравнению с уровнем жидкости в широких сосудах называются капиллярными явлениями.

Жидкость в капилляре поднимается или опускается на такую высоту h, при которой сила гидростатического давления столба жидкости уравновешивается силой избыточного давления, т.е.

(~frac{2 alpha}{R} = rho gh .)

Откуда (~h = frac{2 alpha}{rho gR}). Если смачивание не полное θ ≠ 0 (θ ≠ 180°), то, как показывают расчеты, (~h = frac{2 alpha}{rho gR} cos theta).

Капиллярные явления весьма распространены. Поднятие воды в почве, система кровеносных сосудов в легких, корневая система у растений, фитиль и промокательная бумага – капиллярные системы.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. – Мн.: Адукацыя i выхаванне, 2004. – C. 182-184.

Источник

Авторы: А. М. Емельяненко, Н. В. Чураев

КАПИЛЛЯ́РНЫЕ ЯВЛЕ́НИЯ, со­во­куп­ность яв­ле­ний, обу­слов­лен­ных по­верх­но­ст­ным на­тя­же­ни­ем на гра­ни­це раз­де­ла не­сме­ши­ваю­щих­ся сред (в сис­те­мах жид­кость – жид­кость, жид­кость – газ или пар) при на­ли­чии ис­крив­ле­ния по­верх­но­сти. Ча­ст­ный слу­чай по­верх­но­ст­ных яв­ле­ний.

Рис. 1.

При от­сут­ст­вии си­лы тя­же­сти жид­кость ог­ра­ни­чен­ной мас­сы под воз­дей­ст­ви­ем по­верх­но­ст­но­го на­тя­же­ния стре­мит­ся за­нять объ­ём с ми­ним. по­верх­но­стью, т. е. при­ни­ма­ет фор­му ша­ра. В ус­ло­ви­ях дей­ст­вия си­лы тя­же­сти не слиш­ком вяз­кая жид­кость дос­та­точ­ной мас­сы при­ни­ма­ет фор­му со­су­да, в ко­то­рый на­ли­та, и её сво­бод­ная по­верх­ность при от­но­си­тель­но боль­шой пло­ща­ди (вда­ли от сте­нок со­су­да) ста­но­вит­ся пло­ской, т. к. роль по­верх­но­ст­но­го на­тя­же­ния ме­нее су­ще­ст­вен­на, чем си­лы тя­же­сти. При взаи­мо­дей­ст­вии с по­верх­но­стью др. жид­ко­сти или твёр­до­го те­ла (напр., со стен­ка­ми со­су­да) по­верх­ность рас­смат­ри­вае­мой жид­ко­сти ис­крив­ля­ет­ся в за­ви­си­мо­сти от на­ли­чия или от­сут­ст­вия сма­чи­ва­ния. Ес­ли име­ет ме­сто сма­чи­ва­ние, т. е. мо­ле­ку­лы жид­ко­сти 1 (рис. 1) силь­нее взаи­мо­дей­ст­ву­ют с мо­ле­ку­ла­ми по­верх­но­сти 3, чем с мо­ле­ку­ла­ми др. жид­ко­сти (или га­за) 2, то под воз­дей­ст­ви­ем раз­но­сти сил меж­мо­ле­ку­ляр­но­го взаи­мо­дей­ст­вия жид­кость 1 под­ни­ма­ет­ся по стен­ке со­су­да – уча­сток жид­ко­сти, при­мы­каю­щий к стен­ке, ис­крив­ля­ет­ся. Дав­ле­ние, вы­зы­вае­мое подъ­ё­мом жид­ко­сти, урав­но­ве­ши­ва­ет­ся ка­пил­ляр­ным дав­ле­ни­ем $Delta p$ – раз­но­стью дав­ле­ний над и под ис­крив­лён­ной по­верх­но­стью раз­де­ла. Ве­ли­чи­на ка­пил­ляр­но­го дав­ле­ния за­ви­сит от сред­не­го ра­диу­са $r$ кри­виз­ны по­верх­но­сти и оп­ре­де­ля­ет­ся фор­му­лой Ла­п­ла­са: $Delta p=2 sigma/r$, где $sigma$ – по­верх­но­ст­ное на­тя­же­ние. Ес­ли гра­ни­ца раз­де­ла фаз пло­ская ($r= infty$), то в ус­ло­ви­ях ме­ха­нич. рав­но­ве­сия сис­те­мы дав­ле­ния с обе­их сто­рон гра­ни­цы раз­де­ла рав­ны и $Delta p=0$. В слу­чае во­гну­той по­верх­но­сти жид­ко­сти ($r lt 0$) дав­ле­ние в жид­ко­сти ни­же, чем дав­ле­ние в гра­ни­ча­щей с ней фа­зе и $Delta p lt 0$; для вы­пук­лой по­верх­но­сти ($r>0$) $Delta p>0$.

Ес­ли стен­ки со­су­да при­бли­зить друг к дру­гу, зо­ны ис­крив­ле­ния по­верх­но­сти жид­ко­сти об­ра­зу­ют ме­ниск – пол­но­стью ис­крив­лён­ную по­верх­ность. Об­ра­зо­вав­шая­ся сис­те­ма на­зы­ва­ет­ся ка­пил­ля­ром; в нём в ус­ло­ви­ях сма­чи­ва­ния дав­ле­ние под ме­ни­ском по­ни­же­но и жид­кость в ка­пил­ля­ре под­ни­ма­ет­ся (над уров­нем сво­бод­ной по­верх­но­сти жид­ко­сти в со­су­де); вес стол­ба жид­ко­сти вы­со­той $h$ урав­но­ве­ши­ва­ет ка­пил­ляр­ное дав­ле­ние $Delta p$. Не­сма­чи­ваю­щая жид­кость в ка­пил­ля­ре об­ра­зу­ет вы­пук­лый ме­ниск, дав­ле­ние над ко­то­рым вы­ше, и жид­кость в нём опус­ка­ет­ся ни­же уров­ня сво­бод­ной по­верх­но­сти вне ка­пил­ля­ра. Вы­со­та под­ня­тия (опус­ка­ния) жид­ко­сти в ка­пил­ля­ре от­но­си­тель­но сво­бод­ной по­верх­но­сти (где $r= infty$ и $Delta p=0$) оп­ре­де­ля­ет­ся со­от­но­ше­ни­ем: $h=2 sigma cos theta/ Delta rho gr$, где $theta$ – крае­вой угол (угол ме­ж­ду ка­са­тель­ной к по­верх­но­сти ме­ни­ска и стен­кой ка­пил­ля­ра), $Delta rho$ – раз­ность плот­но­стей жид­ко­сти 1 в ка­пил­ля­ре и внеш­ней сре­ды 2, $g$ – ус­ко­ре­ние сво­бод­но­го па­де­ния.

Ис­крив­ле­ние по­верх­но­сти влия­ет на ус­ло­вия рав­но­ве­сия ме­ж­ду жид­ко­стью и её на­сы­щен­ным па­ром: со­глас­но Кель­ви­на урав­не­нию, дав­ле­ние па­ров над ка­п­лей жид­ко­сти по­вы­ша­ет­ся с умень­ше­ни­ем её ра­диу­са, что объ­яс­ня­ет, напр., рост боль­ших ка­пель в об­ла­ках за счёт ма­лых.

Рис. 2.

К ха­рак­тер­ным К. я. от­но­сят­ся ка­пил­ляр­ное впи­ты­ва­ние, по­яв­ле­ние и рас­про­стра­не­ние ка­пил­ляр­ных волн, ка­пил­ляр­ное пе­ре­дви­же­ние жид­ко­сти, ка­пил­ляр­ная кон­ден­са­ция, про­цес­сы ис­па­ре­ния и рас­тво­ре­ния при на­ли­чии ис­крив­лён­ной по­верх­но­сти. Ка­пил­ляр­ное впи­ты­ва­ние ха­рак­те­ри­зу­ет­ся ско­ро­стью, за­ви­ся­щей от ка­пил­ляр­но­го дав­ле­ния и вяз­ко­сти жид­ко­сти. Оно иг­ра­ет су­ще­ст­вен­ную роль в во­до­снаб­же­нии рас­те­ний, дви­же­нии во­ды в поч­вах и др. про­цес­сах, свя­зан­ных с дви­же­ни­ем жид­ко­стей в по­рис­тых сре­дах. Ка­пил­ляр­ная про­пит­ка – один из рас­про­стра­нён­ных про­цес­сов хи­мич. тех­но­ло­гии. В сис­те­мах с не­па­рал­лель­ны­ми стен­ка­ми (или ка­пил­ля­рах ко­нич. се­че­ния) кри­виз­на ме­ни­сков за­ви­сит от рас­по­ло­же­ния в них гра­нич­ных по­верх­но­стей жид­ко­сти, и ка­п­ля сма­чи­ваю­щей жид­ко­сти в них на­чи­на­ет дви­гать­ся к ме­ни­ску с мень­шим ра­диу­сом (рис. 2), т. е. в ту сто­ро­ну, где дав­ле­ние ни­же. При­чи­ной ка­пил­ляр­но­го пе­ре­дви­же­ния жид­ко­сти мо­жет слу­жить и раз­ни­ца сил по­верх­но­ст­но­го на­тя­же­ния в ме­ни­сках, напр. при су­ще­ст­во­ва­нии гра­ди­ен­та темп-ры или при ад­сорб­ции по­верх­но­ст­но-ак­тив­ных ве­ществ, сни­жаю­щих по­верх­но­ст­ное на­тя­же­ние.

Ка­пил­ляр­ной кон­ден­са­ци­ей на­зы­ва­ют про­цесс кон­ден­са­ции па­ра в ка­пил­ля­рах и мик­ро­тре­щи­нах по­рис­тых тел, а так­же в про­ме­жут­ках ме­ж­ду сбли­жен­ны­ми твёр­ды­ми час­ти­ца­ми или те­ла­ми. Не­об­хо­ди­мое ус­ло­вие ка­пил­ляр­ной кон­ден­са­ции – на­ли­чие сма­чи­ва­ния по­верх­но­сти тел (час­тиц) кон­ден­си­рую­щей­ся жид­ко­стью. Про­цес­су ка­пил­ляр­ной кон­ден­са­ции пред­ше­ст­ву­ет ад­сорб­ция мо­ле­кул па­ра по­верх­но­стью тел и об­ра­зо­ва­ние ме­ни­сков жид­ко­сти. В ус­ло­ви­ях сма­чи­ва­ния фор­ма ме­ни­сков во­гну­тая и дав­ле­ние $p$ на­сы­щен­но­го па­ра над ни­ми ни­же, чем дав­ле­ние на­сы­щен­но­го па­ра $p_0$ при тех же ус­ло­ви­ях над пло­ской по­верх­но­стью. Т. е. ка­пил­ляр­ная кон­ден­са­ция про­ис­хо­дит при бо­лее низ­ких, чем $p_0$, дав­ле­ни­ях.

Ис­крив­ле­ние по­верх­но­сти жид­ко­сти мо­жет су­ще­ст­вен­но вли­ять на про­цес­сы ис­па­ре­ния, ки­пе­ния, рас­тво­ре­ния, за­ро­ды­ше­об­ра­зо­ва­ния при кон­ден­са­ции па­ра и кри­стал­ли­за­ции. Так, свой­ст­ва сис­тем, со­дер­жа­щих боль­шое ко­ли­че­ст­во ка­пель или пу­зырь­ков га­за (эмуль­сий, аэ­ро­зо­лей, пен), и их фор­ми­ро­ва­ние во мно­гом оп­ре­де­ля­ют­ся К. я. Они ле­жат так­же в ос­но­ве мн. тех­но­ло­гич. про­цес­сов: фло­та­ции, спе­ка­ния по­рош­ков, вы­тес­не­ния неф­ти из пла­стов вод­ны­ми рас­тво­ра­ми по­верх­но­ст­но-ак­тив­ных ве­ществ, ад­сорб­ци­он­но­го раз­де­ле­ния и очи­ст­ки га­зо­вых и жид­ких сме­сей и т. п.

Впер­вые К. я. бы­ли ис­сле­до­ва­ны Ле­о­нар­до да Вин­чи. Сис­те­ма­тич. на­блю­де­ния и опи­са­ния К. я. в тон­ких труб­ках и ме­ж­ду пло­ски­ми, близ­ко рас­по­ло­жен­ны­ми стек­лян­ны­ми пла­сти­на­ми про­вёл в 1709 Ф. Хокс­би, де­мон­ст­ра­тор Лон­дон­ско­го ко­ро­лев­ско­го об-ва. Ос­но­вы тео­рии К. я. за­ло­же­ны в тру­дах Т. Юн­га, П. Ла­п­ла­са, а их тер­мо­ди­на­мич. рас­смот­ре­ние осу­ще­ст­вил Дж. Гиббс (1876).

Источник

КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ – совокупность явлений, обусловленных действием межфазного поверхностного натяжения на границе раздела несмешивающихся сред; к К. я. обычно относят явления в жидкостях, вызванные искривлением их поверхности, граничащей с др. жидкостью, газом или собств. паром. К. я.- частный случай поверхностных явлений. В отсутствие силы тяжести поверхность жидкости искривлена всегда. Под воздействием поверхностного натяжения ограниченный объём жидкости стремится принять форму шара, т. е. занять объём с мин. поверхностью. Силы тяжести существенно меняют картину. Жидкость с относительно малой вязкостью быстро принимает форму сосуда, в к-рый налита, причём её свободная поверхность (не граничащая со стенками сосуда) в случае достаточно больших масс жидкости и большой площади свободной поверхности практически плоская. Однако по мере уменьшения массы жидкости роль поверхностного натяжения становится более существенной, чем сила тяжести. Так, напр., при дроблении жидкости в газе (или газа в жидкости) образуются капли (пузырьки) сферич. формы. Свойства систем, содержащих большое кол-во капель или пузырьков (эмульсии, жидкие аэрозоли, пены), и условия их формирования во многом определяются кривизной поверхности этих образований, то есть К. я. Большую роль К. я. играют и в зародышеобразовании при конденсации пара, кипении жидкостей, кристаллизации. Искривление поверхности жидкости может происходить также в результате её взаимодействия с поверхностью др. жидкости или твёрдого тела. В этом случае существенно наличие или отсутствие смачивания жидкостью этой поверхности. Если имеет место смачивание, т. е. молекулы жидкости 1 (рис. 1) сильнее взаимодействуют с поверхностью твёрдого тела 3, чем с молекулами др. жидкости (или газа) 2, то под воздействием разности сил межмолекулярного взаимодействия жидкость поднимается по стенке сосуда и примыкающий к твёрдому телу участок поверхности жидкости будет искривлён. Гидростатич. давление, вызванное подъёмом уровня жидкости, уравновешивается капиллярным давлением – разностью давлений над и под искривлённой поверхностью, величина к-рого связана с локальной кривизной поверхности жидкости. Если сближать плоские стенки сосуда с жидкостью, то зоны искривления перекроются и образуется мениск – полностью искривлённая поверхность. В таком капилляре в условиях смачивания под вогнутым мениском давление понижено, жидкость поднимается; вес столба жидкости вые. h0 уравновешивает капиллярное давление Dр. В условиях равновесия

где r1 и r2 – плотности жидкости 1 и газа 2, s12 – межфазное поверхностное натяжение, g-ускорение свободного падения, r-радиус средней кривизны поверхности мениска (1/r=1/R1+1/R2, где R1 и R2 – радиусы кривизны мениска в двух взаимно перпендикулярных плоскостях сечения). Для смачивающей жидкости r<0 и h0>0. Несмачивающая жидкость образует выпуклый мениск, капиллярное давление под к-рым положительно, что приводит к опусканию жидкости в капилляре ниже уровня свободной поверхности жидкости (h0<0). Радиус кривизны r связан с радиусом капилляра rк соотношением r=-rк/cosq, где q – краевой угол, образуемый поверхностью жидкости со стенками капилляра. Из ур-ния (1) можно получить т. н. капиллярную постоянную а – величину, характеризующую размеры системы L<а, при к-рых становятся существенными К. я.: Для воды при темп-ре 20 °С а=0,38 см. К К. я. относятся капиллярное впитывание, появление и распространение капиллярных волн, капиллярное передвижение жидкости, капиллярная конденсация, процессы испарения и растворения при наличии искривлённой поверхности. Для капиллярного впитывания важной характеристикой является его скорость v, определяемая величиной капиллярного давления и вязким сопротивлением течению жидкости в капилляре. Скорость v изменяется со временем впитывания t, и для вертикально расположенного капилляра

где h(t) – положение мениска в момент времени t (рис. 1), h – коэф. вязкости жидкости. При впитывании в горизонтальный капилляр

При v>10-3 см/с следует учитывать возможную зависимость краевого угла q от v, а в нек-рых случаях – вязкое сопротивление вытесняемого из капилляра газа (или др. жидкости). Скорость капиллярного впитывания играет существ, роль в водоснабжении растений, движении жидкости в почвах и др. пористых телах. Капиллярная пропитка – один из распространённых процессов хим. технологии. Искривление свободной поверхности жидкости под действием внеш. сил (напр., ветра, вибрации) вызывает появление и распространение капиллярных волн (“ряби” на поверхности жидкости). Самопроизвольное образование поверхностных волн – флуктуации толщины тонких слоев жидкости (струи, плёнки) – является причиной их неустойчивости по отношению к состоянию капель или капиллярного конденсата. Разность капиллярного давления, возникающая в результате разл. кривизны поверхностей менисков, может вызывать капиллярное передвижение жидкости (рис. 2).

Для смачивающих жидкостей поток жидкости направлен к мениску с меньшим радиусом кривизны (т. е. в сторону меньшего давления). Причиной капиллярного передвижения может быть не только градиент кривизны, но и градиент поверхностного натяжения жидкости Так, градиент темп-ры приводит к разности поверхностного натяжения и, следовательно, к разности капиллярного давления в жидкости (термокапиллярное течение). Этим же объясняется движение капель жидкости и пузырьков газа в неравномерно нагретой среде: под влиянием градиента поверхностного натяжения приходит в движение поверхность пузырьков или капель. Аналогичный эффект наблюдается и при изменении s12 при адсорбции поверхностно-активных веществ (ПАВ): ПАВ снижают s12 и жидкость перемещается в том направлении, где адсорбция ПАВ на поверхности жидкости меньше (эффект Марангони – Гиббса). Искривление поверхности раздела фаз приводит к изменению величины равновесного давления пара р над ней или растворимости твёрдых тел. Так, напр., над каплями жидкости р выше, чем давление насыщ. пара ps над плоской поверхностью жидкости при той же темп-ре Т. Соответственно растворимость с мелких частиц в окружающей среде выше, чем растворимость cs плоской поверхности того же вещества. Эти изменения описываются Кельвина уравнением ,полученным из условия равенства хим. потенциалов в смежных фазах в состоянии термодинамич. равновесия:

где V – молярный объём жидкости или твёрдого тела. Для шарообразных частиц г по абс. величиче равно их радиусу. Понижение или повышение р и с зависит, в соответствии с (4), от знака r (r>0 для выпуклых, и r<0 для вогнутых поверхностей). Так, в отличие от рассмотренного выше случая давление пара в пузырьке или над поверхностью вогнутого мениска понижено: p<ps.

Ур-ние (4) определяет направление переноса вещества (от больших значений р и с к меньшим) в процессе перехода системы к состоянию термодинамич. равновесия. Это приводит, в частности, к тому, что крупные капельки (или частицы) растут за счёт испарения (растворения) более мелких, а неровные поверхности (при условии постоянства межфазного натяжения) сглаживаются за счёт испарения (растворения) выступов и заполнения впадин. Заметные отличия давления и растворимости имеют место лишь при достаточно малых r (для воды, напр., при |r|[0,1 мкм). Поэтому ур-ние Кельвина часто используется для характеристики состояния малых объектов (коллоидные системы, тонкопористые тела, зародыши новой фазы). Капиллярная конденсация – процесс перехода пара в жидкость, заполняющую капилляры, щели или промежутки между частицами, с образованием вогнутых капиллярных менисков. Необходимое условие капиллярной конденсации – смачивание жидкостью поверхности конденсации, ей предшествует адсорбция молекул пара на поверхности. Степень заполнения капилляров или пористых тел капиллярно-конденсированной жидкостью описывается ур-нием Кельвина (подробнее см. в ст. Капиллярная конденсация ).Отрицат. капиллярное давление (Dр<0) может удерживать смачиваемые жидкостью частицы (рис. 3). Если яастицы дисперсного тела не связаны прочно, возможна его объёмная деформация под действием капиллярных сил – капиллярная контракция. Так, напр., рост капиллярного давления при высушивании может приводить к значит, усадке материалов. К. я. впервые были открыты и исследованы Леонардо да Винчи (Leonardo da Vinci), Б. Паскалем (В. Pascal) и Дж. Жюреном (J. Jurin) в опытах с капиллярными трубками. Теория К. я. развита в работах П. С. Лапласа (P. S. Laplace), Т. Юнга (Th. Young), И. С. Громеки и Дж. У. Гиббса (J. W. Gibbs). Лит.: Громека И. С., Собр. соч., М., 1952; Адамсон А., Физическая химия поверхностей, пер. с англ., М., 1979; Современная теория капиллярности, под ред. А. И. Русанова, Ф. Ч. Гудрича, Л., 1980; Дерягин Б. В., Чураев Н. В., Смачивающие пленки, М., 1984; Роулинсон Д ж., Уидом Б., Молекулярная теория капиллярности, пер. с англ., М., 1986. Н. В. Чураев.

Предметный указатель >>

Источник