Число циклов нагружения сосуда это
52857.6- 2007 |
2008 |
27 2002 . 184- , – 1.0-2004 .
1 – ( ); ( ); – – ( ); , ()
2 260
3 27 2007 . 503-
4 : 97/23 29 1997 . -, , ; 13445-3:2002 , . 3. (EN 13445-3:2002 Unfired pressure vessel – Part 3: De)
5
, – . () . , –
Vessels and apparatus. Norms and methods of strength calculation.
Strength calculation under low-cyclic loads
– 2008-04-01
, , , , 106 .
, , . , , 380 , 420 – , 520 – , 150 – , 250 – , 300 – .
52857.1, 52857.2, 52857.3, 52857.9, 52857.11.
:
52857.1-2007 . .
52857.2-2007 . . ,
52857.3-2007 . . .
52857.4-2007 . .
52857.5-2007 . .
52857.7-2007 . .
52857.9-2007 . .
52857.11-2007 . . ,
30780-2002 . .
– – , 1 , , . (), () . , , , , .
:
– , ;
– , ;
– , ;
t – , ;
D – , ;
t – , ;
[F] – , ;
ΔFj – , ;
i – ;
j – ( );
i – i- (, , . );
ΔHi – i- ( );
σ – ;
[] – , ͷ;
ΔMj – , ͷ;
Nj – j- ;
[Nj] – j- ;
N – ;
[N] – ;
nN – ;
σ – ;
– , ;
[] – , ;
Δpj – , ;
s – , ;
q – ;
Rm/t – , ;
Δj – , ;
Δαj – , ;
t – , ;
U – ;
α; α1; α2 – , 1/;
δ – , ;
η – , ;
ξ – , ;
σ – , ;
[σ] – , ;
Δσ; Δσ; Δσz; Δτxy; Δτxz; Δτyz – , ;
Δσ1; Δσ2; Δσ3 – , .
4.1 , .
4.2 .
4.3 , .
4.4 .
Δpj = max (j; 0) – min (j; 0);
ΔFj = max (Fj; 0) – min (Fj; 0);
ΔMj = max (Mj; 0) – min (Mj; 0).
. ( 1) ( 2) (. 1).
1 , .
1
4.5 :
– , ;
– ;
– ;
– , .
4.6 :
– ;
– , ;
– , 15 % . , 10 % ;
– , 15 . , (D – , s – ).
4.7 .
4.8 .
5.1 . – , . .
5.2 6 7 , :
– :
103 – , 59-1, 63, 2 3, 1-0, 1-00, 4-0, 3;
3103 – 2, 3, 3 ;
0,2103 – 59-1-1, 62-1 5 6;
106 – -85, -8, 00, 0, 1;
– 4.6;
– .
5.3 5.2 , , 6 7.
, 6 .
6.1 , , , .
σa ≤ [σa]. (1)
8.
6.2 , .
N ≤ [N]. (2)
8.
6.3 Nj , :
(3)
j- 8 j- .
6.4 j-
(4)
ξ η 1 2. ξ .
[F] [M] 52857.2 52857.3.
1
2
η | ||
1,5 | ||
2,0 | ||
( ) | , | |
(Rm < 540 ) | ||
2,5 | ||
max {1,5; 3,0-} | ||
3,0 | ||
, | , , | |
3,0 | ||
(Rm < 540 ) | ||
4,0 | ||
(Rm > 540 ) | ||
( ) | ||
( ) | 5,0 |
7.1 – , , .
. Δσ; Δσ; Δσz; Δτxy; Δτxz; Δτyz Δσ1; Δσ2; Δσ3.
52857.4, 52857.5, 52857.7, 52857.9, 52857.11, 30780.
.
(5)
(6)
(7)
Δσ1 Δσ2 (Δσ3 = 0)
(8)
(9)
7.2 σ
σ = 1+q(ασ – 1), (10)
0 ≤ q ≤ 1 – ;
ασ – .
q ασ .
(11)
ξ 1.
φ – 52857.1.
7.3 (1), (13) (2).
, [Nj] (3).
8.1 , 2 – 7,
(12)
8.2 , 2 – 7,
(13)
(14)
, .
2 –
( = 0,6105 , = 150 , = 380 )
3 –
( = 0,45105 , = 170 , = 420 )
4 –
( = 0,6105 , = 170 , = 525 )
5 – (Rm ≥ 700 )
( = 0,25105 , = 280 , = 350 )
1 – , 2, 3 = 0,18105 , = 34 , = 150 ;
2 – 5, 6 = 0,86105 , = 84 , = 150
6 –
1 – 2, 3, 3 = 0,39105 , = 76,5 , = 250 ;
2 – 59-1-1, 63, 62-1, = 0,3105 , = 108,8 , = 250
7 –
1 – 1-0, 1-00 = 0,46105 , = 45,2 , = 300 ;
2 – 4-0 = 0,33105 , = 58,8 , = 400
8 –
9 – 3
( – 0,31105 , = 133,6 , = 350 )
8.3 , t 3.
3
, | , | ct,c | |
0,6105 | 0,4 Rm/t | ||
0,45105 | 0,4 Rm/t | ||
0,6105 | 0,4 Rm/t | ||
Rm > 700 | 0,25105 | 0,4 Rm/t | |
; 2; 3 | 0,18105 | 0,4 Rm/t | |
5; 6 | 0,086105 | 0,4 Rm/t | |
2; 3; 3 | 0,39105 | 0,5 Rm/t | |
59-1; 63; 62-1; | 0,3105 | 0,4 Rm/t | |
1-0; 1-00 | 0,46105 | 0,4 Rm/t | |
4-0 | 0,33105 | 0,4 Rm/t | |
3 | 0,31105 | 0,4 Rm/t |
8.4 :
– nN = 10; nσ = 2,0;
– , nN = 20; nσ = 2,0;
– nN = 30; nσ = 2,5.
8.5 , [σ] [N].
: , ,
Источник
25859-83
( 3648-82)
Steel vessels and apparatuses. Norms and methods of fatigue strength calculation under low-cyclic loads | 25859-83 ( 3648-82) |
11 1983 . 3046
01.07.84
, , 24306-80, , 103 5 . 105 .
14249-80.
3648-82.
1.
1.1. , , , . . , 14249-80 ( ).
, , 380 , 420 525 .
1.2. , – .
1.3. , – .
2.
2.1. , .
2.2. .
2.3. :
1) , ;
2) ;
3) – ;
4) , .
2.4. :
) ;
) , ;
) , 15 % , 25 % , . – . , 10 % ;
) , , 15 20 . , , D – , s – .
) , 50 .
( , . 1).
2.5. .
2.6. . 10 .
3.
3.1. , .
3.2. . 4 5 , :
1) , , . 2.4;
2) ;
3)
Np < [Np] (1)
. [Np] . 1-3.
(1) ξ η [σ] []. ξ η [σ] [].
3.3. (1) , , . 4 5.
, .
. 1
. = 60 . 103 , = 150 , t = 380 .
. 2
. = 45 . 103 , = 230 , t = 420 .
. 3
. = 60 . 103 , = 270 , t = 525 C
4.
4.1.
. (2)
j- . 6 j- .
4.2. j- :
, (3)
ξ η . 1 2. , .
[] [F] 14249-80, 24757-81 25221-82.
1
, | ξ | |
. . | 1,0 | |
. – . . | 1,2 | |
. . . . . | 1,5 |
. ξ , .
( , . 1).
5.
5.1. , , : . .
1.
5.2. (. 4), , ( ) .
5.3. Δσ, Δσy, Δσz, Δτy, Δτz, Δτyz, Δσ1, Δσ2, Δσ3 , .
2
η | |||
. , | 1,5 | ||
. ( ), . | . , . |
| 2,0 |
. | . | ||
. | . | 3,0 | |
, . | , , . | ||
. | . | 3,0 | |
. | . | ||
. | . | ||
. | . | ||
(σ< 540 ) | |||
. | 4,0 | ||
. | . | ||
(σ > 540 ) | |||
. | 4,0 | ||
( ), | |||
( ), | 5,0 |
( , . 1).
. 4
(4)
; (5)
Δσ1 Δσ2
. (6)
5.4. σ
Kσ = 1 + q(ασ – 1), (7)
0 < q < 1 – ;
ασ – .
q ασ .
Kσ = ρξ / φ, (8)
φ – 14249-89;
ξ – . 1.
ρ = 1,0 ;
ρ = 1,1 .
5.5. σA (11) [Nj].
5.6. Nj [Nj] U, (2).
6.
6.1. (9) . 5-8
. (9)
6.2. (10) . 5-8
, (10)
. (11)
, 380
. 5
420
. 6
525
. 7
8
( , . 1).
6.3. . 3.
3
B | ||
0,6 . 105 | 1,43 σ0 – 0,43 σ20 0,66 σ20 – 0,43 σ20 | |
0,45 . 105 | ||
– | 0,6 . 105 | σ0 270 |
( , . 1).
6.4. nN = 10, nσ=2.
6.5. , [σ] [N].
( , . 1).
1
. ( ) . , (, ).
, ( ), .
1.
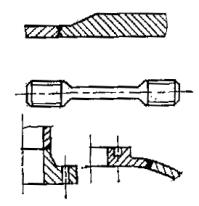
1.1. , , (. 1), :
)
i = 1; 2;
a11 = f1 + εδ3f2; a= – (1- εδ4);
1
1 | 7 | ||
2 | 8 | ||
3 | 9 | ||
4 | 10 | ||
5 |
| 11 | |
6 | 12 |
Δ = a11 a22 – a2;
b1 = -u1 + εδ2u2 + f1q01 + εδ3f2q02;
b2 = υ1 + εδ2υ 2 – q01 + εδ4q02;
fi, ui, υi q0i (i = l; 2) . 2.
2
( 1:2) | ||||
fi | 1 | |||
ui | 2 – μ 2 | 2 – μ 2 cosβi | 1 – μ 2sinΘi | 1 – μ – 3sin2Θi 2sinΘi |
υi | 3sinβi 2 νρ1cos2βi | |||
q 0i | + νρ1tg βi | + νρ1ctg Θi | + νρ1ctg Θi | |
. + q01 (. 1 );
( , . 1).
) Q0i 0 (. 1 ;
;
)
;
,
η = ηφ = 1 – ;
– ;
– ;
– .
+ .
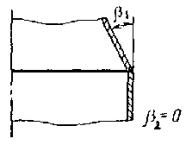
1.2. , (. 2), :
)
;
; (i = 1; 2)
;
;
;
;
;
;
. 1.1, .
) Qi Mi
. 1
. 2
)
;
.
ηx ηφ . 1.1.
l.3. , (. 3), :
. 3
)
;
;
.
u2, f2, n2 q02 . 2 ;
) Q0 M0
;
)
;
.
η ηφ . 1.1, .
:
1)
Θi > 15;
2) – , ;
– ;
3) ,
h b – (. 2).
, , (. 3).
1.4. ( 4).
( Θ = Θ0)
.
.
.
( , . 1).
3
( , . 1).
.
. 4
(λi)
.
λi
.
R2 = 0,5(D + s2),
r0 – ;
Δ1, Δ2 – , .
.
2.
2.1. , (, ),
)
a11 = f1 + εδ3f2;
a12 = -(1 – εδ4); ;
;
) Q0 M0
)
;
.
+ . , (i = 1; 2) fi . 2.
. 1, 2 α1, α2 , . , . 5 .
2.2. :
)
;
;
;
;
*
_____________
14249-80.
1 – ; 2 – .
. 5
) Qi Mi (i = 1; 2)
) (i= 1, 2)
. 1.3 .
2
, (/2) | |
A11, A12, 22, * , 11, a12, 22 | |
, (/2) | |
, () | b |
B1, B2, b, b1, b2 * | |
, () | |
, () | D |
(/2) | , 1, E2, |
, 2 (2) | F |
, () | [F] |
, () | ΔFj |
fi (i = 1, 2) | |
j- (, , . ) | Hj |
ΔHj | |
, () | h |
, () | h0, hi (i = 1, 2) |
, () | h |
, 4 (4) | I |
i | |
( ) | j |
Kσ | |
, () | L |
, () | l1, l2 |
, / ( /) | M0, Mi (i = 1, 2) |
, ( ) | [M] |
, ( ) | ΔMj |
N1 | |
[Nj] | |
Np | |
[Np] | |
nN | |
nσ | |
, (/2); , > 0, , (), < 0 | |
, (/2) | [] |
. (/2) | Δpj |
, / (/) | Q0, Q0i, Qi (i = 1, 2) |
q | |
q0 | |
q0i (i = 1, 2) | |
, () | R |
, () | R0 |
, () | R1, R2 |
, () | r0 |
, () | s0 |
, () | si (i = 1, 2) |
, | ΔTTj |
, | ΔTαj |
, | t, t,t i (i = 1, 2) |
U | |
ui (i = 1, 2) | |
, 1/ | a, a1, a2 |
, … | β, βi(i = 1, 2) |
ν | |
Δ δ | |
ε, ε | |
, | η |
ηi (i = 1, 2) | |
η, ηφ | |
, …. | Θ, Θ0, Θi (i = 1, 2) |
υi (i = 1, 2) | |
, | λi (i = 1, 2) |
μ | |
, | ξ |
ρ, ρi (i = 1, 2) | |
, , (/2) | σ |
20 , (/2) | σ20 |
20 , (/2) | σ20 |
106 , (/2) | σ0 |
, (/2) | σ, σi (i = 1, 2) |
, (/2) | σφ, σφi (i = 1, 2) |
, (/2) | [σ] |
, (/2) | [σA] |
, (/2) | Δσ Δτ |
1, 2 |
Источник
25859-83 ( 3648-82)
11 1983 . 3046 01.07.84 , , 24306-80, , 103 5 . 105 . 14249-80. 3648-82. 1.1. , , , . . , 14249-80 ( ). , , 380 , 420 525 . 1.2. , – . 1.3. , – . 2.1. , . 2.2. . 2.3. : 1) , ; 2) ; 3) – ; 4) , . 2.4. : ) ; ) , ; ) , 15 % , 25 % , . – . , 10 % ; ) , , 15 20 . , , D – , s – . ) , 50 . ( , . 1). 2.5. . 2.6. . 10 . 3.1. , . 3.2. . 4 5 , : 1) , , . 2.4; 2) ; 3) Np < [Np] (1) . [Np] . 1-3. (1) ξ η [σ] []. ξ η [σ] []. 3.3. (1) , , . 4 5. , . . 1 . = 60 . 103 , = 150 , t = 380 . . 2 . = 45 . 103 , = 230 , t = 420 . . 3 . = 60 . 103 , = 270 , t = 525 C 4.1. . (2) j- . 6 j- . 4.2. j- : , (3) ξ η . 1 2. , . [] [F] 14249-80, 24757-81 25221-82. 1
. ξ , . ( , . 1). 5.1. , , : . . 1. 5.2. (. 4), , ( ) . 5.3. Δσ, Δσy, Δσz, Δτy, Δτz, Δτyz, Δσ1, Δσ2, Δσ3 , . 2
( , . 1). . 4 (4) ; (5) Δσ1 Δσ2 . (6) 5.4. σ Kσ = 1 + q(ασ – 1), (7) 0 < q < 1 – ; ασ – . q ασ . Kσ = ρξ / φ, (8) φ – 14249-89; ξ – . 1. ρ = 1,0 ; ρ = 1,1 . 5.5. σA (11) [Nj]. 5.6. Nj [Nj] U, (2). 6.1. (9) . 5-8 . (9) 6.2. (10) . 5-8 , (10) . (11) , 380 . 5 420 . 6 525 . 7 8 ( , . 1). 6.3. . 3. 3
( , . 1). 6.4. nN = 10, nσ=2. 6.5. , [σ] [N]. ( , . 1). . ( ) . , (, ). , ( ), . 1. 1.1. , , (. 1), : ) i = 1; 2; a11 = f1 + εδ3f2; a= – (1- εδ4); 1
Δ = a11 a22 – a2; b1 = -u1 + εδ2u2 + f1q01 + εδ3f2q02; b2 = υ1 + εδ2υ 2 – q01 + εδ4q02; fi, ui, υi q0i (i = l; 2) . 2. 2
. + q01 (. 1 ); ( , . 1). ) Q0i 0 (. 1 ; ; ) ; , η = ηφ = 1 – ; – ; – ; – . + . 1.2. , (. 2), : ) ; ; (i = 1; 2) ; ; ; ; ; ; . 1.1, . ) Qi Mi . 1 . 2 ) ; . ηx ηφ . 1.1. l.3. , (. 3), : . 3 ) ; ; . u2, f2, n2 q02 . 2 ; ) Q0 M0 ; ) ; . η ηφ . 1.1, . : 1) Θi > 15; 2) – , ; – ; 3) , h b – (. 2). , , (. 3). 1.4. ( 4). ( Θ = Θ0) . . . ( , . 1). 3 ( , . 1). . . 4 (λi) . λi . R2 = 0,5(D + s2), r0 – ; Δ1, Δ2 – , . . 2. 2.1. , (, ), ) a11 = f1 + εδ3f2; a12 = -(1 – εδ4); ; ; ) Q0 M0 ) ; . + . , (i = 1; 2) fi . 2. . 1, 2 α1, α2 , . , . 5 . 2.2. : ) ; ; ; ; * _____________ 14249-80. 1 – ; 2 – . . 5 ) Qi Mi (i = 1; 2) ) (i= 1, 2) . 1.3 .
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Источник