Число молекул идеального газа в некотором сосуде равно n
Число молекул идеального газа в некотором сосуде равно N. Внутренней энергией этого газа будет суммарная кинетическая …
Предмет: Физика (22231 вопросов)
Помог сайт? Помоги другу:
- энергия молекул одного моля этого газа
- и потенциальная энергия всех N молекул в этом сосуде
- и потенциальная энергия молекул одного моля этого газа
- энергия всех N молекул газа в этом сосуде
Тип вопроса: Вопрос с одним правильными вариантом
Вопрос задал(а): Анонимный пользователь, 13 Ноябрь 2020 в 19:35
На вопрос ответил(а): Анастасия Степанова, 13 Ноябрь 2020 в 19:35
Похожие вопросы
Число молекул идеального газа в некотором сосуде равно N. Внутренней энергией этого газа будет суммарная кинетическая …
и потенциальная энергия молекул одного моля этого газа
энергия молекул одного моля этого газа
и потенциальная энергия всех N молекул в этом сосуде
энергия всех N молекул газа в этом сосуде
В сосуде, разделенном на равные части неподвижной непроницаемой перегородкой находится газ. Температуры газа в каждой части сосуда равны, по массе газа в левой части больше, чем в правой М1>М2.
Функция распределения скоростей молекул газа в сосуде будет описываться кривыми…
Как изменится средняя кинетическая энергия молекул идеального одноатомного газа при увеличении его абсолютной температуры в 2 раза? Объем газа не изменяется.
уменьшится в 2 раза
не изменится
увеличится в раза
увеличится в 2 раза
Как изменится средняя кинетическая энергия молекул идеального одноатомного газа при увеличении его абсолютной температуры в 2 раза? Объем газа не изменяется.
уменьшится в 2 раза
не изменится
увеличится в раза
увеличится в 2 раза
Источник
Пусть в некотором сосуде заключен газ. Молекулы, двигаясь хаотично, сталкиваются со стенками сосуда и производят давление. Это явление определяется числом ударов, производимых молекулами за единицу времени на единицу площади поверхности сосуда.
Сила ударов молекулы, а, следовательно, и давление молекулы зависит от скорости и массы молекул. Но от скорости и массы молекул зависит кинетическая энергия, следовательно, имеется возможность выразить давление газа на стенки сосуда через кинетическую энергию молекул и их число.
Вычисления показывают, что давление газа будет
P=(2/3)nWk
где n – число молекул в единице объема. Это уравнение называют основным уравнением кинетической теории газов. Таким образом, среднюю кинетическую энергию молекул газа можно найти:
Wk=(m0ν2KB)/2, Wk=kT3/2, Wk=(3p)/(2n)
Внутренняя энергия идеального газа
Внутренняя энергия идеального одноатомного газа легко вычисляется. Вспомним, что молекулы идеального газа не взаимодействуют из-за наличия больших межмолекулярных промежутков и, как условились ранее, энергия взаимодействия равна нулю. Значит, внутренняя энергия идеального газа определяется только кинетической энергией движения молекул
U=ΣWk=NWk
где N – число всех молекул газа, а Wk – средняя кинетическая энергия одной молекулы. Вычислим внутреннюю энергию идеального газа, учитывая, что где m – масса всего газа, νкв – средняя скорость молекул. Теперь учтём, что
Wk =kТЗ/2,
тогда U=N(3/2)kT=(3/2)(m/M)NAkT, где m/М – число киломолей,
NA – число Авогадро Произведение NAk заменим одной постоянной величиной R, которую называют универсальной газовой постоянной, т.е. R=NAk. Учитывая это обозначение
U=(3m/2M)RT,
Причём R=6,023×1026 1/кмоль×1,38-23Дж/К=8,314×103Дж/кмольК
Существует ещё один путь вычисления внутренней энергии, через основное уравнение кинетической энергии
U=3p/2n=(3/2)p(n/N)=(3/2)pN
Таким образом, мы проследили возможные пути вычисления внутренней энергии идеального газа.
Уравнение Клапейрона – Менделеева
Состояние любого газа характеризуется его массой,давлением, объемом итемпературой.При изменении одного из параметров изменяются и другие параметры, значит, между ними существует определенная связь, которую легко установить. Вспомним, что внутреннюю энергию газа можно находить
U=(3/2)pV и ν=(3/2)(m/M)RT.
Так как речь идет о внутренней энергии одного и того же газа, то рV/2 = 3RTm/2M =>pV=RTm/M, полученное уравнение называют уравнением Клапейрона – Менделеева. Произведение давления и объема газа равняется произведению числа киломолей, универсальной газовой постоянной и абсолютной температуры.
Нетрудно заметить, что уравнение Клапейрона – Менделеева отражает закон сохранения энергии для идеального газа.
Частные случаи уравнения Клапейрона – Менделеева
Если в уравнении Клапейрона – Менделеева принимать некоторые из параметров постоянными, то получим ряд частных уравнений:
1 m=CONST, pV=RTm/M=>pV/T=CONST
Это уравнение часто называют уравнением состояния идеального газа или объединенным газовым законом. Его часто записывают в следующей форме
2 Допустим, что m=CONST и T=CONST
Такие процессы называют изотермическими. Учитывая это, нетрудно заметить, что в уравнении pV=RTm/M, правая часть будет постоянной при любых изменениях давления и объема pV=CONST или же p1V1= p2V2 .При постоянной массе и температуре объём газа обратно пропорционален давлению закон Бойля-Мариотта.
В координатах p, V процесс изображается гиперболой. Рисунок 10
3 m=CONST и V= CONST. Процесс с постоянным объемом называют изохорическим.
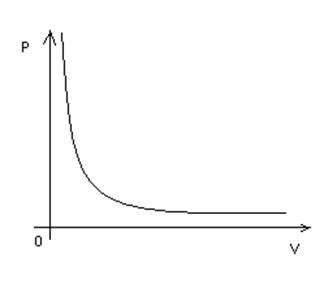
Рисунок 10 – изотермический процесс
Используя уравнение Клапейрона – Менделеева, установим, что:
pV=RTm/M => p/T×m/M×RV, то есть p/T=CONST
Или же р1/Т1=р2Т2 . При изохорическом процессе давление идеального газа прямо пропорционально его абсолютной температуре. Эта связь была открыта французским физиком Шарлем и называется закон Шарля. График процесса изображен на рисунке 11.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Источник
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 7196
$N$ атомов газообразного гелия находятся при комнатной температуре в кубическом сосуде, объем которого равен $1,0 см^{3}$. Найти:
а) вероятность того, что все атомы соберутся в одной половине сосуда;
б) примерное числовое значение $N$, при котором это событие можно ожидать на протяжении времени $t approx 10^{10}$ лет (возраст Вселенной).
Подробнее
Задача по физике – 7197
Найти статистический вес наиболее вероятного распределения $N = 10$ одинаковых молекул по двум одинаковым половинам сосуда. Определить также вероятность такого распределения?
Подробнее
Задача по физике – 7198
$N$ молекул идеального газа находятся в некотором сосуде. Разделим мысленно сосуд на две одинаковые половины А и В. Найти вероятность того, что в половине А сосуда окажется $n$ молекул. Рассмотреть случаи, когда $N = 5$ и $n = 0, 1, 2, 3, 4, 5$.
Подробнее
Задача по физике – 7199
В сосуде объемом $V_{0}$ находится $N$ молекул идеального газа. Найти вероятность того, что в некоторой выделенной части этого сосуда, имеющей объем $V$, окажется $n$ молекул. Рассмотреть, в частности, случай $V = V_{0}/2$.
Подробнее
Задача по физике – 7200
Идеальный газ находится при нормальных условиях. Найти диаметр сферы, в объеме которой относительная флуктуация числа молекул $eta = 1,0 cdot 10^{-3}$. Каково среднее число молекул внутри такой сферы?
Подробнее
Задача по физике – 7201
Один моль идеального газа, состоящего из одноатомных молекул, находится в сосуде при температуре $T_{0} = 300 К$. Как и во сколько раз изменится статистический вес этой системы (газа), если ее нагреть изохорически на $Delta T = 1,0 К$?
Подробнее
Задача по физике – 7202
Найти капиллярное давление:
а) в капельках ртути диаметра $d = 1,5 мкм$;
б) внутри мыльного пузырька диаметра $d = 3,0 мм$, если поверхностное натяжение мыльной воды $alpha = 45 мН/м$.
Подробнее
Задача по физике – 7203
В дне сосуда со ртутью имеется круглое отверстие диаметра $d = 70 мкм$. При какой максимальной толщине слоя ртути она еще не будет вытекать через это отверстие?
Подробнее
Задача по физике – 7204
В сосуде с воздухом при давлении $p_{0}$ находится мыльный пузырек диаметра $d$. Давление воздуха изотермически уменьшили в $n$ раз, в результате чего диаметр пузырька увеличился в $eta$ раз. Найти поверхностное натяжение мыльной воды.
Подробнее
Задача по физике – 7205
Найти давление в пузырьке воздуха диаметра $d = 4,0 мкм$, который находится в воде на глубине $h = 5,0 м$. Атмосферное давление $p_{0}$ нормальное.
Подробнее
Задача по физике – 7206
На дне пруда выделился пузырек газа диаметра $d = 4,0 мкм$. При поднятии этого пузырька к поверхности воды его диаметр увеличился в $n = 1,1$ раза. Найти глубину пруда, в данном месте. Атмосферное давление нормальное, процесс расши рения газа считать изотермическим.
Подробнее
Задача по физике – 7207
Найти разность уровней ртути в двух сообщающихся вертикальных капиллярах, диаметры которых $d_{1} = 0,50 мм$ и $d_{2} = 1,00 мм$, если краевой угол $theta = 138^{ circ}$.
Подробнее
Задача по физике – 7208
Вертикальный капилляр с внутренним диаметром 0,50 мм погрузили в воду так, что длина выступающей над поверхностью воды части капилляра оказалась $h = 25 мм$. Найти радиус кривизны мениска.
Подробнее
Задача по физике – 7209
Стеклянный капилляр длины $l = 110 мм$ с диаметром внутреннего канала $d = 20 мкм$ опустили в вертикальном положении в воду. Верхний конец капилляра запаян. Наружное давление воздуха нормальное. Какая длина $x$ капилляра должна быть погружена в воду, чтобы уровень воды в капилляре совпадал с поверхностью воды вне его?
Подробнее
Задача по физике – 7210
Вертикальный капилляр длины $l$ с запаянным верхним концом привели в соприкосновение с поверхностью жидкости, после чего она поднялась в нем на высоту $h$. Плотность жидкости $rho$, диаметр сечения внутреннего канала капилляра $d$, краевой угол $theta$, атмосферное давление $p_{0}$. Найти поверхностное натяжение жидкости.
Подробнее
Источник
Главная Онлайн учебники База репетиторов России Тренажеры по физике Подготовка к ЕГЭ 2017 онлайн
Глава 3. Молекулярная физика и термодинамика
Молекулярно-кинетическая теория
3.2. Основное уравнение МКТ газов. Температура
Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).
В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной (рис. 3.2.1).
| Рисунок 3.2.1. Упругое столкновение молекулы со стенкой |
Поэтому изменение импульса молекулы будет равно 2m0υx, где m0 – масса молекулы.
Выделим на стенке некоторую площадку S (рис. 3.2.2). За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости υx, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υxΔt.
| Рисунок 3.2.2. Определение числа столкновений молекул с площадкой S |
Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nSυxΔt. Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку S за время Δt равно Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2m0υx, то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать:
Разделив обе части на SΔt, получим:
где p – давление газа на стенку сосуда.
При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так.
В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла. Дж. Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 3.2.3 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от υ до υ + Δυ. Это число равно площади выделенного на рис. 3.2.3 столбика.
| Рисунок 3.2.3. Распределение молекул по скоростям. T2 > T1 |
Характерными параметрами распределения Максвелла являются наиболее вероятная скорость υв, соответствующая максимуму кривой распределения, и среднеквадратичная скорость где – среднее значение квадрата скорости.
С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υв и υкв увеличиваются.
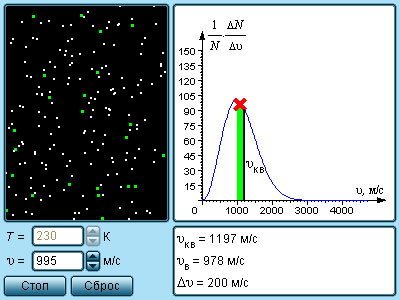 |
Модель. Распределение Максвелла |
Чтобы уточнить формулу для давления газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице объема, разбиты на группы, содержащие n1, n2, n3 и т. д. молекул с проекциями скоростей υx1, υx2, υx3 и т. д. соответственно. При этом Каждая группа молекул вносит свой вклад в давление газа. В результате соударений со стенкой молекул с различными значениями проекций υxi скоростей возникает суммарное давление
Входящая в это выражение сумма – это сумма квадратов проекций υx всех n молекул в единичном объеме газа. Если эту сумму разделить на n, то мы получим среднее значение квадрата проекции скорости молекул:
Теперь формулу для давления газа можно записать в виде
Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:
Последнее равенство вытекает из формулы:
Формула для среднего давления газа на стенку сосуда запишется в виде
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул n на среднюю кинетическую энергию поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то (N – число молекул в сосуде). В этом случае изменение давления Δp пропорционально изменению средней кинетической энергии.
Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде неизменного объема? Какую физическую величину нужно изменить, чтобы изменилась средняя кинетическая энергия Опыт показывает, что такой величиной является температура.
Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.
Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.
Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).
Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (TF), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,
Особое место в физике занимают газовые термометры (рис. 3.2.4), в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.
| Рисунок 3.2.4. Газовый термометр с постоянным объемом |
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки p0 и p100 на график, а затем провести между ними прямую линию (рис. 3.2.5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна -273,15 °С и не зависит от свойств газа. На опыте получить путем охлаждения газ в состоянии с нулевым давлением невозможно, так как при очень низких температурах все газы переходят в жидкое или твердое состояние.
| Рисунок 3.2.5. Зависимость давления газа от температуры при V = const |
Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой K. Например, комнатная температура TС = 20 °С по шкале Кельвина равна TК = 293,15 К.
Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.
Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия.
Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0,01 °С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К.
Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров.
Таким образом, давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p ~ T. С другой стороны, опыт показывает, что при неизменных объеме V и температуре T давление газа изменяется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда
где N – число молекул в сосуде, NА – постоянная Авогадро, n = N / V – концентрация молекул (т. е. число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать:
где k – некоторая универсальная для всех газов постоянная величина. Ее называют постоянной Больцмана, в честь австрийского физика Л. Больцмана, одного из создателей молекулярно-кинетической теории. Постоянная Больцмана – одна из фундаментальных физических констант. Ее численное значение в СИ равно:
Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить:
Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.
Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул.
Следует обратить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не зависит от ее массы. Броуновская частица, взвешенная в жидкости или газе, обладает такой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частицы. Этот вывод распространяется и на случай, когда в сосуде находится смесь химически невзаимодействующих газов, молекулы которых имеют разные массы. В состоянии равновесия молекулы разных газов будут иметь одинаковые средние кинетические энергии теплового движения, определяемые только температурой смеси. Давление смеси газов на стенки сосуда будет складываться из парциальных давлений каждого газа:
p = p1 + p2 + p3 + … = (n1 + n2 + n3 + …)kT.
В этом соотношении n1, n2, n3, … – концентрации молекул различных газов в смеси. Это соотношение выражает на языке молекулярно-кинетической теории экспериментально установленный в начале XIX столетия закон Дальтона: давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений.
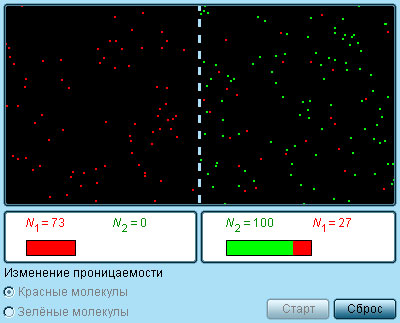 |
Модель. Полупроницаемая мембрана |
Источник
