Число столкновений о стенку сосуда
Рассмотрим находящийся в равновесии газ, заключенный в некотором сосуде. Возьмем элемент поверхности сосуда и подсчитаем число ударов молекул об этот элемент за время
Выделим из N молекул, заключенных в сосуде, те молекул, величина скорости которых заключена в пределах от v до
Из числа этих молекул направления движения, заключенные внутри телесного угла будет иметь количество молекул, равное
(см. ). Из выделенных таким образом молекул долетят за время до площадки и ударятся о нее J) молекулы, заключенные в косом цилиндре с основанием и высотой (рис. 95.1).
Рис. 95.1.
Количество этих молекул равно
(V — объем сосуда). Чтобы получить полное число ударов молекул о площадку , нужно просуммировать выражение (95.2) по телесному углу (отвечающему изменениям от 0 до и изменениям от 0 до ) и по скоростям в пределах от 0 до , где — наибольшая скорость, которой могут обладать молекулы в данных условиях (см. предыдущий параграф).
Начнем с суммирования по направлениям. Для этого представим в виде (см. (94.4)) и произведем интегрирование выражения (95.2) по 0 в пределах от 0 до и по в пределах от 0 до
Интегрирование по дает интеграл по равен 1/2. Следовательно,
Это выражение дает число ударов о площадку AS за время молекул, летящих в направлениях, заключенных в пределах телесного угла и имеющих величину скорости от v до .
Суммирование по скоростям дает полное число ударов молекул о площадку за время
Выражение
представляет собой среднее значение величины скорости V. Заменив в (95.4) интеграл произведением получим, что
Здесь есть число молекул газа в единице объема.
Наконец, разделив выражение (95.5) на и найдем число ударов молекул газа об единицу поверхности стенки в единицу времени:
Полученный результат означает, что число ударов пропорционально количеству молекул в единице объема («концентрации» молекул) и среднему значению величины Заметим, что величина (95.6) представляет собой плотность потока молекул, падающего на стенку.
Представим себе в газе воображаемую единичную площадку. Если газ находится в равновесии, через эту площадку будет пролетать в обоих направлениях в среднем одинаковое количество молекул, причем количество молекул, пролетающих в единицу времени в каждом из направлений, также определяется формулой (95.6).
С точностью до числового коэффициента выражение (95.6) может быть получено с помощью следующих упрощенных рассуждений. Допустим, что молекулы газа движутся только вдоль трех взаимно перпендикулярных направлений. Если в сосуде содержится N молекул, то в любой момент времени вдоль каждого из направлений будет двигаться молекул, причем половина из них (т. е. молекул) движется вдоль данного направления в одну сторону, половина в другую. Следовательно, в интересующем нас направлении (например, по нормали к данному элементу стенки сосуда) движется 1/6 часть молекул.
Предположим, кроме того, что все молекулы движутся с одинаковой скоростью, равной Тогда за время до элемента стенки долетят все движущиеся по направлению к нему молекулы, заключенные в объеме цилиндра с основанием и высотой (рис. 95.2). Число этих молекул равно Соответственно число ударов об единичную площадку в единицу времени оказывается равным
Полученное выражение отличается от (95.6) лишь значением числового множителя (1/6 вместо 1/4).
Сохранив предположение о движении молекул в трех взаимно перпендикулярных направлениях, но отказавшись от допущения об одинаковости скоростей молекул, следует выделить из числа молекул в единице объема те молекул, скорости которых лежат в интервале от v до
Рис. 95.2.
Количество молекул, имеющих такие скорости и долетающих до площадки за время равно
Полное число ударов получим, проинтегрировав выражение (95.8) по скоростям:
Наконец, разделив на и , получим формулу (95.7). Таким образом, предположение об одинаковости скоростей молекул не влияет на результат, получаемый для числа ударов молекул о стенку. Однако, как мы увидим в следующем параграфе, это предположение изменяет результат вычислений давления.
Источник
Получим формулу для вычисления числа ударов молекул в единицу времени о единичную площадь стенки сосуда, в котором находится газ.
Возьмем на стенке сосуда, бесконечно малую площадку dS, перпендикулярную оси Z системы координат XYZ ( рис. 8).
На этой площадке , как на основании, построим бесконечно узкий цилиндр с осью, имеющей направление, определяемое сферическими углами j и J,идлина которой равна vdt, где v – скорость молекулы, dt – промежуток времени. Объем этого цилиндра
, (1.4.1)
а число молекул в нем dn=ndV, где n – концентрация молекул в сосуде. Из-за хаотичности движения не все dn молекул достигнут площадки dS за время dt. Ее достигнут только те из молекул, которые, во-первых, движутся в направлении к площадке dS и, во-вторых, имеют скорости, близкие к u, при этом за время dt они проходят расстояние udt, равное длине образующей цилиндра, и достигают площадки dS. Найдем число таких молекул в объеме dV цилиндра.
И если к моменту времени t эти молекулы находились в объеме dV цилиндра, тогда время от t до t+dt все они достигнут площадки dS.
Р и с. 8
Обозначим через dnu число молекул в единице объема газа, которые имеют скорости, заключенные в интервале (u, u+du). Пусть среди этих молекул молекул в единице объема имеют направления движения, определяемые сферическими углами, взятыми из интервалов (j,j+dj) и (J,J+dJ). Согласно формуле (1.3.5), количество таких молекул в единице объема газа равно
(1.4.2)
Число же указанных молекул в объеме dV рассматриваемого цилиндра
dnu,J,j=dnu,J,j × dV (1.4.3)
С учетом формул (1.4.1) и (1.4.2) выражение (1.4.3) примет вид
(1.4.4) Таким образом, среди всех молекул, находящихся в объеме dV цилиндра, dnu,J,j молекул имеют близкие к u скорости, и их направления движения определяются углами, близкими к углам J и j. Однако из объема V, занимаемого газом, к площадке dS подлетают молекулы с других направлений и с иными скоростями. Чтобы учесть эти молекулы, необходимо проинтегрировать выражение (1.4.4) по всем возможным углам j и J и скоростям u:
(1.4.5)
Сферический угол J в общем случае изменяется от до p. В выражении (1.4.5) интегрирование по J произведено от до p/2, так как при интегрировании по J в пределах от p/2 до p рассматриваемые молекулы, как легко видеть из рис.8, будут иметь направление движения, соответствующее их удалению от площадки.
Разделив обе части соотношения (1.4.5) на dtdS, получим
(1.4.6)
Таким образом, выражение (1.4.6) определяет число ударов молекул газа в единицу времени о единичную площадку стенки сосуда.
Для выяснения смысла величины интеграла в выражении (1.4.6) умножим и разделим его на концентрацию молекул n=N/V.
(1.4.7)
Если обозначить через dNu число молекул в объеме V, которые имеют скорость от u до u + du, то dnu=dNu /V будет определять число таких молекул в единице объема газа. Величина же
(1.4.8)
при больших N представляет собой вероятность того, что случайно “взятая” в газе молекула будет иметь скорость, заключенную в интервале (u,u+du). Эта вероятность связана с функцией распределения (плотностью вероятности) следующим соотношением (см. А.23):
(1.4.9)
Функция распределения молекул по скоростям F(u) является важнейшей характеристикой равновесного состояния газа. Ее явный вид будет получен в последующих параграфах из весьма общих предпосылок.
С учетом формул (1.4.8) и (1.4.9), выражение (1.4.7) примет вид
(1.4.10)
Интеграл, стоящий в соотношении (1.4.10), представляет среднее значение скорости (см. формулу (А.25) Приложения А):
(1.4.11)
Поэтому
(1.4.12)
Как видно из выражения (1.4.12), число ударов молекул газа в единицу времени о единичную площадку пропорционально концентрации и средней скорости их движения, что находится в полном согласии с нашей интуицией.
Пример
1. В космическом корабле находится воздух объема V с концентрацией n0, поддерживаемый при постоянной температуре. За бортом корабля вакуум. Найти зависимость концентрации молекул воздуха в корабле от времени, если в тонкой части его стенки образовалось малое отверстие площади S?
Решение. Пусть через время t после образования отверстия концентрация воздуха в корабле стала равной n(t). Тогда число молекул воздуха, влетающих в отверстие площади S за время dt (от момента t до t+dt), согласно формуле (1.4.5)
dn= n(t)<u>Sdt (1.4.13)
Эти молекулы покидают кабину корабля. С другой стороны, это число молекул можно выразить иначе.
Изменение концентрации воздуха в корабле за время dt (от t до t+dt)
Откуда находим
dn = –Vdn (1.4.14)
Сравнивая выражения (1.36) и (1.37), получаем
(1.4.15)
Проинтегрируем равенство (1.4.15).
Откуда находим искомую зависимость концентрации от времени
(1.4.16)
Источник
§9. Молекулярно-кинетическая теория идеального газа
9.1. Модель идеального газа в молекулярно-кинетической теории
Законы идеальных газов, найденные опытным путём, находят довольно простое объяснение в молекулярно-кинетической теории (МКТ). Она исходит при этом из упрощённых представлений о строении газа. Это обусловлено рядом причин, в частности, неточным знанием сил взаимодействия между молекулами. Однако, как оказывается, даже такая упрощённая модель газа позволяет найти уравнение состояния, правильно описывающее его поведение.
В молекулярно-кинетической теории принимается следующая идеализированная модель газа – идеальный газ. Молекулы газа считаются твёрдыми, абсолютно упругими шариками, причём размеры молекул малы по сравнению со средним расстоянием между ними. Это означает, что собственный суммарный объём молекул значительно меньше объёма сосуда, в котором находится газ. Взаимодействие между молекулами проявляется только при непосредственном столкновении их друг с другом. Между столкновениями молекулы движутся по инерции. Движение молекул подчиняется законам механики Ньютона.
Для нахождения уравнения состояния газа необходимо сделать ещё важное упрощающее предположение, а именно, считать движение любой молекулы газа беспорядочным, хаотичным.
Аккуратный вывод основного уравнения молекулярно-кинетической теории идеального газа требует принимать во внимание ряд моментов, например, наличие в газе молекул, движущихся с разными по величине скоростями, столкновения молекул между собой, характер столкновения отдельной молекулы со стенкой сосуда (упругий или неупругий). В разделе 7.3 будет рассмотрен упрощённый вариант вывода основного уравнения молекулярно-кинетической теории.
9.2. Давление идеального газа
Давление, которое оказывает газ на стенку сосуда, есть результат ударов молекул газа о стенку. Если бы в сосуде содержалось всего несколько молекул, то их удары следовали бы друг за другом редко и беспорядочно. Поэтому нельзя было бы говорить ни о какой регулярной силе давления, действующей на стенку. Стенка подвергалась бы отдельным практически мгновенным бесконечно малым толчкам. Если же число молекул в сосуде очень велико, то велико и число ударов их о стенку сосуда. Одновременно о стенку сосуда ударяется громадное количество молекул. Очень слабые силы отдельных ударов складываются при этом в значительную по величине и почти постоянную силу, действующую на стенку. Среднее по времени значение этой силы, отнесённое к единичной площадке, и есть давление газа, с которым имеет дело термодинамика.
Пусть в сосуде объёма $$ V$$ находятся $$ N$$ одинаковых молекул идеального газа, а $$ {m}_{0}$$ – масса одной молекулы. В рамках молекулярно-кинетической теории показывается, что давление $$ p$$ газа определяется выражением:
p=m0nv2¯/3p = m_0nbar{v^2}/3, (11)
где $$ n=N/V$$ – концентрация молекул газа, v2¯bar{v^2} – среднее значение квадрата скорости молекулы. Выражение (11) называют основным уравнением молекулярно-кинетической теории идеального газа.
Заметим, что величина m0v2¯/2m_0bar{v^2}/2 есть средняя кинетическая энергия E¯bar{E} поступательного движения молекулы. Поэтому полученную формулу можно представить в другом виде:
p=2nE¯/3p = 2nbar E / 3. (12)
Ниже приводится один из способов вывода уравнения (11). Данный раздел при первом прочтении можно пропустить.
9.3* Вывод основного уравнения МКТ идеального газа
Вычислим среднее давление газа на стенку сосуда.
Для простоты будем считать, что удар молекулы о стенку происходит абсолютно упруго, а сама стенка идеально гладкая и молекула после удара отражается от неё под тем же углом, под каким она падала на стенку (см. рис. 11), или, как говорят, зеркально (однако ясно, что никаких гладких стенок не существует: ведь сама стенка состоит из молекул).
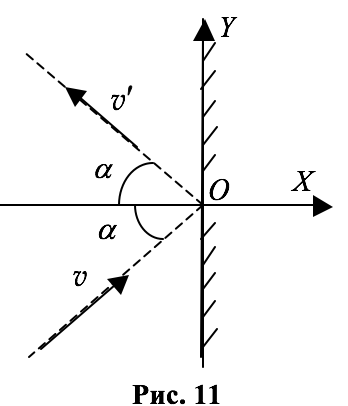
Введём систему координат, направив ось $$ OX$$ перпендикулярно стенке, а ось $$ OY$$ – вдоль стенки (см. рис. 11).
Пронумеруем все молекулы от $$ i=1$$ до $$ i=N$$. Пусть $$ {v}_{i,x},({v}_{i,x}>0) -$$ проекция скорости $$ i$$-ой молекулы на ось $$ OX$$ до удара. При абсолютно упругом ударе о стенку проекция скорости на ось $$ OX$$ изменяет знак: $$ {v}_{i,x}^{text{‘}}=-{v}_{i,x}$$. Изменение проекции импульса молекулы на ось $$ OX$$ при столкновении молекулы со стенкой равно:
$$ mathrm{Delta }{p}_{i,x}={m}_{0}{v}_{i,x}^{text{‘}}-{m}_{0}{v}_{i,x}=-2{m}_{0}{v}_{i,x}$$,
а передаваемый стенке импульс равен:
$$ mathrm{Delta }{p}_{i,x,mathrm{стен}}=-mathrm{Delta }{p}_{i,x}=2{m}_{0}{v}_{i,x}$$.
Так как давление газа не зависит от формы сосуда, возьмём для простоты сосуд в форме куба с ребром $$ l$$. Тогда промежуток времени между двумя последовательными столкновениями молекулы с одной и той же стенкой составит $$ {tau }_{i}=2l/{v}_{i,x}$$, а за большой интервал времени $$ t$$ она столкнётся со стенкой $$ {N}_{mathrm{столк},i}=t/{tau }_{i}$$ раз. Переданный стенке одной молекулой за это время импульс равен:
`2m_0v_(i,x)*N_(“столк”,i)=2m_0v_(i,x)*(v_(i,x)t)/(2l)=m_0v_(i,x)^2*t/l`.
Так как в сосуде находятся $$ N$$ молекул, то полный переданный стенке импульс всех молекул равен:
$$ mathrm{Delta }{p}_{x,sum }=sum _{i=1}^{i=N}Delta {p}_{i,x,mathrm{стен}}={displaystyle frac{{m}_{0}t}{l}}sum _{i=1}^{i=N}{v}_{i,x}^{2}$$.
Среднюю силу давления на стенку можно получить, разделив полный передаваемый стенке импульс на время $$ t$$:
`F_(x,”ср”)=(Deltap_(x,sum))/t=m_0/l sum_(i=1)^(i=N) v_(i,x)^2`,
а давление $$ p -$$ разделив эту силу на площадь стенки $$ S={l}^{2}$$:
`p=(F_(x,”ср”))/S=m_0/l^3 sum_(i=1)^(i=N) v_(i,x)^2=m_0/V sum_(i=1)^(i=N) v_(i,x)^2`.
Здесь учтено, что объём сосуда $$ V={l}^{3}$$. Если ввести среднее значение квадрата проекции скорости одной молекулы:
`bar(v_x^2)=1/N sum_(i=1)^(i=N) v_(i,x)^2`,
то для давления $$ p$$ получаем:
$$ p={displaystyle frac{{m}_{0}N}{V}}overline{{v}_{x}^{2}}$$.
Входящую в это выражение величину $$ overline{{v}_{x}^{2}}$$ можно выразить через среднее значение квадрата скорости молекулы. Из соотношения $$ {v}^{2}={v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}$$ для средних значений имеем: $$ overline{{v}^{2}}=overline{{v}_{x}^{2}}+overline{{v}_{y}^{2}}+overline{{v}_{z}^{2}}$$. Так как движение молекул беспорядочное, то все направления движения равновероятны и средние значения квадратов проекций на любое направление должны быть равны $$ overline{{v}_{x}^{2}}=overline{{v}_{y}^{2}}=overline{{v}_{z}^{2}}$$. Отсюда получаем: $$ overline{{v}^{2}}=3overline{{v}_{x}^{2}}$$, что позволяет записать выражение для давления в виде:
$$ p={displaystyle frac{1}{3}}{displaystyle frac{{m}_{0}N}{V}}overline{{v}^{2}}, mathrm{или} p={displaystyle frac{1}{3}}{m}_{0}noverline{{v}^{2}}$$,
где $$ n=N/V$$ концентрация молекул газа.
Источник
Рассмотрим
находящийся в равновесии газ, заключенный
в некотором сосуде. Допустим, что молекулы
газа движутся только вдоль трех взаимно
┴ направлений. Это можно допустить
из-за хаотичности движения молекул.
Если в сосуде находится N
молекул, то в любой момент времени вдоль
каждого из направлений будет двигаться
N/3
молекул и половина из них – N/6
вдоль данного направления в одну сторону,
а вторая половина – в другую. Следовательно,
в интересующем нас направлении по
нормали к данному элементу ΔS
стенки сосуда движется N/6
молекул, а для единицы объема –
![]() ,n
,n
– концентрация молекул.
Пусть
все молекулы движутся с одинаковой
средней скоростью <v>.
За время Δt
элемента стенки ΔS
достигают все молекулы, находящиеся в
параллелипипеде с площадью основания
ΔS
и длиной
![]() <v>Δt.
<v>Δt.
Их число Δν = (n/6)ΔS<v>Δt,
следовательно, число ударов о единичную
площадку в единицу времени
Δν/ΔSΔt
= (n/6)<v>.
Если
отказаться от допущения, что все молекулы
движутся с одинаковой скоростью v
= <v>,
то необходимо выделить в единице объема
молекулы, скорости которых лежат в
интервале от v
до v+dv.
Их число –![]() .
.
Количество ударов таких молекул,
долетающих до площадки ΔS
за время Δt
равно dνv
= (1/6)(dnvΔS
vmax
vΔt).
vmax
Полное число ударов:
Δν
=
![]() dνv
dνv
= 1/6ΔSΔt
![]() vdnv
vdnv
= Выражение
![]()
![]() vdnv
vdnv
по
определению является средней скоростью
молекулы, тогда Δν
= 1/6ΔSΔtn<v>
, т.е., получили то же самое значение
числа ударов.
3.4 Давление газа на стенку сосуда
Давление
по определению можно записать:
![]() ,
,
а поскольку, из второго закона Ньютона:![]() ,
,
то![]() .
.
Значит, необходимо вычислить импульс![]() ,
,
передаваемый всеми молекулами со всеми
скоростями единице площади за единицу
времени.
Число
молекул со скоростью v
из общего количества n,
долетающих до площадки ΔS
за время Δt
равно:
dνv
= (1/6)(dnvΔSvΔt)
Далее,
умножив это число на импульс, сообщаемый
каждой молекулой при ударе равный –
2mv,
получим импульс, сообщаемый площадке
ΔS
за время Δt
этими молекулами. Изменение импульса
одной молекулы равно K2-K1=
-2mv,
значит, импульс передаваемый молекулой
сте
vmax
нке равен +2mv.
vmax
Импульс, передаваемый
молекулами со скоростями, лежащими в
интервале от v
до v +dv
равен
![]() v.
v.
Импульс,
передаваемый всеми молекулами со всеми
скоростями:
![]() K
K
=
![]() (1/6)(dnvΔSvΔt)2mv
(1/6)(dnvΔSvΔt)2mv
= 1/3 m
ΔSΔt
![]() v2dnv
v2dnv
(*)
Выражение
![]()
![]() v2dnv
v2dnv
представляет собой среднее значение
квадрата скорости молекул, тогда,
заменив в (*) интеграл и, разделив это
выражение на ΔS
и Δt,
получим давление газа на стенку сосуда:
р
= 1/3mn<v2>
т.к.
m<v2>/2
= <εпост>
по определению, получим:
р
=2/3n<εпост>
–
основное
уравнение молекулярно- кинетической
теории. Это
уравнение раскрывает физический смысл
макропараметра р: давление определяется
средним значением кинетической энергии
поступательного
движения молекул.
3.5 Средняя энергия молекул
Из
уравнения состояния идеального газа
p=nkT
и выражения для давления газа на стенку
сосуда р =2/3n<εпост>
следует, что
<εпост>
= 3/2kT
(1), откуда можно заключить, что температура
есть величина, прямо пропорциональная
средней энергии поступательного движения
молекул.
Поступательно
движутся молекулы газа. Молекулы твердых
и жидких тел совершают колебания вблизи
положений равновесия.
Из
выражения (1) видно, что <εпост>
зависит только от Т и не зависит от массы
молекулы.
Т.к.,
<εпост>
= <mv2/2>
= m<v2>/2,
то из сравнения с выражением (1), получим:
<v2>
= 3kT/m
а средняя
квадратичная скорость:
vср.кв.
= √<v2>
= √3kT/m
.
Можно
представить <v2>
= <v2x>+<v2y>+<v2z>
= 3<v2x>,
поскольку, все направления движения
молекул равноправны, т.е., <v2x>
= <v2y>
= <v2z>,
тогда:
<v2x>
= 1/3<v2>
= kT/m
Формула (1) определяет
энергию поступательного движения
молекул. Наряду с этим движением возможны
также вращение молекул и колебания
атомов, входящих в состав молекул.
Например, для двухатомной жесткой
молекулы это вращение вокруг двух
взаимно перпендикулярных осей, проходящих
через центр масс молекулы. Эти виды
движения также связаны с запасом энергии
молекулы. Ее полную энергию позволяет
определить, устанавливаемое статистической
физикой, положение о равнораспределении
энергии по степеням свободы молекулы.
Такую гипотезу впервые высказал Больцман.
Числом степеней свободы механической
системы называется количество независимых
величин, с помощью которых может быть
задано ее положение. Положение материальной
точки определяется в пространстве
значением трех координат, она имеет три
степени свободы. Одноатомной молекуле
следует приписывать три степени свободы,
двухатомной: в зависимости от характера
связи между атомами – либо три
поступательных и две вращательных
(жесткая связь), т.е. всего пять степеней;
либо n
= 3+2+1=6 с
учетом колебательной степени свободы
для нежесткой молекулы.
Поскольку
ни одна из поступательных степеней
свободы не имеет преимущества перед
остальными, на каждую из них приходится
в среднем одинаковая энергия 1/2kT.
Согласно закону равнораспределения на
каждую степень свободы молекулы
приходится в среднем одинаковая энергия,
равная 1/2kT.
Согласно закону среднее значение энергии
одной молекулы <ε>
будет тем больше, (при одинаковой Т), чем
сложнее молекула и чем больше у нее
степеней свободы. При
определении <ε>
необходимо учесть, что колебательная
степень свободы обладает вдвое большей
«энергетической емкостью» по сравнению
с поступательной или вращательной. Это
объясняется тем, что колебательное
движение связано с наличием кинетической
и потенциальной энергии, поэтому на
колебательную степень приходится
(1/2kT+1/2kT)
= kT,
т.е., одна
половинка в виде εкин
, а вторая – εпост.
Т.о.
средняя энергия молекулы: <ε>
= (i/2)(kT),
Где
i- сумма
поступательных, вращательных и удвоенного
числа колебательных степеней свободы
молекул.
i
= nпост+nвращ+2nкол
, здесь n
– число степеней свободы.
Для
молекул с жесткой связью i
совпадает с числом степеней свободы.
Внутренняя
энергия и теплоемкость идеальных газов
В идеальном газе
молекулы не взаимодействуют между
собой, внутренняя энергия одного моля
газа:
Uм
= NA<ε>
= i/2 NAkT
= i/2 RT . Uм
= i/2RT.
Если
вспомнить, что по определению: Cv
= δQ/dT
= dU/dT,
поскольку, δQ
= dU+pdV,
а для изохорного процесса
dV
= 0.
Тогда
Cv
= (i/2)
R
, а, учитывая, что Cр
= Cv+R,
получим:
Cр
= (i+2)/2
R
Следовательно,
коэффициент
Пуассона
γ
= Cp/Cv
= (i+2)/i
, таким
образом, γ определяется числом и
характером степеней свободы молекулы.
Согласно
этой ф-лы для одноатомной молекулы i
= 3 и γ =
1,67; жесткой двухатомной
i =5 и γ =
1,4; упругой двухатомной i
= 7, а γ = 1,29. В области температур, близких
к комнатной, это хорошо согласуется с
опытом. Однако, в широком температурном
интервале это не так. Оказывается, что
вращательная и колебательная энергии
молекулы квантованы. При низких Т
вращательные и колебательные степени
свободы не возбуждены. Молекула Н2
, например,ведет себя
как одноатомная в этой области температур,
i
= 3. В области Т ≈ 500К вращательные степени
«разморожены» <ε>
> εвращ
и молекула Н2
ведет себя
как жесткая двухатомная с = 3+2 = 5. При
Т>1000К энергии <ε>
достаточно для возбуждения колебательной
степени свободы, «включены» все степени
свободы, i
= 7.
Источник
