Что такое давление жидкости на дно и стенки сосуда

Поскольку на жидкость действует сила тяжести, жидкое вещество обладает весом. Вес — это сила, с которой оно давит на опору, т. е. на дно сосуда, в который налито. Закон Паскаля говорит: давление на жидкость передается в любую ее точку, не меняя своей силы. Как же рассчитать давление жидкости на дно и стенки сосуда? Будем разбираться в статье, используя наглядные примеры.
Опыт
Представим, что у нас есть цилиндрический сосуд, в который налита жидкость. Обозначим высоту слоя жидкости h, площадь дна сосуда — S, а плотность жидкости — ρ. Искомое давление — это P. Его вычисляют путем деления силы, действующей под углом 90° к поверхности, на площадь этой поверхности. В нашем случае поверхность — это дно емкости. P = F/S.
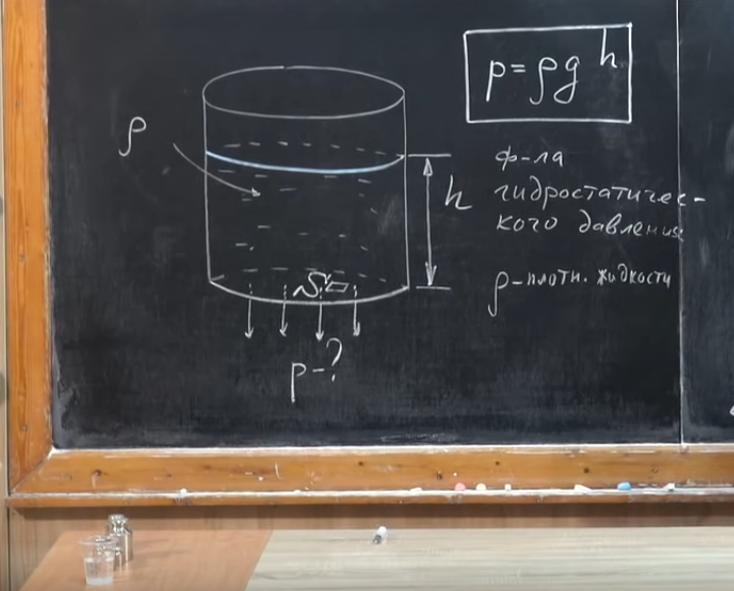
Сила давления жидкости на дно сосуда — это вес. Он равен силе давления. Наша жидкость неподвижна, поэтому вес равен силе тяжести (Fтяж ), действующей на жидкость, а значит, и силе давления (F=Fтяж). Fтяж находят так: умножают массу жидкости (m) на ускорение свободного падения (g). Масса может быть найдена, если известно, какова плотность жидкости и каков ее объем в сосуде. m = ρ×V. Сосуд имеет цилиндрическую форму, поэтому его объем мы будем находить, умножив площадь основания цилиндра на высоту слоя жидкости (V = S×h).
Расчет давления жидкости на дно сосуда
Вот величины, которые мы можем вычислить: V = S×h; m = ρ×V; F = m×g. Подставим их в первую формулу и получим такое выражение: P = ρ×S×h×g/S. Сократим площадь S, стоящую в числителе и знаменателе. Она исчезнет из формулы, а это значит, что давление на дно не зависит от площади сосуда. Кроме того, оно не зависит и от формы емкости.
Давление, которое жидкость создает на дно сосуда, называется гидростатическим. “Гидро” — это “вода”, а статическое — это потому, что жидкость неподвижна. По формуле, полученной после всех преобразований (P = ρ×h×g), определите давление жидкости на дно сосуда. Из выражения видно, что чем более плотная жидкость, тем больше ее давление на дно сосуда. Разберем подробнее, что собой представляет величина h.
Давление в толще жидкости
Допустим, мы нарастили сосуд снизу еще на некоторую величину, добавили дополнительное пространство для жидкости. Если мы поместим в емкость рыбку, давление на нее будет одинаковым в сосуде из предыдущего опыта и во втором, увеличенном? Изменится ли давление от того, что под рыбкой еще есть вода? Нет, потому что сверху находится определенный слой жидкости, на нее действует сила тяжести, значит, вода обладает весом. А то, что снизу, не имеет никакого значения. Следовательно, мы можем найти давление в самой толще жидкости, и h — это будет глубина. Она необязательно является расстоянием до дна, дно может быть и ниже.

Представим, что мы развернули рыбку на 90°, оставив ее на той же глубине. Изменится ли от этого давление на нее? Нет, потому что на глубине оно одинаково во всех направлениях. Если мы приблизим рыбку прямо к стенке сосуда, изменится ли давление на нее, если она будет оставаться на той же глубине? Нет. Во всех случаях давление на глубине h будет вычисляться по той же формуле. Значит, эта формула позволяет найти давление жидкости на дно и стенки сосуда на глубине h, т. е. в толще жидкости. Чем глубже, тем оно больше.
Давление в наклонном сосуде
Представим, что у нас есть трубка длиной около 1 м. Мы налили в нее жидкость так, что она заполнена целиком. Возьмем точно такую же трубку, наполненную до краев, и разместим ее под наклоном. Сосуды одинаковы и заполнены одной и той же жидкостью. Следовательно, масса и вес жидкости и в первой, и во второй трубке равны. Будет ли одинаковым давление в точках, расположенных на дне этих емкостей? На первый взгляд кажется, что давление P1 равно P2, поскольку масса жидкостей одинакова. Предположим, что это так, и проведем эксперимент, чтобы проверить.
Соединим нижние части этих трубок маленькой трубочкой. Если наше предположение о том, что P1 = P2, верное, то перетечет ли куда-то жидкость? Нет, потому что на ее частицы будут действовать силы противоположного направления, которые будут компенсировать друг друга.
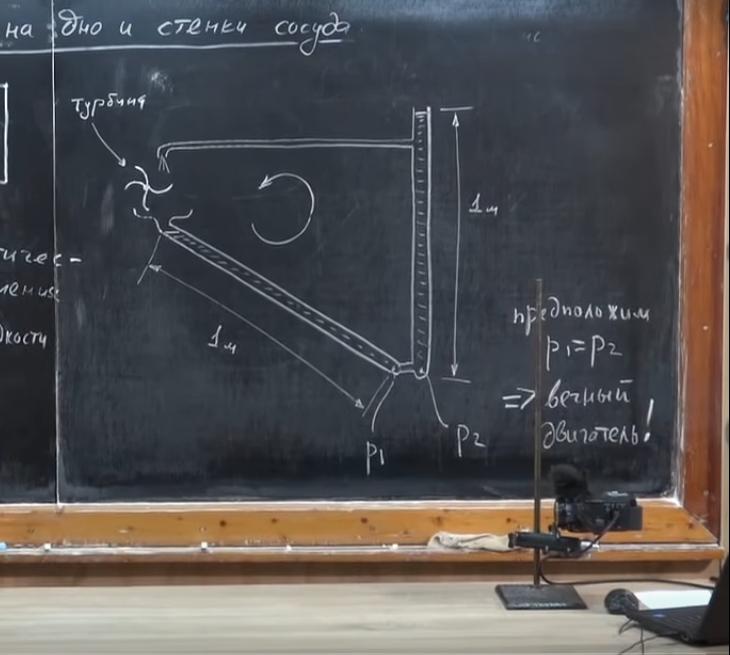
Давайте приделаем к наклонный трубке сверху воронку. А на вертикальной трубке проделаем отверстие, в него вставим трубочку, которая загибается вниз. Давление на уровне отверстия больше, чем на самом верху. Значит, жидкость будет перетекать по тоненькой трубочке и наполнять воронку. Масса жидкости в наклонной трубке будет увеличиваться, жидкость потечет из левой трубки в правую, затем будет подниматься и циркулировать по кругу.
А теперь установим над воронкой турбину, которую соединим с электрическим генератором. Тогда эта система самостоятельно, без какого-либо вмешательства будет вырабатывать электроэнергию. Она будет работать без остановки. Казалось бы, это и есть «вечный двигатель». Однако еще в XIX веке Французская академия наук отказалась принимать любые подобные проекты. Закон сохранения энергии говорит о том, что создать «вечный двигатель» невозможно. Значит, наше предположение о том, что P1 = P2, неверное. На самом деле P1< P2. Как же тогда рассчитать давление жидкости на дно и стенки сосуда в трубке, которая расположена под наклоном?
Высота столба жидкости и давление
Чтобы это выяснить, проведем следующий мысленный эксперимент. Возьмем сосуд, наполненный жидкостью. Поместим в него две трубки из металлической сетки. Одну расположим вертикально, а другую – наклонно, таким образом, что ее нижний конец будет находиться на той же глубине, что и дно первой трубки. Поскольку емкости находятся на одинаковой глубине h, то давление жидкости на дно и стенки сосуда будет тоже одинаковым.

Теперь заделаем все отверстия в трубках. Из-за того, что они стали сплошными, давление в их нижних частях изменится? Нет. Хотя давление и одинаково, а сосуды равны по размеру, масса жидкости в вертикальной трубке меньше. Глубина, на которой находится нижняя часть трубки, называется высотой столба жидкости. Дадим определение данному понятию: это отсчитываемое по вертикали расстояние от свободной поверхности до данной точки жидкости. В нашем примере высота столба жидкости одинакова, поэтому и давление одинаково. В предыдущем опыте высота столба жидкости в правой трубке больше, чем в левой. Поэтому давление P1 меньше, чем P2.
Источник
Что такое давление жидкости
Наука гидростатика исследует ситуации, когда движение в жидкости отсутствует или скорость пренебрежимо мала, и позволяет понять некоторые свойства такой важной гидродинамической величины, как давление.
Теорема
Давление — физическая величина, описывающая силу, которая действует перпендикулярно поверхности на единицу ее площади. Для ее обозначения используется символ р или Р.
На опору под действием силы тяжести давят и твердые, и сыпучие вещества, но их воздействие отличается от гидростатического давления. Воздействие твердого тела определяется его весом, жидкости — ее глубиной. В газе и жидкости давящее воздействие на поверхности создается за счет хаотических столкновений молекул и связано с другими параметрами состояния вещества — например, температурой Т и плотностью (rho.)
Для жидкости, учитывая ее малую сжимаемость, вместо уравнения Клапейрона, учитывающего температуру и молярную массу газа, обычно используют условие несжимаемости, которое существенно упрощает уравнения гидроаэромеханики:
(rho = const.)
Сила гидростатического давления р на дно сосуда не зависит от его формы и изменяется пропорционально уровню налитой в сосуд жидкости и ее плотности в соответствии с основной гидростатической формулой:
(р = р_{0} + rhotimes gtimes h.)
(rho) здесь — плотность вещества, (р_{0}) — атмосферное давление, g — ускорение свободного падения, h — глубина погружения.
История открытия
Гидростатика как наука была достаточно хорошо известна еще в античные времена, поскольку она тесно связана с практической деятельностью людей. Для строительства лодок и кораблей, колодцев и различных гидравлических аппаратов, например, поршневых насосов, необходимо было понимать, как вода взаимодействует с твердыми материальными предметами.
Различие между давлением твердого тела и воды очень эффектно пояснил на опыте Блез Паскаль: всего лишь стакан воды, вылитый в высокую тонкую трубку, соединенную с наполненной водой закрытой бочкой, создал такое избыточное давление, что вода через щели брызнула наружу.
Определение
В 1653 году Паскаль сформулировал свой закон: давление, производимое на жидкость или газ, передается в любую точку одинаково.
Позже был сконструирован прибор, демонстрирующий действие закона Паскаля. Он называется шар Паскаля и представляет собой заполняемый водой шар с маленькими отверстиями, соединенный с цилиндрической рукояткой, внутри которой движется поршень. Внешнее давление, производимое поршнем, передается во все точки воды одинаково, и она выплескивается в виде одинаковых струек. Поэтому струйки, вытекающие из отверстий, расположенных в горизонтальной плоскости, оставляют на полу следы равной длины.
Факторы, влияющие на показатель
На давление жидкости могут влиять:
- ее плотность;
- атмосферное давление;
- температура;
- глубина сосуда;
- площадь дна сосуда.
Давление на дно и стенку сосуда
Закон Паскаля утверждает, что давление в любом месте покоящейся жидкости или газа по всем направлениям одинаково, причем оно одинаково передается по всему объему вещества. Таким образом, разницы между давлением на дно и на стенку нет.
Расчет давления жидкости на дно и стенки сосуда
Чтобы найти давление на дно сосуда, нужно взять приведенное выше основное уравнение гидростатики и подставить туда глубину, плотность и атмосферное давление.
В случае стенок непосредственно прилагать эту формулу можно только к бесконечно малым горизонтальным полоскам на боковых стенках сосуда. Чтобы рассчитать давление на стенки, нужно суммировать давление на все горизонтальные элементы их поверхности, используя правила интегрального исчисления. Паскаль, проведя эти расчеты, доказал, что от формы сосуда давление жидкости не зависит.
Единицы измерения
В международной системе единиц давление измеряется в Паскалях. Один Паскаль равен силе в один ньютон, производящей равномерное давление на единицу поверхности в один метр. Но на практике часто используют такую единицу измерения, как атмосфера, равную 76 см ртутного столба при нулевой температуре по Цельсию.
Определение
Атмосфера — внесистемная единица измерения, которая примерно означает давление атмосферы Земли на уровне Мирового океана.
Формулы расчета
Для описания процессов в гидравлических прессах или любых других системах, в которых давление собственно жидкостей ничтожно мало по сравнению с передаваемым им извне, используется формула закона Паскаля:
(р = frac{F}{S}.)
F — сила, с которой происходит воздействие на поверхности сосуда, S — площадь этой поверхности.
В учебных задачах обычно опускают такой параметр, как атмосферное давление, и используют для расчетов формулу:
(р = rhotimes gtimes h.)
Можно вывести эту формулу для сосудов, имеющих форму прямой призмы или цилиндра, из закона Паскаля.
(m = rhotimes V = rhotimes Stimes h)
Вес (Р = g times m = gtimes rhotimes Stimes h.)
Вес столба, давящего на дно сосуда, равен силе, и тогда:
(р = frac{Р}{S} = gtimes rhotimes Stimes frac{h}{S} = gtimes rhotimes h.)
Применение на практике
Для гидравлических механизмов, например, прессов, можно рассчитать пропорциональный изменению площади выигрыш в силе, зная, во сколько раз увеличивается площадь большего поршня по сравнению с меньшим.

Соотношение между полезной и затраченной работой описывается понятием КПД, коэффициент полезного действия, и рассчитывается по формуле:
(frac{F_{2}h_{2}}{F_{1}h_{1}})
Также закон Паскаля описывает работу жидкостных манометров, приборов для измерения давления, отличного от атмосферного. Давление в одном колене манометра вызывает повышение жидкости в другом колене — это явление называется избыточным столбом. По его высоте, соотнося ее с нанесенной шкалой, пользователь прибора узнает точную цифру в миллиметрах ртутного столба.
Гидростатический парадокс
Согласно гидростатическому парадоксу, давление жидкости на любую плоскую стенку равняется весу столба этой жидкости, давящему на основание, площадь которого равна площади этой стенки. Поэтому от формы емкости давление не зависит. Если емкость расширяется к горлышку, то вес содержимого распределяется по наклонным стенкам и передается вниз через стенки, не давя на дно, а если емкость к горлышку сужается, то содержимое давит на стенки снизу вверх, что уменьшает его воздействие на дно.
Источник
Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.
Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòàòè÷åñêèì.
Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:
1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:
2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
F=mg. (1.28)
Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:
m = pV, (1.29)
à îáúåì — ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:
V=Sh. (1.30)
Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:
F = pVg=pShg. (1.31)
Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:
pS = pSkg.
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:
p = phg.
Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.
Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàêæå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ — ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.
 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.
Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæàþùèõñÿ — áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñóäîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S — ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ — ñïîñîáíîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.
Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëåíèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâøèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëåíèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Источник
Что это такое?
В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.
Оно определяется отношением силы к площади, то есть его физический смысл – это сила, действующая на единицу площади (см2).
 Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.
Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.
Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.
Факторы, влияющие на показатель
При отсутствии внешнего воздействия, играют роль два фактора:
- высота столба;
- плотность.
Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.
Сверху на содержимое сосуда давит также атмосферный воздух. Поэтому в сообщающихся сосудах уровень одинаков, ведь в каждом из них над поверхностью атмосфера одна и та же.
Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:
- внешней силы;
- веса воды.
При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

На дно и стенку сосуда – в чем разница?
Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.
Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.
Наполнив сосуд, имеющий отверстия одного диаметра в стенках на разной высоте, можно наблюдать различный напор вытекающей струи. Чем выше отверстие – тем слабее струя. То есть, давление на стенки емкости тем больше, чем ближе ко дну.
Единицы измерения
 Давление воды измеряют в:
Давление воды измеряют в:
- паскалях – Па;
- метрах водяного столба – м. в. ст.
- атмосферах – атм.
Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).
Формулы расчета
Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).
Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.
Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.
Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.
Расчет давления воды на дно и стенки сосуда в видео:
Применение на практике
Примеры использования знаний свойств воды:
-
 Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм. - Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
- Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
- Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.
Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:
- выжимка масла из семян растений;
- спуск на воду со стапелей построенного судна;
- ковка и штамповка деталей;
- домкраты для подъема грузов.
Заключение
Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.
Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.
А какова Ваша оценка данной статье?
Источник
