Что такое разряжение в закрытых сосудах
ЛЕКЦИЯ 7 УРАВНЕНИЕ БЕРНУЛЛИ И ЕГО СЛЕДСТВИЯ
1. Линии тока и трубка тока. Условие неразрывности струи.
2. Уравнение Бернулли.
3. Следствия уравнения Бернулли.
4. Принцип работы инжектора, ингалятора.
5. Основные понятия и формулы.
6. Задачи.
7.1. Линии тока и трубка тока. Условие неразрывности струи
Течение жидкости изображается линиями тока –
линиями, касательные к которым в каждой точке совпадают с направлением
вектора скорости частиц. Течение жидкости называется установившимся, стационарным, если
скорости частиц в каждой точке потока со временем не изменяются (при
этом условии линии тока совпадают с траекториями частиц жидкости).
При стационарном течении линии тока остаются неизменными. Часть потока жидкости, ограниченная линиями тока, образует трубку тока. Частицы
жидкости не выходят за пределы трубки тока, поэтому через любое ее
сечение проходит одно и то же количество жидкости. Объем Q жидкости,
протекающей за единицу времени через любое сечение S, перпендикулярное
оси трубки тока, определяется формулой
где v – скорость движения частиц жидкости в данном сечении.
Для
идеальной жидкости, не подверженной действию сил трения, скорости
движения частиц во всех точках одного и того же поперечного сечения
трубы одинаковы. Эта общая скорость и входит в уравнение (7.1).
На частицы реальной жидкости действуют силы трения со стороны стенок трубы и со стороны соседних частиц. Поэтому скорость
частиц
жидкости в поперечном сечении трубы различна: она максимальна в центре
трубы и уменьшается до нуля у ее стенок. В этом случае в формуле (7.1) v – это средняя скорость течения жидкости в данном сечении.
Условие неразрывности струи: при
стационарном течении несжимаемой жидкости через любые сечения трубки
тока каждую секунду протекают одинаковые объемы жидкости, равные
произведению площади сечения на среднюю скорость движения ее частиц.
Уравнение (7.1) выражает условие неразрывности струи. Оно устанавливает соотношение между скоростями течения жидкости в различных сечениях трубки тока:
Если
жидкость движется по трубе переменного сечения, то скорость ее движения
обратно пропорциональна площади сечения трубок (рис. 7.1).
Рис. 7.1. Движение жидкости в трубе с разными сечениями. Длина стрелок изображает среднюю скорость течения жидкости
Площадь сечения пропорциональна квадрату диаметра трубки (S = πd2/4), поэтому если диаметр трубки в сечении С вдвое меньше,
чем в сечении А, то площадь поперечного сечения С в четыре раза меньше,
чем площадь сечения А. Следовательно, и скорость потока в сечении С
будет в четыре раза больше, чем в сечении А.
Уравнение неразрывности струи при протекании крови в сосудах
Кровеносная
система человека – это сложная замкнутая система эластичных трубок
разного диаметра. В нее входят: аорта, артерии, артериолы, капилляры,
венулы, вены. Из сердца кровь поступает в аорту, а оттуда распределяется
по главным артериям, затем по
более мелким и в конце
концов расходится по миллионам мелких капилляров. По венам кровь
возвращается в сердце. (Один цикл движения крови длится в среднем 20 с.
За сутки сердце перегоняет по всем сосудам до 10 000 л крови!) Скорость
кровотока в разных сосудах различна. Ориентировочные значения этой
скорости представлены в табл. 7.1.
Таблица 7.1. Скорость и давление крови в различных сосудах
На
первый взгляд кажется, что приведенные значения противоречат уравнению
неразрывности – в тонких капиллярах скорость кровотока примерно в 1000
меньше, чем в артериях. Однако это несоответствие кажущееся. Дело в том,
что в табл. 7.1 приведен диаметр одного сосуда. Эта величина
действительно уменьшается по мере разветвления. Однако суммарная площадь
разветвления возрастает. Так, суммарная площадь всех капилляров (около
2000 см2) в сотни раз превышает площадь аорты – этим и
объясняется такая малая скорость крови в капиллярах. Малая скорость
кровотока в капиллярах необходима для обеспечения эффективного обмена
между кровью и тканями.
7.2. Уравнение Бернулли
Для
идеальной жидкости (сила трения полностью отсутствует) справедливо
уравнение, которое было получено швейцарским математиком и физиком
Даниилом Бернулли (1700-1782). Рассмотрим тонкую трубку тока и выделим в
ней два произвольных сечения (рис. 7.2).
Рис. 7.2. Параметры сечений в трубке тока
В общем случае эти сечения находятся на различных высотах (h1 и h2), а их площади различны (S1 и S2). Вследствие уравнения неразрывности различны будут и скорости течения жидкости в этих сечениях (v1и v2). Обозначим давления жидкости в этих сечениях Р1 и Р2 соответственно.
Используя закон сохранения механической энергии, можно доказать, что для этих сечений выполняется следующее соотношение:
Давление Р называют статическим. Это
давление, которое оказывают друг на друга соседние слои жидкости. Его
можно измерить манометром, который движется вместе с жидкостью. Величину
ρv2/2 называют динамическим давлением. Оно обусловлено движением жидкости. Гидростатическое давление ρgh – это давление, создаваемое весом вертикального столба жидкости высотой h.
Уравнение Бернулли формулируется следующим образом:
При
стационарном течении идеальной жидкости полное давление, равное сумме
статического, динамического и гидростатического давлений, одинаково во
всех поперечных сечениях трубки тока.
7.3. Следствия уравнения Бернулли
Горизонтальная трубка тока переменного сечения
При этом h1 = h2 и уравнение (7.3.) принимает вид
Отсюда
следует, что статическое давление идеальной жидкости при течении по
горизонтальной трубке возрастает там, где скорость ее уменьшается, и
наоборот. Это можно продемонстрировать с помощью манометрических трубок,
уровень поднятия жидкости в которых пропорционален статическому
давлению (рис. 7.3). Видно, что в широком сечении (а), где скорость
течения меньше, статическое давление больше, чем в узком сечении (б).
Наклонная трубка тока постоянного сечения
В такой трубке скорость жидкости везде одинакова (v = const), и уравнение (7.3) принимает вид
Следовательно,
скорость истечения струи равна скорости тела при свободном падении с
высоты h. Соотношение (7.9) – это формула Торричелли.
Рис. 7.3. Горизонтальная трубка переменного сечения
Рис. 7.4. Наклонная труба постоянного сечения
Рис. 7.5. Линия тока при истечении жидкости из небольшого отверстия широкого сосуда
Измерение скорости жидкости
Установим
в разных местах горизонтальной цилиндрической трубы (струи жидкости)
одного сечения две трубки: 1) манометрическую трубку, плоскость
отверстия которой расположена параллельно движению жидкости; 2) трубку,
изогнутую под прямым углом навстречу движению жидкости (трубку Пито)
(рис. 7.6).
В движущемся потоке жидкость в трубках
поднимается на разную высоту. Давление под манометрической трубкой равно
статическому давлению Р. Оно уравновешивается давлением атмосферы Ра и давлением столба жидкости h2:
Имея систему двух таких трубок, вычисляют скорость потока жидкости по формуле (7.10).
Рис. 7.6. Измерение скорости жидкости
7.4. Принцип работы инжектора, ингалятора
В
медицине широкое применение находят приборы, действие которых основано
на использовании законов гидродинамики. Рассмотрим два таких прибора.
Инжектор
Этот
прибор используют для дозированной подачи пациенту газообразного
препарата. Например, закиси азота или кислорода. Препарат из баллона
поступает в смесительную камеру через узкое сопло (рис. 7.7).
При
этом скорость движения препарата возрастает, а его давление, в
соответствии с уравнением Бернулли, падает. В смесительной камере
возникает разрежение, и в нее засасывается атмосферный воздух.
Всасывание происходит через одно из отверстий поворотного диска.
Отверстия имеют различные диаметры. Выбирая соответствующее отверстие,
регулируют состав смеси, подаваемой пациенту.
Рис. 7.7. Подача кислорода при кислородной терапии
Ингалятор
Этот прибор используют для введения в область носоглотки лекарственных средств в распыленном виде (рис. 7.8).
Рис. 7.8. Схема ингалятора
Он состоит из двух трубок, расположенных под прямым углом.
Горизонтально
расположенная трубка (1) имеет на конце сужение. Чуть ниже этого конца
располагается верхний конец вертикальной трубки (2), нижний конец
которой опущен в сосуд с жидким препаратом. В горизонтальную трубку
подается пар (3). При прохождении суженного конца скорость пара
возрастает, а давление падает. В область пониженного давления
засасывается препарат, который распыляется струей пара. В результате
образуется смесь пара, воздуха и капелек препарата, которая через
патрубок (4) поступает к пациенту.
7.5. Основные понятия и формулы
Продолжение таблицы
7.6. Задачи
2. Кровь
течет по горизонтальному участку артерии, имеющему сужение. Где
давление крови на стенки сосуда будет больше – на суженном или широком
участке? Динамическим или статическим давлением обусловлено
фонтанирование крови при надрезе артерии?
Решение
Фонтанирование крови при надрезе артерии обусловлено разностью между статическим давлением в артерии и давлением атмосферы.
При
прохождении места сужения скорость кровотока возрастает (7.2), а
статическое давление, которое и воздействует на стенки сосуда,
уменьшается (7.5). Отметим, что вклад динамического давления в полное
давление ничтожен. Действительно, принимая v = 0,5 м/с, ρ = 103 кг/м3, найдем:
Ответ: давление
на стенки незначительно уменьшается на участке сужения артерии.
Фонтанирование крови при надрезе артерии обусловлено статическим
давлением.
3. Скорость потока крови в капиллярах равна примерно v1= 30 мм/мин, а скорость потока крови в аорте v2= 45 см/с. Определить, во сколько раз площадь сечения всех капилляров больше сечения аорты.
4. Лекарственный раствор вводят в мышцу животного с помощью шприца, внутренний диаметр которого d1 = 10 мм, а диаметр иглы d2 = 0,5 мм. Определить скорость истечения раствора из иглы, если скорость перемещения поршня шприца равна v1 = 2,3 см/с.
7. Наблюдая под микроскопом эритроциты в капилляре, можно измерить скорость течения крови: v1= 0,5 мм/с. Средняя скорость тока крови в аорте составляет v2=
40 см/с. На основании этих данных определить, во сколько раз суммарная
площадь поперечных сечений функционирующих капилляров больше площади
сечения аорты.
Решение
Условие
неразрывности струи было получено для трубки тока переменного сечения.
Очевидно, что оно применимо и к разветвлению труб. В задаче такое
разветвление начинается с аорты (площадь поперечного сечения S2) и заканчивается капиллярами (общая площадь сечения S1). Исходя из этого запишем уравнение неразрывности струи (7.2): S1/S2 = v2/v1= 800.
Ответ: 800.
8. При
всасывании человек может понизить давление в легких на 80 мм рт.ст.
ниже атмосферного. Определить, на какую высоту ему удастся втянуть воду
по трубочке.
10. Во время бури или смерча с домов иногда срывает крыши. Используя уравнение Бернулли, объяснить, почему это происходит. Решение
Давление в потоке ветра уменьшается. Поэтому давление на чердаке превышает внешнее давление на величину ΔΡ = pv2/2. При этом на кровлю действует направленная наружу сила F = Spv2/2. При скорости v = 35 м/с (ураган), ρ = 1,3 кг/м3 и S = 100 м2 величина силы составляет F = 61 000 Н (6 т), что существенно превышает вес кровли.
Источник
Очень часто к нам обращаются люди, которые хотят купить вакуумный насос, но слабо представляют, что такое вакуум.
Попытаемся разобраться, что же это такое.
По определению, вакуум – это пространство, свободное от вещества (от латинского слова «vacuus» – пустой).
Существует несколько определений вакуума: технический вакуум, физический вакуум, космический вакуум и т.д.
Мы будем рассматривать технический вакуум, который определяется как сильно разреженный газ.
Рассмотрим на примере, что такое вакуум и как его измеряют.
На нашей планете существует атмосферное давление, принятое за единицу (одна атмосфера). Оно меняется в зависимости от погоды, высоты на уровнем моря, но мы не будем принимать это во внимание, так как это не будет никак влиять на понимание понятия вакуум.
Итак, мы имеем давление на поверхности земли равное 1 атмосфере. Всё, что ниже 1 атмосферы (в закрытом сосуде), называется техническим вакуумом.
Возьмём некий сосуд и закроем его герметичной крышкой. Давление в сосуде будет равно 1 атмосфере. Если мы начнём откачивать из сосуда воздух, то в нём возникнет разряжение, которое и называется вакуумом.
Рассмотрим на примере: в левом сосуде 10 кружочков. Пусть это будет 1 атмосфера.
«откачаем» половину – получим 0,5 атм, оставим один – получим 0,1 атм.
Так как в сосуде всего одна атмосфера, то и максимально возможный вакуум мы можем получить (теоретически) ноль атмосфер.
“Теоретически” – т.к. выловить все молекулы воздуха из сосуда практически невозможно.
По этому, в любом сосуде, из которого откачали воздух (газ) всегда остается какое-то его минимальное количество. Это и называют “остаточным давлением”, то есть давление, которое осталось в сосуде после откачки из него газов.
Существуют специальные насосы, которые могут достичь глубокого вакуума до 0,00001 Па, но всё равно не до нуля.
В обычной жизни редко когда требуется вакуум глубже 0,5 – 10 Па (0,00005-0,0001 атм).
Есть несколько вариантов измерения вакуума, которые зависят от выбора точки отсчёта:
1. За единицу принимается атмосферное давление. Всё, что ниже единицы – вакуум.
То есть шкала вакуумметра от 1 до 0 атм (1…0,9…0,8…0,7…..0,2…0,1….0).
2. За ноль принимается атмосферное давление. То есть вакуум – все отрицательные числа меньше 0 и до -1.
То есть шкала вакуумметра от 0 до -1 (0, -0,1…-0,2….,-0,9,…-1).
Также шкалы могут быть в кПа, mBar, но это всё аналогично шкалам в атмосферах.
На картинке показаны вакуумметры с различными шкалами, которые показывают одинаковый вакуум:
Из всего сказанного выше видно, что величина вакуума не может быть больше атмосферного давления.
К нам почти каждый день обращаются люди, которые хотят получить вакуум -2, -3 атм и т.д.
И они очень удивляются когда узнают, что это невозможно (кстати, каждый второй из них говорит, что “вы сами ничего не знаете”, “а у соседа так” и т.д. и.т.п.)
На самом деле, все эти люди хотят формовать детали под вакуумом, но чтобы прижим детали был более 1 кг/см2 (1 атмосферы).
Этого можно достичь, если накрыть изделие плёнкой, откачать из под неё воздух (в этом случае, в зависимости от созданного вакуума, максимальный прижим составит 1 кг/см2 (1 атм=1 кг/см2)), и после этого поместить это всё в автоклав, в котором будет создано избыточное давление. То есть для создания прижима в 2 кг/см2, достаточно создать в автоклаве избыточное давление в 1 атм.
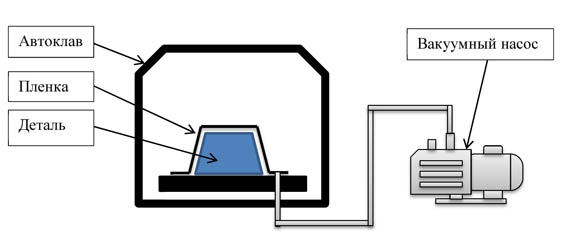
Теперь несколько слов о том, как многие клиенты измеряют вакуум на выставке ООО “Насосы Ампика”, у нас в офисе:
включают насос, прикладывают палец (ладонь) к всасывающему отверстию вакуумного насоса и сразу делают вывод о величине вакуума.
Обычно, все очень любят сравнивать советский вакуумный насос 2НВР-5ДМ и предлагаемый нами его аналог VE-2100.
После такой проверки, всегда говорят одно и тоже – вакуум у 2НВР-5ДМ выше (хотя на самом деле оба насоса выдают одинаковые параметры по вакууму).
В чем же причина такой реакции? А как всегда – в отсутствии знаний законов физики и что такое давление вообще.
Немного ликбеза: давление «P» – это сила, которая действует на некоторую площадь поверхности, направленная перпендикулярно этой поверхности (отношение силы «F» к площади поверхности «S»), то есть P=F/S.
По-простому – это сила, распределённая по площади поверхности.
Из этой формулы видно, что чем больше площадь поверхности, тем меньше будет давление. А также сила, которая потребуется для отрыва руки или пальца от входного отверстия насоса, прямо пропорциональна величине площади поверхности (F=P*S).
Диаметр всасывающего отверстия у вакуумного насоса 2НВР-5ДМ – 25 мм (площадь поверхности 78,5 мм2).
Диаметр всасывающего отверстия у вакуумного насоса VE-2100 – 6 мм (площадь поверхности 18,8 мм2).
То есть для отрыва руки от отверстия диаметром 25 мм, требуется сила в 4,2 раза большая, чем для диаметра отверстия 6 мм (при одинаковом давлении).
Именно по этому, когда вакуум измеряют пальцами, получается такой парадокс.
Давление «P», в этом случае, рассчитывается как разница между атмосферным давлением и остаточным давлением в сосуде (то есть вакуумом в насосе).
Как посчитать силу прижима какой-либо детали к поверхности?
Очень просто. Можно воспользоваться формулой приведенной выше, но попробуем объяснить попроще.
Например, пусть требуется узнать, с какой силой может быть прижата деталь размером 10х10 см при создании под ней вакуума насосом ВВН 1-0,75.
Берём остаточное давление, которое создаёт этот вакуумный насос серии ВВН.
Конкретно у этого водокольцевого насоса ВВН 1-0,75 оно составляет 0,4 атм.
1 атмосфера равна 1 кг/см2.
Площадь поверхности детали – 100 см2 (10см х10 см).
То есть, если создать максимальный вакуум (то есть давление на деталь будет 1 атм), то деталь прижмётся с силой 100 кг.
Так как у нас вакуум 0,4 атм, то прижим составит 0,4х100=40 кг.
Но это в теории, при идеальных условиях, если не будет подсоса воздуха и т.п.
Реально нужно это учитывать и прижим будет на 20…40% меньше в зависимости от типа поверхности, скорости откачки, и т.п.
Теперь пару слов о механических вакуумметрах.
Эти устройства показывают остаточное давление в пределах 0,05…1 атм.
То есть он не покажет более глубокого вакуума (будет всегда показывать «0»). Например, в любом пластинчато-роторном вакуумном насосе, по достижении его максимального вакуума, механический вакуумметр всегда будет показывать «0». Если требуется визуальное отображение значений остаточного давления, то нужно ставить электронный вакуумметр, например VG-64.
Часто к нам приходят клиенты, которые формуют детали под вакуумом (например, детали из композиционных материалов: углепластика, стеклопластика и т.п.), это нужно для того, чтобы во время формовки из связующего вещества (смолы) выходил газ и тем самым улучшались свойства готового продукта, а так же деталь прижималась к форме плёнкой, из-под которой откачивают воздух.
Встаёт вопрос: каким вакуумным насосом пользоваться – одноступенчатым или двухступенчатым?
Обычно думают, что раз вакуум у двухступенчатого выше, то и детали получаться лучше.
Вакуум у одноступенчатого насоса 20 Па, у двухступенчатого 2 Па. Кажется, что раз разница в давлении в 10 раз, то и прижиматься деталь будет гораздо сильнее.
Но так ли это на самом деле?
1 атм = 100000 Па = 1 кг/см2.
Значит разница в прижиме плёнки при вакууме 20 Па и 2 Па составит 0,00018 кг/см2 (кому не лень – посчитает сам).
То есть, практически, разницы никакой не будет, т.к. выигрыш в 0,18 г в силе прижима погоды не сделает.
Расчет времени вакуумирования емкости
Как рассчитать за какое время вакуумный насос откачает вакуумную камеру?
В отличии от жидкостей, газы занимают весь имеющийся объем и если вакуумный насос откачал половину воздуха, находящегося в вакуумной камере, то оставшаяся часть воздуха вновь расширится и займет весь объем.
Ниже приведена формула для вычисления этого параметра.
t = (V/S)*ln(p1/p2)*F, где
t – время (в часах) необходимое для откачки вакуумного объема от давления p1 до давления p2
V – объем откачиваемой емкости, м3
S – быстрота действия вакуумного насоса, м3/час
p1 – начальное давление в откачиваемой емкости, мбар
p2 – конечное давление в откачиваемой емкости, мбар
ln – натуральный логарифм
F – поправочный коэффициент, зависит от конечного давления в емкости p2:
– p2 от 1000 до 250 мбар F=1
– p2 от 250 до 100 мбар F=1,5
– p2 от 100 до 50 мбар F=1,75
– p2 от 50 до 20 мбар F=2
– p2 от 20 до 5 мбар F=2,5
– p2 от 5 до 1 мбар F=3
В двух словах, это всё.
Надеемся, что кому-нибудь эта информация поможет сделать правильный выбор вакуумного оборудования и блеснуть знаниями за кружкой пива…
Источник