Чтобы вычислить давление газа на стенки сосуда надо знать

Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
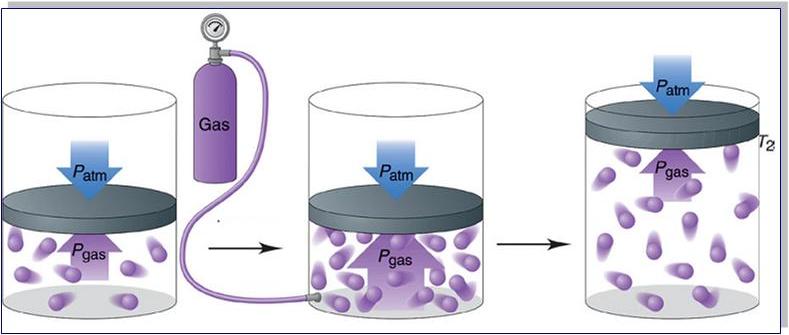
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

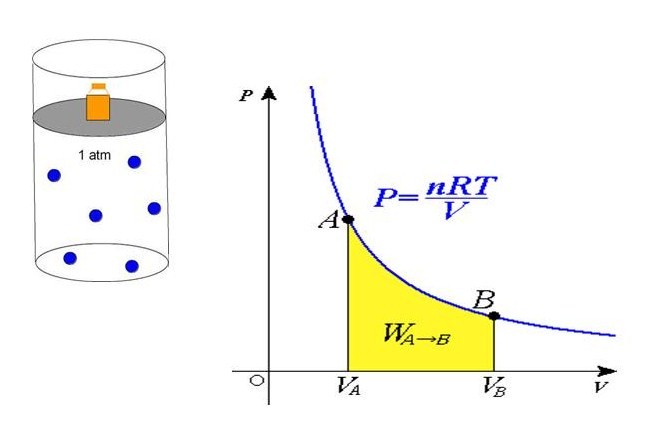
В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Давление газа на стенки сосуда. Закон Дальтона
Давление газа на стенки сосуда
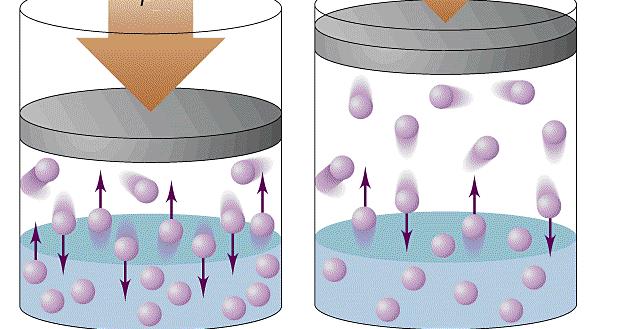
Вследствие теплового движения частицы газа время от времени ударяются о стенки сосуда (рис.1,а). При каждом ударе молекулы действуют на стенку сосуда с некоторой силой. Складываясь друг другом, силы ударов отдельных частиц, образуют некоторую силу давления, постоянно действующую на стенку сосуда. Молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда (рис.1,б).
Рис.1. Давление газа на стенку сосуда: а) возникновение давления вследствие ударов о стенку хаотически движущихся частиц; б) сила давления как результат упругого удара частиц.
На практике чаще всего имеют дело не с чистым газом, а со смесью газов. Например, атмосферный воздух представляет собой смесь азота, кислорода, углекислого газа, водорода и других газов. Каждый из газов, входящих в состав смеси, вносит свой вклад в суммарное давление, которое оказывает смесь газов на стенки сосуда.
Закон Дальтона для газовой смеси
Для газовой смеси справедлив закон Дальтона:
давление газовой смеси равно сумме парциальных давлений каждого компонента смеси:
Рис.2. Закон Дальтона для газовой смеси
С точки зрения молекулярно-кинетической теории закон Дальтона выполняется потому, что взаимодействие между молекулами идеального газа пренебрежимо мало. Поэтому каждый газ оказывает на стенку сосуда давление, как если бы остальных газов в сосуде не было.
Источник
Давление газа — формула. Формула давления газа в сосуде
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 10 23 ), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния
В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
Объем сосуда в кубических метрах равен 0,01 м 3 . Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Давление в жидкости и газе. Расчет давления жидкости на дно и стенки сосуда
Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.
405. Поднимающиеся со дна водоема пузырьки воздуха увеличиваются в объеме по мере приближения к поверхности. Почему?
С приближением к поверхности, давление воды на пузырек падает.
406. Воду из узкого высокого стакана перелили в широкую кастрюлю. Как изменилось давление воды на дно?
Давление уменьшилось, поскольку уменьшилась высота водяного столба.
407. На рисунке 44 изображен старинный опыт: в крышку бочки, наполненную доверху водой, была вставлена высокая узкая трубка. Когда в трубку налили воды, бочка разорвалась. Объясните, почему небольшое количество воды, которую пришлось налить в трубку, могло разорвать бочку?
Давление на стенки бочки будет зависеть от плотности жидкости и высоты водяного столба и не зависит от площади поперечного сечения сосуда.
408. В сосуд налили слой воды высотой 15 см. каково давление этого слоя на дно сосуда?
409. Чему равно давление воды на глубине 50 см?
410. Банка высотой 50 см наполнена водою. Определите давление на 1 см2 дна банки.
411. В мензурку, площадь дна которой 20 см2 , налита вода до высоты 10 см. сколько граммов воды налито? Чему равно давление воды на дно мензурки?
412. Высота уровня воды в водопроводе 10 м (рис.45). Одинаковы ли давления на стенки трубы на различных высотах? Каково давление воды у нижнего конца трубы?
413. Каково давление на дверцу в шлюзовых воротах на глубине 12 м (рис. 46)?
414. В стакан высотой 10 см налита доверху ртуть. Вычислить давление на дно стакана.
415. Вычислите давление столбика ртути высотой 76 см.
416. Поршневой насос может произвести давление 5·105 Па. На какую высоту можно поднять воду этим насосом?
417. В трех сосудах налита вода до одной и той же высоты (рис. 47). В каком сосуде налито больше воды? В каком сосуде больше давление на дно?
Давление во всех сосудах на дно одинаково.
418. Внутрь жидкости погружен брусок (рис 48). Одинаковые ли давления испытывают боковые стенки бруска (левая и правая, передняя и задняя)? Одинаковые ли давления испытывают верхняя и нижняя грани бруска?
Боковые стенки испытывают одинаковое давление; верхняя и нижняя – разное.
419. Рассмотрите рисунок 48. Высота погруженного бруска АК=5 см. На сколько больше давление на грани MNKL, чем на ABCD, если брусок помещен в воду на глубину 12 см (до нижней грани)?
420. Если в подводной части судна появилась пробоина, то на эту пробоину накладывают «пластырь» — кусок паруса, который давлением воды прижимается к корпусу судна и не пропускает в пробоину воду. Определите силу, с которой прижимается пластырь, если площадь пробоины 0,5 м2 , а глубина, на которой сделана пробоина , 2 м.
421. В сталелитейном производстве «изложницей» называется чугунный стакан без дна, в который выливают Расплавленный металл (рис. 49). Верхнее отверстие изложницы немного меньше нижнего для того, чтобы можно было изложницу снять с отвердевшего слитка, когда остынет металл. Чтобы металл снизу не выливался, изложницы ставят на плоское основание и делают их очень массивными. На рисунке 49 слева изображена изложница, справа — подъем изложницы с отлитого слитка.
Определите силу давления, которую производит на подложку изложницы налитый чугун, если высота изложницы 1,5 м, а площадь нижнего основания 1600 см2. Плотность чугуна 7,2 г/см3.
422. Для спуска водолаза на очень большую глубину применяется специальный металлический скафандр (рис . 50). Какую силу давления должен выдержать этот скафандр на глубине 300 м, если общая поверхность скафандра составляет 2,5 м2 ?
423. Для выпуска расплавленного металла из литейного ковша делают на дне ковша отверстие, закрываемое специальной пробкой из огнеупорного металла. Определите давление расплавленной стали на пробку, если высота налитого металла 2 м, а плотность расплавленной стали 7,3 г/см³.
424. Как велика должна быть высота столба ртути и столба спирта, если этот столб производит давление в 105 Па?
425. Определите давление воды на стенки котла водяного отопления, если высота труб 20 м?
426.Вычислите разность давлений в трубах водопровода на нижнем этаже здания и на этаже, расположенном выше на 15 м?
427. Батискаф спустился в море на глубину в 50 м. Каково давление на поверхность батискафа на данной глубине?
428. Давление в водопроводе 4·105 Па. С какой силой давит вода на пробку, закрывающую отверстие трубы, если площадь отверстия 4 см2 ?
429. Давление в трубах водопровода 4·105 Па. На какую высоту будет бить вода из пожарной трубы, присоединенной к этому водопроводу, если не принимать во внимание сопротивление воздуха и трение воды в трубах?
430. Человек стоит на кожаном мешке с водой (рис. 51). Рассчитайте, на какую высоту поднимается вода в трубке, если масса человека 75 кг, площадь соприкасающаяся с мешком поверхности платформы 1000 см2.
Источник
Источник
