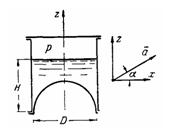
Цилиндрический сосуд заполнен водой на высоту
Часть 4-1 Равновесие жидкости в движущихся сосудах
Задача (Куколевский И.И.) 4-1. Для измерения ускорения горизонтально движущегося тела может быть использована закрепленная на нем U-образная трубка малого диаметра, наполненная жидкостью. С каким ускорением движется тело, если при движении установилась разность уровней жидкости в ветвях трубки, равная h = 5 см при расстоянии между ними l = 30 см?
Ответ. а = 1,635 м/с2.
Скачать решение задачи 4-1 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-2. Призматический сосуд длиной 3*l = 3 м и шириной с = 1 м, перемещающийся горизонтально с постоянным ускорением а =0,4g, разделен на два отсека, заполненных водой до высот h1 = 1 м и h2 = 1,75л.
1) Определить cуммарную силу давления P воды на перегородку.
2) Найти ускорение, при котором эта сила станет равной нулю.
Ответ. 1) Р = 2,17 кН.2) а = 0,5g.
Скачать решение задачи 4-2 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-3. Цистерна диаметром D = 1,2 м и длиной L = 2,5 м, наполненная нефтью (δ = 0,9) до высоты b = 1 л, движется горизонтально с постоянным ускорением а = 2 м/с2.
1) Определить силы давления на плоские боковые крышки А и В цистерны.
2) Как изменятся эти силы при замене плоских крышек сферическими. Увеличение объема цистерны при такой замене равно 2W, где W = 0,2 м3.
Ответ 1) PА = 7,42 кН. РB = 12,5 кН; 2) Р’А = 7,3 кН; Р’В = 13 кН.
Скачать решение задачи 4-3 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-4. По наклоненной под углом а = 45° к горизонту плоскости под действием силы тяжести скользит призматический сосуд, целиком заполненный водой. Сосуд закрыт крышкой с малым отверстием, расположенным на расстоянии l = 0,5 м от передней стенки. Собственный вес сосуда G=150 кГ, размер b=1 м, коэффициент трения дна сосуда о плоскость скольжения f= 0,278. Найти величины сил давления воды на крышку 1, стенки 2 и 3, дно 4, считая, что жидкость из сосуда не выливается.
Ответ. P1=0 Р2=4,9 кН; P3 = 8,98 кН; Р4 =13,3 кН.
Скачать решение задачи 4-4 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-5. Составной цилиндрический сосуд, заполненный водой до высоты h1+h2 = 800 мм, подвешен на шнуре, перекинутом через блоки, и соединен с грузом массой m = 200 кг. Определить нагрузки болтовых групп А, В и С при имеющем место ускоренном движении сосуда. Размеры сосуда D1 = 400 мм, D2=600 мм, h1 = 300 мм. Собственным весом сосуда и трением в блоках пренебречь.
Ответ. РА1= 1,67 кН; РВ = PС= 2,56 кН.
Скачать решение задачи 4-5 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-6. Цилиндрический сосуд диаметром d = 0,8 м, имеющий плоскую крышку и полусферическое дно, заполнен водой до высоты у =0,3 ми поднимается вертикально вверх с ускорением а =10 м/с2.
1) Определить усилие Т в тяге, если вес дна сосуда m1 = 50 кк, цилиндрической части m2 = 30 кг и крышки m3 = 20 кu.
2) Силу давления на дно сосуда, если вакуумметр, присоединенный к нижней точке сосуда, показывал V = 30 кПа, когда сосуд был неподвижен.
3) Построить эпюру давления жидкости по высоте в неподвижном сосуде и при ускоренном его движении.
Ответ. 1) Т = 7,63 кН. 2) P = 12,9 кН.
Скачать решение задачи 4-6 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-7. Вычислить величины горизонтальной и вертикальной сил давления на полусфгрическую крышку цилиндрического сосуда диаметром D = 0,6 м, скользящего с ускорением а = 5 м/с2 по плоскости, наклоненной под углом а = 60° к горизонту, если сосуд заполнен водой до уровня h=1 м в открытой трубке, присоединенной к верхней точке сосуда. Как изменятся эти силы, если сосуд остановить?
Ответ. Рв = 1700Н, Рг = 141 Н. Для неподвижного сосуда Рв = 3050 Н; Рг=0
Скачать решение задачи 4-7 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-8. Закрытый цилиндрический сосуд диаметром D = 0,6 м, имеющий полусферическое дно, наполнен до уровня H = 0,8 м водой и движется прямолинейно под углом а = 30° к горизонту с постоянным ускорением а = 2g. Определить вертикальную и горизонтальную силы давления на дно, если избыточное давление газа лад поверхностью воды в сосуде Рн = 20 кПа.
Ответ. Рв = 8980 Н; Рг = 960 Н.
Скачать решение задачи 4-8 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-9. Найти зависимость показания h водяного манометра (радиусы ветвей R1 и R2 заданы), присоединенного к замкнутому сосуду, который наполнен газом, находящимся под вакуумом Pв, от: 1) поступательного ускорения сосуда (а), направленного по вертикали вверх и вниз; 2) угловой скорости вращения сосуда (w).
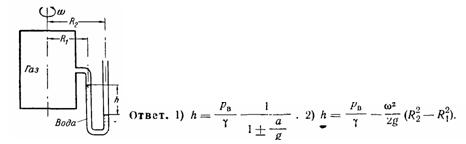
Скачать решение задачи 4-9 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-10. Цилиндрический сосуд, заполненный водой, приведен во вращение с постоянной угловой скоростью w = 10 рад/с. Найти наименьшее давление в воде, заполняющей сосуд, по показанию h= 1 м ртутного манометра, вращающегося вместе с сосудом, если r1 = 0,8 м; r2 = 0,7 м. При какой угловой скорости равновесие жидкости в сосуде нарушится?
Ответ. 1) р=3 кПа. 2) w=13,2 рад/с.
Скачать решение задачи 4-10 (Куколевский И.И.) (цена 80р)
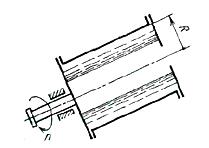
Задача (Куколевский И.И.) 4-11. Вал жидкостного тахометра вращает диск, который увлекает во вращательное движение масло, находящееся в нижней полости корпуса прибора, куда оно поступает из верхней полости через радиальные отверстия полого вала. Создающееся в нижней полости повышенное за счет вращения давление измеряется пьезометром.
Определить высоту Н шкалы пьезометра, необходимую для измерения числа оборотов вала тахометра n = 300 об/мин, если диаметр диска D = 0,2 м. Влиянием зазора между диском и корпусом прибора пренебречь.
Ответ. H= 0,504 м.
Скачать решение задачи 4-11 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-12. Цилиндрический сосуд с закраиной, имеющий диаметр D = 400 мм и высоту H = 300 мм. предварительно целиком заполненный жидкостью, равномерно вращается относительно вертикальной оси, делая 200 об/мин. Какой объем жидкости может удержаться в сосуде при данном числе оборотов, если диаметр закраины d = 200 мм? Какой наибольший объем жидкости удержится в сосуде при сколь угодно большом числе оборотов?
Ответ W1=34,2л, W2= 28,3 л.
Скачать решение задачи 4-12 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-13. Найти число оборотов цилиндрического сосуда высотой H0 = 1,2 м и диаметром D = 0,8м, наполненного жидкостью до высоты H0/2, при котором жидкость поднимется до краев сосуда. Определить число оборотов сосуда, при котором в нем останется лишь половина первоначального объема жидкости.
Ответ, n1= 116 об/мин. n2 = 163,5 об/мин.
Скачать решение задачи 4-13 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-14. Тормозной шкив диаметром D1 = 800 мм и высотой H0=200 мм, вращающийся относительно вертикальной оси при n=120 об/мин, наполнен охлаждающей водой до предела, соответствующего данному числу оборотов.
1) Определить радиус rх сухой части дна, если D2 = 500 мм.
2) Силы, приложенные к верхнему и нижнему днищам.
3) На какой высоте х установится вода после остановки шкива.
Ответ. 1) rх = 194 мм. 2) Р1= 1180 Н; Р2= 1850 Н. 3) r = 137 мм.
Скачать решение задачи 4-14 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-15. Замкнутый цилиндр размерами R= 0,4 лг и H0 = 0,7 м содержит воду в количестве W = 0,25 м3 и вращается относительно вертикальной оси с угловой скоростью w = 10; 20 и 100 рад/с. Определить усилия, действующие при указанных оборотах на крышку цилиндра, если давление над водой равно атмосферному.
. Ответ. Р = 0,176 кН; 2,9 кН и 100 кН
Скачать решение задачи 4-15 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-16. Цилиндрический сосуд диаметром D = 690 мм и высотой H0 = 500 мм заполнен водой до Н = 400 мм. Остальной объем сосуда заполнен маслом (δ=0,8). Сосуд закрыт крышкой с малым отверстием в центре и приведен во вращение относительно центральной вертикальной оси. Определить, с какой угловой скоростью ш нужно вращать сосуд для того, чтобы поверхность раздела жидкостей коснулась дна сосуда. Найти усилия, действующие при этом на дно и крышку сосуда.
Ответ. w= 16,5 рад/с; Pкр = 1,51 кН; Рдно = 2,84 кН.
Скачать решение задачи 4-16 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-17. Цилиндрический сосуд диаметром D = 1,2 м, наполненный водой до высоты а = 0,6м в пьезометрах одинакового диаметра, установленных на крышке сосуда на расстояниях r1 = 0,2 м и r2 = 0,4 м от оси, вращается с числом оборотов n = 60 об/мин. Определить силу давления на крышку сосуда и указать, как она будет меняться качественно, если поочередно выключать пьезометры.
Ответ. Р = 8450 Н.
Скачать решение задачи 4-17 (Куколевский И.И.) (цена 80р)
Часть 4-2 Равновесие жидкости в движущихся сосудах
Задача (Куколевский И.И.) 4-18. Изображенный на чертеже сосуд имеет размеры D = 0,4 м; d = 0,2 м, b = 0,35 м и наполнен водой до высоты а+b = 0,52 м. Сверху сосуд закрыт поршнем, масса которого m = 50 кг. Определить гидравлические нагрузки болтовых групп А и В, если сосуд вращается относительно центральной вертикальной оси с числом оборотов n = 450 об/мин. Трением между поршнем и стенками цилиндра пренебречь.
Указание. При вращении системы суммарная сила давления жидкости на поршень равна весу поршня. Это условие позволяет найти давление в центре поршня и, следовательно, во всех точках сосуда.
Ответ. РА=РВ = 3710 Н.
Скачать решение задачи 4-18 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-19. Жидкостный тахометр состоит из цилиндра, наполненного ртутью и сообщенного с двумя трубками малого диаметра d, расположенными на расстоянии R от оси. Цилиндр снабжен поршнем, имеющим диаметр D. Поршень перемещается при изменении числа оборотов тахометра. Установить связь между числом оборотов n тахометра и опусканием h поршня от его начального положения при невращающемся тахометре.
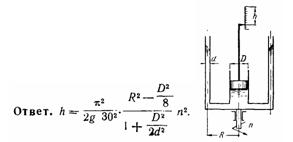
Скачать решение задачи 4-19 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-20. В жидкости, плотность которой ρ, удерживается в равновесии тело плотностью ρ1. Определить, какое начальное ускорение a0, по отношению к жидкости приобретет тело, если его освободить, при условии., что: 1) сосуд, содержащий жидкость, неподвижен; 2) сосуд движется вертикально (вверх или вниз) с постоянным ускорением а; 3) сосуд равномерно вращается относительно вертикальной оси с угловой скоростью w; 4) сосуд движется горизонтально с постоянным ускорением а.
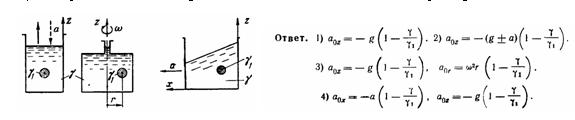
Скачать решение задачи 4-20 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-21. Определить минимальное число оборотов литейной формы, при котором легкие включения имеют возможность выделиться из расплавленного металла в середину формы, при следующих размерах отливаемой детали: D1 = 300 мм; D2 = 200 мм; Н = 300 мм.
Указание. Условия относительного движения легкой частицы во вращающейся литейной форме определяются действием на нее сил давления жидкого металла Р, собственного веса частицы G и переносной силы инерции J. Направление результирующей К этих сил обеспечивает при любом числе оборотов перемещение легких включений по внутреннему наклонному и горизонтальному каналам формы к ее центру. По внешнему наклонному каналу (см. рис. к задаче 4-21) легкие включения могут перемещаться к центру формы лишь в том случае, когда результирующая R имеет составляющую, направленную вдоль стенки вниз.
Ответ, n = 231 об/мин.
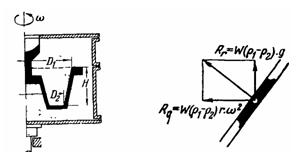
Скачать решение задачи 4-21 (Куколевский И.И.) (цена 80р)
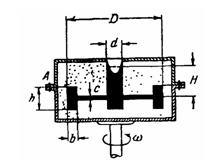
Задача (Куколевский И.И.) 4.22 Отливка чугунного колеса диаметром D = 1000 мм, с ободом высотой h = 200 мм и толщиной d = 80 мм, диском толщиной с = 40 мм и ступицей диаметром d = 200 мм производится во вращающуюся с n = 200 об/мин земляную форму. Определить растягивающую силу в болтовой группе А опоки, не учитывая веса опоки и земли. Высота заполнения формы Н = 300 мм, плотность жидкого чугуна у = 7200 кг/м3.
Ответ. РА = 167 кН.
Задача (Куколевский И.И.) 4-23. Определить силу давления на коническую боковую поверхность АВС и плоское дно АС сосуда, целиком заполненного водой и вращающегося с угловой скоростью wо = 20 рад/с, если известно, что в верхней точке В сосуда вакуум равен рв = 20 кПа. Размеры сосуда: D=1 м; а = 1 м.
Ответ. РАВС = 9,38 кН; РАС = I 2 кН.
Скачать решение задачи 4-23 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-24. Определить наименьшее число оборотов, при котором полностью опорожнится предварительно заполненный жидкостью Открытый конический сосуд, имеющий диаметры D1 = 460 мм; D2 = 200 мм и высоту H0 = 75 мм. Указание. Полное опорожнение сосуда произойдет при таком числе оборотов, когда свободная поверхность жидкости коснется стенки сосуда у его дна и вектор суммарной массовой силы, действующей на последнюю частицу жидкости в этой точке, окажется нормальным к стенке.
Ответ. n = 71,7 об /мин.
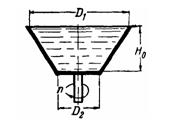
Задача (Куколевский И.И.) 4-25. Сосуд, вращающийся относительно вертикальной оси, состоит из двух цилиндров одинаковой высоты а = 200 мм и диаметров d=150 мм. и D = 300 мм. Нижний цилиндр целиком заполнен жидкостью. При каком числе оборотов жидкость начнет выливаться из сосуда? Отметить качественное влияние размеров а, d и D сосуда на искомое число оборотов.
Ответ, n = 252 об /мин.
Скачать решение задачи 4-25 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-26. Цилиндрический сосуд радиуса R = 250 мм и высоты h1 = 300 мм, заполненный объемом жидкости W = 45 дм3, вращается относительно центральной вертикальной оси. Ко дну сосуда присоединена изогнутая трубка, ось нижнего конца которой совпадает с осью вращения сосуда. Конец трубки опущен под уровень неподвижной жидкости, расположенный ниже дна верхнего сосуда на h2 = 460 мм.
1) Определить угловую скорость w* вращения сосуда, при которой жидкость во вращающейся трубке находится в относительном покое.
2) Выяснить направление движения жидкости в трубке при w>< w*. Указание. Относительный покой жидкости в трубке возможен только при условии, что давление в точке а трубки на уровне свободной поверхности в неподвижном сосуде равно атмосферному и что, следовательно, вершина параболоида пьезометрической поверхности проходит через эту точку
Ответ, w*=30 рад/с
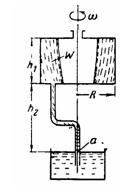
Задача (Куколевский И.И.) 4-27. Гидравлическая пята, вращающаяся с числом оборотов n = 3000 об/мин, получает воду по трубке А под давлением р= 10 атм. Определить осевую силу Р, которую может уравновешивать пята, считая, что вода под поршнем вращается с половиной угловой скорости вращения последнего. Диаметр поршня D = 0,32 м, диаметр вала d = 0,05 м, трубка присоединена к корпусу пяты на расстоянии а = 0,07 м от оси. На каком расстоянии от оси нужно расположить трубку А, чтобы осевая сила, уравновешиваемая пятой, не зависела от оборотов?
Ответ. Р = 86 кН, а =0,113 м.
Скачать решение задачи 4-27 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-28. Определить диаметр D1 на котором установится вода во внутренней полости гидравлического уплотнения вала воздушной машины, если диаметр вала d = 0,15 м, диаметр, на котором установилась вода в наружной полости уплотнения, D = 0,3 м и вакуум во внутренней полости Pв = 0,7 ат. Вал вращается с числом оборотов n = 2000 об/мин, а угловая скорость вращения воды равна половине угловой скорости вращения вала. Определить осевое усилие, передаваемое на вал диском уплотнения.
Ответ. D1 = 20 см; Р = 2,3 кН.
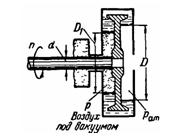
Скачать решение задачи 4-28 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4-29. Замкнутый цилиндрический сосуд размерами D = 400 мм и L = 400 мм, вращающийся с числом оборотов n = 3000 об/мин, заполнен равными объемами воды и бензина (δ = 0,7), образующими слои одинаковой высоты h = 150 мм. 1) Определить, пренебрегая весомостью жидкости наибольшее давление в сосуде. 2) Растягивающие усилия Р1 и P2 в осевом сечении сосуда и в сечении, перпендикулярном его оси.
Ответ. 1) ри = 1,25 МПа. 2) P1 = 202 кН; P2= 54 кН.
Скачать решение задачи 4-29 (Куколевский И.И.) (цена 80р)
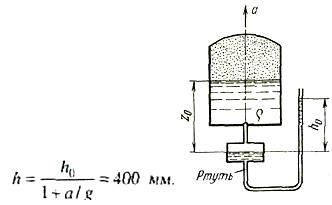
Задача (Куколевский И.И.) 4.30. Показание ртутного чашечного манометра, присоединенного к замкнутому баку, в котором находится жидкость плотностью р = 1500 кг/м3, равно h0 = 800 мм. Как изменится показание манометра, если системе сообщить поступательное ускорение, направленное вверх и равное ускорению свободного падения (a=g)? Изменениями уровня жидкости в баке и ртути в чашке манометра пренебречь (z0 = 1 м); давление газа в баке считать неизменным. Рассмотреть, частный случай, когда ноль шкалы манометра находится на уровне жидкости в баке (z0 = 0).
Ответ. h = 455 мм; при z0 = 0 показание манометра
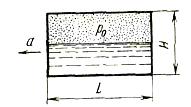
Задача (Куколевский И.И.) 4.31. Закрытый призматический сосуд размерами L*H*C = 3*1*1 м до середины высоты заполнен водой, над уровнем которой имеется избыточное давление газа Po = 50 кПа. Сосуд движется горизонтально с постоянным ускорением а = 0.5*g. Определить силы давления на заднюю стенку (Рз) и дно (Рд) сосуда. Как повлияет на силы давления отсутствие поля сил тяжести?
Ответ. Рз = 57,36 кН и Рд=165.3кН; Рз =57,36кН и Рд=155,5кН.
Задача (Куколевский И.И.) 4.32. Цилиндрический сосуд радиусом R= 100 мм, заполненный водой на 3/4 своего объема, вращается равномерно с частотой n= 10 000 об/мин относительно своей оси. Пренебрегая действием силы тяжести, определить силу давления воды на торцовую стенку сосуда.
Ответ. P = 48,2 кН.
Задача (Куколевский И.И.) 4.33. Определить силу давления воды па полусферическую крышку цилиндрического сосуда радиусом R = 0,2 м, если сосуд вращается относительно своей оси с угловой скоростью w = 100 рад/с и манометр при этом показывает давление М = 50кПа. Действием силы тяжести на жидкость пренебречь.
Ответ. Р=18,8 кН.
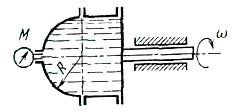
Скачать решение задачи 4-33 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4.34. Конический сосуд размерами d = 0,6 м. D= 1 м, а = 0,9 м заполнен водой и приведен в равномерное вращение с угловой скоростью w = 20 рад/с. Давление в центре крышки сосуда по манометру М = 10 кПа. Определить гидравлические нагрузки болтовых групп А и В сосуда: 1) учитывая действие силы тяжести; 2) пренебрегая действием этой силы.
Ответ. РA = 27,7 кН; 1) PB = 3.34 кН; 2) PB = 5,37 кН.
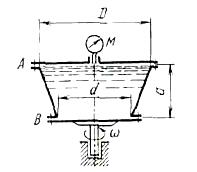
Скачать решение задачи 4-34 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4.35. Цилиндрический сосуд с горловиной, размеры которого d = 0,2 м, D = 0,4 м, а = 0,4 м и b = 0,2 м, равномерно вращается вокруг своей вертикальной оси. Сосуд предварительно заполнен жидкостью (р = 1325 кг/м3) до высоты h = 0,1 м в горловине. Найти угловую скорость со сосуда, при которой из него начнет выливаться жидкость. При этой угловой скорости определить силу давления Р жидкости на крышку К сосуда. Как изменятся сила давления на крышку, если угловая скорость станет вдвое больше найденной?
Ответ, w = 34,3 рад/с; Р = 1600 и 4900 Н.
Скачать решение задачи 4-35 (Куколевский И.И.) (цена 80р)
Задача (Куколевский И.И.) 4.36. Определить силу давления на верхнюю половину шара радиусом R=0,6 м, заполненного водой до уровня h= 1,2 м в пьезометре, в следующих четырех случаях: 1} шар неподвижен; 2) вращается вокруг вертикальной оси с угловой скоростью w = 12 рад/с, 3) свободно падает и поле силы тяжести; 4} свободно падает вращаясь с угловой скорости w=12 рад/с.
Ответ Р = 8,8; 23,5; 0 и 14,7 кН.
Скачать решение задачи 4-36 (Куколевский И.И.) (цена 80р)
Источник
В.Л.БУЛЫНИН,
ЦО № 17 ЦАО, г. Москва
Согласно школьной программе, законы гидростатики изучаются лишь в 7-м классе, возвращение к их изучению и закреплению в дальнейшем не предусмотрено. Тем не менее задачи на гидростатику относятся к весьма трудным и, если в старших классах не было решено достаточно подобных задач, то на вступительных экзаменах в технические вузы ученик может столкнуться с очень серьёзными, а то и непреодолимыми трудностями. Предлагаемая подборка задач имеет своей целью дать школьнику и преподавателю физики представление об уровне сложности материала по этой теме.
Задача 1 (МГТУ им. Н.Э.Баумана). Плотность раствора соли с глубиной меняется по закону = 0 + Ah, где 0 = 1 г/см3, А = 0,01 г/см4. В раствор опущены два шарика, связанные нитью такой длины, что расстояние между центрами шариков не может превышать L = 5 см. Объём каждого шарика V = 1 см3, массы m1 = 1,2 г и m2 = 1,4 г. На какой глубине находится каждый шарик?
Решение.
В силу симметрии шариков относительно горизонтальной плоскости, пороходящей через их центры, сила Архимеда для каждого шарика равна gV, где – плотность жидкости на уровне центра шарика. Запишем условие равновесия для каждого из шариков и сложим уравнения:
где
Объединяя все уравнения, находим:
h2 = h1 + L.
Подставляя числовые данные, получаем:
h1 = 27,5 см; h2 = 32,5 см.
Задача 2 (МГТУ им. Н.Э.Баумана). В водоёме укреплена вертикальная труба с поршнем так, что нижний конец её погружён в воду. Поршень, лежавший вначале на поверхности воды, медленно поднимают на высоту H = 15 м. Какую работу пришлось на это затратить, если площадь поршня 1 дм2, атмосферное давление p0 = 105 Па? Массой поршня пренебречь.
Решение. Сила, которую надо прикладывать к поршню, линейно возрастает от 0 до Fmax = p0S. Зависимость этой силы от высоты столба поднятой воды равна F(h) = ghS, где – плотность воды, h – высота столба поднятой воды, S – площадь поршня.
Максимально возможная высота столба воды, поднятой таким способом, h1 = 10 м, при этом gh1 = p0. График зависимости F = F(h) изображён на рисунке. Очевидно, что работа по подъёму поршня равна площади трапеции под графиком F(h):
Подставив числовые данные, получаем A = 104 Дж.
Задача 3. Льдина площадью 1 м2 и толщиной 0,4 м плавает в воде. Какую минимальную работу надо совершить, чтобы полностью погрузить льдину в воду? Плотность льда 900 кг/м3, g = 10 м/с2.
Решение. Пусть в исходном состоянии h – глубина погружения плавающей льдины. Запишем условие равновесия и следствия из него:
где в, л – плотности воды и льда соответственно, Vпогр – объём погружённой части льдины, V – её полный объём, Н – толщина льдины, h – толщина погружённой части.
При погружении льдины сила нажима линейно возрастает от нуля до Fmax, совершая работу
Задача 4. Бетонная однородная свая массой m лежит на дне водоёма глубиной h, большей, чем длины сваи l. Привязав трос к одному концу сваи, её медленно вытаскивают из воды так, что центр тяжести сваи поднимается на высоту H от поверхности воды (H > l). Какая работа совершается при подъёме сваи? Плотность бетона в n раз больше плотности воды. Силами сопротивления пренебречь.
Решение
1-й способ. Разобьём работу на три этапа:
Подъём верхнего конца сваи до поверхности воды:
– центр тяжести поднимается на высоту
– сила натяжения троса постоянна и равна mg – FA;
– работа (плотность бетона, по условию, в n раз больше плотности воды).
Подъём сваи на высоту l – такую, чтобы нижний конец сваи касался поверхности воды:
– сила натяжения троса линейно возрастает от mg – FA до mg, и работа этой силы равна
Наконец, подъём центра тяжести на высоту H над поверхностью воды:
– сила натяжения троса постоянна и равна mg;
– работа (на высоту центр тяжести уже был поднят на предыдущем этапе).
Общая работа A = A1 + A2 + A3:
2-й способ. Применим закон сохранения энергии. Работа равна изменению энергии системы свая-вода. Потенциальная энергия сваи возросла на mg(H + h). Потенциальная энергия воды уменьшилась на – вода из верхнего слоя водоёма опустилась на дно и заняла объём, прежде занятый сваей. Отсюда:
Задача 5 (МГТУ им. Н.Э.Баумана). В сосуде находятся три несмешивающиеся жидкости плотностями (сверху вниз) , 2 и 3. Толщина этих слоёв Н/3, H и H соответственно. На дне сосуда лежит стержень из материала плотностью 6, массой m, длиной H. Какую работу надо совершить, поднимая стержень за один конец вертикально, чтобы его верхний торец коснулся поверхности жидкости плотностью ? Толщиной стержня пренебречь. Трение отсутствует.
Решение
Пусть V – объём стержня, A1 – работа по подъёму стержня в жидкости плотностью 3 в вертикальное положение (подъём центра масс на высоту H/2):
При перемещении стержня из жидкости плотностью 3 до верхнего уровня жидкости плотностью 2 сила линейно изменяется от При этом центр тяжести стержня перемещается на высоту H. Следовательно, работа равна:
A3 – работа по подъёму части стержня длиной внутри жидкости плотностью 2 (при этом нижний конец стержня и соответственно центр тяжести этой части стержня поднимается на ):
A4 – работа по перемещению части стержня длиной из жидкости плотностью 2 в жидкость плотностью :
Полная работа равна:
A = A1 + A2 + A3 + A4 =
где – масса стержня.
Задача 6. Акселерометр представляет собой изогнутую под прямым углом трубку, заполненную маслом. Трубка располагается в вертикальной плоскости, угол При движении трубки в горизонтальном направлении с ускорением a уровни масла в коленах трубки соответственно равны h1 = 8 см и h2 = 12 см. Найдите величину ускорения a.
Решение
Рассмотрим сосуд с жидкостью (аквариум), который движется в горизонтальном направлении с ускорением a. При таком движении поверхность жидкости составляет угол с горизонтальной плоскостью, такой что
Такой же перепад высот имеет и жидкость в трубке акселерометра, движущегося с тем же ускорением. Получаем l = h2 + h1,
т.к., по условию, = 45°.
Задача 7 (НГУ). Вертикальный цилиндрический сосуд радиусом R, частично заполненный жидкостью, вращается вместе с жидкостью вокруг своей оси.
К боковой стенке сосуда на нити длиной l привязан воздушный шарик радиусом r; во время вращения нить образует со стенкой угол . Найдите угловую скорость вращения сосуда.
Решение
Задача 8 (МГТУ им. Н.Э.Баумана). Цилиндрический сосуд с жидкостью плотностью вращается с постоянной угловой скоростью вокруг вертикальной оси ОО1. Внутри сосуда к оси OO1 в точке A прикреплён тонкий горизонтальный стержень AB, по которому без трения может скользить муфта в виде шара радиусом r. Шар связан с концом A стержня пружиной жёсткостью k, длина которой в нерастянутом состоянии равна L0. Определите расстояние до центра шара от оси вращения, если плотность материала шара в четыре раза меньше плотности жидкости.
Решение
Направим ось X по направлению стержня AB, а ось Y по вертикальной оси OO1. По условию задачи, перемещение шара возможно лишь вдоль стержня. Так как плотность шара меньше плотности жидкости, составляющая силы Архимеда вдоль оси X больше составляющей силы mgэфф, и шар будет вытесняться жидкостью к оси вращения, сжимая пружину. Исходное положение центра шара L0 + r. Пусть во время вращения центр шара находится на расстоянии x от оси, при этом пружина сжата на величину L0 + r – x. Уравнение движения шара массой m по окружности радиусом x с угловой скоростью имеет вид m2x = Fц, где сила Fц – результат сложения горизонтальной составляющей силы Архимеда и силы упругости сжатой пружины: Fупр = k(L0 + r – x).
Если – плотность материала шара, то
Отсюда получаем:
По условию, В итоге получаем ответ:
Задача 9 (НГУ). Цилиндрический космический корабль радиусом R вращается вокруг своей оси с угловой скоростью . Бассейн в корабле имеет глубину H, а дном бассейна служит боковая стенка корабля. Определите плотность плавающей в бассейне палочки длиной l < H, если из воды выступает её верхняя часть длиной .
Решение
Во вращающейся неинерциальной системе отсчёта роль силы тяжести играет центробежная сила инерции Fц = m2r, где r – расстояние элемента массы m от оси вращения. Центр масс погружённой части палочки находится от оси вращения на расстоянии
Сила Архимеда, действующая на погружённую часть палочки длиной l – , равна FA = ж2rц(l – )S, где ж – плотность жидкости (воды), S – площадь поперечного сечения палочки.
Центр масс всей палочки находится от оси вращения на расстоянии
Условие плавания палочки: P = FA, где P – вес палочки.
где – плотность палочки;
Приравняв P и FА, находим плотность палочки:
Вячеслав Леонидович Булынин окончил физический факультет Ленинградского государственного университета в 1964 г. и по 1992 г. работал в научно-исследовательских институтах в области прикладной сверхпроводимости. С 1993 г. преподаёт в школе физику, астрономию, математику; педагогический стаж 15 лет. Учитель высшей квалификационной категории, методист ЦО № 17. Автор двух пособий по физике, изданных «Континентом-Пресс» в 2004 г.: «Физика. Тесты и задачи» и «Физика. Пособие для подготовки к государственному экзамену». Женат, имеет двух дочерей.
Источник
