Давление азота в сосуде

30.10.2020
0
Главная › Сосуды › Давление азота в сосуде
Давление азота в сосуде thumbnail

Äàëåå: 1.2. 
Çàäà÷è äëÿ ñàìîñòîÿòåëüíîãî
Ââåðõ: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è
Íàçàä: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è

1.1.  Ïðèìåðû ðåøåíèÿ
çàäà÷

Ïðèìåð 1.1.  Ñæèæåííûå ãàçû õðàíÿò â ñîñóäàõ,
ñîîáùàþùèõñÿ ñ àòìîñôåðîé. Ìîæíî ëè
äîïóñòèòü èñïàðåíèå æèäêîãî àçîòà îáúåìîì $0,5,{ë}$ è
ïëîòíîñòüþ
$0,81,{ã/ñì}^3$â
çàêðûòîì ñîñóäå îáúåìîì $10,{ë}$ ïðè íàãðåâàíèè
åãî äî òåìïåðàòóðû $20^circ C$, åñëè ñòåíêè ñîñóäà
âûäåðæèâàþò äàâëåíèå
$20,{àòì}$?

hbox to 0.4hsizeÐåøåíèå.
Ïðè ïîâûøåíèè òåìïåðàòóðû æèäêèé àçîò ïåðåéäåò â ãàçîîáðàçíîå
ñîñòîÿíèå.
Ïðèìåì åãî ïðè òåìïåðàòóðå $20^circ C$ çà èäåàëüíûé ãàç è
ïðèìåíèì äëÿ ðåøåíèÿ
óðàâíåíèå Êëàïåéðîíà – Ìåíäåëååâà:

begin{displaymath} PV = {movermu}RT,, end{displaymath}(1)


ãäå $P$, $V$ è $T$ – äàâëåíèå, îáúåì è
òåìïåðàòóðà ãàçà; $m$ – åãî ìàññà, $mu$ – ìàññà
ìîëÿ àçîòà, ðàâíàÿ $28cdot 10^{-3},{êã/ìîëü}$; $R$ – óíèâåðñàëüíàÿ
ãàçîâàÿ ïîñòîÿííàÿ.

Äëÿ îòâåòà íà âîïðîñ çàäà÷è íóæíî îïðåäåëèòü äàâëåíèå ãàçîîáðàçíîãî
àçîòà è ñðàâíèòü åãî ñ
ìàêñèìàëüíî äîïóñòèìûì.

Âûðàçèì èñêîìîå äàâëåíèå èç óðàâíåíèÿ 1:

begin{displaymath} P_x = {mRTovermu V},, end{displaymath}(2)


çäåñü íåèçâåñòíà ìàññà ãàçà, åå ìîæíî îïðåäåëèòü ÷åðåç îáúåì è
ïëîòíîñòü æèäêîãî àçîòà:
$m= rho_1V_1$. Âûðàæåíèå äëÿ èñêîìîãî äàâëåíèÿ â îáùåì âèäå:

begin{displaymath} P_x = {rho_1V_1RTovermu V},. end{displaymath}(3)


Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû èñêîìîé âåëè÷èíû:

begin{displaymath}[P_x]={{êã}cdot{ì}^3cdot{Äæ}cdot{Ê}cdot{ìîëü}over {ì}^3 ... ...{{Äæ}over{ì}^3}= {{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà.}end{displaymath}

Ýòî åäèíèöà äàâëåíèÿ â ÑÈ, ñëåäîâàòåëüíî, âûðàæåíèå â îáùåì âèäå
ïîëó÷åíî ïðàâèëüíî.

Âû÷èñëåíèÿ: ïîäñòàâèì ÷èñëà (âñå îíè äîëæíû áûòü âûðàæåíû â
ÑÈ):

begin{displaymath}P_x={8,1cdot 10^2cdot 5cdot 10^{-4}cdot 8,3 cdot 293over 28cdot 10^{-3}cdot 10^{-2}},{Ïà},.end{displaymath}

Ïðåæäå ÷åì âû÷èñëÿòü, ïðîâåäåì äåéñòâèÿ ñî ñòåïåíÿìè:

begin{displaymath}P_x={8,1cdot 5cdot 8,3 cdot 293over 28}cdot 10^{3},{Ïà}=3,52cdot 10^{6},{Ïà},.end{displaymath}

Èñêîìîå äàâëåíèå ðàâíî $3,52cdot 10^6,{Ïà}$ èëè $35,2 {àòì}$ è ïðåâûøàåò
äîïóñòèìîå.

Îòâåò: èñïàðåíèå æèäêîãî àçîòà äàííîé ìàññû â çàêðûòîì ñîñóäå
óêàçàííîãî îáúåìà íåëüçÿ
äîïóñòèòü, òàê êàê ïðè $20^circ C$ äàâëåíèå ïðåâûñèò
äîïóñòèìîå. Ïîýòîìó ñæèæåííûå ãàçû õðàíÿò
â îòêðûòûõ ñîñóäàõ.

Ïðèìåð 1.2. Öèëèíäðè÷åñêàÿ òðóáêà äëèíîé $ell$ íàïîëîâèíó ïîãðóæåíà â ðòóòü. Çàêðûâ åå ñâåðõó,
òðóáêó âûíèìàþò, ïðè ýòîì ÷àñòü ðòóòè âûëèâàåòñÿ. Êàêîé äëèíû ñòîëáèê
ðòóòè îñòàíåòñÿ â òðóáêå,
åñëè àòìîñôåðíîå äàâëåíèå ðàâíî $H$ ìì ðò. ñò.?

hbox to 0.4hsizeÐåøåíèå.
Ïðèìåì âîçäóõ, íàõîäÿùèéñÿ â òðóáêå íàä ðòóòüþ, çà èäåàëüíûé ãàç.
Ïîñêîëüêó â óñëîâèè çàäà÷è
èçìåíåíèå òåìïåðàòóðû íå îãîâîðåíî, ê ñòîëáèêó âîçäóõà ìîæíî ïðèìåíèòü
çàêîí Áîéëÿ – Ìàðèîòòà:

begin{displaymath} P_1V_1 = P_2V_2,, end{displaymath}(4)


ãäå $P_1$ è $V_1$ — äàâëåíèå è îáúåì
âîçäóõà â ïåðâîì ñîñòîÿíèè; $P_2$ è $V_2$ — òî æå âî
âòîðîì ñîñòîÿíèè.

begin{center}vbox{defbasepath{D:/html/work/link1/metod} defmetdir{met8} getpic{M21}}end{center}

Äëÿ îòâåòà íà âîïðîñ çàäà÷è íóæíî âûðàçèòü ïàðàìåòðû ãàçà ÷åðåç
èçâåñòíûå â îáùåì âèäå
âåëè÷èíû – $H$ è $ell$. Îáîçíà÷èì èñêîìóþ
äëèíó ñòîëáèêà ðòóòè ÷åðåç $X$.  ïåðâîì
ñîñòîÿíèè ñòîëáèê âîçäóõà äëèíîé $ell/2$, òî åñòü îáúåìîì
$V_1={Sellover 2}$ ($S$ – ïëîùàäü
ñå÷åíèÿ òðóáêè), íàõîäèëñÿ ïîä àòìîñôåðíûì äàâëåíèåì, òàê êàê òðóáêà
áûëà îòêðûòà ñâåðõó.
Âûðàçèì àòìîñôåðíîå äàâëåíèå: $P_1 = rho gH$,
ãäå $rho$ – ïëîòíîñòü ðòóòè. Òàêèì îáðàçîì,

begin{displaymath} P_1V_1 = rho gH{Sellover 2},. end{displaymath}(5)


Âî âòîðîì ñîñòîÿíèè äëèíà ñòîëáèêà âîçäóõà ñòàëà ðàâíîé $(ell-X)$, à åãî îáúåì $V_2=S(ell-X)$.
Äàâëåíèå âîçäóõà â ñóììå ñ äàâëåíèåì îñòàâøåãîñÿ ñòîëáèêà ðòóòè âûñîòîé
$X$ óðàâíîâåøèâàåòñÿ
àòìîñôåðíûì äàâëåíèåì, äåéñòâóþùèì ñîãëàñíî çàêîíó Ïàñêàëÿ íà íèæíèé
îòêðûòûé êîíåö òðóáêè:
$P_2+rho gX=rho gH$, îòêóäà äàâëåíèå

begin{displaymath}P_2=rho g(H-X) {è}end{displaymath}

begin{displaymath} P_2V_2 = rho g(H-X)S(ell-X),. end{displaymath}(6)


Ïîäñòàâèâ âûðàæåíèÿ (5 è 6)
â èñõîäíîå óðàâíåíèå (4) è
ñîêðàòèâ íà $g, S, rho$, ïîëó÷èì êâàäðàòíîå óðàâíåíèå
îòíîñèòåëüíî $X$:

begin{displaymath} X^2 - (H+ell)X+{ell Hover 2}=0,. end{displaymath}(7)


Äâà êîðíÿ ýòîãî óðàâíåíèÿ:

begin{displaymath}X_{1,2} = {(H+ell)pm sqrt{(H+ell)^2-2ell H}over 2}={(H+ell)pm sqrt{H^2+ell^2}over 2},.end{displaymath}

Ìàòåìàòè÷åñêàÿ ÷àñòü çàäà÷è âûïîëíåíà: íàéäåíû êîðíè êâàäðàòíîãî
óðàâíåíèÿ. Îäíàêî
óñëîâèþ ôèçè÷åñêîé çàäà÷è êîðåíü óðàâíåíèÿ ñî çíàêîì “+” íå
óäîâëåòâîðÿåò, òàê êàê äëèíà
ñòîëáèêà ðòóòè â ýòîì ñëó÷àå ïðåâûøàåò äëèíó òðóáêè $ell$. Ïîýòîìó

$X={(H+ell)-sqrt{H^2+ell^2}over 2}$. Âèäíî, ÷òî $X$ ïîëó÷èòñÿ â åäèíèöàõ äëèíû.
 ÷èñëîâîì âàðèàíòå ðåøåíèÿ ïîäîáíîé çàäà÷è $H$ è $ell$ íóæíî ïîäñòàâëÿòü â îäèíàêîâûõ
åäèíèöàõ äëèíû, íàïðèìåð, â ì.

Îòâåò: èñêîìàÿ äëèíà ñòîëáèêà âûðàæàåòñÿ òàê:

begin{displaymath}X={(H+ell)-sqrt{H^2+ell^2}over 2},.end{displaymath}


Ïðèìåð 1.3. Â ñòåêëÿííîì ñôåðè÷åñêîì ñîñóäå ñ
âíóòðåííèì äèàìåòðîì $3,{ñì}$ íàõîäèòñÿ àçîò,
äàâëåíèå êîòîðîãî ïðè òåìïåðàòóðå $-190^circ C$
ðàâíî 1,33 Ïà. Íà ñòåíêàõ âíóòðè ñîñóäà èìååòñÿ
ìîíîìîëåêóëÿðíûé (òîëùèíîé â îäíó ìîëåêóëó) ñëîé àäñîðáèðîâàííîãî, òî
åñòü ïîãëîùåííîãî
ïîâåðõíîñòíûì ñëîåì, àçîòà. Îäíà ìîëåêóëà çàíèìàåò ïëîùàäü
$10^{-15},{ñì}^2$. Íàéòè
äàâëåíèå àçîòà â ñîñóäå ïðè òåìïåðàòóðå $427^circ C$,
ïðè êîòîðîé îí ïîëíîñòüþ äåñîðáèðóåòñÿ
ñî ñòåíîê.

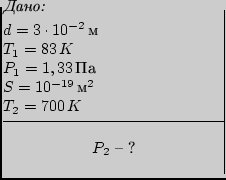hbox to 0.4hsizeÐåøåíèå.
Àçîò ïðè òàêîì íèçêîì äàâëåíèè ìîæíî ðàññìàòðèâàòü êàê èäåàëüíûé ãàç è
ïðèìåíèòü ñîîòâåòñòâóþùóþ òåîðèþ.
Èñêîìîå äàâëåíèå $P_2$ áóäåò ñêëàäûâàòüñÿ èç äàâëåíèÿ
ãàçà, ïåðâîíà÷àëüíî íàõîäèâøåãîñÿ
â ñîñóäå $P_2'$, è äàâëåíèÿ $P_2''$, êîòîðîå ñîçäàäóò
ìîëåêóëû, ïåðåøåäøèå ñî ñòåíîê
â cocóä ïðè òåìïåðàòóðå $T_2$:

begin{displaymath} P_2 = P_2'+P_2'',. end{displaymath}(8)


Âûðàçèì äàâëåíèå $P_2'$, ó÷èòûâàÿ, ÷òî ïîâûøåíèå
òåìïåðàòóðû ïðîèñõîäèò ïðè ïîñòîÿííîì
îáúåìå. Ñîãëàñíî çàêîíó Øàðëÿ:

begin{displaymath}{P_1over T_1}={P_2'over T_2},,end{displaymath}


begin{displaymath} {îòêóäàquadquad} P_2' = P_1{T_2over T_1},. end{displaymath}(9)


Âèäíî, ÷òî åäèíèöà èçìåðåíèÿ $P_2'$ ïîëó÷àåòñÿ òàêàÿ æå,
êàê $P_1$ – Ïà.

Äàâëåíèå $P_2''$ âûðàçèì èç îñíîâíîãî óðàâíåíèÿ
êèíåòè÷åñêîé òåîðèè èäåàëüíîãî ãàçà:

begin{displaymath} P_2'' = nkT_2={Nover V}kT_2,, end{displaymath}(10)


ãäå $N$ – îáùåå ÷èñëî äåñîðáèðîâàííûõ ìîëåêóë, $n$ – èõ êîíöåíòðàöèÿ,
$k$ – ïîñòîÿííàÿ Áîëüöìàíà, $V$ – îáúåì ñîñóäà:
$V={pi d^3over 6}$.
Îáùåå ÷èñëî ìîëåêóë, ïåðåøåäøèõ ñî ñòåíîê â ñîñóä, ìîæíî âûðàçèòü êàê
îòíîøåíèå
ïëîùàäè âíóòðåííåé ïîâåðõíîñòè ñôåðè÷åñêîãî ñîñóäà $pi d^2$
ê ïëîùàäè îäíîé ìîëåêóëû: $N={pi d^2over S}$. Îêîí÷àòåëüíî äëÿ äàâëåíèÿ $P_2''$ ïîëó÷èì:

begin{displaymath} P_2'' = {pi d^2cdot 6cdot kT_2over Spi d^3}={6kT_2over Sd},. end{displaymath}(11)


Ïðîâåðêà åäèíèö èçìåðåíèÿ èñêîìîé âåëè÷èíû:

begin{displaymath}[P_2'']={{Äæ}cdot{Ê}over{Ê}cdot{ì}^2cdot{ì}}= {{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà},.end{displaymath}

Ïîëó÷åíà åäèíèöà äàâëåíèÿ, òî åñòü âûðàæåíèå â îáùåì âèäå ïðàâèëüíî.

Òàêèì îáðàçîì,

begin{displaymath} P_2 = P_1 {T_2over T_1}+{6kT_2over Sd},. end{displaymath}(12)


Âû÷èñëåíèÿ:

begin{displaymath}P_2=left ({1,3cdot 7cdot 10^2over 83}+{6cdot 1,38cdot 1... ...7cdot 10^{2}over 10^{-19}cdot 3cdot 10^{-2}}right ),{Ïà}=end{displaymath}

begin{displaymath}=left ( 11,22+{6cdot 1,38 cdot 7over 3}right),{Ïà}=(11,22+19,32),{Ïà}=30,54,{Ïà},.end{displaymath}

Âèäíî, ÷òî ïî ïîðÿäêó âåëè÷èíû äåéñòâèå îáîèõ ôàêòîðîâ: ðîñòà äàâëåíèÿ
ñ ïîâûøåíèåì
òåìïåðàòóðû è óâåëè÷åíèÿ êîíöåíòðàöèè ìîëåêóë â ñîñóäå — ñîãëàñóåòñÿ
ïî ïîðÿäêó âåëè÷èí.
Âòîðîé ôàêòîð â äàííîì ñëó÷àå îêàçûâàåò áîëüøåå äåéñòâèå.

Читайте также:  Разрыв сосудов на ногах фото

Îòâåò: äàâëåíèå àçîòà â ñîñóäå ñòàíåò ðàâíûì 30,54 Ïà.

Ïðèìåð 1.4. Íàéòè ñðåäíåå ÷èñëî âñåõ ïàðíûõ
ñòîëêíîâåíèé â ñåêóíäó ìîëåêóë êèñëîðîäà,
íàõîäÿùèõñÿ â îáúåìå $1,{ñì}^3$ ïðè òåìïåðàòóðå $17^circ C$ è äàâëåíèè 666,5
Ïà.

hbox to 0.4hsizeÐåøåíèå.
Ñîãëàñíî ÌÊÒ èäåàëüíîãî ãàçà ñðåäíåå ÷èñëî ñòîëêíîâåíèé â ñåêóíäó

îäíîé
ìîëåêóëû

ðàâíî:

begin{displaymath} overline{Z} = sqrt{2}pi d^2noverline{v},, end{displaymath}(13)


ãäå $d$ – ýôôåêòèâíûé äèàìåòð ìîëåêóëû, $n$ – êîíöåíòðàöèÿ ãàçà, $overline{v}$
–
ñðåäíÿÿ àðèôìåòè÷åñêàÿ ñêîðîñòü ìîëåêóë.

Åñëè ó÷èòûâàòü òîëüêî ïàðíûå

ñòîëêíîâåíèÿ, ÷èñëî âñåõ ñòîëêíîâåíèé â
ñåêóíäó áóäåò áîëüøå â ${Nover 2}={nVover 2}$ ðàç, ãäå $N$ – îáùåå
÷èñëî ìîëåêóë.

Òîãäà èñêîìîå ÷èñëî ñòîëêíîâåíèé âûðàçèòñÿ òàê:

begin{displaymath} overline{Z}={sqrt{2}pi d^2overline{v}n^2Vover 2},. end{displaymath}(14)


Äàëåå ñëåäóåò âûðàçèòü êîíöåíòðàöèþ ãàçà èç îñíîâíîãî óðàâíåíèÿ
êèíåòè÷åñêîé òåîðèè
èäåàëüíîãî ãàçà: $p=nkT$, à ñðåäíþþ àðèôìåòè÷åñêóþ ñêîðîñòü
— ÷åðåç ïàðàìåòðû ãàçà:
$overline{v}=sqrt{8RToverpimu}$, ãäå $R$ — óíèâåðñàëüíàÿ (ìîëÿðíàÿ) ãàçîâàÿ ïîñòîÿííàÿ.
Ïîñëå ïîäñòàíîâêè äëÿ èñêîìîé âåëè÷èíû ïîëó÷àåòñÿ:

begin{displaymath} overline{Z}=2left({dPover kT}right)^2Vsqrt{pi RTovermu},. end{displaymath}(15)


 ýòîì âûðàæåíèè âñå, êðîìå äèàìåòðà ìîëåêóëû, èçâåñòíî. Ýòî ÷èñëî
âçÿòî èç òàáëèöû.

Ïðîâåðêà åäèíèöû èçìåðåíèÿ èñêîìîé âåëè÷èíû:

begin{displaymath}[overline{Z}]={{ì}^2cdot{Í}^2cdot{Ê}^2cdot{ì}^3cdot{Äæ}^... ... 2}over{ñ}cdot{ì}^{3over 2}cdot{êã}^{1over 2}}={ñ}^{-1},.end{displaymath}

Íàèìåíîâàíèå $c^{-1}$ ñîîòâåòñòâóåò ÷èñëó ñòîëêíîâåíèé â
ñåêóíäó.

Âû÷èñëåíèÿ:

begin{displaymath}overline{Z}={2cdot 12,25cdot 10^{-20}cdot (666,5)^2cdot ... ...over327cdot 10^{-3}},{ñ}^{-1} =3,3cdot 10^{24},{ñ}^{-1},.end{displaymath}

Îòâåò: ïðè óêàçàííûõ óñëîâèÿõ ïðîèñõîäèò
$3,3cdot 10^{24}$ ïàðíûõ ñòîëêíîâåíèé ìîëåêóë
â ñåêóíäó. Ýòî ÷èñëî çàâèñèò îò ïàðàìåòðîâ ñîñòîÿíèÿ ($P, T$), îáúåìà ãàçà è åãî
èíäèâèäóàëüíûõ õàðàêòåðèñòèê: äèàìåòðà ìîëåêóëû è ìîëÿðíîé ìàññû.

Ïðèìåð 1.5. Ðàññòîÿíèå ìåæäó ñòåíêàìè ñîñóäà ðàâíî $8,{ìì}$. Ïðè êàêîì äàâëåíèè âÿçêîñòü
ãàçà, íàõîäÿùåãîñÿ ìåæäó íèìè, íà÷íåò óìåíüøàòüñÿ ïðè îòêà÷êå?
Òåìïåðàòóðà ãàçà ðàâíà
$17^circ C$. Äèàìåòð ìîëåêóëû ñîñòàâëÿåò
$3cdot 10^{-10},{ì}$.

hbox to 0.4hsizeÐåøåíèå.
Òåîðåòè÷åñêè âÿçêîñòü ãàçà ïðè íå ñëèøêîì íèçêèõ äàâëåíèÿõ 
íå çàâèñèò îò íåãî:

begin{displaymath} eta = {1over 3}overline{v}overline{lambda}rho,, end{displaymath}(16)


òàê êàê $overline{lambda}$ – ñðåäíÿÿ äëèíà ñâîáîäíîãî ïðîáåãà ìîëåêóë îáðàòíî
ïðîïîðöèîíàëüíà äàâëåíèþ ïðè ïîñòîÿííîé òåìïåðàòóðå:

begin{displaymath} overline{lambda} = {1over sqrt{2}pi d^2n}={kTover sqrt{2}pi d^2P},, end{displaymath}(17)


à ïëîòíîñòü ãàçà $rho$ ïðÿìî ïðîïîðöèîíàëüíà äàâëåíèþ.
Âûðàæåíèå äëÿ ïëîòíîñòè èäåàëüíîãî ãàçà
ìîæíî ïîëó÷èòü èç óðàâíåíèÿ Êëàïåéðîíà – Ìåíäåëååâà:
$PV = {movermu}RT$, ó÷èòûâàÿ,
÷òî ïëîòíîñòü — ýòî ìàññà åäèíèöû îáúåìà:
$rho = {mover V}$. Ïîëó÷àåòñÿ, ÷òî
$rho = {mu Pover RT}$.

Ïðè íèçêîì äàâëåíèè ñðåäíÿÿ äëèíà ñâîáîäíîãî ïðîáåãà
ïåðåñòàåò
çàâèñåòü îò äàâëåíèÿ è îïðåäåëÿåòñÿ ðàçìåðàìè ñîñóäà:

begin{displaymath} overline{lambda} = ell,. end{displaymath}(18)


Ìîëåêóëû äâèæóòñÿ îò ñòåíêè ê ñòåíêå, íå ñòàëêèâàÿñü ìåæäó ñîáîé.
Âÿçêîñòü ãàçà íà÷íåò
óìåíüøàòüñÿ ïðè äàëüíåéøåé îòêà÷êå ñîñóäà çà ñ÷åò óìåíüøåíèÿ
êîíöåíòðàöèè ìîëåêóë
(ïëîòíîñòè ãàçà).

Äëÿ ðåøåíèÿ çàäà÷è íóæíî ïðèðàâíÿòü âûðàæåíèå äëÿ ñðåäíåé äëèíû
ñâîáîäíîãî
ïðîáeãa ìîëåêóë $overline{lambda}$ ðàññòîÿíèþ ìåæäó ñòåíêàìè ñîñóäà:

begin{displaymath}ell = {kTover sqrt{2}pi d^2P},end{displaymath}



è âûðàçèòü äàâëåíèå. Ïîëó÷àåì:

begin{displaymath} P = {kTover sqrt{2}pi d^2ell},. end{displaymath}(19)


 ýòîì âûðàæåíèè äëÿ äàâëåíèÿ âñå èçâåñòíî.

Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû èçìåðåíèÿ:

begin{displaymath}[P]={{Äæ}cdot{Ê}over{Ê}cdot{ì}^2cdot{ì}}={{Äæ}over {ì}^3}={{Í}cdot{ì}over{ì}^3}={{Í}over{ì}^2}={Ïà},.end{displaymath}

Âûðàæåíèå äëÿ äàâëåíèÿ â îáùåì âèäå ïîëó÷åíî ïðàâèëüíî.

Âû÷èñëåíèÿ:

begin{displaymath}P={1,38cdot 10^{-23}cdot 290over sqrt{2}cdot 3,14cdot 9... ...290over sqrt{2}cdot 3,14cdot 9cdot 8},{Ïà}=1,26, {Ïà},.end{displaymath}

Ïîëó÷åííîå ÷èñëî çíà÷èòåëüíî ìåíüøå âåëè÷èíû àòìîñôåðíîãî äàâëåíèÿ. Äëÿ
äàííîãî ãàçà ïðè íåèçìåííîé
òåìïåðàòóðå îíî îïðåäåëÿåòñÿ òîëüêî ðàçìåðàìè ñîñóäà $ell$.

Îòâåò: ïðè äàâëåíèè 1,26 Ïà âÿçêîñòü ãàçà íà÷íåò óìåíüøàòüñÿ
ïðè îòêà÷êå.
Óêàçàíèå: ïîäîáíûì îáðàçîì ðåøàþòñÿ çàäà÷è, ñâÿçàííûå ñ
êîýôôèöèåíòîì òåïëîïðîâîäíîñòè
èäåàëüíîãî ãàçà:

begin{displaymath}chi = {1over 3}overline{v}overline{lambda}rho c_v,,end{displaymath}



ãäå $c_v$ – óäåëüíàÿ òåïëîåìêîñòü
ïðè ïîñòîÿííîì îáúåìå:

begin{displaymath}c_v={iover 2}{Rovermu} (i{ -- ÷èñëî ñòåïåíåé ñâîáîäû ìîëåêóëû}).end{displaymath}


Ïðèìåð 1.6. 10 ë àçîòà, íàõîäÿùåãîñÿ ïîä äàâëåíèåì $10^5,{Ïà}$, ðàñøèðÿþòñÿ âäâîå.
Íàéòè êîíå÷íîå äàâëåíèå è ñîâåðøåííóþ ãàçîì ðàáîòó â ñëó÷àÿõ
èçîáàðè÷åñêîãî,
èçîòåðìè÷åñêîãî è àäèàáàòè÷åñêîãî ïðîöåññîâ. Ìîëåêóëû àçîòà èìåþò ïÿòü
ñòåïåíåé ñâîáîäû.

hbox to 0.4hsizeÐåøåíèå.
Ïðèìåì àçîò â äàííûõ óñëîâèÿõ çà èäåàëüíûé ãàç.
1. Ïðè èçîáàðè÷åñêîì ïðîöåññå äàâëåíèå ãàçà íå ìåíÿåòñÿ, ïîýòîìó $P_2=P_1$.
Ýëåìåíòàðíàÿ ðàáîòà ðàñøèðåíèÿ ðàâíà â îáùåì ñëó÷àå $PdV$, ãäå $P$ – äàâëåíèå,
$dV$ – áåñêîíå÷íî ìàëûé îáúåì. Ïîëíàÿ ðàáîòà íàõîäèòñÿ ïóòåì
èíòåãðèðîâàíèÿ, è âåëè÷èíà
eå çàâèñèò îò âèäà ïðîöåññà.

Ïðè èçîáàðè÷åñêîì ïðîöåññå

begin{displaymath} A_1=intlimits_{V_1}^{V_2}{PdV}=P(V_2-V_1),. end{displaymath}(20)


Ïðîâåðèì åäèíèöó èçìåðåíèÿ ðàáîòû:

begin{displaymath}[A]= {{Í}cdot {ì}^3over {ì}^2}={Í}cdot{ì}={Äæ},.end{displaymath}

2.  èçîòåðìè÷åñêîì ïðîöåññå òåìïåðàòóðà îñòàåòñÿ ïîñòîÿííîé, à
äàâëåíèÿ è îáúåìû â äâóõ
ñîñòîÿíèÿõ èäåàëüíîãî ãàçà ñâÿçàíû çàêîíîì Áîéëÿ – Ìàðèîòòà: $P_1V_1=P_2V_2$, îòêóäà
$P_2'={P_1V_1over V_2}$. Âèäíî, ÷òî çäåñü äëÿ åäèíèöû íåèçâåñòíîãî äàâëåíèÿ
ïîëó÷àåòñÿ
Ïà (ïàñêàëü).

Ðàáîòà èçîòåðìè÷åñêîãî ðàñøèðåíèÿ ðàññ÷èòûâàåòñÿ òàê:

begin{displaymath}A_2=int{PdV}=intlimits_{V_1}^{V_2}{{m over mu}RT{dVover V}}={movermu}RTln{V_2 over V_1},.end{displaymath}



Çäåñü äàâëåíèå âûðàæåíî èç óðàâíåíèÿ Êëàïåéðîíà – Ìåíäåëååâà.
Òåìïåðàòóðà
íåèçâåñòíà, ïîýòîìó, ïðèìåíèâ åùå ðàç óðàâíåíèå Êëàïåéðîíà –
Ìåíäåëååâà, ïîëó÷èì âûðàæåíèå
äëÿ èñêîìîé ðàáîòû ÷åðåç èçâåñòíûå â óñëîâèè âåëè÷èíû:

begin{displaymath} A_2 = P_1V_1ln{V_2over V_1},. end{displaymath}(21)


Ðåçóëüòàò íå èçìåíèòñÿ, åñëè ïîäñòàâèòü êîíå÷íûå äàâëåíèå è îáúåì $P_2$ è
$V_2$ èëè âìåñòî îòíîøåíèÿ ${V_2over V_1}$ âçÿòü ${P_1over P_2}$.

3. Êîíå÷íîå äàâëåíèå àäèàáàòè÷åñêîãî ðàñøèðåíèÿ âûðàçèì èç óðàâíåíèÿ
Ïóàññîíà:

begin{displaymath}P_2''=P_1left({V_1over V_2}right)^gamma,, {ãäå }gamma={C_pover C_V}={i+2over i}end{displaymath}



($i$ – ÷èñëî ñòåïåíåé ñâîáîäû ìîëåêóëû).

Ðàáîòà â ýòîì ïðîöåññå ñîâåðøàåòñÿ çà ñ÷åò óáûëè âíóòðåííåé ýíåðãèè
ãàçà:

begin{displaymath}A_3=-Delta u={movermu}C_V(T_1-T_2)={movermu}C_V T_1 left(1-{T_2over T_1}right),,end{displaymath}



ãäå $C_V$ – ìîëÿðíàÿ òåïëîåìêîñòü ïðè ïîñòîÿííîì îáúåìå:

begin{displaymath}C_V={iover 2}R={Rover gamma-1},.end{displaymath}

begin{center}vbox{getpic{M22}}end{center}

 ýòîé çàäà÷å òåìïåðàòóðû íå çàäàíû, ïîýòîìó îòíîøåíèå òåìïåðàòóð
ñëåäóåò çàìåíèòü îòíîøåíèåì
îáúåìîâ
${T_2over T_1}=left({V_1over V_2}right)^{gamma-1}$ è âîñïîëüçîâàòüñÿ
óðàâíåíèåì ñîñòîÿíèÿ èäåàëüíîãî ãàçà:

begin{displaymath}A_3={movermu}{Rover(gamma-1)}T_1left(1-{T_2over T_1}ri... ...amma-1)} left(1-left({V_1over V_2}right)^{gamma-1}right)=end{displaymath}


begin{displaymath} ={1overgamma-1}(P_1V_1-P_2''V_2),. end{displaymath}(22)


Çäåñü âñå èçâåñòíî, êîíå÷íîå äàâëåíèå ìîæíî ðàññ÷èòàòü îòäåëüíî.

Âû÷èñëåíèÿ:

  1. $P_2=P_1=10^{5},{Ïà},;quad A_1=10^{5}cdot 10^{-2},{Äæ}=10^{3},{Äæ}$.
  2. $P_2'={10^{5}cdot 10^{-2}over 2cdot 10^{-2}},{Ïà}=5cdot 10^{4},{Ïà},;$

    $A_2=10^{5}cdot 10^{-2}ln{2cdot 10^{-2}over 10^{-2}},{Äæ}=10^{3}ln{2},{Äæ}= 6,9cdot 10^2,{Äæ}.$

  3. $P_2''= 10^{5}cdot 0,5^{1,4},{Ïà}=3,8cdot 10^4,{Ïà},;$

    $A_3={1over 0,4}(10^3-760),{Äæ}=600,{Äæ},.$

Òàêèì îáðàçîì, íàèáîëüøåå èçìåíåíèå äàâëåíèÿ ïðîèñõîäèò ïðè
àäèàáàòè÷åñêîì ðàñøèðåíèè,
à íàèáîëüøàÿ ðàáîòà ñîâåðøàåòñÿ ïðè èçîáàðè÷åñêîì. Êà÷åñòâåííî
ðåçóëüòàòû ïðåäñòàâëåíû
íà ðèñóíêå. Ïëîùàäè ôèãóð ïîä ãðàôèêàìè ïðîöåññîâ ïîçâîëÿþò ñóäèòü î
ñîîòíîøåíèè ñîâåðøåííîé
ðàáîòû.

Îòâåò:
$10^{5},{Ïà},, 10^{3},{Äæ},; 5cdot 10^{4},{Ïà},, 690,{Äæ},; 3,8cdot 10^4,{Ïà},, 600,{Äæ}.$

Ïðèìåð 1.7. Õîëîäèëüíàÿ ìàøèíà, ðàáîòàþùàÿ ïî
îáðàòíîìó öèêëó Êàðíî, ïåðåäàåò òåïëîòó îò
õîëîäèëüíèêà ñ âîäîé ïðè òåìïåðàòóðå $0^circ C$
êèïÿòèëüíèêó ñ âîäîé ïðè òåìïåðàòóðå $100^circ$C.
Êàêóþ ìàññó âîäû íóæíî çàìîðîçèòü â õîëîäèëüíèêå, ÷òîáû ïðåâðàòèòü â
ïàð 1 êã âîäû â
êèïÿòèëüíèêå? Óäåëüíàÿ òåïëîòà ïàðîîáðàçîâàíèÿ âîäû ïðè $100^circ$Ñ ðàâíà
$2,26cdot 10^6,{Äæ/êã}$. Óäåëüíàÿ òåïëîòà ïëàâëåíèÿ ëüäà ðàâíà
$3,35cdot 10^5,{Äæ/êã}$.

Читайте также:  Семена льна для сосудов рецепт

hbox to 0.4hsizeÐåøåíèå.
Õîëîäèëüíàÿ ìàøèíà çà ñ÷åò âíåøíåé ðàáîòû îòíèìàåò íåêîòîðîå êîëè÷åñòâî
òåïëîòû $Q_2$
îò ìåíåå íàãðåòîãî òåëà ïðè òåìïåðàòóðå $T_2$ è
ïåðåäàåò òåïëîòó $Q_1$ áîëåå íàãðåòîìy òåëó
ïðè òåìïåðàòóðå $T_1$.
Êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ åå
$eta={Aover Q_1}={Q_1-Q_2over Q_1}$.

Òàêîå æå ñîîòíîøåíèå ñïðàâåäëèâî è äëÿ òåïëîâîé ìàøèíû, ñîâåðøàþùåé
ðàáîòó çà ñ÷åò ÷àñòè
òåïëîòû, âçÿòîé ó áîëåå íàãðåòîãî òåëà.

Íàèáîëüøèé êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ ñîîòâåòñòâóåò èäåàëüíîìó
(òåîðåòè÷åñêîìó) öèêëó Êàðíî.
 ýòîì ñëó÷àå
$eta={Q_1-Q_2over Q_1}={T_1-T_2over T_1}$, òî åñòü êïä
îïðåäåëÿåòñÿ òîëüêî
òåìïåðàòóðàìè íàãðåâàòåëÿ (òåëà ïðè òåìïåðàòóðå $T_1$) è
õîëîäèëüíèêà ($T_2$). Ñ ïîìîùüþ
ýòîãî ñîîòíîøåíèÿ ðåøàåòñÿ áîëüøèíñòâî çàäà÷, ñâÿçàííûõ ñ ðàáîòîé
òåïëîâûõ è õîëîäèëüíûõ ìàøèí.
 ðåàëüíûõ ìàøèíàõ êïä çíà÷èòåëüíî ìåíüøå, ÷åì
${T_1-T_2over T_1}$.

 äàííîé çàäà÷å êîëè÷åñòâî òåïëîòû $Q_1$, ïåðåäàâàåìîå áîëåå
íàãðåòîìó òåëó, ðàâíî $rm_1$,
à êîëè÷åñòâî òåïëîòû $Q_2$, âçÿòîå îò ìåíåå íàãðåòîãî òåëà,
ðàâíî $lambda m_2$, ïîýòîìó
ñïðàâåäëèâî ðàâåíñòâî:

begin{displaymath} {rm_1-lambda m_2over rm_1}={T_1-T_2over T_1},, end{displaymath}(23)


êîòîðîå ìîæíî ïðåîáðàçîâàòü òàê:

begin{displaymath}{lambda m_2over rm_1}={T_2over T_1},,end{displaymath}


begin{displaymath} {îòêóäà}quad m_2={rm_1T_2overlambda T_1},. end{displaymath}(24)


Ïðîâåðêà íàèìåíîâàíèÿ åäèíèöû:

begin{displaymath}[m]= {{Äæ}cdot {êã}cdot {Ê}cdot {êã}over{êã}cdot{Äæ}cdot {Ê}}={êã},.end{displaymath}

Âû÷èñëåíèÿ:

begin{displaymath}m_2={2,26cdot 10^{6}cdot 1cdot 273over 3,35cdot 10^{5}c... ...73},{êã}={2,26cdot 2730over 3,35cdot 373},{êã}=4,94,{êã}.end{displaymath}

Îòâåò: ÷òîáû èñïàðèòü 1 êã âîäû â êèïÿòèëüíèêå ïðè çàäàííûõ
óñëîâèÿõ, íóæíî
çàìîðîçèòü 4,94 êã âîäû â õîëîäèëüíèêå.

Äàëåå: 1.2. 
Çàäà÷è äëÿ ñàìîñòîÿòåëüíîãî
Ââåðõ: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è
Íàçàä: 1. 
Ìîëåêóëÿðíàÿ ôèçèêà è

ßÃÏÓ, Öåíòð èíôîðìàöèîííûõ
òåõíîëîãèé îáó÷åíèÿ

2005-09-21

Источник

https://vk-blog.com/texnologicheskaya-termodinamika-tt..

Часть задач есть решенные, https://vk.com/id5150215

1. Термодинамические параметры

1.1. Слиток свинца, имеющего плотность ρ = 11,3 г/см3, объемом V = 1 дм3 взвешен при помощи пружинных весов на полюсе, где ускорение свободного падения g90º = 9,8324 м/с2. Каков вес свинца, выраженный в ньютонах и в килограмм-силах? Что покажут пружинные весы на экваторе, где g0º = 9,780 м/с2?

1.2. Манометр, установленный в открытой кабине самолета, находящегося на земле, и измеряющий давление масла, показывает 6 кгс/см2 при показаниях барометра 752 мм рт.ст.

Каково абсолютное давление масла, выраженное в ньютонах на квадратный метр, килограмм илах на квадратный сантиметр, мегапаскалях, миллиметрах ртутного столба, миллиметрах водяного столба?
Каковы будут показания манометра в этих же единицах после подъема самолета на некоторую высоту, где атмосферное давление В = 442,5 мм рт.ст., если абсолютное давление остается неизменным?
Ускорение свободного падения [gм = 0,98055 м/с2] считать нормальным и не зависящим от высоты подъема самолета. Плотность ртути и воды принимать соответственно при 0º и 4ºС:

ρНg0ºС = 13,596 · 103 кг/м3; ρНg4ºС = 1,0 · 103 кг/м3.

1.3. В конденсаторе паровой турбины поддерживается абсолютное давление р = 0,004 МПа. Каковы показания вакуумметров, проградуированных в килоньютонах на квадратный метр, миллиметрах ртутного столба и в английских фунтах на квадратный дюйм, если в одном случае показания барометра составляют 735 мм рт.ст., а в другом – 764 мм рт.ст.?

1.4. Цилиндр диаметром d = 200 мм [рис. П.1.1]* плотно закрыт подвешенным на пружине поршнем, условно невесомым и скользящим без трения. В цилиндре образован вакуум, составляющий ω = 90% барометрического давления В = 0,101 МПа. Определить силу F натяжения пружины, если поршень неподвижен.

1.5. Для измерения малых избыточных давлений или небольших разряжений применяются микроманометры. Принципиальная схема прибора представлена на рис. П.1.2. Определить абсолютное давление в воздухопроводе 1, если длина столба l жидкости в трубке микроманометра 2, наклоненной под углом α = 30º, равна 180 мм. Рабочая жидкость – спирт плотностью ρ = 0,8 г/см3. Показание барометра 0,1020 МПа. Давление выразить в мегапаскалях, миллиметрах ртутного столба и в килограмм-силах на квадратный сантиметр.

1.3. В паросборнике находится водяной пар в количестве 300 кг. Определить объем паросборника, если удельный объем пара ν = 20,2 г/см3.

1.7. Объем баллона, содержащего газ под давлением р = 1,2 · 105 Па, составляет V = 6 л. Каким станет давление ρ2 газа в баллоне, если его соединить с другим баллоном объемом V* = 10 л, практически не содержащим газа [температура остается постоянной]?

1.8. В баллон емкостью V = 12 л поместили m1 = 1,5 кг азота при температуре t2 = 327ºС. Какое давление ρ2 будет создавать азот в баллоне при температуре t2 = 50ºС, если 35% азота будет выпущено? Каково будет начальное давление р1?

1.9. На дне сосуда, заполненного воздухом, лежит полный стальной шарик радиусом r = 2 см. Масса шарика mм = 5 г. До какого давления р надо сжать воздух в сосуде, чтобы шарик поднялся вверх? Считать, что воздух при больших давлениях подчиняется уравнению газового состояния. Температура воздуха t = 20ºС = const (сжатия воздуха происходит достаточно медленно).

1.10. При нагревании газа на 1 К при постоянном давлении его объем увеличился на 0,005 первоначального. При какой температуре находился газ?

1.11. Два баллона соединены трубкой с краном. В первом баллоне газ находится под давлением р1 = 2 · 105 Па, во втором – под давлением р2 = 1,2 · 105 Па. Емкость первого баллона V = 2 л, второго V = 6 л. Температура газов в обоих баллонах одинакова. Какое давление установится в баллонах, если открыть кран?

Читайте также:  Шейные позвонки и два сосуда

1.12. На какой глубине радиус пузырька воздуха вдвое меньше, чем у поверхности воды, если барометрическое давление у поверхности равно р2?

1.13. Цилиндр с газом разделен на четыре камеры тремя навесными поршнями (рис. П.1.3). В каждой секции находится газ, состояние которого характеризуется параметрами р1V1Т1, р2V2Т2, р3V3Т3. Каковы будут объемы и давления в каждой секции после того, как освободить поршни и дать им возможность свободно двигаться, а температуру изменить до Т2?

1.14. В U-образной трубке, запаянной с одного конца, высота столба воздуха l = 300 мм, а высота столба ртути h0 = 110 мм (рис. П.1.4). В правое колено долили столько ртути, что ее уровень поднялся на Δh0 = 40 мм. Насколько поднялся уровень ртути в левом колене? Атмосферное давление р0 = 1,01 · 105 Па (760 мм рт.ст.).

1.15. После погружения металлической трубки в резервуар с водой оказалось, что уровень воды в трубке поднялся на высоту 0,75 м при длине трубки 0,95 м. Определить глубину погружения трубки в резервуар Н, если барометрическое давление В = 750 мм рт.ст.

2. Законы идеальных газов. Уравнение состояния

2.1. Начальное состояние азота задано параметрами t = 200ºС, ν = 1,9 м3/кг. Азот нагревается при постоянном давлении, причем объем азота увеличивается до 5,7 м3/кг. Определить конечную температуру.

2.2. В цилиндре с подвижным поршнем находится кислород при t = 80ºС и разрежение (вакуум), равном 427 гПа. При постоянной температуре кислород сжимается до избыточного давления ризб = 1,2 МПа. Барометрическое давление В = 993 гПа. Во сколько раз уменьшится объем кислорода?

2.3. Баллон емкостью V, наполненный газом при давлении р и температуре Т взвесили, причем его вес оказался равным Р. Из баллона откачали часть газа, после чего давление упало до р1 при той же температуре. Вес баллона в этом случае оказался равным Р1. Определить плотность газа при нормальных условиях.

2.4. В комнате объемом V1 = 60 м3 температура поднялась с t1 = 17º до t2 = 27ºС. Давление при этом изменилось от р1 = 1,03 · 105 Па до р2 = 1,03 · 105 Па (среднюю массу одного киломоля воздуха принять равной μ = 29 кг/кмоль) На какую величину Δm изменилась масса воздуха в комнате?

2.5. Плотность пара некоторого соединения углерода с водородом равна ρ = 3 кг/м3 при температуре 43ºС и давлении 99 · 103 Па. Какова молекулярная масса этого соединения?

2.6. Определить температуру газа, находящегося в закрытом баллоне, если его давление, увеличилось на 0,4% первоначального при нагревании на ΔТ = 1 К.

2.7. Сколько ртути войдет в стеклянный баллончик объемом V0, нагретый до температуры t0, при его остывании до t1, если плотность ртути при t1 равна ρ (рис. П.1.5)?

2.8. Тонкостенный резиновый шар собственным весом Р = 0,6 Н наполнен неоном и погружен в озеро на глубину h = 120 м. Найти массу неона, если шар находится в положении равновесия. Атмосферное давление р0 = 1,03 · 105 Па температура в глубине озера t = + 4ºC. Натяжением резины пренебречь.

2.9. По газопроводной трубе идет углекислый газ при давлении р = 4,9 · 105 Па и температуре t = 21ºС. Какова скорость ν движения газа в трубе, если за время τ = 10 мин протекает m = 3 кг углекислого газа, а площадь сечения трубы S = 5 см2?

2.10. Стеклянная запаянная с одного конца трубка длиной l = 20 см, содержащая некоторое количество воздуха, погружена в ртуть так, что над поверхностью выступает l1 = 15 см трубки. Уровень ртути в трубке при 0ºС выше уровня ртути в сосуде на h1 = 5 см. На сколько градусов нужно было нагреть воздух в трубке, чтобы он мог занять весь объем трубки? Атмосферное давление р = 105 Па, уровень ртути в сосуде считать неизменным (рис. П.1.6).

2.11. Вертикально расположенный цилиндрический сосуд разделен на две равные части тяжелым теплонепроницаемым поршнем, который может скользить без трения. В верхней половине находится m1 граммов водорода при температуре Т1, нижней части – m2 граммов кислорода при температуре Т2. Сосуд перевернул. Чтобы поршень по-прежнему делил сосуд на две равные части, водород пришлось нагреть до температуры Т3. Температура кислорода осталась прежней. Определить, до какой температуры необходимо было нагреть водород и каково давление водорода в первом и втором случаях если вес поршня – Р, его сечение – S.

2.12. Абсолютное давление азота в сосуде при комнатной температуре (Г = 20º) р = 2,2 МПа. В сосуде азот нагревают, причем известно, что предельное избыточное дав?

Предыдущая статья
Бубновский упражнения для сердца и сосудов видео
Следующая статья
Идеальный газ находится в сосуде под поршнем ...
© Про сосуды от врачей отеля