Давление газа на стенки сосуда формула вывод
Îñíîâíîå óðàâíåíèå ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè óñòàíàâëèâàåò ñâÿçü ìåæäó äàâëåíèåì èäåàëüíîãî ãàçà è ñðåäíåé êèíåòè÷åñêîé ýíåðãèåé åãî ìîëåêóë.
Âûâîä îñíîâíîãî óðàâíåíèÿ ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè îñíîâûâàåòñÿ íà äîïóùåíèÿõ ìîäåëè èäåàëüíîãî ãàçà è óòâåðæäåíèè: äàâëåíèå ãàçà ÿâëÿåòñÿ ðåçóëüòàòîì óäàðîâ ìîëåêóë î ñòåíêó ñîñóäà.
Îïðåäåëèì äàâëåíèå ãàçà íà ñòåíêó ïëîùàäüþ S ñîñóäà ABCD.

Êàæäàÿ ìîëåêóëà ìàññîé m, îòñêàêèâàÿ îò ñòåíêè ïîñëå óïðóãîãî ñîóäàðåíèÿ ñî ñòåíêîé, ïåðåäàåò åé èìïóëüñ 2m0vx, ãäå vx— ïðîåêöèÿ ñêîðîñòè ìîëåêóëû 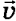 íà îñü Îõ, ïåðïåíäèêóëÿðíóþ ñòåíêå. Âñåãî çà îäíó ñåêóíäó ñóììàðíûé èìïóëüñ, ïîëó÷àåìûé ñòåíêîé îò âñåõ ìîëåêóë, ðàâåí 2m0vxZ, ãäå Z — ÷èñëî òàêèõ ñòîëêíîâåíèé (çà 1 ñ) âñåõ ìîëåêóë. Î÷åâèäíî, ÷òî
íà îñü Îõ, ïåðïåíäèêóëÿðíóþ ñòåíêå. Âñåãî çà îäíó ñåêóíäó ñóììàðíûé èìïóëüñ, ïîëó÷àåìûé ñòåíêîé îò âñåõ ìîëåêóë, ðàâåí 2m0vxZ, ãäå Z — ÷èñëî òàêèõ ñòîëêíîâåíèé (çà 1 ñ) âñåõ ìîëåêóë. Î÷åâèäíî, ÷òî 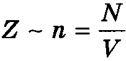 , ãäå n — êîíöåíòðàöèÿ ìîëåêóë â åäèíèöå îáúåìà; N — ÷èñëî âñåõ ìîëåêóë. ×èñëî Z ïðîïîðöèîíàëüíî òàêæå ñêîðîñòè ìîëåêóë vxè ïëîùàäè ñòåíêè S: Z~ nvxS. Ïîñêîëüêó âñå íàïðàâëåíèÿ ïðè õàîòè÷íîì äâèæåíèè ìîëåêóë ãàçà ðàâíîâåðîÿòíû, òî èç âñåõ ìîëåêóë, èìåþùèõ ñîñòàâëÿþùóþ ñêîðîñòè vx, òîëüêî ïîëîâèíà äâèæåòñÿ â ñòîðîíó ñòåíêè CD, âòîðàÿ ïîëîâèíà — â ñòîðîíó À (ò.å. â îáðàòíóþ). Ïîýòîìó
, ãäå n — êîíöåíòðàöèÿ ìîëåêóë â åäèíèöå îáúåìà; N — ÷èñëî âñåõ ìîëåêóë. ×èñëî Z ïðîïîðöèîíàëüíî òàêæå ñêîðîñòè ìîëåêóë vxè ïëîùàäè ñòåíêè S: Z~ nvxS. Ïîñêîëüêó âñå íàïðàâëåíèÿ ïðè õàîòè÷íîì äâèæåíèè ìîëåêóë ãàçà ðàâíîâåðîÿòíû, òî èç âñåõ ìîëåêóë, èìåþùèõ ñîñòàâëÿþùóþ ñêîðîñòè vx, òîëüêî ïîëîâèíà äâèæåòñÿ â ñòîðîíó ñòåíêè CD, âòîðàÿ ïîëîâèíà — â ñòîðîíó À (ò.å. â îáðàòíóþ). Ïîýòîìó 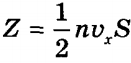 , à ïîëíûé èìïóëüñ, ïåðåäàííûé ñòåíêå çà 1 ñ, ðàâåí 2m0vxZ = m0nvx2S. Ïîñêîëüêó èçìåíåíèå èìïóëüñà òî÷êè (òåëà) çà åäèíèöó âðåìåíè ðàâíî äåéñòâóþùåé íà íåãî ñèëå
, à ïîëíûé èìïóëüñ, ïåðåäàííûé ñòåíêå çà 1 ñ, ðàâåí 2m0vxZ = m0nvx2S. Ïîñêîëüêó èçìåíåíèå èìïóëüñà òî÷êè (òåëà) çà åäèíèöó âðåìåíè ðàâíî äåéñòâóþùåé íà íåãî ñèëå 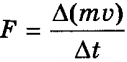 .  äåéñòâèòåëüíîñòè, ïîñêîëüêó ðå÷ü èäåò î áîëüøîì êîëè÷åñòâå ìîëåêóë, äâèæóùèõñÿ ñ ðàçíûìè ñêîðîñòÿìè, ñèëó ñëåäóåò óñðåäíèòü:
.  äåéñòâèòåëüíîñòè, ïîñêîëüêó ðå÷ü èäåò î áîëüøîì êîëè÷åñòâå ìîëåêóë, äâèæóùèõñÿ ñ ðàçíûìè ñêîðîñòÿìè, ñèëó ñëåäóåò óñðåäíèòü:  .
.
Ñèëà ýòà çàâèñèò, òàêèì îáðàçîì, îò ñðåäíåãî êâàäðàòà ñêîðîñòè  . Ïîñêîëüêó âñëåäñòâèå õàîòè÷íîñòè äâèæåíèÿ âñå íàïðàâëåíèÿ ðàâíîïðàâíû, òî:
. Ïîñêîëüêó âñëåäñòâèå õàîòè÷íîñòè äâèæåíèÿ âñå íàïðàâëåíèÿ ðàâíîïðàâíû, òî:

Ñ äðóãîé ñòîðîíû, èçâåñòíî, ÷òî êâàäðàò ìîäóëÿ ëþáîãî âåêòîðà ðàâåí ñóììå êâàäðàòîâ åãî ïðîåêöèé íà îñè êîîðäèíàò, ïîýòîìó:

Óñðåäíÿÿ ýòî âûðàæåíèå ïî âñåì ìîëåêóëàì è ó÷èòûâàÿ  , ïîëó÷èì:
, ïîëó÷èì:

Îòñþäà:
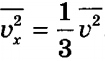
Ñ ó÷åòîì ïîñëåäíåé ôîðìóëû 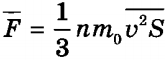 .
.
Ñëåäîâàòåëüíî, äàâëåíèå íà ñòåíêó ñîñóäà ðàâíî:

Ýòî îñíîâíîå óðàâíåíèå ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè. Ýòî óðàâíåíèå — ïåðâîå êîëè÷åñòâåííîå ñîîòíîøåíèå, ïîëó÷åííîå â ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè. Óðàâíåíèå  ïîçâîëÿåò ïîëó÷èòü ñâÿçü ìåæäó äàâëåíèåì è ñðåäíåé êèíåòè÷åñêîé ýíåðãèåé ìîëåêóë
ïîçâîëÿåò ïîëó÷èòü ñâÿçü ìåæäó äàâëåíèåì è ñðåäíåé êèíåòè÷åñêîé ýíåðãèåé ìîëåêóë  .
.
 .
.
Äàâëåíèå èäåàëüíîãî ãàçà ðàâíî äâóì òðåòÿì ñðåäíåé êèíåòè÷åñêîé ýíåðãèè ïîñòóïàòåëüíîãî äâèæåíèÿ ìîëåêóë, ñîäåðæàùèõñÿ â åäèíèöå îáúåìà.
Âàæíî ïîä÷åðêíóòü, ÷òî çäåñü ðå÷ü èäåò î ñðåäíåé êèíåòè÷åñêîé ýíåðãèè ìîëåêóë ãàçà. Ýòî îçíà÷àåò, ÷òî äàâëåíèå ãàçà — âåëè÷èíà, îðãàíè÷åñêè ñâÿçàííàÿ ñ òåì, ÷òî ãàç ñîñòîèò èç áîëüøîãî ÷èñëà ìîëåêóë. Íåò ñìûñëà ãîâîðèòü î äàâëåíèè, ñîçäàâàåìîì íåñêîëüêèìè ìîëåêóëàìè. Äàâëåíèå ãàçà – ïîíÿòèå, èìåþùåå ñòàòèñòè÷åñêèé õàðàêòåð (òàê íàçûâàþò ïîíÿòèÿ, èìåþùèå ñìûñë òîëüêî äëÿ ñèñòåì ñ î÷åíü áîëüøèì ÷èñëîì ÷àñòèö).
Êàëüêóëÿòîðû ïî ôèçèêå | |
| Ðåøåíèå çàäà÷ ïî ôèçèêå, ïîäãîòîâêà ê ÝÃÅ è ÃÈÀ, ìåõàíèêà òåðìîäèíàìèêà è äð. | |
| Êàëüêóëÿòîðû ïî ôèçèêå | |
Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ôèçèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ìîëåêóëÿðíîêèíåòè÷åñêàÿ òåîðèÿ ôîðìóëû | |
| Îñíîâû ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè, îñíîâíîå óðàâíåíèå ÌÊÒ èäåàëüíîãî ãàçà, ñðåäíåêâàäðàòè÷íàÿ ñêîðîñòü ìîëåêóë, ñðåäíÿÿ êèíåòè÷åñêàÿ ýíåðãèÿ ïîñòóïàòåëüíîãî äâèæåíèÿ ìîëåêóë è òä. | |
| Ìîëåêóëÿðíîêèíåòè÷åñêàÿ òåîðèÿ ôîðìóëû | |
Ìîëåêóëÿðíàÿ ôèçèêà | |
| Êèïåíèå, èñïàðåíèå, êîíäåíñàöèÿ, ïëàâëåíèå, êðèñòàëèçàöèÿ æèäêîñòè, âëàæíîñòü, àòîìíàÿ ìàññà, îñíîâû ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè | |
| Ìîëåêóëÿðíàÿ ôèçèêà | |
Источник
Макеты страниц
Стенки сосуда, в котором заключен газ, подвергаются непрерывной бомбардировке молекулами. В результате элементу стенки сообщается за секунду некоторый импульс, который равен силе, действующей на . Отношение этой силы к величине дает давление, оказываемое газом на стенки сосуда. Вследствие хаотичности движения молекул давление газа на различные участки стенок сосуда одинаково (разумеется, при условии, что газ находится в равновесном состоянии).
Если предположить, что молекулы отскакивают от стенки по закону зеркального отражения величина скорости молекулы не изменяется, то импульс, сообщаемый при ударе стенке молекулой, будет равен (рис. 96.1; — масса молекулы). Этот импульс направлен по нормали к площадке. Каждая из молекул (см. (95.2)) сообщает стенке импульс а все эти молекулы — импульс
Просуммируем полученное выражение по направлениям в пределах телесного угла (отвечающего изменениям Ф от 0 до и изменениям от 0 до .
Рис. 96.1.
В результате получим импульс, сообщаемый молекулами, скорости которых имеют величину от v до
(мы подставили выражение (94.4) для Интегрирование по дает интеграл по равен 1/3. Следовательно,
Проинтегрировав это выражение по скоростям от 0 до получим полный импульс, сообщаемый площадке за время
Выражение
представляет собой среднее значение квадрата скорости молекул. Заменив в (96.1) интеграл произведением получим, что
есть число молекул в единице объема). Наконец, разделив это выражение на и получим давление газа на стенки сосуда:
Масса всех молекул по предположению одинакова. Поэтому ее можно внести под знак среднего. В результате выражение (96.2) примет вид
где — среднее значение кинетической энергии поступательного движения молекул.
Получим выражение для давления, исходя из упрощенных представлений, которые привели нас к формуле (95.7). Согласно этим представлениям каждая молекула сообщает стенке при ударе импульс Умножив этот импульс на число ударов (см. (95.7)), получим импульс, сообщаемый единичной площадке в единицу времени, т. е. давление.
Таким образом, получается формула
Эта формула отличается от (96.2) тем, что вместо среднего квадрата скорости стоит квадрат средней скорости Впоследствии (см. § 97) мы убедимся в том, что эти две величины отличаются друг от друга, т. е.
При более аккуратном подсчете нужно число молекул, определяемое формулой (95.8), умножить на и затем произвести суммирование по всем V. В результате получится импульс, сообщаемый площадке за время
Разделив это выражение на и получим для давления формулу (96-2). Таким образом, исходя из упрощенного представления о движении молекул вдоль трех взаимно перпендикулярных направлений, мы получили точное выражение для давления. Это объясняется тем, что указанное упрощение приводит, с одной стороны, к занижению числа ударов молекул о стенку вместо см. (95.6) и (95.7)), а с другой — к завышению импульса, передаваемого стенке при каждом ударе. При упрощенном выводе мы принимали, что при каждом ударе стенке сообщается импульс, равный . В действительности же величина сообщаемого стенке импульса зависит от угла вследствие чего средний импульс, сообщаемый при одном ударе, равен . В итоге обе неточности взаимно компенсируют друг друга и, несмотря на упрощенность рассмотрения, получается точное выражение для давления.
Источник
Рассмотрим подробнее, что представляет собой один из основных параметров состояния – давление P. Ещё в XVIII веке Даниил Бернулли предположил, что давление газа есть следствие столкновения газовых молекул со стенками сосуда. Именно давление чаще всего является единственным сигналом присутствия газа.
Итак, находящиеся под давлением газ или жидкость действуют с некоторой силой на любую поверхность, ограничивающую их объем. В этом случае сила действует по нормали к ограничивающей объем поверхности. Давление на поверхность равно:
| , |
где ΔF – сила, действующая на поверхность площадью ΔS.
Можно также говорить о давлении внутри газа или жидкости. Его можно измерить, помещая в газ или жидкость небольшой куб с тонкими стенками, наполненный той же средой (рис. 1.1).

Рис. 1.1
Поскольку среда покоится, на каждую грань куба со стороны среды действует одна и та же сила ΔF. В окрестности куба давление равно ΔF/ΔS, где ΔS – площадь грани куба. Из этого следует, что внутреннее давление является одним и тем же во всех направлениях и во всем объеме независимо от формы сосуда. Этот результат называется законом Паскаля: если к некоторой части поверхности, ограничивающей газ или жидкость, приложено давление P0, то оно одинаково передается любой части этой поверхности.
Допустим, автомобиль поднимается гидравлическим домкратом, состоящим, как показано на рисунке 1.2, из двух соединенных трубкой цилиндров с поршнями. Диаметр большого цилиндра равен 1 м, а диаметр малого – 10 см. Автомобиль имеет вес F2. Найдем силу давления на поршень малого цилиндра, необходимую для подъема автомобиля.
Рис. 1.2
Поскольку оба поршня являются стенками одного и того же сосуда, то в соответствии с законом Паскаля они испытывают одинаковое давление. Пусть – давление на малый поршень, а – давление на большой поршень. Тогда, т.к. P1 = P2, имеем:
| , |
Отсюда F1=F2(S1/S2)=0,01F2
Таким образом, для подъема автомобиля достаточно давить на малый поршень с силой, составляющей лишь 1 % веса автомобиля.
Вычислим давление, оказываемое газом на одну из стенок сосуда (рис. 1.3).

Рис. 1.3
Обозначим: n – концентрация молекул в сосуде; m0 – масса одной молекулы. Движение молекул по всем осям равновероятно, поэтому к одной из стенок сосуда площадью S, подлетает в единицу времени (1/6)nvx молекул, где vx – проекция вектора скорости на направление, перпендикулярное стенке.
Каждая молекула обладает импульсом m0υx, но стенка получает импульс 2m0υx(при абсолютно-упругом ударе m0υx- (-m0υx)=2m0υx). За время dt о стенку площадью S успеет удариться число молекул, которое заключено в объёме V:
| , |
Общий импульс, который получит стенка S:
| , |
Разделив обе части равенства на S и dt, получим выражение для давления:
| , | (1.2.1) |
Таким образом, мы определили давление как силу, действующую в единицу времени на единицу площади:
| , | (1.2.2) |
Наивно полагать, что все молекулы подлетают к стенке S с одной и той же скоростью vx (рис. 1.3). На самом деле молекулы имеют разные скорости, направленные в разные стороны, то есть скорости газовых молекул – случайные величины.
Более точно случайную величину характеризует среднеквадратичная величина. Поэтому под скоростью vx2понимаем среднеквадратичную скорость <vx2> . Вектор скорости, направленный произвольно в пространстве, можно разделить на три составляющих:
| , |
Ни одной из этих проекций нельзя отдать предпочтение из-за хаотичного теплового движения молекул, то есть в среднем . Следовательно, на другие стенки будет точно такое же давление. Тогда можно записать в общем случае:
или
| (1.2.3) |
где <Ek>– средняя энергия одной молекулы. Это и есть основное уравнение молекулярно-кинетической теории газов.
Итак, давление газов определяется средней кинетической энергией поступательного движения молекул.
Уравнение (1.2.3) называют основным уравнением, потому что давление Р – макроскопический параметр системы здесь связан с основными характеристиками – массой и скоростью молекул.
Иногда за основное уравнение принимают выражение
Рассмотрим единицы измерения давления.
По определению, , поэтому размерность давления Н/м2.
1 Н/м2 = 1 Па; 1 атм. = 9,8 Н/см2 = 98066 Па ≈105 Па,
1 мм рт.ст. = 1 тор = 1/760 атм. = 133,3 Па,
1 бар = 105 Па; 1 атм. = 0,98 бар.
Источник
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
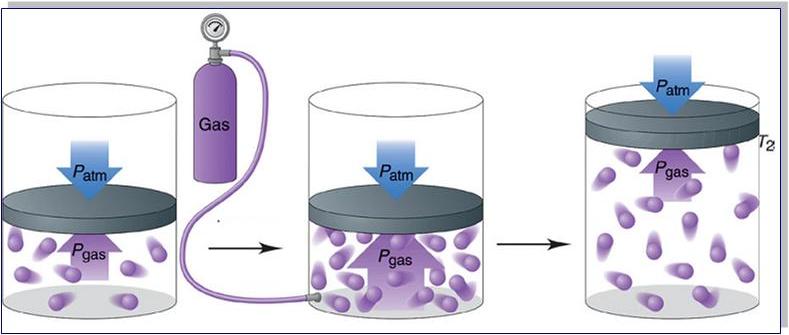
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
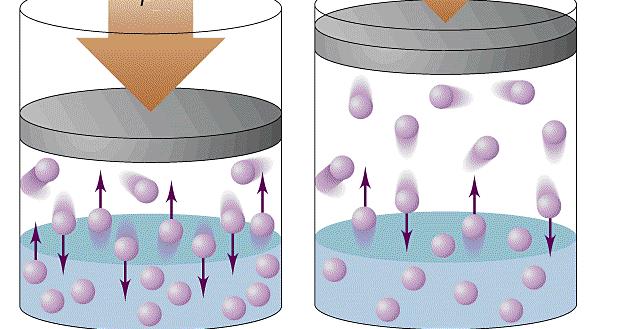
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
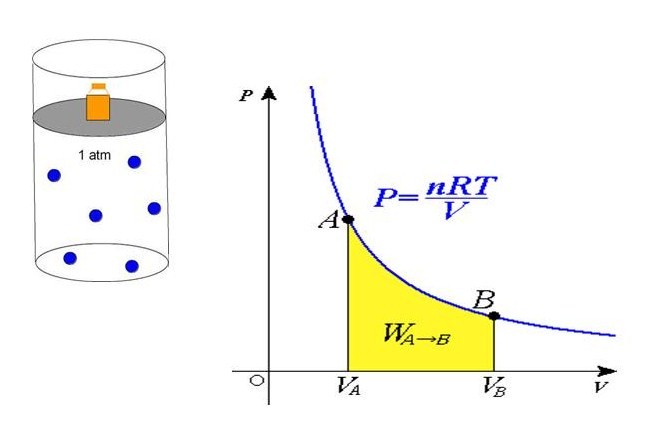
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
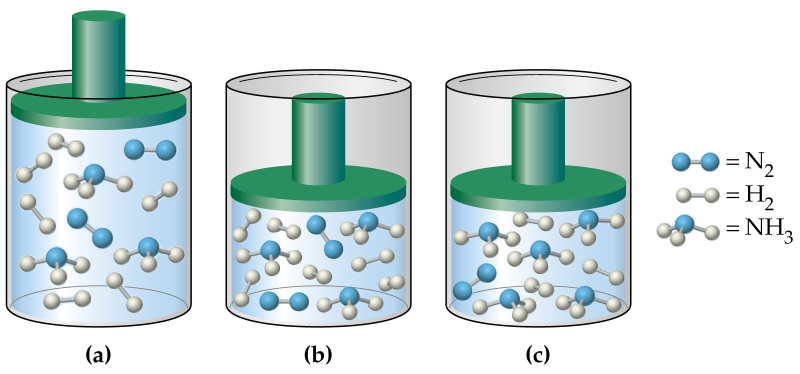
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
