Давление газа на стенки сосуда тем больше чем больше
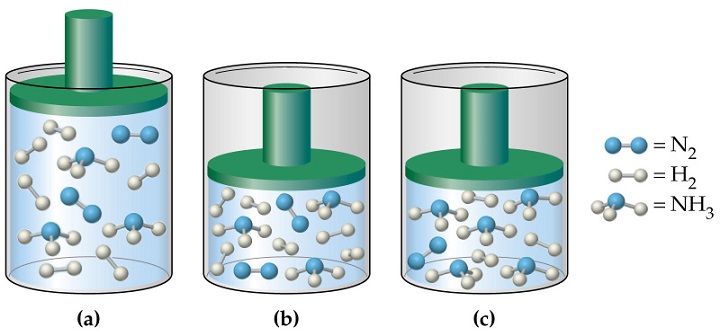
В жизни мы встречаем газообразное состояние вещества, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (он занимает весь предоставленный ему объем), состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.
Агрегатных состояния точно три?
На самом деле, есть еще четвертое – плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ – газ, в котором помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Давление газа
Мы только что выяснили, что молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.
Например, в комнате, в которой вы сейчас находитесь, на каждый квадратный сантиметр за 1 с молекулами воздуха наносится столько ударов, что их количество выражается двадцати трехзначным числом.
Хотя сила удара отдельной молекулы мала, действие всех молекул о стенки сосуда приводит к значительному давлению. Это как если бы один комар толкал машину, то она бы и не сдвинулась с места, а вот пару сотен миллионов комаров вполне себе способны эту машину сдвинуть.
Зависимость давления от других величин
Зависимость давления от объема
В механике есть формула давления, которая показывает: давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.
Давление
p = F/S
p – давление [Па]
F – сила [Н]
S – площадь [м^2]
То есть, если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы они толкали грузовой автомобиль (просто потому что легковая меньше грузовика).
Из формулы давления следует, что давление на легковой автомобиль будет больше из-за меньшей площади.
Давайте рассмотрим аналогичный пример с двумя сосудами разной площади.
Давление в левом сосуде будет больше, чем во втором, по аналогичной схеме – потому что площадь меньше. Но если площадь основания меньше, то и объем меньше. Это значит, что давление будет зависеть от объема следующим образом: чем больше объем, тем меньше давление – и наоборот.
При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):
Такая зависимость называется законом Бойля-Мариотта.
Она экспериментально проверяется с помощью такой установки.
Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.
Зависимость давления от температуры
Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Эти исследования были впервые произведены в Жаком Шарлем.
Газ нагревался в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Пренебрегая ничтожным увеличением объема колбы при нагревании и незначительным изменением объема при смещении ртути в узкой манометрической трубке.
Таким образом, можно считать объем газа неизменным. Подогревая воду в сосуде, окружающем колбу, измеряли температуру газа по термометру, а соответствующее давление – по манометру.
Этот эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.
С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейно:
Эта зависимость называется законом Шарля.
Хранение и транспортировка газов
Если нужно перевезти значительное количество газа из одного места в другое, или когда газы необходимо длительно хранить – их помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.
Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.
Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или любым способом пытаться сделать в них отверстие, даже после использования.
Понимать и любить этот мир проще, когда разбираешься в физике. В этом помогут небезразличные и компетентные преподаватели онлайн-школы Skysmart.
Чтобы формулы и задачки ожили и стали более дружелюбными, на уроках мы разбираем примеры из обычной жизни современных подростков. Приходите на бесплатный вводный урок по физике и начните учиться в удовольствие уже завтра!
Источник
Давление газа – что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ – это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.
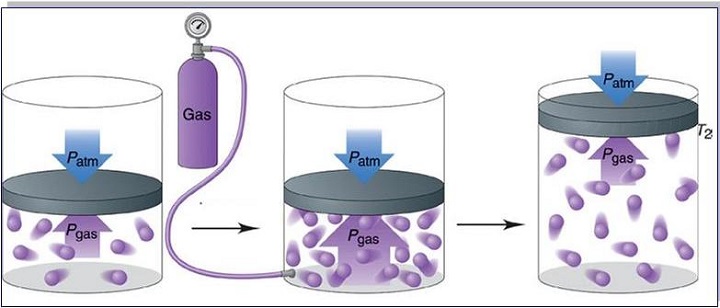
Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
(P=frac{F}{S})
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия – это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
(F*Δt = Δp)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.
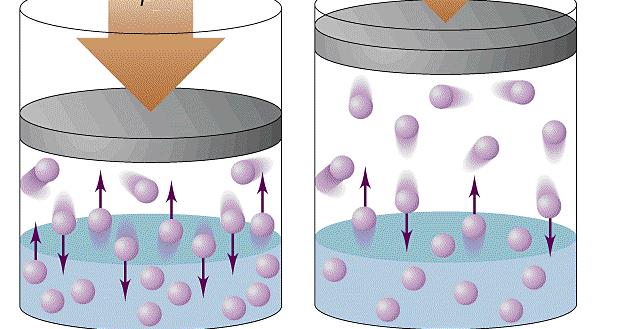
Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения. При этом можно наблюдать небольшой процент частиц со скоростями, приближенными к нулю, и малую долю частиц, обладающих огромной скоростью. Средняя квадратичная скорость в этом случае будет соответствовать некоторой величине, не изменяющейся с течением времени.
Средняя квадратичная скорость частиц однозначно характеризует температуру газа. Используя приближения молекулярно-кинетической теории в виде невзаимодействующих безразмерных и хаотично движущихся частиц, получают формулу для расчета давления газа в сосуде:
(P=frac{N*m*v^{2}}{3*V})
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
(P*V = n*R*T )
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
(P=frac{n*R*T}{V})
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.
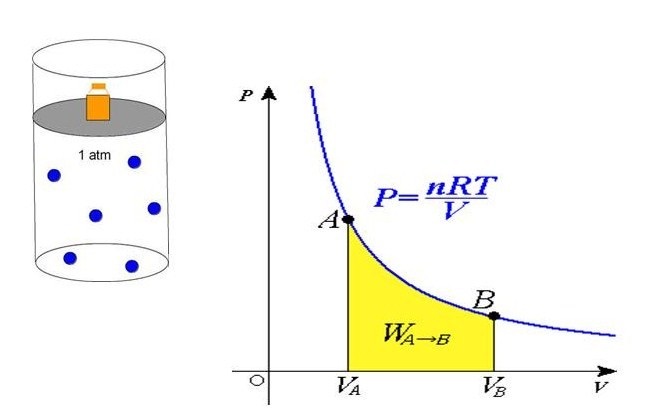
Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.

Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
- Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример
Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.
Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:
(P=frac{N*m*v^{2}}{3*V})
Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:
(m=frac{M}{NA})
(n=frac{N}{NA})
(m*N= M*n)
(P=frac{M*n*v^{2}}{3*V})
Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.
Источник
Мякишев Г.Я. Давление газа в сосуде //Квант. – 1987. – № 9. – С. 41-42.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Зависит ли давление газа на стенку сосуда от материала стенки и ее температуры? Попробуем ответить на этот вопрос.
При выводе основного уравнения молекулярно-кинетической теории идеального газа в учебнике «Физика 9» (§7) предполагается, что стенка абсолютно гладкая и столкновения молекул со стенкой происходят по закону абсолютно упругого удара. Другими словами, кинетическая энергия молекулы при ударе не меняется, и угол падения молекулы равен углу отражения. Является ли это предположение оправданным и необходимым?
Коротко можно сказать так: предположение оправдано, но не необходимо.
На первый взгляд кажется, что считать стенку абсолютно гладкой ни в коем случае нельзя – стенка сама состоит из молекул и, значит, гладкой быть не может. Из-за этого угол падения .не может при любом соударении равняться углу отражения. Кроме того, молекулы стенки совершают хаотические колебания около положений равновесия (участвуют в беспорядочном тепловом движении). Поэтому при столкновении с какой-либо молекулой стенки молекула газа может передать часть энергии стенке или, наоборот, увеличить свою кинетическую энергию за счет стенки.
Тем не менее предположение об абсолютно упругом характере соударения молекулы газа со стенкой оправдано. Дело в том, что при вычислении давления в конечном счете важны средние значения соответствующих величин. При условии теплового равновесия между газом и стенкой сосуда кинетическая энергия молекул газа в среднем остается неизменной, т. е. соударения со стенкой не меняют среднюю энергию молекул газа. Если бы это было не так, то тепловое равновесие самопроизвольно нарушалось бы. А это невозможно согласно второму закону термодинамики. Также не может быть преимущественного отражения молекул в каком-либо определенном направлении – иначе сосуд с газом начал бы двигаться, что противоречит закону сохранения импульса. Значит, среднее число молекул, падающих на стенку под некоторым углом, равно среднему числу молекул, отлетающих от стенки под таким же углом. Предположение о зеркальном отражении от стенки каждой отдельной молекулы соответствует этому условию.
Таким образом, считая соударения молекул газа со стенкой упругими, мы получаем для среднего давления такой же результат, как и без этого предположения. Значит, давление газа не зависит от качества обработки стенки (ее гладкости). Однако предположение об абсолютно упругом характере удара сильно упрощает вычисление давления газа, и поэтому оно оправдано.
А зависит ли давление газа на стенку от ее температуры? На первый взгляд – должно зависеть. Если, например, нет теплового равновесия, то молекулы от холодной стенки должны отскакивать с меньшей энергией, чем от горячей.
Однако, даже если одну стенку поддерживать холодной с помощью холодильной установки, то давление на нее все равно не может быть меньше, чем давление на противоположную горячую стенку. Ведь тогда сосуд начал бы двигаться ускоренно без внешних сил, а это противоречит законам механики: освободив закрепленный сосуд со стенками различной температуры, мы не вызовем его смещения. Дело здесь в том, что при данном неравновесном состоянии газа в сосуде концентрация молекул у холодной стенки больше, чем у горячей. Уменьшение кинетической энергии молекул у холодной стенки компенсируется увеличением концентрации молекул и наоборот. В результате давление на холодную и горячую стенки оказывается одним и тем же.
Рассмотрим еще один вариант опыта. Охладим очень быстро одну из стенок. В первый момент давление на нее уменьшится, и сосуд немного сдвинется с места; затем давления выравняются, и сосуд остановится[1]. Но при этом движении центр масс системы останется на месте из-за того, что плотность газа у холодной стенки станет чуть больше, чем у горячей.
Следует отметить, что на самом деле давление не остается строго фиксированной величиной. Оно испытывает флуктуации, и поэтому сосуд слегка «дрожит» на месте. Но амплитуда дрожания сосуда крайне мала.
Итак, окончательно мы пришли к выводу, что давление газа на стенки в сосуде не зависит ни от качества обработки стенок, ни от их температуры.
Примечания
- ↑ Остановка сосуда произойдет из-за того, что молекулы газа при ударе передают больший импульс той стенке, которая движется им навстречу.
Источник

1. Твёрдые тела оказывают давление на опору. На тело, стоящее на опоре, действуют сила тяжести ( vec{F}_т=mvec{g} ) и сила реакции опоры ( vec{N} ) (рис. 55).
Если опора неподвижна, то это тело действует на неё с силой ( vec{F} ), называемой силой давления и равной в этом случае по модулю силе тяжести: ( F=mg ).
Физическая величина, равная отношению силы давления ( F ) к площади поверхности ( S ) называется давлением и обозначается буквой ( p ):
[ p=F/S ]
Единицей давления является 1 паскаль (1 Па):
[ [,p,]=1Н/1м^2=1,Н/м^2=1,Па ]
Более крупная единица давления – килопаскаль.
[ 1, кПа = 1000, Па ]
Как видно из формулы, давление на поверхность зависит от площади поверхности. Так, человек проваливается в снег при ходьбе по нему и спокойно перемещается на лыжах. В том случае, когда нужно увеличить давление на твёрдое тело, используют заострённые предметы, например, булавки, гвозди, ножи и т.п.
2. Жидкости и газы тоже оказывают давление на сосуд, в котором они находятся. Так, молекулы газа, находящегося в воздушном шаре, непрерывно движутся и при этом соударяются со стенками шара. Эти удары и вызывают давление газа на стенки шара и любого другого сосуда, в котором газ находится. Удар одной молекулы слаб, но внутри шара находится огромное число молекул, поэтому
их суммарное давление на стенки шара ощутимо.
Чем выше температура газа, чем с большей скоростью движутся молекулы и чем чаще и сильнее ударяются они о стенки сосуда, тем, следовательно, давление газа на стенки сосуда больше.
Если уменьшить объём газа в сосуде, не меняя его массу, то число молекул в единице объёма увеличится, увеличится и плотность газа. Число ударов молекул о стенки сосуда при этом возрастёт, следовательно, увеличится давление газа. При увеличении объёма газа при той же массе уменьшится его плотность и число ударов молекул о стенки сосуда. Давление уменьшится.
Таким образом, давление газа тем больше, чем выше его температура и меньше объём при неизменной массе. При повышении температуры и уменьшении объёма молекулы с большей силой и чаще ударяются о стенки сосуда.
3. Опыт показывает, что давление, производимое на жидкость или газ, передаётся по всем направлениям. Если шар с отверстиями, соединённый с трубкой, внутри которой находится поршень, наполнить водой, а затем нажать на поршень, то можно заметить, что вода брызнет из всех отверстий. При этом струйки вытекающей воды будут примерно одинаковыми. Это говорит о том, что давление, которое мы создаём, действуя на воду, передаётся водой по всем направлениям одинаково. Тот же эффект можно наблюдать, если шар заполнить дымом. Дым тоже будет передавать производимое на него давление по всем направлениям одинаково.
То, что газы и жидкости передают давление по всем направлениям, объясняется подвижностью их молекул. Она проявляется в том, что слои и частицы жидкостей и газов могут свободно перемещаться друг относительно друга но разным направлениям. Благодаря подвижности молекул давление, которое оказывает поршень на ближайший к нему слой, передаётся последующим слоям. Молекулы газа и жидкости движутся хаотически, поэтому и их действие распределяется равномерно по всему объёму шара. Таким образом, давление, производимое на жидкость или газ, передаётся по всем направлениям без изменения в каждую точку жидкости или газа. Это утверждение называется законом Паскаля.
4. Закон Паскаля находит применение в гидравлических машинах.
Основной частью любой гидравлической машины являются два соединенных между собой цилиндра разного диаметра. Цилиндры заполнены жидкостью, чаще всего маслом, и в них помещены поршни.
Пусть на большой поршень площадью ( S_1 ) действует сила ( F_1 ) (рис. 56). Эта сила будет оказывать на поршень давление ( p_1 ): ( p_1=F_1/S_1 ).
Это давление ( p_1 ) будет передаваться жидкости, находящейся под большим поршнем. Согласно закону Паскаля, давление, производимое на жидкость или газ, передаётся по всем направлениям без изменения. Следовательно, давление будет передаваться жидкости, находящейся под меньшим поршнем, и на меньший поршень со стороны жидкости будет действовать давление ( p_2=p_1 ). Соответственно, на меньший поршень со стороны жидкости будет действовать сила ( F_2=p_2S_2 ), направленная вверх. Откуда ( p_2=F_2/S_2 ).
Чтобы жидкость и поршни находились в равновесии, на меньший поршень следует подействовать силой, равной по модулю силе ( F_2 ), направленной вертикально вниз. Для этого можно, например, положить на поршень груз.
Так как ( p_1=p_2 ), то ( F_1/S_1=F_2/S_2 ) или ( F_1/F_2=S_1/S_2 ).
Таким образом, гидравлическая машина даёт выигрыш в силе во столько раз, во сколько раз площадь большего поршня больше площади меньшего поршня.
Это означает, что с помощью некоторой силы, приложенной к малому поршню гидравлической машины, можно уравновесить существенно большую силу, приложенную к большему поршню.
Гидравлическая машина, так же как и любой простой механизм, даёт выигрыш в силе, но не даёт выигрыша в работе.
5. Твёрдые тела производят давление на опору вследствие действия на них силы тяжести. Поскольку на жидкости тоже действует сила тяжести, то и жидкости оказывают давление на дно сосуда. Это можно доказать экспериментально.
Если в трубку, дно которой затянуто плёнкой, налить воду, то плёнка заметно прогнётся. Это происходит потому, что на воду действует сила тяжести, и каждый слой воды давит на слои воды, лежащие ниже, и соответственно на дно сосуда.
Давление производится жидкостью не только на дно сосуда, оно существует внутри жидкости на любой её глубине. При этом производимое давление передаётся по закону Паскаля по всем направлениям одинаково.
Если в трубку с дном, затянутым плёнкой, добавить воды, то плёнка прогнётся сильнее. Это происходит потому, что увеличивается вес воды и соответственно давление воды на дно трубки. Таким образом, давление жидкости на дно сосуда тем больше, чем больше высота столба жидкости.
Если теперь в трубку до той же высоты налить масло, плотность которого меньше плотности воды, то плёнка прогнётся меньше, чем в том случае, когда в ней была вода (рис. 57 а). Это означает, что давление на дно сосуда тем больше, чем больше плотность жидкости.
Сила ( F ), с которой жидкость давит на дно, равна её весу ( P ). Вес жидкости ( P ) равен произведению её массы ( m ) и ускорения свободного падения ( g ): ( F=P=mg ).
Масса жидкости ( m ) равна произведению её плотности ( rho ) и объёма ( V ): ( m=rho V ), где ( V=Sh ) (рис. 57 б). Тогда ( F=mg=rho V!g=rho Shg ).
Разделив вес жидкости (силу, с которой она давит на дно сосуда) на площадь дна, получим давление жидкости ( p ): ( p=F/S ) или ( p=rho gSh/S ), т.е. ( p=rho gh )
Давление жидкости на дно и стенки сосуда равно произведению плотности жидкости, ускорения свободного падения и высоты столба жидкости.
6. Два или более сосудов, соединённых между собой у дна, называются сообщающимися сосудами. Примерами сообщающихся сосудов могут служить гидравлические машины и жидкостный манометр. Самым простым сообщающимся сосудом, которым вы пользуетесь каждый день, является чайник.
Если две стеклянные трубки соединить резиновой трубкой (рис. 57 в), то получатся сообщающиеся сосуды. Наливая в одну трубку воду, можно заметить, что она будет перетекать и в другую трубку. При этом уровни воды в трубках будут все время одинаковы.
Можно поднять одну из трубок или наклонить ее, в любом случае друг относительно друга уровни воды или любой другой жидкости останутся одинаковыми, т.е. будут лежать в одной и той же горизонтальной плоскости.
Можно сделать вывод: в сообщающихся сосудах поверхности однородной жидкости всегда устанавливаются на одном уровне.
Это верно при условии, что давление на поверхность жидкости одинаково. При использовании сообщающихся сосудов в качестве жидкостного манометра именно по разности уровней жидкости в трубках можно судить о значении давления.
Объяснить то, что в сообщающихся сосудах однородная жидкость устанавливается на одном уровне, можно следующим образом. Жидкость в сосудах не перемещается, следовательно, её давления в сосудах на одном уровне, в том числе и на дно, одинаковы. Она имеет одинаковую плотность, т.к. она однородная. Следовательно, в соответствии с формулой ( p=rho gh ) высоты жидкости тоже одинаковы.
Если в одну трубку налить воду, а в другую масло, плотность которого меньше плотности воды, то уровень воды будет ниже, чем уровень масла в другой трубке (рис. 58).
Это объясняется тем, что давление жидкости на дно сосуда зависит от высоты столба жидкости и от её плотности. При одинаковом давлении, чем больше плотность жидкости, тем меньше высота её столба. Поскольку плотность масла меньше плотности воды, то столб масла выше столба воды. Жидкости, имеющие разную плотность, устанавливаются в сообщающихся сосудах на разных уровнях; во сколько раз плотность одной жидкости больше плотности другой, во столько раз меньше высота её столба.
7. Земля окружена воздушной оболочкой – атмосферой. Воздух, как и газы, входящие в состав атмосферы, имеет массу. Соответственно, на него действует сила тяжести, и он оказывает давление на поверхность Земли.
Давление воздушной оболочки на поверхность Земли и находящиеся на ней тела называется атмосферным давлением.
В существовании атмосферного давления легко убедиться на опытах. Если опустить в воду трубку с плотно прилегающим к её стенкам поршнем и поднимать поршень вверх, то вода будет подниматься по трубке вслед за поршнем.
Это происходит потому, что при подъёме поршня между ним и поверхностью воды образуется разреженное пространство. На поверхность воды в сосуде действует атмосферное давление, которое в соответствии с законом Паскаля передаётся по всем направлениям, в том числе и в направлении трубки. Оно и заставляет воду подниматься за поршнем.
Для расчёта атмосферного давления нельзя использовать формулу, по которой рассчитывается давление столба жидкости, так как для этого нужно знать высоту атмосферы и плотность воздуха. Но атмосфера не имеет определённой границы, а плотность воздуха изменяется с высотой. Однако атмосферное давление можно измерить.
Опыт по измерению атмосферного давления был предложен итальянским ученым Торричелли в XVII в. Стеклянную трубку длиной 1 м, запаянную с одного конца, заполнили ртутью. Закрыв другой конец трубки, её перевернули и опустили в сосуд с ртутью. Затем этот конец трубки открыли, и часть ртути вылилась из неё в сосуд, а часть осталась в трубке. Высота столба ртути, оставшейся в трубке, оказалась равной примерно 760 мм.
Объясняется это следующим образом: атмосферное давление действует на ртуть в сосуде, это давление передаётся по всем направлениям и действует на ртуть в основании трубки снизу вверх. Это давление уравновешивает давление столба ртути в трубке. Таким образом, атмосферное давление равно давлению, которое оказывает у основании трубки столб ртути высотой 760 мм. Это давление называют нормальным атмосферным давлением.
Если атмосферное давление выше нормального, то высота столба ртути больше, если – меньше нормального, то столб ртути опустится ниже.
Нормальное атмосферное давление равно 101 300 Па.
Атмосферное давление чаще выражают не в паскалях, а в миллиметрах ртутного столба (мм рт.ст.). 1 мм рт.ст. = 133,3 Па.
Если к трубке в опыте Торричелли прикрепить шкалу и проградуировать её в миллиметрах, то получим прибор – ртутный барометр, с помощью которого можно измерять атмосферное давление.
В быту и технике для измерения атмосферного давления применяют более удобный в обращении металлический барометр, называемый анероидом.
Атмосферное давление зависит от высоты. Это объясняется тем, что воздух хорошо сжимаем, так же как и все газы. Верхние слои воздуха давят на лежащие ниже и сжимают их, соответственно плотность слоёв воздуха, а следовательно и давление, у поверхности Земли больше, чем на некоторой высоте от неё.
Так, в местности, лежащей на уровне моря, давление равно примерно 760 мм рт. ст., т.е. нормальному атмосферному. В горах оно выше. Измерения показывают, что на каждые 12 м подъёма атмосферное давление уменьшается примерно на 1 мм рт.ст.
8. Если подвешенный к пружине динамометра шарик опустить в сосуд с водой, то можно заметить, что показание динамометра уменьшится.
Точно так же можно изменить показания динамометра, если подействовать на шарик рукой снизу вверх. Следовательно, когда шарик опустили в воду, на него, помимо силы тяжести и силы упругости пружины динамометра, стала действовать сила, направленная вверх. Эту силу называют выталкивающей или архимедовой силой.
Выталкивающая сила возникает за счёт разности давления воды на нижнюю поверхность шарика и давления на его верхнюю поверхность, поскольку давление жидкости зависит от высоты её столба.
Сила давления ( F_1 ), действующая на верхнюю поверхность шарика, направлена вниз, сила давления ( F_2 ), действующая на нижнюю поверхность шарика, направлена вверх. Так как ( F_2 ) больше ( F_1 ), то результирующая этих двух сил, являющаяся выталкивающей силой, будет направлена вверх.
Выталкивающая сила тем больше, чем больше плотность жидкости, в которую погружено тело, и чем больше объём тела, погружённого в жидкость.
Опыт показывает, что выталкивающая сила ( F ) может быть вычислена по формуле: ( F=rho gV ), где ( rho ) – плотность жидкости, в которую погружено тело, ( V ) – объём погружённой части тела.
Выталкивающая сила равна произведению плотности жидкости, ускорения свободного падения и объёма погружённой части тела.
Этот закон называют законом Архимеда.
В воздухе, так же как и в любом другом газе, на тело действует выталкивающая сила. Она имеет ту же природу, что и выталкивающая сила, действующая на тело в жидкости. Её происхождение обусловлено разностью давлений на нижнюю и верхнюю грани тела. Однако, поскольку плотность газа намного меньше плотности жидкости, выталкивающая сила, действующая на тело, в газе меньше, чем в жидкости. Часто при решении задач пренебрегают выталкивающей силой, действующей на тело в воздухе, и считают, что вес покоящегося тела в воздухе равен по модулю действующей на него силе тяжести.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Ребёнка везут на санках по свежевыпавшему снегу. Какие санки – с широкими или узкими полозьями – следует выбрать, чтобы не проваливаться в снег?
1) с широкими
2) с узкими
3) безразлично
4) ответ зависит от веса санок
2. Брусок в форме прямоугольного параллелепипеда положили на стол сначала узкой гранью (1), а затем – широкой (2). Сравните силы давления (( F_1 ) и ( F_2 )) и давления (( p_1 ) и ( p_2 )), производимые бруском на стол в этих случаях.
1) ( F_1=F_2; p_1>p_2 )
2) ( F_1=F_2; p_1<p_2 )
3) ( F_1<F_2; p_1<p_2 )
4) ( F_1=F_2; p_1=p_2 )
3. Сила ( F_1 ), действующая со стороны жидкости на один поршень гидравлической машины, в 16 раз меньше силы ( F_2 ), действующей на другой поршень. Как соотносятся модули работы ( (A_1) ) и ( (A_2) ) этих сил, совершаемой при перемещении поршней? Трением пренебречь.
1) ( A_1=A_2 )
2) ( A_1=16A_2 )
3) ( A_2=16A_1 )
4) ( A_1=4A_2 )
4. В сосуды различной формы налита одна и та же жидкость. Высота уровня жидкости во всех сосудах одинакова. В каком из сосудов давление на дно наименьшее?
1) в сосуде А
2) в сосуде Б
3) в сосуде В
4) во всех сосудах одинаковое
5. Стеклянный сосуд, правое колено которого запаяно, заполнен жидкостью плотностью с (см. рисунок). Давление, оказываемое жидкостью на дно сосуда в точке Б, равно
1) ( rho gh_3 )
2) ( rho gh_1 )
3) ( rho g(h_1-h_2) )
4) ( rho gh_2 )
6. Атмосферное давление на вершине горы Казбек
1) меньше, чем у её подножия
2) больше, чем у её подножия
3) равно давлению у её подножия
4) может быть больше или меньше, чем у её подножия, в зависимости от погоды
7. В открытых сосудах 1 и 2 находятся соответственно ртуть и вода. Если открыть кран К, то
1) ни вода, ни ртуть перетекать не будут
2) вода начнёт перетекать из сосуда 2 в сосуд 1
3) перемещение жидкостей будет зависеть от атмосферного давления
4) ртуть начнёт перетекать из сосуда 1 в сосуд 2
8. Два однородных шара, один из которых изготовлен из стали, а другой – из олова, уравновешены на рычажных весах (см. рисунок). Нарушится ли равновесие весов,
если шары опустить в воду?
1) Равновесие весов не нарушится, так как шары одинаковой массы.
2) Равновесие весов нарушится – перевесит шар из стали.
3) Равновесие весов нарушится – перевесит шар из олова.
4) Равновесие весов не нарушится, так как шары опускают в одну и ту же жидкость.
9. Алюминиевый шар, подвешенный на нити, опущен в крепкий раствор поваренной соли. Затем шар перенесли из раствора поваренной соли в дистиллированную воду. При этом сила натяжения нити
1) может остаться неизменной или измениться в зависимости от объёма шара
2) не изменится
3) увеличится
4) уменьшится
10. Теплоход переходит из устья реки в солёное море. При этом архимедова сила, действующая на теплоход,
1) увеличится
2) уменьшится или увеличится в зависимости от размера теплохода
3) не изменится
4) уменьшится
11. Шарик, опущенный в жидкость, начинает опускаться на дно. Как по мере движения шарика в жидкости изменяются выталкивающая сила, действующая на него, вес шарика, давление жидкости? Установите соответствие между физическими
