Давление газа на стенки сосуда возникает в результате

Мякишев Г.Я. Давление газа в сосуде //Квант. — 1987. — № 9. — С. 41-42.

По специальной договоренности с редколлегией и редакцией журнала “Квант”

Зависит ли давление газа на стенку сосуда от материала стенки и ее температуры? Попробуем ответить на этот вопрос.

При выводе основного уравнения молекулярно-кинетической теории идеального газа в учебнике «Физика 9» (§7) предполагается, что стенка абсолютно гладкая и столкновения молекул со стенкой происходят по закону абсолютно упругого удара. Другими словами, кинетическая энергия молекулы при ударе не меняется, и угол падения молекулы равен углу отражения. Является ли это предположение оправданным и необходимым?

Коротко можно сказать так: предположение оправдано, но не необходимо.

На первый взгляд кажется, что считать стенку абсолютно гладкой ни в коем случае нельзя — стенка сама состоит из молекул и, значит, гладкой быть не может. Из-за этого угол падения .не может при любом соударении равняться углу отражения. Кроме того, молекулы стенки совершают хаотические колебания около положений равновесия (участвуют в беспорядочном тепловом движении). Поэтому при столкновении с какой-либо молекулой стенки молекула газа может передать часть энергии стенке или, наоборот, увеличить свою кинетическую энергию за счет стенки.

Тем не менее предположение об абсолютно упругом характере соударения молекулы газа со стенкой оправдано. Дело в том, что при вычислении давления в конечном счете важны средние значения соответствующих величин. При условии теплового равновесия между газом и стенкой сосуда кинетическая энергия молекул газа в среднем остается неизменной, т. е. соударения со стенкой не меняют среднюю энергию молекул газа. Если бы это было не так, то тепловое равновесие самопроизвольно нарушалось бы. А это невозможно согласно второму закону термодинамики. Также не может быть преимущественного отражения молекул в каком-либо определенном направлении — иначе сосуд с газом начал бы двигаться, что противоречит закону сохранения импульса. Значит, среднее число молекул, падающих на стенку под некоторым углом, равно среднему числу молекул, отлетающих от стенки под таким же углом. Предположение о зеркальном отражении от стенки каждой отдельной молекулы соответствует этому условию.

Таким образом, считая соударения молекул газа со стенкой упругими, мы получаем для среднего давления такой же результат, как и без этого предположения. Значит, давление газа не зависит от качества обработки стенки (ее гладкости). Однако предположение об абсолютно упругом характере удара сильно упрощает вычисление давления газа, и поэтому оно оправдано.

А зависит ли давление газа на стенку от ее температуры? На первый взгляд — должно зависеть. Если, например, нет теплового равновесия, то молекулы от холодной стенки должны отскакивать с меньшей энергией, чем от горячей.

Однако, даже если одну стенку поддерживать холодной с помощью холодильной установки, то давление на нее все равно не может быть меньше, чем давление на противоположную горячую стенку. Ведь тогда сосуд начал бы двигаться ускоренно без внешних сил, а это противоречит законам механики: освободив закрепленный сосуд со стенками различной температуры, мы не вызовем его смещения. Дело здесь в том, что при данном неравновесном состоянии газа в сосуде концентрация молекул у холодной стенки больше, чем у горячей. Уменьшение кинетической энергии молекул у холодной стенки компенсируется увеличением концентрации молекул и наоборот. В результате давление на холодную и горячую стенки оказывается одним и тем же.

Рассмотрим еще один вариант опыта. Охладим очень быстро одну из стенок. В первый момент давление на нее уменьшится, и сосуд немного сдвинется с места; затем давления выравняются, и сосуд остановится[1]. Но при этом движении центр масс системы останется на месте из-за того, что плотность газа у холодной стенки станет чуть больше, чем у горячей.

Следует отметить, что на самом деле давление не остается строго фиксированной величиной. Оно испытывает флуктуации, и поэтому сосуд слегка «дрожит» на месте. Но амплитуда дрожания сосуда крайне мала.

Итак, окончательно мы пришли к выводу, что давление газа на стенки в сосуде не зависит ни от качества обработки стенок, ни от их температуры.

Примечания

1. ↑ Остановка сосуда произойдет из-за того, что молекулы газа при ударе передают больший импульс той стенке, которая движется им навстречу.

Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.

Идеальные газы

Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.

В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.

В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.

Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.

Причина возникновения давления в газах

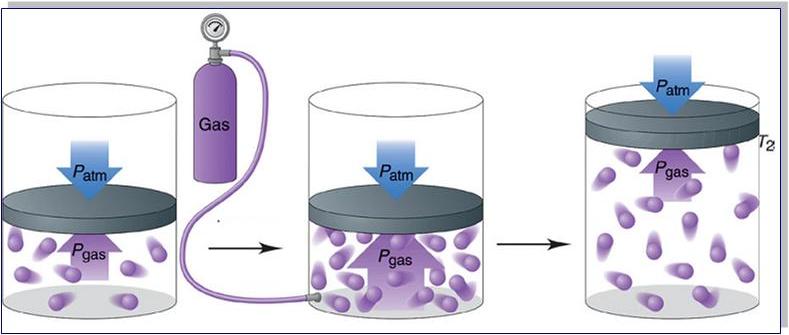
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.

Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:

P = F/S

Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:

F*Δt = Δp

Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.

Формула давления газа идеального из молекулярно-кинетической теории

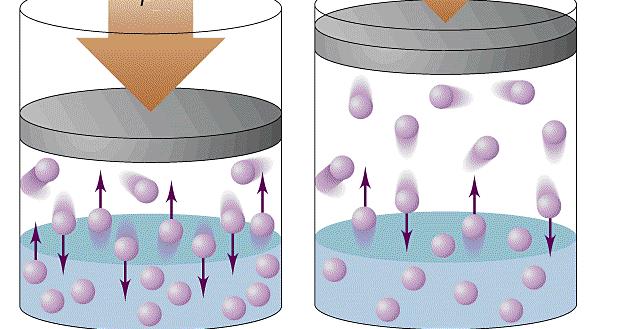
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.

Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.

Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:

P = N*m*v2/(3*V)

Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.

Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:

P*V = n*R*T

Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.

Из уравнения выше легко получить формулу давления газа:

P = n*R*T/V

Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.

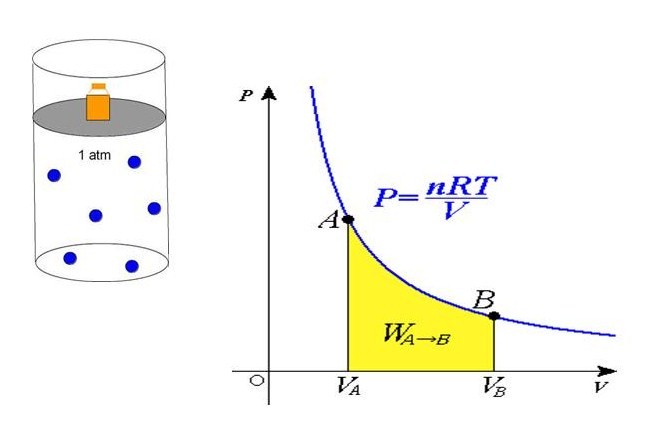
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.

Давление в газовой смеси

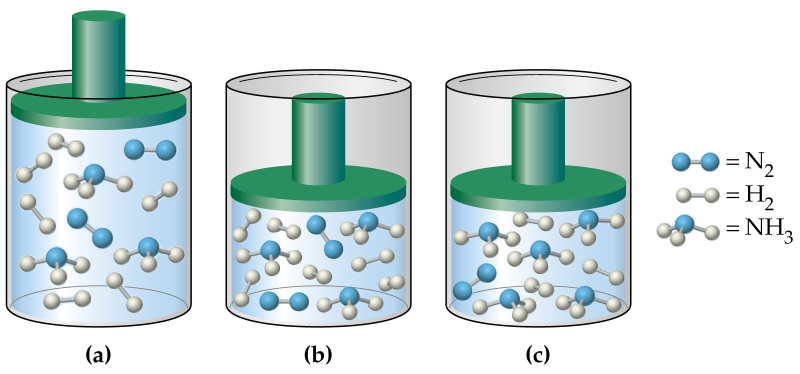
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.

Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:

• Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
• Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.

Пример задачи

Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.

Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:

P = N*m*v2/(3*V)

Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:

m = M/NA;

n = N/NA;

m*N = M*n;

P = M*n*v2/(3*V)

Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.

Макеты страниц

1

Повторим 1. Чем вызвано давление газа на стенки сосуда? 1. Чем вызвано давление газа на стенки сосуда? 2. В чем суть закона Паскаля? 2. В чем суть закона Паскаля?

2

Опыт Объясним?!

3

Атмосферное давление

4

Атмосфера – воздушная оболочка Земли воздушная оболочка Земли простирается на высоту несколько тысяч км простирается на высоту несколько тысяч км масса атмосферы масса атмосферы четкой границы не существует четкой границы не существует

5

Поведение молекул атмосферы Атмосфера состоит из газов, а почему молекулы не улетают в мировое пространство? Атмосфера состоит из газов, а почему молекулы не улетают в мировое пространство? Как все тела, молекулы газов, входящих в состав воздушной оболочки Земли, притягиваются к Земле. Как все тела, молекулы газов, входящих в состав воздушной оболочки Земли, притягиваются к Земле. Чтобы покинуть Землю, они должны обладать скоростью не меньше 11,2 км/с, это вторая космическая скорость. Большинство молекул имеют скорость меньше 11,2 км/с. Чтобы покинуть Землю, они должны обладать скоростью не меньше 11,2 км/с, это вторая космическая скорость. Большинство молекул имеют скорость меньше 11,2 км/с. А почему атмосфера не оседает на поверхность Земли? А почему атмосфера не оседает на поверхность Земли? Молекулы газов, составляющих атмосферу, движутся непрерывно и беспорядочно. Молекулы газов, составляющих атмосферу, движутся непрерывно и беспорядочно.

6

Почему атмосфера оказывает давление на тела, находящиеся на Земле?

7

Под действием силы тяжести верхние слои воздуха атмосферы сжимают нижние. Под действием силы тяжести верхние слои воздуха атмосферы сжимают нижние. Прилегающий к Земле слой сжат больше всего. Прилегающий к Земле слой сжат больше всего. Земная поверхность и тела на ней испытывают давление всей толщи воздуха (по закону Паскаля) –атмосферное давление. Земная поверхность и тела на ней испытывают давление всей толщи воздуха (по закону Паскаля) –атмосферное давление.

8

Доказательство существования веса у воздуха

9

Какие массы воздуха встречаются в нашей жизни

10

Исторический факт Впервые весомость воздуха привела людей в замешательство в 1638 году, когда не удалась затея герцога Тосканского украсить сады Флоренции фонтанами – вода не поднималась выше 10,3м. Впервые весомость воздуха привела людей в замешательство в 1638 году, когда не удалась затея герцога Тосканского украсить сады Флоренции фонтанами – вода не поднималась выше 10,3м. Поиски причин упрямства воды и опыты с более тяжелой жидкостью – ртутью, предпринятые в 1643г. Торричелли, привели к открытию атмосферного давления. Поиски причин упрямства воды и опыты с более тяжелой жидкостью – ртутью, предпринятые в 1643г. Торричелли, привели к открытию атмосферного давления.

11

Опыт Отто фон Герике В 1654 году магдебургский бургомистр и физик Отто фон Герике показал на рейхстаге в Регенсбурге один опыт, который теперь во всём мире называют опытом с магдебургскими полушариями. В 1654 году магдебургский бургомистр и физик Отто фон Герике показал на рейхстаге в Регенсбурге один опыт, который теперь во всём мире называют опытом с магдебургскими полушариями.

12

Опыт в домашних условиях Описание опыта в карточке с домашним заданием

13

Помощники в медицине

14

Атмосферное давление и человек Атмосферное давление не ощущается человеком и животными. Атмосферное давление не ощущается человеком и животными. Ткани, кровяносные сосуды и стенки других полостей тела подвергаются наружному давлению атмосферы. Ткани, кровяносные сосуды и стенки других полостей тела подвергаются наружному давлению атмосферы. Кровь и другие жидкости и газы, заполняющие эти полости, оказывают изнутри такое же давление. Кровь и другие жидкости и газы, заполняющие эти полости, оказывают изнутри такое же давление.

15

Пришло время очередного опыта

16

17

Дыхание Механизм вдоха заключается в следующем: мышечным усилием мы увеличиваем объем грудной клетки, при этом давление воздуха внутри легких становится меньше атмосферного, и атмосферное давление вталкивает порцию воздуха в область меньшего давления. Механизм вдоха заключается в следующем: мышечным усилием мы увеличиваем объем грудной клетки, при этом давление воздуха внутри легких становится меньше атмосферного, и атмосферное давление вталкивает порцию воздуха в область меньшего давления. Как происходит выдох? Как происходит выдох?

18

Домашнее задание Интересная информация на сайте Классная физика Можно ответить на вопросы на отдельную оценку Интересная информация на сайте Классная физика Можно ответить на вопросы на отдельную оценку §40 §40 Заполнить карточку Заполнить карточку Проделать и объяснить письменно один из опытов Проделать и объяснить письменно один из опытов

19

Почему пассажирам самолетов перед подъемом рекомендуется удалить чернила из авторучек? Почему пассажирам самолетов перед подъемом рекомендуется удалить чернила из авторучек? Как стеклянную трубочку набрать воду? Как стеклянную трубочку набрать воду? Зачем в крышках бидонов для смазочных масел делают не одно, а два отверстия? Зачем в крышках бидонов для смазочных масел делают не одно, а два отверстия? Зачем в крышке фарфорового чайника делают отверстие? Зачем в крышке фарфорового чайника делают отверстие? Почему трудно вытащить ноги, увязшие в размокшей глине? Почему трудно вытащить ноги, увязшие в размокшей глине? Кому легче ходить по грязи? Лошади, имеющей сплошное копыто, очень трудно вытащить ногу из глубокой грязи. Под ногой, когда она ее поднимает, образуется разреженное пространство и атмосферное давление препятствует вытаскиванию ноги. В этом случае нога работает как поршень в цилиндре. Лошади, имеющей сплошное копыто, очень трудно вытащить ногу из глубокой грязи. Под ногой, когда она ее поднимает, образуется разреженное пространство и атмосферное давление препятствует вытаскиванию ноги. В этом случае нога работает как поршень в цилиндре. Внешнее, огромное по сравнению с возникшим, атмосферное давление не дает поднять ногу. При этом сила давления на ногу может достигать 1000 Н. Внешнее, огромное по сравнению с возникшим, атмосферное давление не дает поднять ногу. При этом сила давления на ногу может достигать 1000 Н. Намного легче передвигаться по такой грязи жвачным животным, у которых копыта состоят из нескольких частей и при вытаскивании ноги из грязи сжимаются, пропуская воздух в образовавшееся углубление. Намного легче передвигаться по такой грязи жвачным животным, у которых копыта состоят из нескольких частей и при вытаскивании ноги из грязи сжимаются, пропуская воздух в образовавшееся углубление.

20

Атмосферное давление и погода Атмосферное давление помогает предсказывать погоду, что необходимо людям разных профессий – летчикам, агрономам, радистам, полярникам, медикам, ученым. Если атмосферное давление повышается, то погода будет хорошей: холодной – зимой, жаркой – летом; если резко падает, то можно ожидать появления облачности, насыщения воздуха влагой. Понижение давления летом предвещает похолодание, зимой – потепление. Атмосферное давление помогает предсказывать погоду, что необходимо людям разных профессий – летчикам, агрономам, радистам, полярникам, медикам, ученым. Если атмосферное давление повышается, то погода будет хорошей: холодной – зимой, жаркой – летом; если резко падает, то можно ожидать появления облачности, насыщения воздуха влагой. Понижение давления летом предвещает похолодание, зимой – потепление. Атмосферное давление увеличивается, если будут происходить перемещения масс воздуха вниз (нисходящие потоки). Опускается с больших высот сухой воздух, поэтому погода будет хорошей, без осадков. Понижается же атмосферное давление при восходящих потоках воздуха. Вверх поднимается воздух, обильно насыщенный водяными парами. Вверху он охлаждается, что приводит к появлению облачности, выпадению осадков – погода при этом ухудшается. Атмосферное давление увеличивается, если будут происходить перемещения масс воздуха вниз (нисходящие потоки). Опускается с больших высот сухой воздух, поэтому погода будет хорошей, без осадков. Понижается же атмосферное давление при восходящих потоках воздуха. Вверх поднимается воздух, обильно насыщенный водяными парами. Вверху он охлаждается, что приводит к появлению облачности, выпадению осадков – погода при этом ухудшается.

21

Что произошло бы на Земле, если бы воздушная атмосфера вдруг исчезла? на Земле установилась бы температура приблизительно С на Земле установилась бы температура приблизительно С замерзли бы все водные пространства, а суша покрылась бы ледяной корой замерзли бы все водные пространства, а суша покрылась бы ледяной корой наступила бы полная тишина, так как звук в пустоте не распространяется наступила бы полная тишина, так как звук в пустоте не распространяется небо стало бы черным, поскольку окраска небесного свода зависит от воздуха; не стало бы сумерек, зорь, белых ночей небо стало бы черным, поскольку окраска небесного свода зависит от воздуха; не стало бы сумерек, зорь, белых ночей прекратилось бы мерцание звезд, а сами звезды были бы видны не только ночью, но и днем (днем мы их не видим из-за рассеивания частичками воздуха солнечного света) прекратилось бы мерцание звезд, а сами звезды были бы видны не только ночью, но и днем (днем мы их не видим из-за рассеивания частичками воздуха солнечного света) погибли бы животные и растения погибли бы животные и растения