Давление газа на стенки сосуда вызывается
Глава 3. Давление твёрдых тел, жидкостей и газов
Мы уже знаем, что газы, в отличие от твёрдых тел и жидкостей, заполняют весь сосуд, в котором они находятся. Например, стальной баллон для хранения газов, камера автомобильной шины или волейбольный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твёрдого тела на опору.
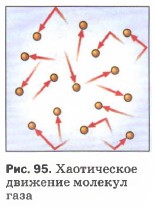
Известно, что молекулы газа беспорядочно движутся. При своём движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ (рис. 95). Молекул в газе много, потому и число их ударов очень велико. Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см2 за 1 с выражается двадцатитрёхзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, оно и создаёт давление газа.
Итак, давление газа на стенки сосуда (и на помещённое в газ тело) вызывается ударами молекул газа.

Рассмотрим следующий опыт. Под колокол воздушного насоса помещают завязанный резиновый шарик. Он содержит небольшое количество воздуха (рис. 96, а) и имеет неправильную форму. Затем насосом откачивают воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится всё более разреженным, постепенно раздувается и принимает форму шара (рис. 96, б).
Как объяснить этот опыт?
В нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул в колоколе вокруг оболочки шарика уменьшается. Но внутри завязанного шарика их число не изменяется. Поэтому число ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его резиновой оболочки не станет равной силе давления газа. Оболочка шарика принимает форму шара. Это показывает, что газ давит на её стенки по всем направлениям одинаково. Иначе говоря, число ударов молекул, приходящихся на каждый квадратный сантиметр площади поверхности, по всем направлениям одинаково. Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.

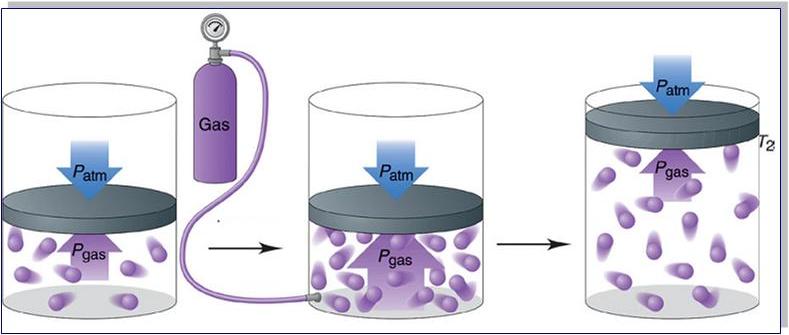
Попытаемся уменьшить объём газа, но так, чтобы масса его осталась неизменной. Это значит, что в каждом кубическом сантиметре газа молекул станет больше, плотность газа увеличится. Тогда число ударов молекул о стенки сосуда возрастёт, т. е. возрастёт давление газа. Это можно подтвердить опытом.
На рисунке 97, а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой плёнкой. В трубку вставлен поршень. При вдвигании поршня объём воздуха в трубке уменьшается, т. е. газ сжимается (рис. 97, б). Резиновая плёнка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.
Наоборот, при увеличении объёма этой же массы газа число молекул в каждом кубическом сантиметре уменьшится. От этого уменьшится число ударов о стенки сосуда — давление газа станет меньше. Действительно, при вытягивании поршня из трубки объём воздуха увеличивается, плёнка прогибается внутрь сосуда (рис. 97, в). Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился любой другой газ.
Итак, при уменьшении объёма газа его давление увеличивается, а при увеличении объёма давление уменьшается при условии, что масса и температура газа остаются неизменными.

А как изменится давление газа, если нагреть его при постоянном объёме? Известно, что скорость движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку сосуда станет сильнее. Вследствие этого стенки сосуда будут испытывать большее давление.
Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объём не изменяются.
Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.
Для хранения и перевозки газов их сильно сжимают. При этом давление их возрастает, газы приходится заключать в специальные, очень прочные стальные баллоны (рис. 98). В таких баллонах, например, содержат сжатый воздух в подводных лодках, кислород, используемый при сварке металлов.
Вопросы
1. Какие свойства газов отличают их от твёрдых тел и жидкостей?
2. Как объясняют давление газа на основе учения о движении молекул?
3. Как можно на опыте показать, что газ производит давление на стенки сосуда, в котором он находится?
4. Из чего можно заключить, что газ производит одинаковое давление по всем направлениям?
5. Почему давление газа увеличивается при сжатии и уменьшается при расширении?
6. Почему сжатые газы содержат в специальных баллонах?
Задание
Надуйте воздушный шарик и крепко его завяжите. Положите в любую ёмкость. Вначале облейте его водой, охлаждённой в морозильной камере (до 5°С), затем горячей водой (70°С). Дайте объяснение наблюдаемому явлению.
Источник
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
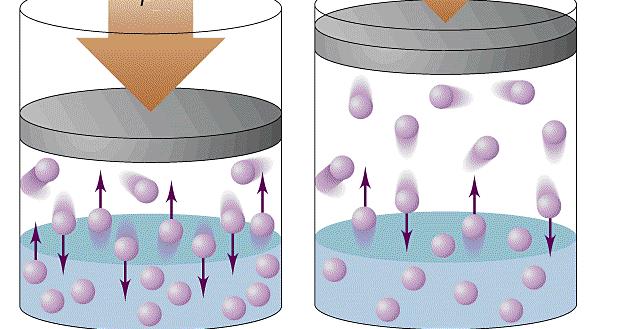
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
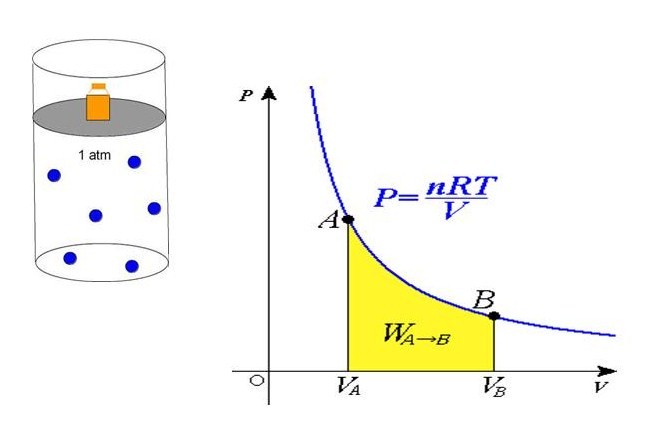
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
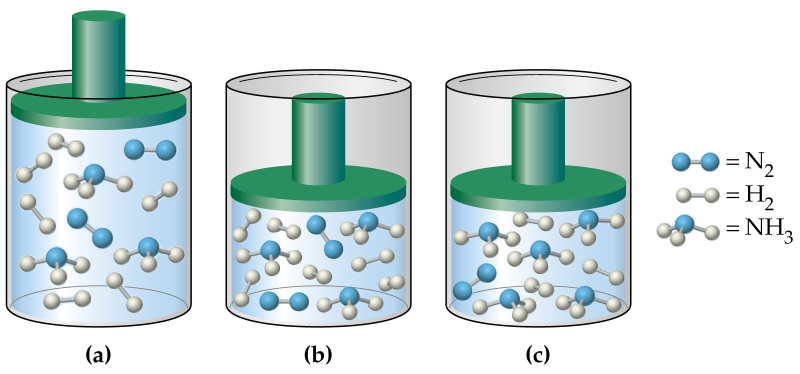
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Давление газа на стенки сосуда вызывается:
ударами молекул |
расстоянием между молекулами газа |
воздухом внутри |
нет однозначного ответа |
С глубиной давление:
увеличивается |
уменьшается |
не изменяется |
нет однозначного ответа |
Впишите ответ.
Переведите давление 645 кПа в Па.
645 кПа =
Па
Где используется закон Паскаля?
При забивании гвоздя в стену |
При шитье иголкой |
При закачке воздуха в шины автомобиля |
При игре в компьютер |
Впишите в текст пропущенные слова.
Для того чтобы
газа, надо либо
количество
молекул о стенки сосуда, либо увеличить
этих ударов, либо сделать то и другое
.
От чего зависит давление газа?
от объёма
от температуры
от массы газа
от цвета газа
Газ в сосуде сжимают поршнем. Как при этом меняется давление газа внутри сосуда?
увеличивается |
уменьшается |
не изменяется |
нет однозначного ответа |
Для того чтобы давление газа, содержащегося в определённом объёме, не изменялось при его подогреве, необходимо:
выпустить часть газа или уменьшить его объём |
добавить некоторое количество газа или увеличить его объём |
выпустить часть газа или увеличить его объём |
добавить некоторое количество газа или уменьшить его объём |
Источник
Мы
знаем, что газы, в отличие от твёрдых
тел и жидкостей заполняют весь сосуд,
в котором они находятся, например
стальной баллон для хранения газов,
камеру автомобильной шины или волейбольного
мяча. При этом газ оказывает давление
на стенки, дно и крышку баллона, камеры
или любого другого тела, в котором он
находится. Давление газа обусловлено
иными причинами, чем давление твёрдого
тела на опору. Известно, что молекулы
газа беспорядочно движутся. При своём
движении они сталкиваются друг с другом,
а также со стенками сосуда, в котором
находится газ. Молекул в газе много,
потому и число их ударов очень велико.
Хотя сила удара отдельной молекулы
мала, но действие всех молекул о стенки
сосуда значительно, оно и создаёт
давление газа. Итак, давление газа на
стенки сосуда (и на помещённое в газ
тело) вызывается ударами молекул газа.
При уменьшении объёма газа его давление
увеличивается, а при увеличении объёма
давление уменьшается при условии, что
масса и температура газа остаются
неизменными. Давление газа в закрытом
сосуде тем больше, чем выше температура
газа, при условии, что масса газа не
меняется.
27. Средняя кинетическая энергия поступательного движения молекул идеального газа.
Средняя
кинетическая энергия поступательного
движения молекулы идеального газа
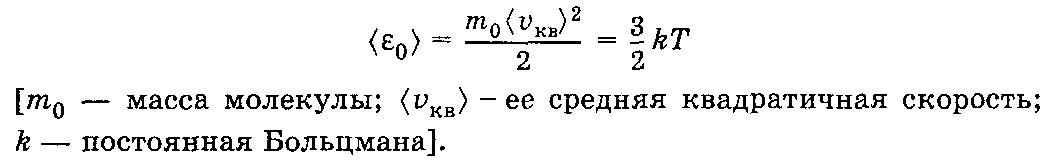
28. Распределение Максвелла. Виды скоростей молекул и их физический смысл.
Распределение
Максвелла
Молекулы
газа вследствие теплового движения
испытывают многочисленные соударения
друг с другом. При каждом соударении
скорости молекул изменяются как по
величине, так и по направлению. В
результате в сосуде, содержащем большое
число молекул, устанавливается некоторое
статистическое распределение молекул
по скоростям, зависящее от абсолютной
температуры Т. При этом все направления
векторов скоростей молекул оказываются
равноправными (равновероятными), а
величины скоростей подчиняются
определенной закономерности. Распределение
молекул газа по величине скоростей
называется распределением Максвелла.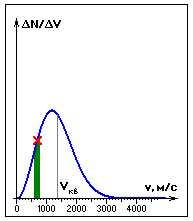
Если
одновременно измерить скорости большого
числа N молекул газа и выделить некоторый
малый интервал скоростей от v до v+![]() v,
v,
то в выделенный интервал![]() v
v
попадает некоторое число![]() N
N
молекул. На графике удобно изображать
зависимость величины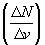 от
от
скорости v. При достаточно большом числе
N эта зависимость изображается плавной
кривой, имеющей максимум при![]() (наиболее
(наиболее
вероятная скорость). Здесь m – масса
молекулы,![]() –
–
постоянная Больцмана.
Характерным
параметром распределения Максвелла
является так называемая среднеквадратичная
скорость ![]() означает
означает
среднее значение квадрата скорости. В
молекулярной физике доказывается, что
![]()
где ![]() –
–
молярная масса.
Из выражения
для среднеквадратичной скорости следует,
что средняя кинетическая энергия
поступательного движения молекул газа
есть
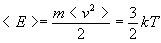
Распределение
Максвелла является одной из важнейших
статистических закономерностей
молекулярной физики.
Скорости
молекул подразделяются на:
1)
наиболее вероятную 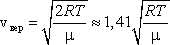 ,
,
2)
среднюю 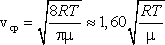 ,
,
3)
среднюю квадратичную 
29. Распределение Больцмана. Барометрическая формула.
Барометрическая
формула.
Если
температура не зависит от высоты, то
давление газа меняется с высотой по
закону:
![]() ,
,
где![]() —
—
высота,![]() —
—
молярная газовая постоянная,![]() —
—
постоянная Больцмана,![]() —
—
ускорение свободного падения вблизи
поверхности земли,![]() —
—
молярная масса газа,![]() —
—
масса одной молекулы,![]() —
—
абсолютная температура.
Поделив
барометрическую формулу на ![]() ,
,
с учетом уравнения состояния идеального
газа, получим распределение Больцмана
— зависимость концентрации молекул от
потенциальной энергии:
![]() ,
,
где ![]() —
—
потенциальная энергия молекулы. В
однородном поле силы тяжести ![]() .
.
Exp, как я поняла, это «экспериментальное»???????????????
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
19.05.201525.13 Mб18Учебник по английскому.pdf
- #
- #
- #
- #
- #
- #
- #
- #
Источник
