Давление газа на стенку сосуда средняя энергия молекул
Макеты страниц
Стенки сосуда, в котором заключен газ, подвергаются непрерывной бомбардировке молекулами. В результате элементу стенки сообщается за секунду некоторый импульс, который равен силе, действующей на . Отношение этой силы к величине дает давление, оказываемое газом на стенки сосуда. Вследствие хаотичности движения молекул давление газа на различные участки стенок сосуда одинаково (разумеется, при условии, что газ находится в равновесном состоянии).
Если предположить, что молекулы отскакивают от стенки по закону зеркального отражения величина скорости молекулы не изменяется, то импульс, сообщаемый при ударе стенке молекулой, будет равен (рис. 96.1; — масса молекулы). Этот импульс направлен по нормали к площадке. Каждая из молекул (см. (95.2)) сообщает стенке импульс а все эти молекулы — импульс
Просуммируем полученное выражение по направлениям в пределах телесного угла (отвечающего изменениям Ф от 0 до и изменениям от 0 до .
Рис. 96.1.
В результате получим импульс, сообщаемый молекулами, скорости которых имеют величину от v до
(мы подставили выражение (94.4) для Интегрирование по дает интеграл по равен 1/3. Следовательно,
Проинтегрировав это выражение по скоростям от 0 до получим полный импульс, сообщаемый площадке за время
Выражение
представляет собой среднее значение квадрата скорости молекул. Заменив в (96.1) интеграл произведением получим, что
есть число молекул в единице объема). Наконец, разделив это выражение на и получим давление газа на стенки сосуда:
Масса всех молекул по предположению одинакова. Поэтому ее можно внести под знак среднего. В результате выражение (96.2) примет вид
где — среднее значение кинетической энергии поступательного движения молекул.
Получим выражение для давления, исходя из упрощенных представлений, которые привели нас к формуле (95.7). Согласно этим представлениям каждая молекула сообщает стенке при ударе импульс Умножив этот импульс на число ударов (см. (95.7)), получим импульс, сообщаемый единичной площадке в единицу времени, т. е. давление.
Таким образом, получается формула
Эта формула отличается от (96.2) тем, что вместо среднего квадрата скорости стоит квадрат средней скорости Впоследствии (см. § 97) мы убедимся в том, что эти две величины отличаются друг от друга, т. е.
При более аккуратном подсчете нужно число молекул, определяемое формулой (95.8), умножить на и затем произвести суммирование по всем V. В результате получится импульс, сообщаемый площадке за время
Разделив это выражение на и получим для давления формулу (96-2). Таким образом, исходя из упрощенного представления о движении молекул вдоль трех взаимно перпендикулярных направлений, мы получили точное выражение для давления. Это объясняется тем, что указанное упрощение приводит, с одной стороны, к занижению числа ударов молекул о стенку вместо см. (95.6) и (95.7)), а с другой — к завышению импульса, передаваемого стенке при каждом ударе. При упрощенном выводе мы принимали, что при каждом ударе стенке сообщается импульс, равный . В действительности же величина сообщаемого стенке импульса зависит от угла вследствие чего средний импульс, сообщаемый при одном ударе, равен . В итоге обе неточности взаимно компенсируют друг друга и, несмотря на упрощенность рассмотрения, получается точное выражение для давления.
Источник
Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.
Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:
- все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
- частицы находятся в непрерывном тепловом движении;
- между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.
Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.
Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.
Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.
Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.
Существует еще одно состояние вещества – плазма. Плазма – частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е. молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
Модель идеального газа. Связь между давлением и средней кинетической энергией.
Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.
Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)
Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.
Свойства идеального газа:
- расстояние между молекулами много больше размеров молекул;
- молекулы газа очень малы и представляют собой упругие шары;
- силы притяжения стремятся к нулю;
- взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
- молекулы этого газа двигаются беспорядочно;
- движение молекул по законам Ньютона.
Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.
Объем газа обозначается V. Объем газа всегда совпадает с объемом того сосуда, который он занимает. Единица объема в СИ м3.
Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.
p = F/S Единица давления в СИ паскаль [Па]
До настоящего времени употребляются внесистемные единицы давления:
техническая атмосфера 1 ат = 9,81-104 Па;
физическая атмосфера 1 атм = 1,013-105 Па;
миллиметры ртутного столба 1 мм рт. ст.= 133 Па;
1 атм = = 760 мм рт. ст. = 1013 гПа.
Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени действует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.
Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.
Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной.
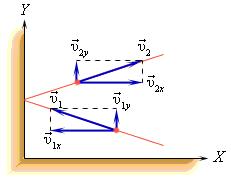
Приборы, измеряющие давление, называют манометрами. Манометры фиксируют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.
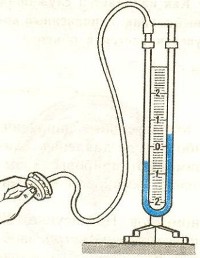
Жидкостные манометры:
- открытый – для измерения небольших давлений выше атмосферного
- закрытый – для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума

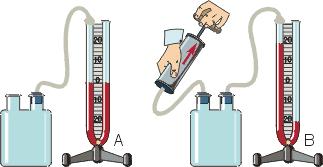
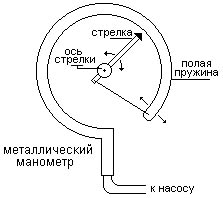
Металлический манометр – для измерения больших давлений.
Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.
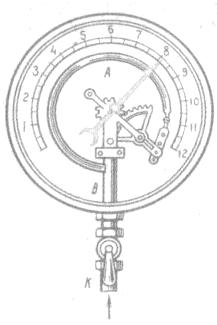
Основное уравнение молекулярно-кинетической теории идеального газа.
Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул
p = 1/3·m0·n·v2
m0 – масса одной молекулы газа;
n = N/V – число молекул в единице объема, или концентрация молекул;
v2 – средняя квадратичная скорость движения молекул.
Так как средняя кинетическая энергия поступательного движения молекул E = m0*v2/2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0· v2)/2 = 2/3·E·n
p = 2/3·E·n
Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
Так как m0·n = m0·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v2
Объединенный газовый закон.
Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Всякое изменение состояния газа называется термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.
Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
p = nkT
Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим или
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.
Уравнение Клайперона можно записать в другой форме.
p = nkT,
учитывая, что
Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
Ее численное значение в СИ R = 8,31 Дж/моль·К
Соотношение
называется уравнением состояния идеального газа.
В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`
Для одного моля любого газа это соотношение принимает вид: pV=RT
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.
Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pSΔh = R
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A.
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.
Источник
Îñíîâíîå óðàâíåíèå ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè óñòàíàâëèâàåò ñâÿçü ìåæäó äàâëåíèåì èäåàëüíîãî ãàçà è ñðåäíåé êèíåòè÷åñêîé ýíåðãèåé åãî ìîëåêóë.
Âûâîä îñíîâíîãî óðàâíåíèÿ ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè îñíîâûâàåòñÿ íà äîïóùåíèÿõ ìîäåëè èäåàëüíîãî ãàçà è óòâåðæäåíèè: äàâëåíèå ãàçà ÿâëÿåòñÿ ðåçóëüòàòîì óäàðîâ ìîëåêóë î ñòåíêó ñîñóäà.
Îïðåäåëèì äàâëåíèå ãàçà íà ñòåíêó ïëîùàäüþ S ñîñóäà ABCD.

Êàæäàÿ ìîëåêóëà ìàññîé m, îòñêàêèâàÿ îò ñòåíêè ïîñëå óïðóãîãî ñîóäàðåíèÿ ñî ñòåíêîé, ïåðåäàåò åé èìïóëüñ 2m0vx, ãäå vx— ïðîåêöèÿ ñêîðîñòè ìîëåêóëû íà îñü Îõ, ïåðïåíäèêóëÿðíóþ ñòåíêå. Âñåãî çà îäíó ñåêóíäó ñóììàðíûé èìïóëüñ, ïîëó÷àåìûé ñòåíêîé îò âñåõ ìîëåêóë, ðàâåí 2m0vxZ, ãäå Z — ÷èñëî òàêèõ ñòîëêíîâåíèé (çà 1 ñ) âñåõ ìîëåêóë. Î÷åâèäíî, ÷òî , ãäå n — êîíöåíòðàöèÿ ìîëåêóë â åäèíèöå îáúåìà; N — ÷èñëî âñåõ ìîëåêóë. ×èñëî Z ïðîïîðöèîíàëüíî òàêæå ñêîðîñòè ìîëåêóë vxè ïëîùàäè ñòåíêè S: Z~ nvxS. Ïîñêîëüêó âñå íàïðàâëåíèÿ ïðè õàîòè÷íîì äâèæåíèè ìîëåêóë ãàçà ðàâíîâåðîÿòíû, òî èç âñåõ ìîëåêóë, èìåþùèõ ñîñòàâëÿþùóþ ñêîðîñòè vx, òîëüêî ïîëîâèíà äâèæåòñÿ â ñòîðîíó ñòåíêè CD, âòîðàÿ ïîëîâèíà — â ñòîðîíó À (ò.å. â îáðàòíóþ). Ïîýòîìó , à ïîëíûé èìïóëüñ, ïåðåäàííûé ñòåíêå çà 1 ñ, ðàâåí 2m0vxZ = m0nvx2S. Ïîñêîëüêó èçìåíåíèå èìïóëüñà òî÷êè (òåëà) çà åäèíèöó âðåìåíè ðàâíî äåéñòâóþùåé íà íåãî ñèëå .  äåéñòâèòåëüíîñòè, ïîñêîëüêó ðå÷ü èäåò î áîëüøîì êîëè÷åñòâå ìîëåêóë, äâèæóùèõñÿ ñ ðàçíûìè ñêîðîñòÿìè, ñèëó ñëåäóåò óñðåäíèòü: .
Ñèëà ýòà çàâèñèò, òàêèì îáðàçîì, îò ñðåäíåãî êâàäðàòà ñêîðîñòè . Ïîñêîëüêó âñëåäñòâèå õàîòè÷íîñòè äâèæåíèÿ âñå íàïðàâëåíèÿ ðàâíîïðàâíû, òî:
Ñ äðóãîé ñòîðîíû, èçâåñòíî, ÷òî êâàäðàò ìîäóëÿ ëþáîãî âåêòîðà ðàâåí ñóììå êâàäðàòîâ åãî ïðîåêöèé íà îñè êîîðäèíàò, ïîýòîìó:
Óñðåäíÿÿ ýòî âûðàæåíèå ïî âñåì ìîëåêóëàì è ó÷èòûâàÿ , ïîëó÷èì:
Îòñþäà:
Ñ ó÷åòîì ïîñëåäíåé ôîðìóëû .
Ñëåäîâàòåëüíî, äàâëåíèå íà ñòåíêó ñîñóäà ðàâíî:
Ýòî îñíîâíîå óðàâíåíèå ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè. Ýòî óðàâíåíèå — ïåðâîå êîëè÷åñòâåííîå ñîîòíîøåíèå, ïîëó÷åííîå â ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè. Óðàâíåíèå ïîçâîëÿåò ïîëó÷èòü ñâÿçü ìåæäó äàâëåíèåì è ñðåäíåé êèíåòè÷åñêîé ýíåðãèåé ìîëåêóë .
.
Äàâëåíèå èäåàëüíîãî ãàçà ðàâíî äâóì òðåòÿì ñðåäíåé êèíåòè÷åñêîé ýíåðãèè ïîñòóïàòåëüíîãî äâèæåíèÿ ìîëåêóë, ñîäåðæàùèõñÿ â åäèíèöå îáúåìà.
Âàæíî ïîä÷åðêíóòü, ÷òî çäåñü ðå÷ü èäåò î ñðåäíåé êèíåòè÷åñêîé ýíåðãèè ìîëåêóë ãàçà. Ýòî îçíà÷àåò, ÷òî äàâëåíèå ãàçà — âåëè÷èíà, îðãàíè÷åñêè ñâÿçàííàÿ ñ òåì, ÷òî ãàç ñîñòîèò èç áîëüøîãî ÷èñëà ìîëåêóë. Íåò ñìûñëà ãîâîðèòü î äàâëåíèè, ñîçäàâàåìîì íåñêîëüêèìè ìîëåêóëàìè. Äàâëåíèå ãàçà – ïîíÿòèå, èìåþùåå ñòàòèñòè÷åñêèé õàðàêòåð (òàê íàçûâàþò ïîíÿòèÿ, èìåþùèå ñìûñë òîëüêî äëÿ ñèñòåì ñ î÷åíü áîëüøèì ÷èñëîì ÷àñòèö).
Êàëüêóëÿòîðû ïî ôèçèêå | |
| Ðåøåíèå çàäà÷ ïî ôèçèêå, ïîäãîòîâêà ê ÝÃÅ è ÃÈÀ, ìåõàíèêà òåðìîäèíàìèêà è äð. | |
| Êàëüêóëÿòîðû ïî ôèçèêå | |
Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ôèçèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ìîëåêóëÿðíîêèíåòè÷åñêàÿ òåîðèÿ ôîðìóëû | |
| Îñíîâû ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè, îñíîâíîå óðàâíåíèå ÌÊÒ èäåàëüíîãî ãàçà, ñðåäíåêâàäðàòè÷íàÿ ñêîðîñòü ìîëåêóë, ñðåäíÿÿ êèíåòè÷åñêàÿ ýíåðãèÿ ïîñòóïàòåëüíîãî äâèæåíèÿ ìîëåêóë è òä. | |
| Ìîëåêóëÿðíîêèíåòè÷åñêàÿ òåîðèÿ ôîðìóëû | |
Ìîëåêóëÿðíàÿ ôèçèêà | |
| Êèïåíèå, èñïàðåíèå, êîíäåíñàöèÿ, ïëàâëåíèå, êðèñòàëèçàöèÿ æèäêîñòè, âëàæíîñòü, àòîìíàÿ ìàññà, îñíîâû ìîëåêóëÿðíî-êèíåòè÷åñêîé òåîðèè | |
| Ìîëåêóëÿðíàÿ ôèçèêà | |
Источник
