Давление газа обусловлено столкновением молекул со стенками сосуда
Цели:
Обучающие: познакомить с понятием идеального
газа, вывести основное уравнение
молекулярно-кинетической теории газов.
Развивающие:
- развивать способности анализировать увиденное,
логическое мышление и творческое воображение
учащихся; - учить устанавливать причинно-следственные
связи в изучаемых явлениях, формулировать
эмпирические закономерности.
Воспитывающие: воспитывать ответственное
отношение к учебе, положительное отношение к
предмету физики.
Оборудование:
- воздушный насос, вакуумная тарелка, стеклянный
колокол, воздушный шарик - презентация (Приложение 1)
- карточки с тестом
Ход урока
I. Повторение пройденного. Беседа с учащимися с
использованием презентации (Приложение
1)
- Каковы основные положения
молекулярно-кинетической теории строения
вещества? (слайд 2) - Докажите, что все вещества состоят из молекул,
между которыми есть промежутки? (слайд 3) - В чем суть броуновского движения?
Доказательством каких положений является
броуновское движение? (слайд 4) - Что такое диффузия? Доказательством каких
положений является броуновское движение? (слайд
5) - Зависит ли скорость диффузии от температуры? (слайд
6) - О чем говорят опыты, показанные на слайде № 7
- Каковы размеры молекул? (слайд 8)
- Опишите словами модель взаимодействия между
молекулами или атомами твердого тела. (слайд 9) - В каком агрегатном состоянии находится
вещество, показанное на слайдах № 10,11,12? Укажите
особенности расположения и движения молекул в
различных агрегатных состояниях.
II. Изучение нового материала
Итак, мы знаем, что частицы в газах, в отличие от
жидкостей и твердых тел, располагаются друг
относительно друга на расстояниях, существенно
превышающих их собственные размеры. В этом
случае взаимодействие между молекулами
пренебрежимо мало и кинетическая энергия
молекул много больше энергии межмолекулярного
взаимодействия. Для выяснения наиболее общих
свойств, присущих всем газам, используют
упрощенную модель газа – идеальный газ.
Идеальный газ – это газ, у которого
взаимодействие между молекулами пренебрежимо
мало (слайд 13) (записываем в тетрадь)
Основные отличия идеального газа от реального
газа:
1. Частицы идеального газа – сферические тела
очень малых размеров, практически материальные
точки.
2. Между частицами отсутствуют силы
межмолекулярного взаимодействия.
3. Соударения частиц являются абсолютно упругими.
Реальные разреженные газы действительно ведут
себя подобно идеальному газу. Воспользуемся
моделью идеального газа для объяснения
происхождения давления газа.
Вспомним опыт из 7 класса (слайд 14)
Почему при откачивании воздуха из-под колокола
воздушный шарик раздувается?
(Это значит, что газ внутри шарика оказывает
давление, и когда внешнее давление при
откачивании уменьшается, шар благодаря
внутреннему давлению воздуха начинает
раздуваться?
Что же такое давление газа? (слайд 15)
(Давление газа – это результат ударов молекул
газа о стенки сосуда)
Сегодня мы с вами попытаемся ответить, от чего
зависит давление газа? (Слайд 16)
Даю возможность учащимся сделать
предположения, от чего может зависеть давление
газа.
Выведем основное уравнение
молекулярно-кинетической теории газов (слайд
17)
Пусть в некотором объеме есть молекулы, масса
каждой mo, их число равно N, и
движутся они со скоростью v (очевидно, что
скорости у всех молекул различны, однако среднее
значение модуля скорости v вполне определенное).
Учитель делает рисунок на доске, учащиеся в
тетрадях
При каждом ударе молекулы действуют на стенку
сосуда с некоторой силой. Складываясь друг с
другом, силы ударов отдельных частиц образуют
некоторую силу давления, постоянно действующую
на стенку, а значит и давление.
От чего же зависит давление газа?
Во-первых, от массы: чем больше масса
молекулы, тем сильнее удар, значит здесь прямая
пропорциональная зависимость давления от массы
Запишем:
1) р mo
Во-вторых, от скорости: чем быстрее движутся
молекулы, тем сильнее будут удары, а значит и
давление.
Запишем:
2) р v
В-третьих, есть еще одна зависимость от
скорости: чем быстрее движутся молекулы, тем чаще
удары, а значит и давление.
Запишем:
3) р v
В-четвертых, давление газа зависит от числа
молекул в данном сосуде, а точнее от концентрации
n.
Концентрация – физическая величина, равная
числу молекул, содержащихся в единице объема (n =
N/V)
(определение концентрации и единицы
измерения записываем в тетрадь)
Запишем:
4) р n
В результате получаем: давление газа прямо
пропорционально концентрации частиц, массе
частицы и квадрату скорости частицы
Это и есть основное уравнение
молекулярно-кинетической теории идеального
газа. В этом уравнении коэффициент 1/3 означает,
что в трехмерном пространстве только треть
молекул участвует в движении в определенном
направлении (по оси х, например).
Мы получили основное уравнение МКТ идеального
газа из общих соображений, но его можно строго
вывести, опираясь на законы классической
механики (§ 63 , Мякишев Г.Я.)
Это уравнение можно записать по-другому, если
умножить и разделить правую часть уравнения на 2.
P = 2/3· n·Ек, где Ек = mo·v2 /2
Давление идеального газа пропорционально
произведению концентрации молекул и средней
кинетической энергии поступательного движения
молекул
III. Закрепление изученного материала.
Выполнение тестов учащимися.
Цель заданий: определить степень усвоения
нового материала
1. Давление газа на стенку сосуда обусловлено
а) притяжением молекул друг к другу
б) столкновениями молекул со стенками сосудов
в) столкновением молекул газа между собой
г) проникновением молекул сквозь стенки сосуда
2. Как изменилось давление идеального газа, если
в данном объеме скорость каждой молекулы газа
увеличилась в 2 раза, а концентрация молекул
осталась без изменения?
а) увеличилось в 2 раза
б) увеличилось в 4 раза
в) уменьшилось в 2 раза
г) уменьшилось в 4 раза
3. При повышении температуры идеального газа в
запаянном сосуде его давление увеличивается. Это
объясняется тем, что с ростом температуры…
а) увеличиваются размеры молекул газа
б) увеличивается энергия движения молекул газа
в) увеличивается потенциальная энергия молекул
газа
г) увеличивается хаотичность движения молекул
газа
4. Как изменится концентрация молекул газа при
уменьшении объема сосуда в 2 раза?
а) увеличится в 2 раза
б) уменьшится в 2 раза
в) не изменится
г) уменьшится в 4 раза
5. При уменьшении температуры средняя
кинетическая энергия молекул
а) увеличится
б) уменьшится
в) не изменится
г) иногда увеличится, иногда уменьшится
6. Какое утверждение неправильно?
При неизменных условиях
а) давление газа постоянно
б) скорости всех молекул одинаковы
в) внутренняя энергия газа постоянна
г) температура газа постоянна
7. В сосуде водород. Как изменится давление газа,
если водород заменить кислородом так, что
количество молекул и температура останутся
неизменными?
а) увеличится в 4 раза
б) уменьшится в 16 раз
в) не изменится
г) увеличится в 16 раз
IV. Проверка выполненных тестов
Правильные ответы: 1 – Б, 2 – Б, 3 – Б, 4 – А, 5 – Б, 6
– Б , 7 – Г
V. Решение задачи
В ампуле содержится водород (Н2).
Определите давление газа, если его концентрация
равна 2•1022 м -3, а средняя
квадратичнаяскорость движения молекул
водорода 500 м/с.
VI. Задание на дом.
§ 61, § 63, Физика 10 класс Г.Я. Мякишев, Б.Б Буховцев,
записи в тетради, упр. 11 (задачи 8,9)
VII. Подведение итогов урока.
Литература:
- Физика. 10 класс: учебник для
общеобразовательных учреждений: базовый и
профильный уровни /Г.Я Мякишев, Б.Б.Буховцев, Н.Н.
Сотский; – М.: Просвещение, 2009. - Физика. Тесты. 10-11 классы: учебно-методическое
пособие / Н.К. Гладышева, И.И. Нурминский, А.И.
Нурминский и др. – М.: Дрофа, 2005.
Источник
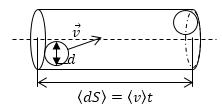
В газе молекулы свободно движутся. Сталкиваются периодически между собой. Между двумя последовательными соударениями молекула движется равномерно и прямолинейно. Определим среднее количество столкновений молекулы газа с другими молекулами на время t=1с. Обозначим через $leftlangle dSrightrangle $ элементарный средний путь, пройденный молекулой, считаем, что молекула двигалась прямолинейно со средней скоростью $leftlangle overrightarrow{v}rightrangle $. Будем считать, что газ идеальный, то есть его молекулы представляют собой твердые сферы диаметром d (это так называемый эффективный диаметр молекулы). Тогда число столкновений (z) молекулы с другими за t=1с будет равно количеству молекул, центры которых находятся в цилиндре (рис. 1), высота цилиндра $leftlangle overrightarrow{v}rightrangle t$, и диаметром d:

Рис. 1
Скорость – вектор, используем относительную среднюю скорость, зная, что
подставим в (1) вместо $leftlangle vrightrangle :$
Расстояние, которое проходит молекула между двумя последовательными столкновениями, называется длинной свободного пробега ($lambda $):
где $sigma$- эффективное поперечное сечение соударения. Из выражения (4) видно, что средняя длина свободного пробега молекулы не зависит о температуры. Длина свободного пробега молекулы весьма важная физическая величина в МКТ. Используя ее, рассчитываются коэффициенты переноса.
Давление газа на стенки сосуда
Молекулы газа сталкиваются не только друг с другом, но и со стенками сосуда, в котором находится газ. Движущиеся молекулы газа обладают импульсом, сталкиваясь со стенками сосуда, молекулы передают свой импульс препятствию. Этим и обусловлено давление газа на стенки сосуда. Если мы рассматриваем идеальный газ, то считаем соударения молекул абсолютно упругими. Пусть газ находится в состоянии равновесия. Определим связь между давлением газа и скоростью отдельных его молекул. Известно, что $p={frac{triangle F_n}{triangle S} , }$ давление газа есть сила, действующая на единичную площадку поверхности сосуда. Сила, есть импульс, которые передают молекулы в единицу времени стенке сосуда ($triangle overrightarrow{F}=frac{triangle overrightarrow{p}}{triangle t}$). Найдем импульс. Молекула, ударяясь о стеку сосуда, отскакивает от нее, причем угол падения равен углу отражения (рис.2). Тогда стенке передается только $p_x,$ и $triangle p_x=mv_x-(-mv_x)$=2$ mv_x$
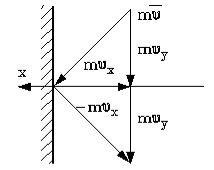
Рис. 2
Количество молекул, которые ударяются о единичную площадку стенки сосуда с газом, определяется по формуле:
Импульс, который получает стенка в этом случае, равен:
[triangle p_x=zcdot 2 mv_x=2 m{v_x}^2cdot n_0cdot tleft(6right),]
$n_0$ — количество молекул, которые обладают скоростью $v_x$ и находятся в единице объема газа.
Полный импульс
При этом полный импульс, который получает стенка, равен сумме:
[triangle p=sumlimits_{v_x>0}{2 m{v_x}^2cdot n_0cdot triangle t} left(7right).]
Умножим и разделим (7) на $frac{n}{2}$, здесь n — концентрация молекул в газе:
[triangle p=sumlimits_{v_x>0}{frac{2 m{v_x}^2cdot n_0cdot triangle t}{frac{n}{2}}}cdot frac{n}{2}left(8right).]
[sumlimits_{v_x>0}{frac{{v_x}^2cdot n_0cdot }{frac{n}{2}}}=leftlangle {v_x}^2rightrangle to triangle p=frac{mleftlangle {v_x}^2rightrangle triangle tn}{2}to F=frac{triangle p}{triangle t}=frac{mleftlangle {v_x}^2rightrangle n}{2}to p=frac{mleftlangle {v_x}^2rightrangle n}{2}left(9right).]
Напомню, что мы рассматривали единичную площадку.
Считая, что газ изотропен, имеем:
[leftlangle v^2rightrangle =leftlangle {v_x}^2rightrangle +leftlangle {v_y}^2rightrangle +leftlangle {v_z}^2rightrangle =3leftlangle {v_x}^2rightrangle left(10right)]
Следовательно, связь между давлением, скоростью отдельной молекулы и ее массы имеет вид:
[p=frac{2mleftlangle v^2rightrangle n}{3cdot 2}=frac{2}{3}nleftlangle E_krightrangle left(11right).]
Уравнение (11) доказывает, что давление газа — следствие действия отдельных молекул, и оно пропорционально средней кинетической энергии поступательного движения молекул.
Пример 1
Задание: При атмосферном давлении и температуре $t=0^oС$ длина свободного пробега молекулы водорода равна 0,1 мк.м. Оцените диаметр этой молекулы.
Решение:
Диаметр молекулы можно оценить, зная длину свободного пробега молекулы, так как:
[lambda =frac{1}{sqrt{2}pi d^2cdot n} left(1.1right)]
Концентрацию молекул водорода можно найти из условий задачи, используя уравнение состояния идеального газа (водород при атмосферном давлении и заданной температуре можно считать идеальным газам):
[p=nkTto n=frac{p}{kT}left(1.2right).]
Подставим (1.2) в (1.1), получим:
[lambda =frac{kT}{sqrt{2}pi d^2cdot p}to d=sqrt{frac{kT}{lambda psqrt{2}pi }}left(1.3right)]
Проведем расчёты, зная, что атмосферное давление это $papprox 10^5Па, lambda =0,1 мк.м=10^{-7}м, t=0^0Сto T=273K $:
[d=sqrt{frac{1,38cdot 10^{-23}273}{sqrt{2}cdot 3,14cdot 10^5cdot 10^{-7}}}=sqrt{8,5cdot 10^{-20}}=2,3cdot 10^{-10}(м)]
Ответ: Диаметр молекулы водорода порядка $2,3cdot 10^{-10}м.$
Задание: Можно ли вычислить среднюю квадратичную скорость молекулы по заданным: средней энергии поступательного движения молекул$- leftlangle E_krightrangle $и молярной массе газа $mu sigma$
Решение:
В качестве основы для решения используем уравнение:
[p=frac{mleftlangle v^2rightrangle n}{3}=frac{2}{3}nleftlangle E_krightrangle to leftlangle v^2rightrangle =frac{2leftlangle E_krightrangle }{m}left(2.1right),]
здесь $m$- масса одной молекулы, а мы знаем, что:
[frac{m}{mu }=frac{1}{N_A}to m=frac{mu }{N_A}to leftlangle v^2rightrangle =frac{2leftlangle E_krightrangle N_A}{mu }.]
$N_A$- число Авогадро, величина известная.
Ответ: По заданным параметрам среднеквадратичную скорость вычислить можно, используя формулу: $leftlangle v_{kv}rightrangle =sqrt{frac{2leftlangle E_krightrangle N_A}{mu }}$.
Источник
