Давление газа в сосуде где концентрация молекул составляет
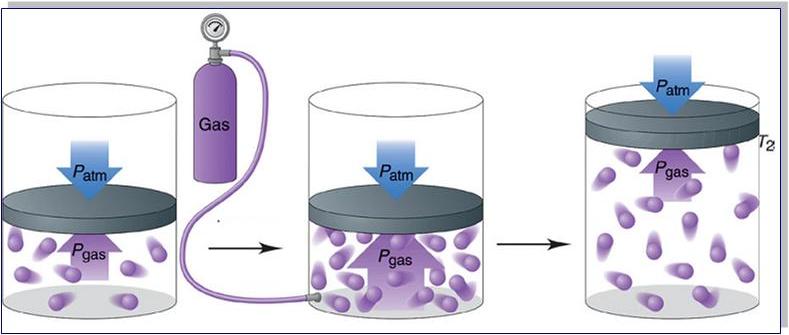
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах

Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
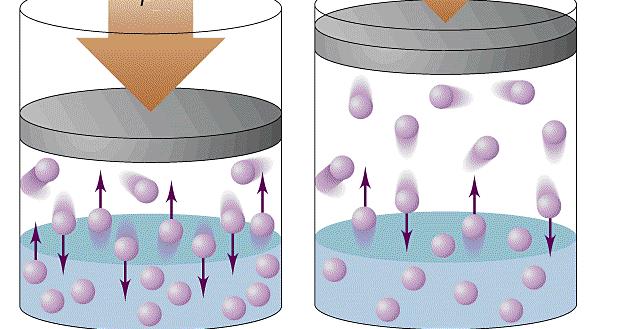
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
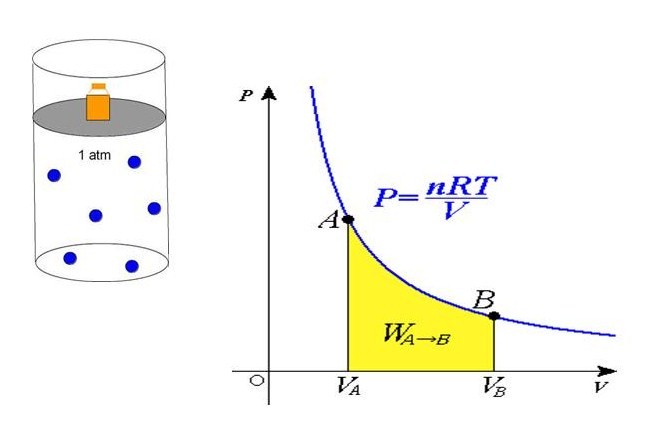
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
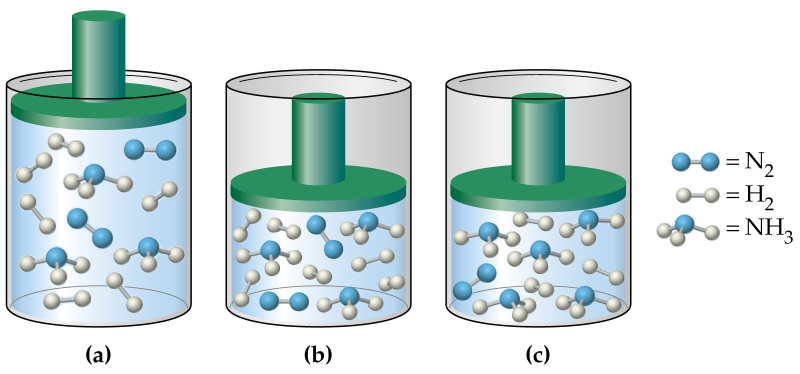
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
5.4. Практическое применение уравнения состояния идеального газа
5.4.2. Уравнение состояния для газа в закрытом сосуде
При рассмотрении идеального газа, находящегося в закрытом сосуде (баллоне), необходимо учитывать, что изменение термодинамических параметров происходит при постоянной массе газа.
Для идеального газа, находящегося в закрытом сосуде, необходимо учитывать следующее:
- масса газа, находящегося в закрытом сосуде, вследствие изменения его термодинамических параметров не изменяется:
m = const;
- объем газа, заполняющего сосуд определенного объема, также фиксирован: V = const;
- постоянными также остаются следующие параметры газа:
ρ = const; ν = const; n = const;
где ρ — плотность газа; ν — количество вещества (газа); n — концентрация молекул (атомов) газа.
Для идеального газа, находящегося в закрытом сосуде и изменяющего свое состояние, уравнение Менделеева — Клапейрона записывается в виде системы (рис. 5.8):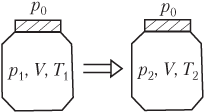
p1V=νRT1,p2V=νRT2,}
где p
1, T
1 — давление и температура газа в начальном состоянии; p
2, T
2 — давление и температура газа в конечном состоянии; V — объем баллона; ν — количество газа; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К).
Термин избыточное давление, встречающийся в задачах об идеальном газе в закрытом сосуде (баллоне), означает абсолютную разность между давлением газа, находящегося в сосуде, и давлением на стенки сосуда снаружи:
p
изб = |p − p
0|,
где p — давление газа, находящегося внутри сосуда; p
0 — давление (атмосферное либо гидростатическое) на стенки сосуда снаружи.
Пример 13. Баллон рассчитан на максимальное избыточное давление 150 МПа. В него накачали газ при температуре 300 К до давления 120 МПа. Постепенно нагревая газ, баллон погружают в воду плотностью 1000 кг/м3 на глубину 1000 м. До какой максимальной температуры можно нагреть газ в баллоне, чтобы он не взорвался?
Решение. Запишем уравнение Менделеева — Клапейрона для двух состояний газа, находящегося в баллоне:
- в начале нагревания
p
1V = νRT
1;
- в конце нагревания
p
2V = νRT
2;
где p
1 — первоначальное давление газа в баллоне; p
2 — давление газа в баллоне в конце нагревания; V — объем газа (баллона), V = const; ν — количество вещества (газа) в баллоне; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура газа в начале процесса; T
2 — температура газа в конце процесса.
Отношение уравнений
p1Vp2V=νRT1νRT2
позволяет определить давление газа в конце процесса:
p2=p1T2T1.
В условии задачи задано максимальное избыточное давление, определяемое формулой
pизбmax=|p2−p0|,
где p
0 — давление снаружи баллона; p
2 — давление газа внутри баллона.
При погружении баллона в воду с одновременным нагреванием указанные давления снаружи и внутри баллона определяются следующими формулами:
- снаружи (сумма атмосферного и гидростатического давлений) —
p
0 = p
атм + p
гидр = p
атм + ρ0gh,
где p
атм — атмосферное давление; p
гидр — гидростатическое давление, p
гидр = ρ0gh; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — глубина погружения баллона;
- внутри (давление газа) —
p2=p1T2T1,
где T
2 — максимальная температура газа (искомая величина).
Подстановка выражений для давлений внутри и снаружи баллона в формулу для избыточного давления дает
pизбmax=|p1T2T1−ρ0gh−pатм|≈|p1T2T1−ρ0gh|,
так как p
атм << ρ0gh, p
атм << p
2.
Данное уравнение содержит модуль разности, что приводит к двум независимым уравнениям:
pизбmax=p1T2T1−ρ0gh, pизбmax=ρ0gh−p1T2T1,
из которых следуют две формулы для расчета искомой величины:
T2=T1⋅ρ0gh+pизбmaxp1, T2=T1⋅ρ0gh−pизбmaxp1.
Максимальному значению искомой температуры соответствует значение, рассчитанное по первой формуле:
T2=300⋅1000⋅10⋅1000+150⋅106120⋅106=400 К.
Чтобы баллон не взорвался, его можно погрузить на заданную глубину, одновременно нагревая до температуры 400 К.
Пример 14. Бутылка емкостью 0,75 л выдерживает максимальное избыточное давление 150 кПа. Из бутылки откачивают воздух и запечатывают некоторое количество твердого углекислого газа с молярной массой 44,0 г/моль. Атмосферное давление равно 100 кПа. Считая, что объем твердого углекислого газа пренебрежимо мал по сравнению с объемом бутылки, найти его максимальную массу, которая не вызовет взрыва бутылки при температуре 300 К?
Решение. Запишем уравнение Менделеева — Клапейрона для углекислого газа, находящегося в бутылке, после его превращения в газообразное состояние:
pV=mMRT,
где p — давление углекислого газа в бутылке; V — объем газа (бутылки); m — масса углекислого газа в бутылке; M — молярная масса углекислого газа; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа.
Записанное уравнение позволяет получить выражение для расчета давления газа внутри бутылки:
p=mRTVM.
В условии задачи задано максимальное избыточное давление, определяемое формулой
pизбmax=|p−p0|,
где p
0 — давление снаружи бутылки.
Указанные давления снаружи и внутри бутылки определяются следующим образом:
- снаружи (атмосферное давление) — p
0; - внутри (давление углекислого газа) —
p=mRTVM,
где m соответствует искомой величине — максимальной массе углекислого газа.
Подстановка выражений для давлений внутри и снаружи баллона в формулу для избыточного давления дает
pизбmax=|mRTVM−p0|.
Данное уравнение содержит модуль разности, что приводит к двум независимым уравнениям:
pизбmax=mRTVM−p0, pизбmax=p0−mRTVM,
из которых следуют две формулы для расчета искомой величины:
m=VM(p0+pизбmax)RT, m=VM(p0−pизбmax)RT.
Максимальному значению искомой массы соответствует значение, рассчитанное по первой формуле:
m=0,75⋅10−3⋅44,0⋅10−3(100+150)⋅1038,31⋅300=3,3⋅10−3 кг=3,3 г.
Чтобы бутылка не взорвалась, в нее можно запечатать не более 3,3 г твердого углекислого газа.
Пример 15. В наличии имеется неограниченное количество баллонов объемом по 4,0 л, заполненных некоторым идеальным газом до давления 500 кПа. Баллоны предназначены для наполнения газом оболочки аэрозонда и их можно соединять между собой. Сколько баллонов с газом необходимо одновременно подсоединить к пустой оболочке аэрозонда объемом 800 дм3, чтобы наполнить ее до давления 100 кПа, равного атмосферному? Температура газа при заполнении оболочки не изменяется.
Решение. Для осуществления процесса, описанного в условии задачи, требуется определенное количество газа ν.
Необходимое количество газа заполняет следующий объем:
- в начале процесса (до заполнения оболочки)
V
1 = NV
бал,
где N — количество баллонов; V
бал — объем одного баллона, V
бал = 4,0 л;
- в конце процесса (после заполнения оболочки)
V
2 = NV
бал + V
обол,
где V
обол — объем оболочки, V
обол = 800 дм3.
Указанное количество газа находится при давлении:
- в начале процесса (до заполнения оболочки) —
p
1 = 500 кПа
и совпадает с давлением газа в каждом из баллонов;
- в конце процесса (после заполнения оболочки) —
p
2 = 100 кПа
и совпадает с давлением в оболочке.
Считая процесс заполнения газом оболочки аэрозонда изотермическим, запишем уравнение Менделеева — Клапейрона следующим образом:
- в начале процесса (до заполнения оболочки) —
p
1V
1 = νRT,
где ν — количество вещества (газа) в оболочке; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- в конце процесса (после заполнения оболочки) —
p
2V
2 = νRT.
Равенство
p
1V
1 = p
2V
2,
записанное в явном виде
p
1NV
бал = p
2(NV
бал + V
обол),
позволяет получить формулу для вычисления искомого числа баллонов:
N=VоболVбал⋅p2p1−p2.
Произведем расчет:
N=800⋅10−34,0⋅10−3⋅100⋅103(500−100)⋅103=50.
Следовательно, для заполнения оболочки до указанного давления необходимо 50 баллонов с газом.
Пример 16. Аэростат, оболочка которого заполнена азотом с молярной массой 28 г/моль, находится в воздухе. Молярная масса воздуха равна 29 г/моль. Массы гондолы и оболочки аэростата пренебрежимо малы. Во сколько раз возрастет подъемная сила аэростата, если азот в его оболочке заменить на водород с молярной массой 2,0 г/моль, не изменяя при этом объем аэростата?
Решение. Силы (сила тяжести mg→ и сила Архимеда F→A), действующие на аэростат, показаны на рисунке.
Подъемная сила — это векторная сумма силы тяжести и силы Архимеда:
F→под=F→A+mg→,
где F→A — сила Архимеда, действующая на оболочку со стороны воздуха; mg→ — сила тяжести; m — масса газа, заполняющего оболочку аэростата; g→ — ускорение свободного падения.
В проекциях на вертикальную ось подъемная сила определяется следующими выражениями:
- при заполнении оболочки азотом —
F
под1 = F
A1 − m
1g,
где F
A1 — модуль силы Архимеда, действующей на оболочку аэростата при заполнении оболочки азотом, F
A1 = ρ0gV
1; ρ0 — плотность воздуха; V
1 — объем оболочки аэростата при заполнении ее азотом (объем воздуха, вытесненного оболочкой); m
1 — масса азота, заполняющего оболочку, m
1 = ρ1V
1; ρ1 — плотность азота;
- при заполнении оболочки водородом —
F
под2 = F
A2 − m
2g,
где F
A2 — модуль силы Архимеда, действующей на оболочку аэростата при заполнении оболочки водородом, F
A2 = ρ0gV
2; V
2 — объем оболочки аэростата при заполнении ее водородом (объем воздуха, вытесненного оболочкой); m
2 — масса водорода, заполняющего оболочку, m
2 = ρ2V
2; ρ2 — плотность водорода.
Искомой величиной является отношение
Fпод2Fпод1=FA2−m2gFA1−m1g.
С учетом записанных выражений для сил Архимеда, масс азота и водорода, а также равенства объемов оболочки при заполнении ее азотом и водородом (V
1 = V
2), указанное отношение принимает вид
Fпод2Fпод1=ρ0gV2−ρ2V2gρ0gV1−ρ1V1g=(ρ0−ρ2)V2g(ρ0−ρ1)V1g=ρ0−ρ2ρ0−ρ1.
Плотности воздуха, азота и водорода определим как отношения:
- для воздуха
ρ0=M0Vμ0,
где M
0 — молярная масса воздуха; V
µ0 — молярный объем воздуха;
- для азота
ρ1=M1Vμ1,
где M
1 — молярная масса азота; V
µ1 — молярный объем азота;
- для водорода
ρ2=M2Vμ2,
где M
2 — молярная масса водорода; V
µ2 — молярный объем водорода.
Молярные объемы (объемы одного моля) воздуха, азота и водорода равны между собой, так как газы находятся при одних и тех же условиях:
V
µ0 = V
µ1 = V
µ2 = V
µ.
Поэтому формула для расчета искомого отношения приобретает вид
Fпод2Fпод1=ρ0−ρ2ρ0−ρ1=M0−M2M0−M1.
Расчет дает значение:
Fпод2Fпод1=29⋅10−3−2,0⋅10−329⋅10−3−28⋅10−3=27.
При замене азота на водород в оболочке аэростата его подъемная сила возрастет в 27 раз.
Пример 17. Воздушный шар с температурой 300 К находится в воздухе при атмосферном давлении 100 кПа. Молярная масса воздуха составляет 29,0 г/моль. Объем воздушного шара равен 830 дм3, а масса его оболочки равна 333 г. На сколько градусов необходимо нагреть газ в оболочке, чтобы шар взлетел? Воздух в оболочке шара сообщается с атмосферой.
Решение. Силы, действующие на воздушный шар, показаны на рисунке:
- сила Архимеда
F
A = ρ0gV,
где ρ0 — плотность воздуха, окружающего шар; g — модуль ускорения свободного падения; V — объем оболочки шара (объем вытесненного оболочкой воздуха);
- сила тяжести
mg = (m
обол + m
возд)g,
где m
обол — масса оболочки; m
возд — масса воздуха в оболочке, m
возд = ρV; ρ — плотность воздуха внутри оболочки.
Шар взлетает, когда выполняется равенство
F→A+mg→=0,
или, в проекции на вертикальную ось, —
F
A − mg = 0.
Преобразуем равенство (условие равновесия шара в воздухе)
F
A = mg
с учетом записанных выше выражений
ρ0gV = (m
обол + m
возд)g, или (ρ0 − ρ)V = m
обол.
Входящие в равенство плотности воздуха не известны, но фигурируют в качестве параметра в уравнении состояния:
- для воздуха снаружи оболочки воздушного шара
p0=ρ0RT1M,
где p
0 — атмосферное давление; ρ0 — плотность воздуха снаружи оболочки; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T
1 — температура окружающего шар воздуха; M — молярная масса воздуха;
- для воздуха внутри оболочки воздушного шара
p=ρRT2M,
где p — давление воздуха внутри оболочки; ρ — плотность воздуха внутри оболочки; T
2 — температура воздуха внутри оболочки.
Давления воздуха внутри и снаружи оболочки воздушного шара одинаковы, так как воздух, находящийся в оболочке, сообщается с атмосферой; поэтому
p = p
0.
Плотности:
- для воздуха снаружи оболочки воздушного шара
ρ0=p0MRT1;
- для воздуха внутри оболочки воздушного шара
ρ=p0MRT2.
Подставим выражения для плотностей в условие равновесия шара в воздухе:
(1T1−1T2)p0MVR=mобол.
Температура воздуха внутри оболочки, при которой шар начинает взлетать, определяется как
T2=p0MVT1p0MV−RT1mобол,
а искомая разность —
ΔT=T2−T1=p0MVT1p0MV−RT1mобол−T1=T1p0MVRT1mобол−1.
Произведем вычисление:
ΔT=300100⋅103⋅29,0⋅10−3⋅830⋅10−38,31⋅300⋅333⋅10−3−1=158 К.
Следовательно, чтобы воздушный шар начал взлетать, воздух в его оболочке необходимо нагреть на 158 К, или 158 °С.
Пример 18. Камеру футбольного мяча объемом 3,00 л накачивают с помощью насоса, забирающего из атмосферы 0,150 л воздуха при каждом качании. Атмосферное давление составляет 100 кПа. Определить давление в камере после 30 качаний, если первоначально она была пустой. Температура постоянна.
Решение. За N качаний насос забирает из атмосферы определенное количество воздуха ν. Это же количество воздуха попадает в камеру футбольного мяча.
Указанное количество воздуха имеет следующий объем:
- воздух, забранный из атмосферы за N качаний насоса, —
V
1 = NV
нас,
где V
нас — объем насоса, V
нас = 0,150 л; N — количество качаний;
- воздух, накачанный в камеру футбольного мяча, —
V
2 = V
мяч,
где V
мяч — объем камеры мяча, V
мяч = 3,00 л.
Данное количество воздуха находится при следующем давлении:
- воздух, забранный из атмосферы за N качаний насоса, —
p
1 = 100 кПа
совпадает с атмосферным давлением;
- воздух, накачанный в камеру футбольного мяча, — p
2 (является искомой величиной).
Считая процесс заполнения воздухом камеры мяча изотермическим, запишем уравнение Менделеева — Клапейрона следующим образом:
- для воздуха, забранного из атмосферы за N качаний насоса, —
p
1V
1 = νRT,
где R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К); T — температура газа (не изменяется в ходе процесса);
- для воздуха, накачанного в камеру футбольного мяча, —
p
2V
2 = νRT.
Равенство
p
1V
1 = p
2V
2,
записанное в явном виде
p
1NV
нас = p
2V
мяч,
позволяет получить формулу для вычисления давления в камере футбольного мяча:
p2=p1NVнасVмяч.
Произведем вычисление:
p2=100⋅103⋅30⋅0,15⋅10−33,00⋅10−3=150⋅103 Па=150 кПа.
Источник


