Давление газа в сосуде термодинамика
Определение 1
Термодинамика – раздел науки, который исследует тепловые процессы, происходящие в физических телах, не связывая их напрямую с молекулярным строением вещества.
Рисунок 1. Параметры состояния в термодинамике. Автор24 — интернет-биржа студенческих работ
В термодинамике полагается, что все явления тепла в телах характеризуются только макроскопическими параметрами:
- давлением;
- объемом;
- температурой.
Эти показатели невозможно применить к отдельно взятым атомам или молекулам, то, в отличие от молекулярно-кинетической гипотезы, в указанном научном направлении молекулярное строение элементов в тепловых процессах не учитывается.
Давление в термодинамике представляет собой термодинамический параметр $P$, который определяет элементарную работу, совершаемую определенной системой при медленном изменении её объёма $V$, вызываемом хаотичным перемещением внешних тел. При деформации упругих веществ сила, влияющая на единицу поверхности, не перпендикулярна к ней.
Замечание 1
Вместо давления в этом случае вводят тензор максимальных напряжений. Элементарная работа равна величине тензору деформаций.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
При равномерном и всестороннем сжатии тела только нормальные напряжения будут отличны от нуля, которые равны начальному давлению. В статистической физике давление определяется как производная от средней энергии $E$ по объёму при действии постоянной энтропии $S$, или как производная от свободной внутренней энергии $F$ по объему при постоянной температуре T. То есть зависимость $P$ от $T$ и $V$ определяется уравнением состояния. В равновесном и стабильном состоянии иногда возможны метастабильные состояния с $P$
Изменение внутреннего давления механической работой
Рисунок 2. Применение поршня в цилиндре. Автор24 — интернет-биржа студенческих работ
Внутреннее давление материального тела можно изменить, совершив над ним определенную механическую работу. Если работа совершается над веществом, то давление автоматически превращается во внутреннюю энергию. А если работу совершает само тело, то его внутреннее давление становится механическим.
Почти до конца XIX столетия ученые считали, что в природе существует невесомое вещество – теплород, которое передает тепло от одного тела к другому. Чем больше теплорода втекает в вещество, тем теплее оно будет, и наоборот.
Однако в конце 1798 года учёный граф Бенджамин Румфорд решил опровергнуть данную теорию. Причиной тому были нестабильные нагревания стволов пушек при сверлении. Исследователь предположил, что результатом нагревания и изменения давления является механическая работа, которая наблюдается в ходе трения сверла о ствол.
Румфорд провел научный эксперимент. Чтобы увеличить силу трение и внутреннее давление, он взял тупое сверло, а сам ствол разместил в бочку с холодной водой. К концу третьего часа сверления вода в бочке начала закипать. Это доказало, что ствол получил тепло и изменил собственное давление при совершении механической работы над ним.
Критическое давление в термодинамике
Рисунок 3. Изменение внутренней энергии в термодинамике. Автор24 — интернет-биржа студенческих работ
В термодинамических стабильных процессах, когда линия объекта пересекает или кривую парообразования, или же кривую сублимации, газообразная фаза выступает в качестве пара.
Определение 2
Критическое давление – это вид давления, выше которого происходит расслоение вещества на две равновесно и одновременно сосуществующие фазы: газ и жидкость невозможны при любой температуре.
Это определение считается классически, и оно вполне применимо к термодинамическим процессам в простых концепциях. При более сложных системах критическое давление представляет собой нижнюю по давлению границу области физических явлений, в которых невозможно возникновение двухфазного состояния вещества «газ – жидкость» ни при каких изменениях давления и напряженности.
Эта формулировка критического давления иллюстрируется чаще всего в физике, когда необходимо изучить область, охватывающую не только часть газообразной фазы, но и элементы жидкой фазы, расположенные ниже изотермы.
Замечание 2
Для сверхкритической сферы за условную границу «жидкость-газ» принято подсоединять критическую изотерму.
Если давление такого перехода значительно больше давления в критической точке, то материальное вещество из твердого (кристаллического) состояния трансформируется в газообразное состояние, минуя на пути жидкое состояние.
Из фазовых диаграмм, которые чаще всего используются в термодинамике, аномального вещества не видно, так как на них не показана та часть системы, где имеющее при больших давлениях кристаллические модификации вещества снова приобретает нормальные свойства.
На фазовой диаграмме нормального элемента этот переход из твердого состояние сразу в газообразное показан в виде изотропного процесса.
Объединение свободно и активно движущихся молекул в каплю жидкости при очередном сжижении газа происходит исключительно под воздействием сил взаимного притяжения. При таком процессе кинетическая энергия относительного движения частиц больше энергии притяжения молекул, поэтому появление капель жидкости (сосуществование двух фаз) на практике невозможно.
Опыты Эндрюса
Ученый установил, что если сжимать газ при постоянной температуре и давлении, то напряженность вещества будет уменьшаться, однако с определенного показателя она остается постоянной, но в сосуде начинает появляться жидкость. По мере сжатия давления количество увеличивается, в результате чего все элементы превращаются в жидкость.
Определение 3
Постоянное давление в термодинамике называют давлением насыщенного пара.
Эндрюс экспериментальным путем доказал, что если воздействовать на газ более высокими температурами, то кривая зависимости начального давления от объема пойдет выше, соответственно, возрастет давление насыщенного пара, а поток вещества в жидком состоянии уменьшится. Таким образом, длина горизонтального участка изотермы с повышением температуры опустится до нуля.
Исследователь также обнаружил, что существует температура, при которой любая материальная точка стягивается к газу, при этом объемы вещества в жидком состоянии становятся одинаковыми, то есть практически полностью исчезает различие между газом и жидкостью. Такая температура в термодинамике называется критической.
При температуре выше критической, давление настолько сильно, что элементы могут существовать только в газообразном состоянии при тепловом движении и высокой плотности. В принципе возможно сжать газ до более низких показателей, чем у жидкостей, но при таком снятии молекулы вещества внезапно разлетаются, занимая собой весь предоставленный объем. Отсюда ясно, почему до работ Эндрюса физики не могли получить в жидком состоянии такие элементы, как азот, водород и кислород, даже сжимая их до крайне высоких давлений – просто у таких веществ очень низкое критическое давление и температура, и для их сжижения необходимо охлаждение.
Источник
Рассмотрим подробнее, что представляет собой один из основных параметров состояния – давление P. Ещё в XVIII веке Даниил Бернулли предположил, что давление газа есть следствие столкновения газовых молекул со стенками сосуда. Именно давление чаще всего является единственным сигналом присутствия газа.
Итак, находящиеся под давлением газ или жидкость действуют с некоторой силой на любую поверхность, ограничивающую их объем. В этом случае сила действует по нормали к ограничивающей объем поверхности. Давление на поверхность равно:
| , |
где ΔF – сила, действующая на поверхность площадью ΔS.
Можно также говорить о давлении внутри газа или жидкости. Его можно измерить, помещая в газ или жидкость небольшой куб с тонкими стенками, наполненный той же средой (рис. 1.1).

Рис. 1.1
Поскольку среда покоится, на каждую грань куба со стороны среды действует одна и та же сила ΔF. В окрестности куба давление равно ΔF/ΔS, где ΔS – площадь грани куба. Из этого следует, что внутреннее давление является одним и тем же во всех направлениях и во всем объеме независимо от формы сосуда. Этот результат называется законом Паскаля: если к некоторой части поверхности, ограничивающей газ или жидкость, приложено давление P0, то оно одинаково передается любой части этой поверхности.
Допустим, автомобиль поднимается гидравлическим домкратом, состоящим, как показано на рисунке 1.2, из двух соединенных трубкой цилиндров с поршнями. Диаметр большого цилиндра равен 1 м, а диаметр малого – 10 см. Автомобиль имеет вес F2. Найдем силу давления на поршень малого цилиндра, необходимую для подъема автомобиля.
Рис. 1.2
Поскольку оба поршня являются стенками одного и того же сосуда, то в соответствии с законом Паскаля они испытывают одинаковое давление. Пусть – давление на малый поршень, а – давление на большой поршень. Тогда, т.к. P1 = P2, имеем:
| , |
Отсюда F1=F2(S1/S2)=0,01F2
Таким образом, для подъема автомобиля достаточно давить на малый поршень с силой, составляющей лишь 1 % веса автомобиля.
Вычислим давление, оказываемое газом на одну из стенок сосуда (рис. 1.3).

Рис. 1.3
Обозначим: n – концентрация молекул в сосуде; m0 – масса одной молекулы. Движение молекул по всем осям равновероятно, поэтому к одной из стенок сосуда площадью S, подлетает в единицу времени (1/6)nvx молекул, где vx – проекция вектора скорости на направление, перпендикулярное стенке.
Каждая молекула обладает импульсом m0υx, но стенка получает импульс 2m0υx(при абсолютно-упругом ударе m0υx- (-m0υx)=2m0υx). За время dt о стенку площадью S успеет удариться число молекул, которое заключено в объёме V:
| , |
Общий импульс, который получит стенка S:
| , |
Разделив обе части равенства на S и dt, получим выражение для давления:
| , | (1.2.1) |
Таким образом, мы определили давление как силу, действующую в единицу времени на единицу площади:
| , | (1.2.2) |
Наивно полагать, что все молекулы подлетают к стенке S с одной и той же скоростью vx (рис. 1.3). На самом деле молекулы имеют разные скорости, направленные в разные стороны, то есть скорости газовых молекул – случайные величины.
Более точно случайную величину характеризует среднеквадратичная величина. Поэтому под скоростью vx2понимаем среднеквадратичную скорость <vx2> . Вектор скорости, направленный произвольно в пространстве, можно разделить на три составляющих:
| , |
Ни одной из этих проекций нельзя отдать предпочтение из-за хаотичного теплового движения молекул, то есть в среднем . Следовательно, на другие стенки будет точно такое же давление. Тогда можно записать в общем случае:
или
| (1.2.3) |
где <Ek>– средняя энергия одной молекулы. Это и есть основное уравнение молекулярно-кинетической теории газов.
Итак, давление газов определяется средней кинетической энергией поступательного движения молекул.
Уравнение (1.2.3) называют основным уравнением, потому что давление Р – макроскопический параметр системы здесь связан с основными характеристиками – массой и скоростью молекул.
Иногда за основное уравнение принимают выражение
Рассмотрим единицы измерения давления.
По определению, , поэтому размерность давления Н/м2.
1 Н/м2 = 1 Па; 1 атм. = 9,8 Н/см2 = 98066 Па ≈105 Па,
1 мм рт.ст. = 1 тор = 1/760 атм. = 133,3 Па,
1 бар = 105 Па; 1 атм. = 0,98 бар.
Источник
Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.
Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:
- все вещества состоят из мельчайших частиц (молекул, атомов, элементарных частиц), между которыми есть промежутки;
- частицы находятся в непрерывном тепловом движении;
- между частицами вещества существуют силы взаимодействия (притяжения и отталкивания); природа этих сил электромагнитная.
Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.
Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.
Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.
Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.
Существует еще одно состояние вещества – плазма. Плазма – частично или полностью ионизованный газ, в котором плотности положительных и отрицательных зарядов практически одинаковы. При достаточно сильном нагревании любое вещество испаряется, превращаясь в газ. Если увеличивать температуру и дальше, резко усилится процесс термической ионизации, т. е. молекулы газа начнут распадаться на составляющие их атомы, которые затем превращаются в ионы.
Модель идеального газа. Связь между давлением и средней кинетической энергией.
Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.
Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)
Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.
Свойства идеального газа:
- расстояние между молекулами много больше размеров молекул;
- молекулы газа очень малы и представляют собой упругие шары;
- силы притяжения стремятся к нулю;
- взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими;
- молекулы этого газа двигаются беспорядочно;
- движение молекул по законам Ньютона.
Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.
Объем газа обозначается V. Объем газа всегда совпадает с объемом того сосуда, который он занимает. Единица объема в СИ м3.
Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.
p = F/S Единица давления в СИ паскаль [Па]
До настоящего времени употребляются внесистемные единицы давления:
техническая атмосфера 1 ат = 9,81-104 Па;
физическая атмосфера 1 атм = 1,013-105 Па;
миллиметры ртутного столба 1 мм рт. ст.= 133 Па;
1 атм = = 760 мм рт. ст. = 1013 гПа.
Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени действует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.
Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.
Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной.
Приборы, измеряющие давление, называют манометрами. Манометры фиксируют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.
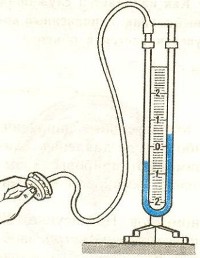
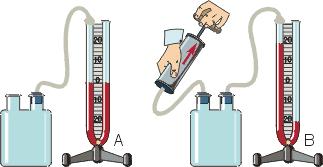
Жидкостные манометры:
- открытый – для измерения небольших давлений выше атмосферного
- закрытый – для измерения небольших давлений ниже атмосферного, т.е. небольшого вакуума

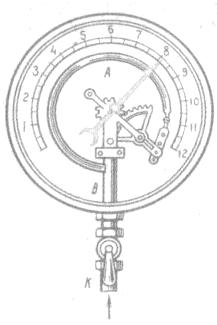
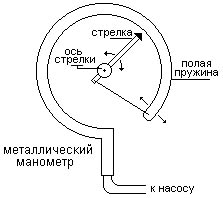
Металлический манометр – для измерения больших давлений.

Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.
Основное уравнение молекулярно-кинетической теории идеального газа.
Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул
p = 1/3·m0·n·v2
m0 – масса одной молекулы газа;
n = N/V – число молекул в единице объема, или концентрация молекул;
v2 – средняя квадратичная скорость движения молекул.
Так как средняя кинетическая энергия поступательного движения молекул E = m0*v2/2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m0· v2)/2 = 2/3·E·n
p = 2/3·E·n
Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.
Так как m0·n = m0·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v2
Объединенный газовый закон.
Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Всякое изменение состояния газа называется термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.
Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
p = nkT
Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
![]()
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим ![]() или
или ![]()
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
![]()
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.
Уравнение Клайперона можно записать в другой форме.
p = nkT,
учитывая, что
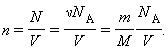
Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
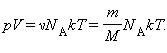
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
Ее численное значение в СИ R = 8,31 Дж/моль·К
Соотношение
![]()
называется уравнением состояния идеального газа.
В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`
Для одного моля любого газа это соотношение принимает вид: pV=RT
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.
Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pSΔh = R
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A.
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.
Источник
