Давление гелия в сосуде формула
11. МКТ и Термодинамика (объяснение явлений)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
На рисунке показана зависимость давления газа (p) от его плотности (rho) в циклическом процессе, совершаемом 2 моль идеального газа в идеальном тепловом двигателе. Цикл состоит из двух отрезков прямых и четверти окружности.
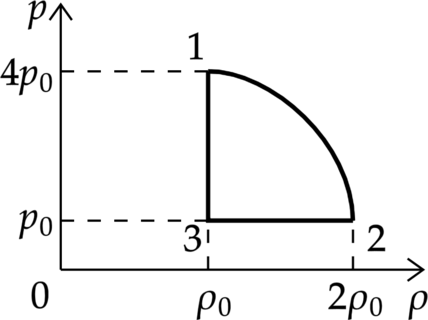
На основании анализа этого циклического процесса выберите два верных утверждения.
1) В процессе 1−2 температура газа уменьшается.
2) В состоянии 3 температура газа максимальна.
3) В процессе 2−3 объём газа уменьшается.
4) Отношение максимальной температуры к минимальной температуре в цикле равно 8.
5) Работа газа в процессе 3−1 положительна.
“Демоверсия 2017”
1) По уравнению Клапейрона – Менделеева: [p=dfrac{rho}{mu}RT,] где (T) – температура, (mu) – молярная масса газа.
Давление уменьшилось в 4 раза, а плотность увеличилась в 2 раза, следовательно, температура уменьшилась в 8 раз.
Утверждение 1 – (color{green}{small text{Верно}})
2) Аналогично предыдущему пункту [p=dfrac{rho}{mu}RT] Максимальная температура будет в состоянии 1 (давление максимально, плотность минимальна)
Утверждение 2 – (color{red}{small text{Неверно}})
3) В процессе 2 – 3 плотность меньшается, а по формуле: [rho =dfrac{m}{V}] Объем увеличивается
Утверждение 3 – (color{red}{small text{Неверно}})
4) Аналогично пункту 2, минимальность температуры будет достигнута в точке с наименьшим давлением и наибольшей плотностью (т. 2), а отношение температур действительно равно 8
Утверждение 4 – (color{green}{small text{Верно}})
5) В процессе 2 – 3 плотность постоянна, следовательно, объем постоянен и газ не совершает работу.
Утверждение 5 – (color{red}{small text{Неверно}})
Ответ: 14
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В начальный момент времени в левой части сосуда содержится 4 моль гелия, в правой – 40 г аргона. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул аргона. Температура газов одинаковая и остаётся постоянной. Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Концентрация гелия в правой части сосуда в 2 раза меньше, чем аргона.
2) Отношение давления газов в правой части сосуда к давлению газа в левой части равно 1,5.
3) В правой части сосуда общее число молекул газов меньше, чем в левой части.
4) Внутренняя энергия гелия и аргона одинакова.
5) В результате установления равновесия давление в правой части сосуда увеличилось в 3 раза.
“Демоверсия 2020”
Перегородка проницаема только для молекул гелия, поэтому в результате установления равновесия парциальное давление гелия в левой части будет равно парциальному давлению гелия в правой части. Давление газа можно вычислить по формуле: [p=dfrac{nu R T}{V}] Парциальные давления гелия в левой и правой части одинаковы, одинаковы температуры и объёмы частей, следовательно, одинаковы и количества вещества гелия в левой и правой частях сосуда, то есть в левой и правой части сосуда будет содержаться по 2 моля гелия.
Найдём связь концентрации и количества вещества: [n=dfrac{N}{V}=dfrac{nu N_A}{V}] То есть концентрации и количества вещества зависят прямо пропорционально друг от друга, также заметим, что чем больше количество вещества, тем больше и количество молекул.
Найдём количество вещества аргона: [nu_{Ar}=dfrac{m_{Ar}}{mu_{Ar}}=dfrac{40text{ г}}{40text{ г/моль}}=1text{ моль}]
Используя полученное выше, рассмотрим данные в задании утверждения.
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
1) (color{red}{small text{Неверно}})
Концентрация гелия в два раза больше концентрации аргона в правой части сосуда
2) (color{green}{small text{Верно}})
Отношение давлений: [dfrac{p_text{ п}}{p_text{ л}}=dfrac{nu_text{ г.п}+nu_{Ar}}{nu_text{ г.л}}=dfrac{2text{ моль}+1text{ моль}}{2text{ моль}}=1,5] Где (nu_{text{ г.п.}},nu_{text{ г.л.}}) – количество вещества гелия в правой части, количество вещества гелия в левой части соответственно.
3) (color{red}{small text{Неверно}})
Количество вещества газов в правой части сосуда больше количества вещества газа в левой части сосуда, следовательно, в правой части сосуда общее число молекул газа больше, чем в левой части сосуда.
4) (color{red}{small text{Неверно}})
Внутренняя энергия одноатомного идеального газа может быть вычислена по формуле: [U=dfrac{3}{2}nu R T] Температура газов одинакова. Количество вещества гелия больше количества вещества аргона, следовательно, внутренняя энергия гелия больше внутренней энергии аргона.
5) (color{green}{small text{Верно}})
айдём отношение конечного давления в правой части сосуда к начальному давлению в правой части сосуда: [dfrac{p_{k}}{p_text{ н}}=dfrac{nu_{text{ г.п.}}+nu_{Ar}}{nu_{Ar}}=dfrac{2text{ моль}+1text{ моль}}{1text{ моль}}=3]
Ответ: 25
В цилиндрическом сосуде под поршнем находится газ. Поршень может перемещаться в сосуде без трения. На дне сосуда лежит стальной шарик (см. рисунок). Газ нагревают.
Выберите из предложенного перечня два верных утверждения, верно описывающие данный процесс, и укажите их номера.
1) Объём газа в этом процессе остаётся неизменным.
2) Давление газа в сосуде остаётся неизменным.
3) Плотность газа в этом процессе увеличивается.
4) Сила Архимеда, действующая на шарик, уменьшается.
5) Концентрация молекул газа в сосуде увеличивается.
1) Так как поршень подвижный (не закреплен), то процесс будет происходить при постоянном давлениии.
Уравнение состояния газа: [pV=nu RT] где (nu) — количество вещества, (T) — температура в Кельвинах, (p) — давление газа, (V) — объем, занимаемый газом, (R) — универсальная газовая постоянная. Выразим объем [V=dfrac{nu RT}{p}] При нагревании газа объем увеличивается.
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Утверждение 2 — (color{green}{smalltext{Верно }})
3) Плотность газа: [rho=dfrac{m}{V}] При нагревании объем увеличивается, значит плотность уменьшается.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Сила Архимеда: [F_{text{Арх}}=rho gV] где (rho) — плотность газа, (V) — объем шарика, (g) — ускорение свободного падения. Плотность уменьшается, значит, сила Архимеда уменьшается.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Концентрация: [n=dfrac{N}{V}] При нагревании газа объем увеличивается, концентрация уменьшается.
Утверждение 5 — (color{red}{smalltext{Неверно }})
Ответ: 24
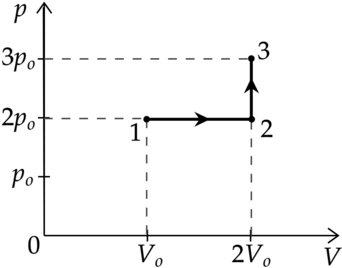
На (pV)—диаграмме отображена последовательность трёх процессов (1 — 2 — 3) изменения состояния 2 моль идеального газа. 
Из предложенного перечня утверждений выберите два правильных и укажите их номера.
1) В процессе 1 газ отдаёт положительное количество теплоты.
2) Процесс 2 является изотермическим.
3) В процессе 3 газ совершает работу.
4) В процессе 2 происходит расширение газа при постоянной температуре.
5) В процессе 1 происходит сжатие газа при постоянной температуре.
Работа газа находится как площадь под графиком 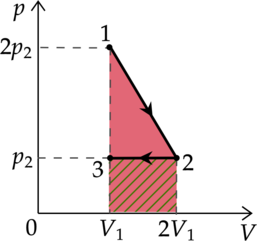
1) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. (Delta U=0), так как температура в процессе 1 не изменяется. При увеличении давления в изотермическом процессе объём уменьшается. (Delta V<0), следоватлеьно, (A<0). Таким образом, (Q<0), то есть газ отдает кол-во теплоты в данном процессе.
Утверждение 1 — (color{green}{smalltext{Верно }})
2) В процессе 2 температура увеличивается.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) (p=const), следовательно (Vsim T)
Температура уменьшается, то есть объем тоже уменьшается, (Delta V<0), (A<0)
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В процессе 2 температура увеличивается.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Температура в процессе 1 не изменяется. По закону Бойля-Мариотта (p V=const) так как давление увеличивается объём уменьшается.
Утверждение 5 —(color{green}{smalltext{Верно }})
Ответ: 15
На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах (V-T), где (V) — объём газа, (T) — абсолютная температура газа. Количество вещества газа постоянно. 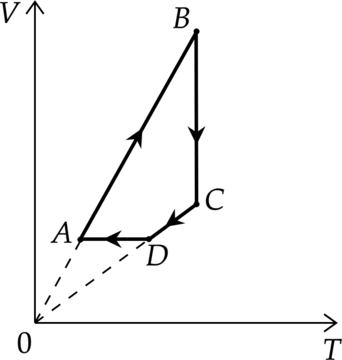
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) В состоянии (B) концентрация газа максимальна.
2) В процессе (AB) газ отдаёт некоторое количество теплоты.
3) В процессе (BC) внутренняя энергия газа увеличивается.
4) Давление газа в процессе (CD) постоянно, при этом внешние силы совершают над газом положительную работу.
5) В процессе (DA) давление газа изохорно уменьшается.
1) В точке (B) объем максимален, а концентрация минимальна:
Утверждение 1 —(color{red}{smalltext{Неверно }})
2) Первое начало термодинамики: [Q=Delta U+A] где (Delta U) — изменение внутренней энергии, (A) — работа газа, (Q) — количество теплоты, полученное газом. В процессе (AB) работа равна (0), температура увеличивается, то есть (Delta U>0), значит (Q>0), то есть газ получает тепло
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс (BC) — изотермический. Внутренняя энергия не меняется.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) Процесс (СD) — изобарное сжатие. При уменьшении объема внешние силы совершают положительную работу.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) Процесс (DA) — изохорное охлаждение ((psim T)). Следовательно, при уменьшении температуры давление уменьшается.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Идеальный газ перевели из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не менялось. 
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
1)Абсолютная температура газа минимальна в состоянии 2.
2)В процессе 1-2 абсолютная температура газа уменьшилась в 2 раза.
3)В процессе 2-3 абсолютная температура газа уменьшилась в 1,5 раза.
4)Плотность газа максимальна в состоянии 1.
5)В ходе процесса 1-2-3 средняя квадратичная скорость теплового движения молекул газа увеличилась в (sqrt{3}) раза.
1) Уравнение состояния газа: [pV=nu RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещеста, (R) — универасальная газовая постоянная, (T) — температура. Температура максимальна там, где максимально произведение (pV), поэтому из графика видно, что (T_1 – min), (T_3 – max), (T_1<T_2<T_3)
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) Процесс 1-2 — изобарное расширение ((Vsim T)). Объем увеличился в 2 раза, то есть температура тоже увеличилась в 2 раза.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Процесс 2-3 — изохорное нагревание. (V=const), следовательно (psim T) Давление увеличивается в 1,5 раза, то есть температура тоже увеличивается в 1,5 раза.
Утверждение 3 — (color{red}{smalltext{Неверно }})
4) В точке 1 — объем минимален, следовательно, плотность там максимальна.
Утверждение 4 — (color{green}{smalltext{Верно }})
5) [E_{k}=dfrac{3}{2}kT] [dfrac{m_0 v^2}{2}=dfrac{3}{2}kT] где (m_0) — масса газа, (v^2) средняя квадратичная скорость [v^2sim T] [vsim sqrt{T}] Температура в процессе 1-2-3 увеличилась в 3 раза, значит средняя квадратичная скорость увеличилась в (sqrt{3}) раз
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 45
Сосуд разделён на две равные по объёму части пористой неподвижной перегородкой. В левой части сосуда содержится 40 г неона, в правой — 2 моль гелия. Перегородка может пропускать молекулы гелия и является непроницаемой для молекул неона. Температура газов одинакова и остаётся постоянной.
Выберите два верных утверждения, описывающих состояние газов после установления равновесия в системе.
1) Внутренняя энергия гелия в сосуде меньше, чем внутренняя энергия неона.
2) Концентрация гелия в левой части сосуда в 2 раза больше концентрации неона.
3) В левой части сосуда общее число молекул газов в 3 раза больше, чем в правой части.
4) Внутренняя энергия гелия в сосуде в конечном состоянии меньше, чем в начальном.
5) В конечном состоянии давление в левой части сосуда в 3 раза больше, чем в правой.
1) Молярная масса неона (M=20) г/моль. Количество неона: [nu=dfrac{m}{M}=dfrac{40text{ г}}{20text{ г/моль}}=2 text{ моль}] Гелий займет все пространство сосуда, значит в левой части будет 3 моля вещества (1 моль гелия и 2 моль неона).
В правой части будет тоже 1 моль гелия.
Внутренняя энергия газа: [U=dfrac{i}{2}nu RT] Газы находятся при одинаковой температуре, количество гелия равно количеству неона. Внутренняя энергия гелия равна внутренней энергии неона
Утверждение 1 — (color{red}{smalltext{Неверно }})
2) В левой части сосуда количество гелия в два раза меньше количества неона. Следовательно, концентрация гелия в два раза меньше концентрации неона.
Утверждение 2 — (color{red}{smalltext{Неверно }})
3) Так как количество вещества в левой части сосуда больше в 3 раза, чем в правой, то и количество молекул также больше в 3 раза.
Утверждение 3 — (color{green}{smalltext{Верно }})
4) Так как температура гелия и общее количество гелия в сосуде не изменилось, то и внутреннняяя энергия не поменялась.
Утверждение 4 — (color{red}{smalltext{Неверно }})
5) Давление газа: [p=nkT] Так как кол-во вещества в левой части сосуда больше в 3 раза, чем в правой, температуры одинаковые, то давление в конечном состоянии больше в левой части в 3 раза, чем в правой.
Утверждение 5 — (color{green}{smalltext{Верно }})
Ответ: 35
Источник
Жи́дкий ге́лий — жидкое агрегатное состояние гелия. Представляет собой бесцветную прозрачную жидкость, кипящую при температуре 4,2 К (для изотопа 4He при нормальном атмосферном давлении)[1][2]. Плотность жидкого гелия при температуре 4,2 К составляет 0,13 г/см³. Обладает малым показателем преломления, из-за чего его трудно увидеть.
При определённых условиях жидкий гелий представляет собой квантовую жидкость, то есть жидкость, в макроскопическом объёме которой проявляются квантовые свойства составляющих её атомов. Из-за квантовых эффектов (нулевые колебания), при нормальном давлении гелий не затвердевает даже при абсолютном нуле. Твёрдый гелий в α-фазе удаётся получить лишь при давлении выше 25 атм.
История исследований[править | править код]
История получения и исследований жидкого гелия тесно связана с историей развития криогеники.
- В 1898 году Дьюаром получено около 20 см³ жидкого водорода.
- В 1906 году Камерлинг-Оннес наладил линию полупромышленного получения жидкого водорода, дающую до 4 литров в час.
- В 1908 году он же сумел добиться конденсации жидкого гелия в объёме 0,06 литра (Нобелевская премия по физике за 1913 год). Для опыта потребовалось 20 литров жидкого водорода, полученного при помощи линии, созданной двумя годами ранее. Низкие температуры, необходимые для конденсации гелия, были достигнуты при адиабатическом дросселировании водорода (см. эффект Джоуля — Томсона).
- В 1930 году[3]Виллем Хендрик Кеезом обнаружил наличие фазового перехода в жидком гелии при температуре 2,17 К и давлении насыщенных паров 0,005 МПа. Он назвал фазу, устойчивую выше температуры 2,17 K, гелием-I, а фазу, устойчивую ниже этой температуры — гелием-II. Также он наблюдал связанные с этим аномалии в теплопроводности (и даже называл гелий-II «сверхтеплопроводным»), теплоёмкости, текучести гелия.
- В 1938 году П. Л. Капица открыл сверхтекучесть гелия-II (Нобелевская премия по физике за 1978 год). Квантовомеханическое объяснение явления было дано Л. Д. Ландау в 1941 году (Нобелевская премия по физике за 1962 год).
- В 1948 году удалось сжижить и гелий-3.
- В 1972 году в жидком гелии-3 также был обнаружен фазовый переход. Позже было экспериментально показано, что ниже 2,6 мК и при давлении 34 атм гелий-3 действительно становится сверхтекучим. (Нобелевская премия по физике за 2003 год.)
Физические свойства[править | править код]
Физические свойства гелия сильно отличаются у изотопов 4He и 3He:
| Свойство | 4He | 3He | |
|---|---|---|---|
| Температура плавления, К | 2,0 (при 3,76 МПа) | 1,0 (при 3,87 МПа) | |
| Температура кипения, К | 4,215 | 3,19 | |
| Минимальное давление плавления, атм | 25 | 29 (0,3 K) | |
| Плотность газообразного, кг/м³ | 0,178 | 0,134 | |
| Плотность жидкого, кг/м³ | 145 (при 0 К) | 82,35 | |
| Крит. точка | tкрит, К | 5,25 | 3,35 |
| pкрит, МПа | 0,23 | 0,12 | |
| dкрит, кг/м³ | 69,3 | 41,3 | |
Свойства гелия-4[править | править код]
Жидкий гелий — бозе-жидкость, то есть жидкость, частицы которой являются бозонами.
Выше температуры 2,17 К гелий-4 ведёт себя как обычная криожидкость, то есть кипит, выделяя пузырьки газа. При достижении температуры 2,17 К (при давлении паров 0,005 МПа — так называемая λ-точка) жидкий 4Не претерпевает фазовый переход второго рода, сопровождающийся резким изменением ряда свойств: теплоёмкости, вязкости, плотности и других. В жидком гелии при температуре ниже температуры перехода одновременно сосуществуют две фазы, Не I и Не II, с сильно различающимися свойствами. Состояние жидкости в фазе гелия-II в некоторой степени аналогично состоянию бозе-конденсата (однако, в отличие от конденсата атомов разреженного газа, взаимодействие между атомами гелия в жидкости достаточно сильно, поэтому теория бозе-конденсата неприменима впрямую к гелию-II).
Сверхтекучесть и сверхтеплопроводность[править | править код]
Фазовый переход в гелии хорошо заметен, он проявляется в том, что кипение прекращается, жидкость становится совершено прозрачной. Испарение гелия, конечно, продолжается, но оно идёт исключительно с поверхности. Различие в поведении объясняется необычайно высокой теплопроводностью сверхтекучей фазы (во много миллионов раз выше, чем у Не I). При этом вязкость нормальной фазы остаётся практически неизменной, что следует из измерений вязкости методом колеблющегося диска. С увеличением давления температура перехода смещается в область более низких температур. Линия разграничения этих фаз называется λ-линией.
Для He II характерна сверхтекучесть — способность протекать без трения через узкие (диаметром менее 100 нм) капилляры и щели. Относительное содержание He II растет с понижением температуры и достигает 100 % при абсолютном нуле температуры — с этим были связаны попытки получения сверхнизких температур путём пропускания жидкого гелия через очень тонкий капилляр, через который пройдет только сверхтекучая компонента. Однако за счёт того, что при близких к абсолютному нулю температурах теплоёмкость также стремится к нулю, добиться существенных результатов не удалось — за счёт неизбежного нагрева от стенок капилляра и излучения.
За счёт сверхтекучести и достигается аномально высокая теплопроводность жидкого гелия — теплопередача идёт не за счёт теплопроводности, а за счёт конвекции сверхтекучей компоненты в противоток нормальной, которая переносит тепло (сверхтекучая компонента не может переносить тепло). Это свойство открыто в 1938 году П. Л. Капицей.
Второй звук[править | править код]
За счёт одновременного наличия двух фаз в жидком гелии, имеется две скорости звука и специфическое явление — так называемый «второй звук». Второй звук — слабозатухающие колебания температуры и энтропии в сверхтекучем гелии. Скорость распространения второго звука определяется из уравнений гидродинамики сверхтекучей жидкости в двухкомпонентной модели. Если пренебречь коэффициентом теплового расширения (который у гелия аномально мал), то в волне второго звука осциллируют только температура и энтропия, а плотность и давление остаются постоянными. Распространение второго звука не сопровождается переносом вещества.
Второй звук можно также интерпретировать как колебания концентрации квазичастиц в сверхтекучем гелии. В чистом 4He это колебания в системе ротонов и фононов.
Существование второго звука было предсказано теоретически Ландау; расчётное значение равнялось 25 м/с. Фактически измеренное значение составляет 19,6 м/с[4].
Свойства гелия-3[править | править код]
Фазовая диаграмма гелия-3
Фазовая диаграмма раствора гелия-3 в гелии-4
Жидкий гелий-3 — это ферми-жидкость, то есть жидкость, частицы которой являются фермионами. В таких системах сверхтекучесть может осуществляться при определённых условиях, когда между фермионами имеются силы притяжения, которые приводят к образованию связанных состояний пар фермионов — так называемых куперовских пар (эффект Купера).
Куперовская пара обладает целым спином, то есть ведёт себя как бозон; поэтому вещество, состоящее из объединённых в куперовские пары фермионов, может переходить в состояние, подобное бозе-конденсату. Сверхтекучесть такого рода осуществляется для электронов в некоторых металлах и носит название сверхпроводимости.
Аналогичная ситуация имеет место в жидком 3He, атомы которого имеют спин ½ и образуют типичную квантовую ферми-жидкость. Свойства жидкого гелия-3 можно описать как свойства газа квазичастиц-фермионов с эффективной массой примерно в 3 раза большей, чем масса атома 3He. Силы притяжения между квазичастицами в 3He очень малы, лишь при температурах порядка нескольких милликельвинов в 3He создаются условия для образования куперовских пар квазичастиц и возникновения сверхтекучести. Открытию сверхтекучести у 3He способствовало освоение эффективных методов получения низких температур — эффекта Померанчука и магнитного охлаждения. С их помощью удалось выяснить характерные особенности диаграммы состояния 3He при сверхнизких температурах.
Переход нормальной ферми-жидкости в фазу А представляет собой фазовый переход II рода (теплота фазового перехода равна нулю). В фазе A образовавшиеся куперовские пары обладают спином 1 и отличным от нуля моментом импульса. В ней могут возникать области с общими для всех пар направлениями спинов и моментов импульса. Поэтому фаза А является анизотропной жидкостью. В магнитном поле фаза А расщепляется на две фазы (A1 и A2), каждая из которых также является анизотропной. Переход из сверхтекучей фазы А в сверхтекучую фазу В является фазовым переходом I рода с теплотой перехода около 1,5⋅10−6 дж/моль. Магнитная восприимчивость 3He при переходе А→В скачком уменьшается и продолжает затем уменьшаться с понижением температуры. Фаза В является, по-видимому, изотропной.
Хранение и транспортировка[править | править код]
Как и другие криожидкости, гелий хранят в сосудах Дьюара. Гелий в них всегда хранится под небольшим давлением — за счёт естественного испарения жидкости. Это позволяет в случае небольшой негерметичности не допустить загрязнения гелия. Избыточное давление стравливается через клапан. На практике, так как гелий достаточно дорог, то, чтобы не выпускать газ в атмосферу, на головной части дьюара размещается соединительная часть для подсоединения дьюара к гелиевой сети, по которой газообразный гелий собирается для повторного использования. Как правило, на этом же узле крепится манометр для контроля давления и аварийный клапан.
Гелиевые дьюары переворачивать нельзя, для переливания содержимого применяют специальные сифоны.
Гелий имеет очень низкую теплоту испарения (в 20 раз меньше, чем у водорода), но зато высокую теплопроводность. Поэтому к качеству теплоизоляции гелиевых дьюаров предъявляются высокие требования. При повреждении вакуумной изоляции жидкость так бурно вскипает, что дьюар может взорваться. Как правило, для снижения потерь гелия на испарение используется «азотная рубашка» — непосредственно в вакуумной полости сосуда Дьюара расположена ещё одна оболочка, которая охлаждается кипящим жидким азотом (температура 77 К). За счёт этого удается существенно сократить теплообмен между гелием и атмосферой.
Жидкий гелий перевозят в специальных транспортных сосудах, выпускаемыми промышленно. В СССР и позднее в России выпускались сосуды типа СТГ-10, СТГ-25, СТГ-40 и СТГ-100 ёмкостью 10, 25, 40 и 100 литров, соответственно. Эти сосуды широко используются в российских лабораториях и в настоящее время. Сосуды с жидким гелием должны транспортироваться и храниться в вертикальном положении.
Применение жидкого гелия[править | править код]
Современный ЯМР-томограф. Для охлаждения сверхпроводящих магнитов в нём используется жидкий гелий.
Жидкий гелий применяется в качестве хладагента для получения и поддержания низких и сверхнизких температур (в основном в научных исследованиях):
- охлаждение сверхпроводящих магнитов в различных научных, технических и медицинских устройствах, к примеру:
- ускорители заряженных частиц
- В Большом адронном коллайдере в ЦЕРНе используется 96 тонн жидкого гелия для охлаждения 1624 сверхпроводящих магнитов до температуры 1,9 K[5]
- детекторы инфракрасного и высокочастотного излучения, сквид-магнетометры;
- сканирующие туннельные микроскопы;
- ускорители заряженных частиц
- использование в криостатах растворения[прояснить];
- криогенные электрические машины[прояснить].
Примечания[править | править код]
Ссылки[править | править код]
Научно-популярные ресурсы[править | править код]
- Свойства жидкого гелия — доклад академика П. Л. Капицы, «Природа», N12, 1997.
Книги, обзорные статьи[править | править код]
- Сверхтекучий 3He: ранняя история глазами теоретика — нобелевская лекция Э. Дж. Леггетта, УФН, т. 174, № 11, 2003 г.
- Воловик Г., «Universe in a helium droplet», Oxford University Press, 2004, 529 стр., книга доступна на сайте автора (PDF, 3,5 Мб).
Источник
