Давление идеального газа в сосуде обусловлено
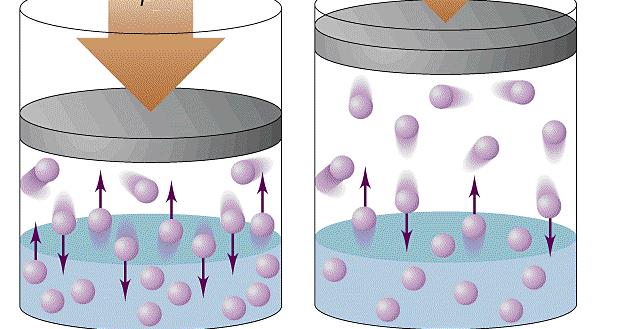
Давление газа — что это за параметр
Определение
Давление в физике представляет собой один из трех ключевых термодинамических макроскопических характеристик для измерения любой газовой системы.
Определение
Газ — это одно из четырех, включая плазму, агрегатных состояний материи, характеризующееся очень слабыми связями между составляющими его частицами, а также их большой подвижностью.
В газообразной среде частицы в определенной концентрации расположены не упорядоченно и перемещаются в хаотичном порядке в разных направлениях с одинаковой вероятностью. Подобное строение не позволяет газам сохранять стабильность объема и формы даже при малом внешнем силовом воздействии. Для любого газа, включая одноатомный, значение средней кинетической энергии его частиц в виде атомов и молекул будет превышать энергию межмолекулярного взаимодействия между ними.
Кроме того, расстояние, на которое удалены частицы, значительно превышает их собственные размеры. В том случае, когда молекулярными взаимодействиями и габаритами частиц допускается пренебрегать, газ считают идеальным. Для такой формы материи характерен только один тип внутреннего взаимодействия в виде упругих столкновений. Так как размер частиц пренебрежимо мал по сравнению с расстоянием, на которое они удалены, вероятность столкновений частиц между собой будет низкой.
Примечание
По этой причине в идеальной газовой среде можно наблюдать лишь столкновения частиц со стенками сосуда. Какой-либо реальный газ с хорошей точностью можно отнести к идеальному, когда их температура выше, чем комнатная, а давление несущественно больше, чем атмосферное.
Причина возникновения давления в газах
Давление газа нельзя объяснить теми же причинами, что и давление твердого тела на опору. Расстояние, на которое удалены молекулы газообразной среды, существенно больше. В результате хаотичного движения они сталкиваются между собой и со стенками сосуда, который они занимают. Давление газа на стенки сосуда и вызвано ударами его молекул.
Данный параметр увеличивается по мере того, как нарастает сила ударов молекул о стенки. Газ характеризуется одинаковым давлением во всех направлениях, которое является следствием хаотичного движения огромного числа молекул.
Примечание
Важно отметить, что газ оказывает давление на дно и стенки сосуда, объем которого он занимает, во всех направления равномерно. В связи с этим, воздушный шарик сохраняет форму, несмотря на то, что его оболочка достаточно эластична.
Перед тем как транспортировать или отправить на хранение газообразные вещества, их сильно сжимают. В этом случае давление газа увеличивается. Его помещают в специальные баллоны из стали высокой прочности. Такие емкости необходимы для хранения сжатого воздуха на подводных лодках и кислорода, предназначенного для сварки металлов.
Свойства давления газа:
- Если объем уменьшается, то давление газа возрастает, а во время увеличения объема, давление будет снижаться при постоянных величинах массы и температуры вещества.
- Газ, находящийся в закрытом сосуде, характеризуется давлением, которое возрастает по мере увеличения температуры вещества при условии постоянства его массы и объема.
- В том случае, когда масса газа увеличивается, его давление также будет возрастать и наоборот.

Запись формул для определения давления газа начинают с выяснения причин, по которым оно возникает в рассматриваемой системе. Исходя из физического смысла, давление представляет собой величину, равную отношению силы, перпендикулярно воздействующей на некоторое основание, к площади этого основания:
(P=frac{F}{S})
Как было отмечено ранее, для идеальной газовой системы характерен лишь один тип взаимодействия — это абсолютно упругие столкновения. В процессе частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. В данном случае применим второй закон Ньютона:
(F*Δt = Δp)
Таким образом, конкретно сила F является причиной формирования давления на стенки сосуда. Данная величина F, производимая одной частицей, незначительна. Однако, когда количество частиц огромно, они в совокупности создают ощутимый эффект, проявляемый в виде наличия давления в сосуде.
Формула давления идеального газа из молекулярно-кинетической теории
Объяснение концепции идеального газа построено на основных положениях молекулярно-кинетической теории, которая вытекает из принципов статистической механики. Наука получила активное развитие во второй половине XIX, благодаря таким ученым, как Джеймс Максвелл и Людвиг Больцман. Основы дисциплины были заложены еще Бернулли в первой половине XVIII века.

Исходя из статистики Максвелла-Больцмана, все частицы в системе обладают разными скоростями движения. При этом можно наблюдать небольшой процент частиц со скоростями, приближенными к нулю, и малую долю частиц, обладающих огромной скоростью. Средняя квадратичная скорость в этом случае будет соответствовать некоторой величине, не изменяющейся с течением времени.
Средняя квадратичная скорость частиц однозначно характеризует температуру газа. Используя приближения молекулярно-кинетической теории в виде невзаимодействующих безразмерных и хаотично движущихся частиц, получают формулу для расчета давления газа в сосуде:
(P=frac{N*m*v^{2}}{3*V})
где N является количеством частиц в системе; V обозначает объем; v представляет собой среднюю квадратичную скорость; m является массой одной частицы.
При наличии указанных в формуле параметров, выраженных в единицах СИ, можно вычислить давление газа в сосуде.
Второй способ записи основного уравнения МКТ
Определение
В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:
(P*V = n*R*T )
n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.
Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.
Определение
С помощью данного выражения можно определить формулу для расчета давления газа:
(P=frac{n*R*T}{V})
Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.

Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.

Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m. В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:
- Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
- Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример
Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.
Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:
(P=frac{N*m*v^{2}}{3*V})
Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:
(m=frac{M}{NA})
(n=frac{N}{NA})
(m*N= M*n)
(P=frac{M*n*v^{2}}{3*V})
Таким образом, удельный объем сосуда в кубических метрах равен 0,01. Молярная масса молекулы кислорода М составляет 0,032 кг/моль. Данные параметры можно подставить в уравнение вместе со скоростью и количеством вещества. Тогда Р = 533333 Па, что представляет собой давление в 5,3 атмосферы.
Источник
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
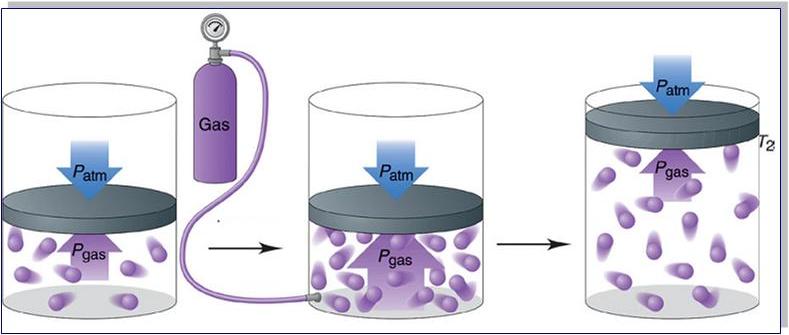
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
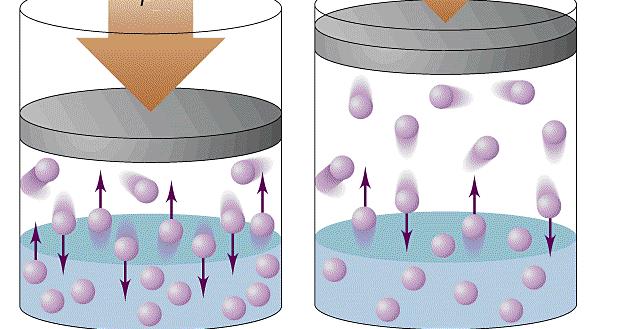
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
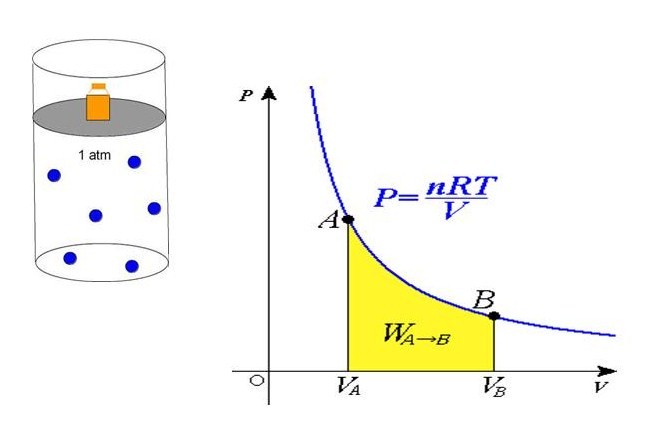
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
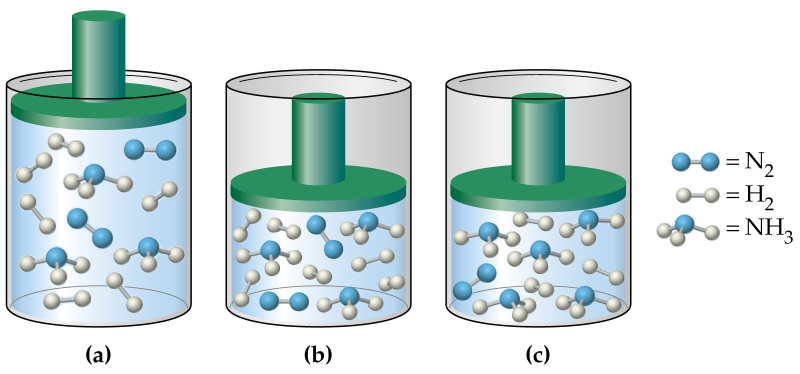
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Как объясняют давление газа на основе учения о движении молекул?
Давление газа на стенки сосудов вызывается ударами молекул газа.
У газов нет ни формы ни постоянного объема. Они могут заполнить любой объем.
Количество молекул в каждом кубическом сантиметре увеличивается при сжатии (уменьшается при расширении) от этого число ударов о стенки сосуда увеличивается (уменьшается). Поэтому чем больший сосуд газ заполняет, тем меньше давление и наоборот.
Газ одинаково давит по всем направлениям, как пример -когда надуваешь воздушный шар, то он надувается равномерно.
Если газ находиться в маленьком объеме, то давление на стенки становится огромным, поэтому газ удобнее и безопаснее заключать в специальные прочные стальные баллоны.
Давление газа вызывается ударами молекул о стенки сосуда, т.к. молекулы хаотически движутся и постоянно соударяются друг с другом и со всеми встреченным препятствиями.
Теория квантового поля позволяет вселенной появиться из ниоткуда?
В статье » Возможно ли появление Вселенной из ничего»известный российский физик-космолог Я.Б.Зельдович дал исчерпывающий ответ на этот вопрос. Я склоняюсь перед таким научным авторитетом и полностью разделяю его точку зрения на этот вопрос
1 4 · Хороший ответ
Почему сильные взрывы (атомный) не сбивают Землю с орбиты, не меняют скорость прокрутки вокруг своей оси?
Примерно по той же причине, по которой вы не падаете на спину при каждом выдохе.
Так как вы выдыхаете некоторую массу воздуха, согласно второму закону Ньютона на вас действует некоторая реактивная сила. Но ваша масса настолько велика, что результирующее ускорение (сила, делённая на вашу массу) оказывается ничтожно малым. Но в реальном мире даже этого ничтожного ускорения вы не испытываете, потому что этой силы недостаточно для того, чтобы преодолеть силы трения (обо всё) и вашу неупругость.
То же самое и с Землёй: для того, чтобы сдвинуть такой массивный и неупругий шар как Земля нужно нечто более серьёзное чем атомный чих.
4 0 · Хороший ответ
По Эйнштейну, чем ближе тело или частица к скорости света, тем огромнее становится его масса. И вот,в Большом адронном коллайдере, протоны и ионы, движутся почти со скоростью света, и что это значит?
Релятивистской массы нет в природе и, согласно релятивистской механике Эйнштейна, масса остаётся инвариантной и равной массе покоя всегда, независимо от скорости (недоверчивым сюда).
Темп роста энергии частицы (E) с ростом скорости β = v/c (в единицах скорости света c) получен мною здесь. Если тело обладало скоростью β₁ = 0,9 при энергии Е₁, то для достижения скорости β₂ = 0,9. 999 (n девятoк после запятой), потребуется энергия E₂ = (3,16)ⁿ⁻¹⋅Е₁. Получается, что с каждой новой девяткой в величине скорости (β), энергия должна быть увеличена в 3,16 раз. Таким образом, неограниченный рост числа девяток (n) в численном значении скорости (β), приводит к неограниченному росту энергии.
Mаксимальная скорость зарегистрированного материального объекта (протона), ускоренного до околосветовых скоростей в космическом пространстве, равна β = 0,9. 999 (всего 23 девятки), а соответствующая энергия, E
10¹¹ ГэВ. Области в галактиках и механизмы ускорения до этих скоростей пока неизвестны. Максимальные энергии столкновения протонов, достигнутые на ускорителе БАК (LHC) в ЦЕРН, равны 1,3×10⁴ ГэВ, что в системе отсчёта неподвижной мишени соответствует энергии протона = 9×10⁷ ГэВ или скорости протона β = 0,999 999 999 999 9999 (16 девяток). В обоих случаях масса протона остаётся неизменной и равной массе покоя, 0.938 ГэВ.
Согласно релятивистской механике, со скоростью света (β = 1) могут лететь только безмассовые частицы (фотоны), но и у них есть недостаток − они не могут лететь медленнее.
1 8 · Хороший ответ
Какое давление на стенки сосуда производят молекулы газа?
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Концентрацию молекул газа n находят как отношение числа молекул N к объему газа V:
Произведение массы одной молекулы m0 на количество молекул N по смыслу есть масса газа m, поэтому:
Подставив в эту формулу исходные данные, можно вычислить какое давление на стенки сосуда производят молекулы газа.
Почему по представлениям астрофизиков сразу после Большого Взрыва фотоны могли двигаться со сверх световой скоростью?
Нету таких представлений у астрофизиков. Свет в вакууме всегда распространяется с одной и той же скоростью c=299 792 458 м/с. Если свет распространяется в какой-то среде, то его скорость будет меньше.
Возможно, Вы путаете с так называемым сверхсветовым расширением Вселенной, при котором расстояния между достаточно удалёнными объектами могут увеличиваться со скоростью, большей скорости света. Но при таком расширении никакие объекты не движутся быстрее света. «Просто» пространство между ними «растягивается». Это трудно себе представить, но расширение Вселенной происходит не потому, что вокруг неё есть пустое пространство, в которое разлетаются все космические объекты, а потому, что «растягивается» пространство между объектами. При этом пространство между связанными объектами (например, между Солнцем и планетами) не «растягивается».
Вообще, «Большой Взрыв» — это совсем не взрыв. При взрыве происходит быстрое выделение энергии в ограниченном объёме пространства, температура и давление в этом объёме резко возрастают, и из-за разницы давлений внутри и снаружи вещество начинает разлетаться. При «Большом Взрыве» нет ни выделения энергии, ни разницы давлений, ни самого «окружающего» пространства. Вещество «разлетается» по инерции, постепенно тормозясь взаимным притяжением.
Как показывают наблюдения, существует также неизвестная причина, вызывающая отталкивание объектов, которое начинает преобладать над притяжением, когда плотность вещества во Вселенной становится достаточно малой. На притяжение достаточно близких объектов (например, тел Солнечной системы или звёзд в Галактике) эта причина сколько-нибудь заметного влияния не оказывает.
Источник
Давление газа. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона). Изопроцессы
Давление газа обозначается буквой р, измеряемся в Паскалях (Ньютон делить на метр в квадрате). Давление газа обусловлено ударами молекул о стенки сосуда. Чем чаше удары, чем они сильнее – тем выше давление.
Идеальный газ – это модель в физике. За идеальный газ принимают газ в сосуде, когда молекула, пролетая от стенки до стенки сосуда не испытывает столкновения с другими молекулами.
Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).
, где — концентрация, 1/моль; — масса молекулы, кг; — средняя квадратичная скорость молекул, м/с; — кинетическая энергия движения молекул, Дж.
Уравнение состояния идеального газа — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
. Такое уравнение носит название уравнение Клайперона-Менделеева.
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака. Эти законы называют законами для изопроцессов:
Изопроцессы – это процессы, которые совершаются при одинаковом параметре или Т-температуре, или V-объеме, или р-давлении.
Изотермический процесс —
— закон Бойля — Мариотта (при постоянной температуре и данной массы газа произведение давления на объем есть величина постоянная)
Изобарный процесс —
— закон Гей-Люссака (при постоянном давлении для данной массы газа отношение объема к температуре есть величина постоянная)
Изохорный процесс —
— закон Шарля (при постоянном объеме для данной массы газа отношение давления к температуре есть величина постоянная)
10/2. Проверка зависимости периода колебания нитяного маятника от длины нити (и независимости периода от массы груза)
В вашем распоряжении имеются штатив, к лапке которого привязана нить длиной 100 см с грузом массой 0,1 кг, набор грузов массой по 0,1 кг, секундомер.
Измерьте период колебаний груза при начальном отклонении его от положения равновесия на 5 см. Подвесьте к нити еще один груз массой 0,1кг и снова измерьте период колебаний. Подтверждают ли результаты опытов предположение о том, что период также увеличился в два раза?
Измерьте период колебаний маятника с одним грузом и нитью длиной 100 см при начальном отклонении его от положения равновесия на 5 см. Уменьшите длину нити до 25 см и снова измерьте период колебаний маятника. Подтверждают ли результаты опытов предположение о том, что при уменьшении длины нити в 4 раза период колебаний уменьшается в 2 раза?
БИЛЕТ-11 11
Испарение и конденсация. Насыщенные и ненасыщенные пары. Влажность воздуха. Измерение влажности воздуха.
Испарение — парообразование, происходящее при любой температуре со свободной поверхности жидкости. Неравномерное распределение кинетической энергии молекул при тепловом движении приводит к тому, что при любой температуре кинетическая энергия некоторых молекул жидкости или твердого тела может превышать потенциальную энергию их связи с другими молекулами. Большей кинетической энергией обладают молекулы, имеющие большую скорость, а температура тела зависит от скорости движения его молекул, следовательно, испарение сопровождается охлаждением жидкости. Скорость испарения зависит: от площади открытой поверхности, температуры, концентрации молекул вблизи жидкости. Конденсация — процесс перехода вещества из газообразного состояния в жидкое.
Испарение жидкости в закрытом сосуде при неизменной температуре приводит к постепенному увеличению концентрации молекул испаряющегося вещества в газообразном состоянии. Через некоторое время после начала испарения концентрация вещества в газообразном состоянии достигнет такого значения, при котором число молекул, возвращающихся в жидкость, становится равным числу молекул, покидающих жидкость за то же время. Устанавливается динамическое равновесие между процессами испарения и конденсации вещества. Вещество в газообразном состоянии, находящееся в динамическом равновесии с жидкостью, называют насыщенным паром. (Паром называют совокупность молекул, покинувших жидкость в процессе испарения.) Пар, находящийся при давлении ниже насыщенного, называют ненасыщенным.
Вследствие постоянного испарения воды с поверхностей водоемов, почвы и растительного покрова, а также дыхания человека и животных в атмосфере всегда содержится водяной пар. Поэтому атмосферное давление представляет собой сумму давления сухого воздуха и находящегося в нем водяного пара. Давление водяного пара будет максимальным при насыщении воздуха паром. Насыщенный пар в отличие от ненасыщенного не подчиняется законам идеального газа. Так, давление насыщенного пара не зависит от объема, но зависит от температуры. Эта зависимость не может быть выражена простой формулой, поэтому на основе экспериментального изучения зависимости давления насыщенного пара от температуры составлены таблицы, по которым можно определить его давление при различных температурах.
Давление водяного пара, находящегося в воздухе при данной температуре, называют абсолютной влажностью, или упругостью водяного пара. Поскольку давление пара пропорционально концентрации молекул, можно определить абсолютную влажность как плотность водяного пара, находящегося в воздухе при данной температуре, выраженную в килограммах на метр кубический (р).
Большинство явлений, наблюдаемых в природе, например быстрота испарения, высыхание различных веществ, увядание растений, зависит не от количества водяного пара в воздухе, а от того, насколько это количество близко к насыщению, т. е. от относительной влажности, которая характеризует степень насыщения воздуха водяным паром. При низкой температуре и высокой влажности повышается теплопередача и человек подвергается переохлаждению. При высоких температурах и влажности теплопередача, наоборот, резко сокращается, что ведет к перегреванию организма. Наиболее благоприятной для человека в средних климатических широтах является относительная влажность 40—60%. Относительной влажностью называют отношение плотности водяного пара (или давления), находящегося в воздухе при данной температуре, к плотности (или давлению) водяного пара при той же температуре, выраженное в процентах, т. е.
11/2. Экспериментальное задание по теме «Электромагнитная индукция»:
наблюдение явления электромагнитной индукции.
В вашем распоряжении имеется оборудование для исследования явления электромагнитной индукции: магнит, проволочная катушка, миллиамперметр.
Подключите миллиамперметр к катушке, исследуйте возможные способы получения индукционного тока в катушке. Сделайте вывод об условиях, при которых возникает электрический ток.
11. Работа в термодинамике. Внутренняя энергия. Первый закон термодинамики. Адиабатный процесс. Второй закон термодинамики.
Как известно, особенность сил трения состоит в том, что работа, совершенная против сил трения, не увеличивает ни кинетическую, ни потенциальную энергию. Однако, работа против сил трения не проходит бесследно. Например, движение тела при наличии сопротивления воздуха приводит к увеличению температуры тела. Это увеличение иногда может быть очень велико — метеориты, влетающие в атмосферу, сгорают в ней именно благодаря нагреванию, вызванному сопротивлением воздуха. Также при движении с наличием сил трения может происходить изменение состояния тела — плавление и др.
Итак, если движение происходит при наличии сил трения, то, во-первых, происходит уменьшение суммы кинетической и потенциальной энергии всех тел, участвующих в процессе, во-вторых, происходит изменение состояния трущихся тел (нагревание, изменение агрегатного состояния и т.д.).
Такие изменения состояния тел сопровождаются изменением запаса их энергии. Энергию, зависящую от состояния тела, в частности, от его температуры, называют внутренней энергией.
Внутренняя энергия тела может изменяться при совершении работы тела или над телом, а также при передаче теплоты от одного тела к другому. Внутренняя энергия измеряется в тех же единицах, что и механическая.
Если рассматривать все тела, участвующие в процессе, и учитывать изменение и механической и внутренней энергии всех тел, то в итоге получим, что полная энергия — величина постоянная. Это закон сохранения полной энергии. В термодинамике он носит название первого начала и формулируется следующим образом: теплота, сообщенная газу, идет на изменение его внутренней энергии и на работу, совершаемую газом против внешних сил:
Процесс, при котором передача теплоты настолько ничтожна, что ей можно пренебречь, называется адиабатическим.
Передача теплоты — процесс, при котором внутренняя энергия одного тела увеличивается, а другого, соответственно, уменьшается. Для характеристики этого процесса вводится понятие количества теплоты — это изменение внутренней энергии тела, происходящее при теплопередаче. При таком процессе Q=0, A=-DU, т.е. работа совершается газом за счет за счет изменения внутренней энергии.
Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что невозможно всю внутреннюю энергию системы превратить в полезную работу. Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.
Источник
Источник
