Давление льда на сосуд

Источник

Черноуцан А. И. О ледниках, скороварках и теореме Карно //Квант. – 1991. – № 3. – С. 39,42-44.

По специальной договоренности с редколлегией и редакцией журнала “Квант”

Если спросить у школьника, почему в морозный день коньки хорошо скользят по льду, то скорее всего можно услышать простой и очевидный ответ: «Конек трется о лед, между ними образуется тонкая водяная смазка, она и обеспечивает скольжение». Однако школьнику, более искушенному в физике, такой ответ покажется слишком простым и потому неинтересным. «Нет,- скажет он,- дело здесь не в трении, а в давлении конька на лед. При повышении давления температура плавления льда становится меньше 0 °С, а лед под коньком тает.» Что же, в принципе и такой ответ имеет право на существование – температура плавления льда действительно понижается при увеличении внешнего давления. Но физика – наука количественная, и поэтому, чтобы выяснить, имеет ли это физическое явление какое-нибудь отношение к катанию на коньках, необходимо сделать численные оценки.

Прежде всего обсудим, что такое температура плавления (или точка таяния) льда, чем она интересна. Как известно, при достижении этой температуры лед перестает нагреваться, и поглощаемое им тепло целиком идет на таяние льда. Если же тепло перестанет поступать, оставшийся лед и вода будут находиться в тепловом равновесии. Таким образом, температура плавления – это температура равновесия между водой и льдом при данном давлении. Так, при давлении 1 атм она равна 0 °С. А на сколько изменится эта температура при увеличении давления до 1,01 атм?

Оказывается, рассчитать смещение точки плавления льда нам поможет… теорема Карно. Да, да, та самая теорема, в которой идет речь о максимальном КПД тепловых машин. «При чем же здесь точка плавления льда?» – спросите вы. Дело в том, что Карно доказал теорему о максимальном КПД циклической тепловой машины любого типа, независимо от того, что в нее заложено в качестве рабочего тела: идеальный газ, тающий лед или мыльная пленка. Необходимо соблюсти лишь одно условие: машина должна получать тепло только при температуре T1, а отдавать – только при температуре T2 (на промежуточных этапах теплообмен не должен происходить). Максимальный КПД такой машины (ее называют идеальной машиной Карно) реализуется при медленном, обратимом режиме ее работы и, независимо от рабочего вещества машины, равен

(~eta = frac{A}{Q_1} = frac{T_1 – T_2}{T_1}) , (1)

где А – работа машины за цикл, Q1 – количество теплоты, полученное машиной от нагревателя.

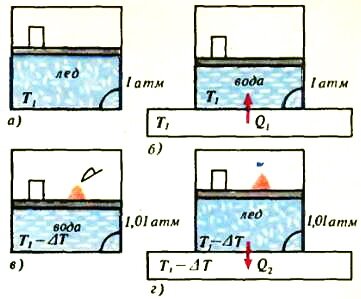
Рис. 1

Давайте представим нашу воображаемую машину Карно в виде цилиндра с поршнем (рис. 1, а). Заложим в нее лед массой m под давлением p1 = 1 атм при температуре t1 = 0 °C (T1 = 273 К). Постоянное давление будем обеспечивать грузом, лежащим на поршне. Чтобы подчеркнуть, что вода и лед находятся в равновесии, в уголке сосуда мы изобразили небольшое количество воды.

Опишем по этапам, как будет происходить один цикл в нашей машине Карно.

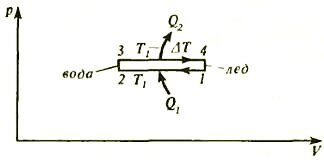
Рис. 2

1. Поставим цилиндр на нагреватель (термостат), имеющий температуру T1, и передадим системе количество теплоты Q1= λm, необходимое для плавления всего льда (λ – удельная теплота плавления). При этом поршень с грузом немного опустится (рис. 1, б), так как объем льда (~V_l = frac{m}{rho_l}) больше, чем объем воды (~V_v = frac{m}{rho_v}). На графике в координатах р, V (рис. 2) этому процессу соответствует линия 1-2.
2. Снимем сосуд с термостата и теплоизолируем его (рис. 1, в), после чего будем медленно увеличивать давление до тех пор, пока оно не станет равным p1 + Δp = 1,01 атм (для этого будем потихоньку подсыпать на поршень песочек). При этом температура системы понизится до значения T2 = T1 – ΔT, равного температуре плавления льда при давлении 1,01 атм.
3. Поставим сосуд на термостат с температурой T2 и будем отбирать тепло до тех пор, пока вся вода снова не замерзнет (рис. 1, г). На графике (см. рис. 2) этому процессу соответствует линия 3-4.
4. Осталось только теплоизолировать сосуд и медленно снять с поршня весь песок – и мы вернемся к начальному состоянию.

Теперь проведем расчеты. Работу за цикл легко найти из графика в координатах р, V – она равна площади фигуры, ограниченной графиком:

(~A = Delta p(V_l – V_v) = Delta p left(frac{m}{rho_l} – frac{m}{rho_v} right)) .

Количество теплоты, полученное от нагревателя, равно

(~Q_1 = lambda m) .

Поэтому из теоремы Карно (1) получаем

(~frac{Delta p left(frac{m}{rho_l} – frac{m}{rho_v} right)}{lambda m} = frac{Delta T}{T_1}) ,

или, для любой температуры T1 = Т,

(~Delta T = Delta p frac{T}{lambda} left(frac{1}{rho_l} – frac{1}{rho_v} right)) . (2)

Это соотношение называют уравнением Клапейрона – Клаузиуса. Подставив в него численные значения, получим, что при Δp = 0,01 атм ΔT = 9,2·10-5 К. Видно, что эффект очень слабый. Для изменения температуры плавления на 1 К, например, придется создать давление ≈ 133 атм. Вернемся, однако, к нашим конькам.

Давление человека в коньках можно оценить как (~p = frac{mg}{S})≈ 600 Н / 2 см2 = 30 атм. Тогда смещение точки плавления под коньками составит «0,3 К, что, конечно, очень мало в морозный день. Так что прав оказался «наивный» школьник: смазка образуется в первую очередь за счет трения. А какова же в таком случае роль коньков? Ведь они все-таки нужны! Не обсуждая подробно «физику катания», отметим один очевидный факт: для смазки поверхности конька, площадь которой мала, нужно растопить гораздо меньше льда, чем для смазки подошвы ботинка.

Встречаются ли в окружающей нас действительности такие давления, при которых происходит заметное смещение точки плавления льда? Безусловно, встречаются. Приведем лишь один пример – преодоление препятствий сползающим по склону тяжелым ледником. В том месте, где ледник упирается в кусок скалы или камень, создается очень большое давление, и лед начинает подтаивать. Ледник как бы оплывает камень в своем движении, пропуская его сквозь себя. После «снятия» давления вода на леднике снова замерзает.

«Это, конечно, интересно, но уж очень экзотично,- скажете вы.- Неужели это все, чего мы достигли?» Нет, конечно. Посмотрим внимательно на наш результат. Мы научились вычислять, как меняется температура равновесия двух фаз – жидкость (вода) и твердое тело (лед) – при изменении внешнего давления. Самое замечательное то, что вместо этих фаз можно взять любые другие, лишь бы они находились в тепловом равновесии друг с другом. Например, жидкость – пар, металл – расплав, твердое тело – пар и т. д. Другими словами, уравнение Клапейрона – Клаузиуса справедливо не только для плавления, но и для любого другого процесса перехода вещества из одной фазы в другую (испарение, сублимация и пр.). В формулу (2) тогда войдут плотности вещества в этих фазах и соответствующая удельная теплота фазового превращения.

В качестве примера рассмотрим переход вода – пар.

Как вы знаете, пар, находящийся в равновесии с водой, называют насыщенным. Зависимость между температурой насыщенного пара и его давлением используется для расчета влажности воздуха, определения точки росы и т. д. Кроме всего прочего, температура насыщенного пара (температура равновесия вода – пар) определяет точку кипения воды при данном внешнем давлении. Так, при давлении 1 атм температура кипения равна 100 С (373 К). С другой стороны, хорошо известно, что давление насыщенного пара растет при увеличении температуры. На этом свойстве – росте температуры кипения с давлением основан, в частности, принцип работы скороварки, где продукты готовятся при большем давлении и большей температуре.

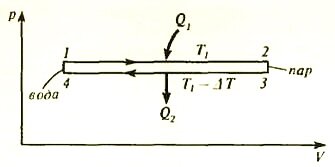
Рис. 3

В чем же различие между процессами таяния льда и испарения воды? Почему в одном случае температура равновесия фаз с ростом давления уменьшается, а в другом увеличивается? Дело вот в чем. Когда лед поглощает тепло и плавится, объем системы уменьшается (плотность воды больше плотности льда), а когда вода поглощает тепло и испаряется, объем системы увеличивается (плотность насыщенного пара меньше плотности воды). Однако график цикла в координатах р, V и в том, и в другом случае должен идти по часовой стрелке – иначе работа машины за цикл будет отрицательной. Сравните ход обоих графиков (см. рис. 2 и 3) и вы поймете, почему в одном случае большему давлению соответствует меньшая температура, а в другом – наоборот. Попробуйте, кроме того, продумать последовательность действий, которые надо совершить с сосудом, содержащим воду и пар, чтобы получился изображенный на графике цикл Карно.

Мы же завершим наш рассказ численной оценкой смещения точки кипения при увеличении давления от 1 атм до 1,01 атм. Для этого в формуле (2) заменим удельную теплоту плавления льда на удельную теплоту парообразования воды r, а плотность льда – на плотность насыщенного пара ρp:

(~Delta T = Delta p frac{T}{r} left(frac{1}{rho_p} – frac{1}{rho_v} right)) .

Плотность насыщенного водяного пара при Т = 373 К и р = 1 атм найдем из уравнения Менделеева – Клапейрона:

(~rho_p = frac{pM}{RT}) ≈ 0,58 кг/м3.

Подставляя численные значения, для Δp = 0,01 атм получаем ΔT ≈ 0,28 К. Как видите, в этом случае эффект довольно заметный: чтобы увеличить температуру кипения на 1 К, надо поднять давление всего на 0,035 атм, что вполне реально даже при обычных условиях.

Источник

    Поместим чашку со льдом и сосуд с разбавленным водным раствором соли под стеклянный колокол (рис. 81). При постоянной температуре ниже 0°С откачаем из колокола воздух. Вода будет испаряться как из раствора, так и из льда, пока не будет достигнута концентрация водяного пара, отвечающая равновесию, т. е. давлению насыщенного пара. Так как был взят разбавленный раствор произвольной концентрации, то чрезвычайно мало вероятно, чтобы при данной температуре давление насыщенного пара над ним случайно оказалось равным давлению пара над льдом. Поэтому допустим, как бол ее общий случай, что давления различны. Пусть насыщенный водяной пар над раствором обладает меньшим давлением, чем над льдом. Тогда пар, насыщенный по отношению к льду, будет пересыщенным в отношении к раствору и будет частично конденсироваться в нем. В результате понижения концентрации пара он окажется ненасыщенным в отношении льда, и некоторое количество последнего вновь испарится, доводя пар до насыщения в отношении льда. Пар, вновь сделавшись пересыщенным в отношении раствора, опять частично в нем сконденсируется. [c.243]

    Этим двум степеням свободы отвечают температура и давление, поэтому рассмотрим Р-Т-диаграмму воды (рис. IV. 1). Линия ОК – зависимость температуры кипения воды от давления (давления насыщенного пара над водой – от температуры). Линия ОВ – зависимость температуры таяния льда от давления (давления системы-от температуры). Линия О А-зависимость температуры сублимации льда от давления (давления пара над льдом – от температуры). Тогда часть диаграммы между линиями [c.193]

    В точке О кривая давления пара над жидкой водой пересекается с кривой давления пара над льдом. Этой точке отвечает равновесное существование всех трех фаз  [c.69]

    Обычно зависимость равновесий от этих параметров выражают графически. На рис. VH.l показана простейшая диаграмма состояния системы, состоящей из одного вещества – воды. Линия ОВ выражает зависимость давления насыщенного пара жидкой воды от температуры. Линия АО дает такую же зависимость для давления пара надо льдом. Точка О, в которой пересекаются эти линии, есть температура замерзания, как отмечалось в гл. [c.84]

    Очевидно, что давление пара над переохлажденной жидкостью. .. равновесного давления пара над льдом, выраженного кривой возгонки В А (рис. 5.7). В этом случае как и во всех других, давление пара над метастабильной фазой выше, чем над. .., если сопоставляемые фазы находятся при одинаковой. … [c.264]

    Кривая АО характеризует изменение давления пара над льдом с ростом температуры (лед пар Ф = 2, С=1). Из положения этой линии на диаграмме следует, что давление пара над льдом мало и растет с повышением температуры. Прн температуре, соответствующей точке О, лед плавится и превращается в жидкую воду. [c.183]

    Например, пар в указанной выше области молсет существовать при самых различных сочетаниях р и Г. Если, однако, эти параметры изменить так, чтобы появилась жидкость или твердая фаза, например, повысив давление или понизив температуру, то установится равновесие между двумя фазами (жидкость – нар или нар – твердая фаза). При этом новом условии параметры р и Т уже нельзя произвольно менять – определенному значению одного из них соответствует определенное значение другого. Эта связь для равновесия жидкость – нар выражается линией 08, разделяющей области существования этих фаз. Линия ОВ также дает зависимость давления насыщенного пара от температуры, описываемую уравнением Клапейрона – Клаузиуса (см. гл. II). Граница между твердой и газовой фазами определяется линией АО, которая передает зависимость давления пара надо льдом. Линия ОС показывает зависимость температуры плавления льда от давления. Таким образом, три линии на рис. У.1 соответствуют двухфазным равновесиям и выражают для них связь между р и Т. [c.77]

    Давление пара надо льдом [c.42]

    Примечание Р-давление пара надо льдом [c.668]

    Как видно из диаграмм, давление паров воды над водными растворами-хлористого кальция и хлористого лития всегда меньше давления паров надо льдом при равных температурах. Гомогенные растворы указанных солей обеспечивают депрессию давления паров воды по сравнению с упругостью паров надо льдом. [c.281]

    Содержащийся в воздухе водяной пар также активно участвует в тепловом балансе земной поверхности. Он (как и углекислый газ) пропускает большую часть солнечных лучей и в значительной степени задерживает обратное тепловое излучение земли, таким образом способствуя сохранению ею тепла. Как известно, испаряется не только вода, но и лед, однако при низких температурах давление пара надо льдом весьма мало  [c.10]

    Активность вещества в системе, находящейся в состоянии равновесия, имеет одно и то же значение для каждой фазы в системе, в которой это вещество является одним из компонентов. Так, в системе лед – вода – пары воды при 0° активность воды имеет одно значение для всех трех фаз. Обычно активность выражают через парциальное давление или концетрацию в данном случае давление пара над льдом и давление пара над жидкостью равны парциальному давлению паров воды в газовой фазе. Если бы присутствовало некоторое количество эфира, образующего другую жидкую фазу, то количество воды, растворенной в эфире, отвечало бы условию равенства парциального давления воды для смеси эфира с водой и для других фаз. [c.344]

    Обратимся к явлениям замерзания растворов. Здесь также полезно вспомнить диаграмму состояния воды, изображенную на рис. 22. Напомним, что жидкая вода, лед и пар могут сосуществовать только тогда, когда давление пара над жидкой водой равно давлению пара над льдом. Это же условие справедливо для любого чистого вещества и для раствора. [c.107]

    Равновесное давление пара над льдом при – 10°С равно 1,950 мм, а над переохлажденной водой при той же температуре 2,149 мм. Вычислите ДО и Д5 перехода 1 моля переохлажденной воды в лед при -10 °С и постоянном обшем давлении. (ДО -40 кал.) [c.383]

    Измерение влажности психрометрическим методом при низких температурах требует повышенной точности определения психрометрической разности, так как даже небольшая погрешность приводит к серьезным ошибкам в величине влажности. Так, при температуре -10° С погрешность в измерении психрометрической разности в 0,2° влечет за собой ошибку в величине относительной влажности на 5%. Кроме того, при отрицательных температурах вода на мокром термометре замерзает. Это не препятствует измерению психрометром как местным прибором, поскольку в расчет может быть принято давление пара над льдом. Для дистанционного измерения замерзание воды создает большие трудности, так как практически невозможно постоянно обновлять слой льда на мокром термометре. В связи с этим психрометрический метод дистанционного измерения влажности находит применение лишь при положительных температурах. [c.241]

    Давление пара растворителя над раствором становится равным давлению пара над льдом в точке В, т. е. при более низкой температуре, чем Го, и температура отвечает точке замерзания данного раствора. Из рисунка 24 видно, что всегда Г3. понижение температуры замерзания АГ3. = Го – Г3. растет с концентрацией, вместе с увеличением расстояния между кривыми I и И, или [c.103]

    Кривая АО характеризует изменение давления пара над льдом с ростом температуры (равновесие лед пар Ф=2, С = 1). Из положения этой линии на диаграмме следует, что давление пара над льдом мало и растет с повышением температуры. При температуре, соответствующей точке О, лед плавится и превращается в жидкую воду. Кривая ОС выражает уже зависимость изменения давления насыщенного пара над жидкой водой с ростом температуры (равновесие вода пар Ф=2, С = 1). [c.166]

    К и 0,006 атм (4,58 мм рт. ст.) соответствуют единственным условиям сосуществования воды во всех трех агрегатных состояниях – жидком, твердом и парообразном. Температура 273,16 К – температура плавления льда при давлении насыщенного пара воды. Эта точка выше нуля Цельсия. За нуль же температуры принимается по шкале Цельсия, как известно, точка плавления при давлении 1 атм. Заканчивается рассматриваемая кривая при давлении около 2100 атм и температуре около-20°С, что является наиболее низкой температурой плавления обычного льда. При давлениях выше 2100 атм обычный лед (лед I) начинает переходить в иную кристаллическую модификацию воды – так называемый лед III. Подробнее об этом несколько позже (см. рис. 51). Кривая ОВ выражает зависимость давления насыщенного пара жидкой воды от температуры. Она начинается в тройной и заканчивается в критической точке (374°С и 220 атм). Однако при осторожном охлаждении чистой воды ее можно получить в переохлажденном состоянии. Прерывистая кривая 0D отвечает давлению пара над такой переохлажденной метастабильной водой, т. е. водой, находящейся в неустойчивом состоянии. Эта кривая расположена выше кривой АО, выражающей зависимость давления пара над льдом. В этой области (т. е. левее точки О) жидкая вода должна самопроизвольно переходить в твердое состояние и переход будет связан с убылью энергии Г иббса. Кривую Л О не удается продлить в неустойчивую область правее точки О, т. е. перегреть твердое вещество выше точки плавления нельзя. Таким образом, кривая А О заканчивается в тройной точке. Начинается же она, как можно считать, при абсолютном нуле. [c.124]

    Представим графически результаты, содержащиеся в табл. 13 и 14 (рис. 24). Зависимость давления пара над жидкостью не является прямолинейной (рис. 24). Судить о характере зависимости давления пара над льдом невозможно, так ак кривая почти сливается с осью температуры. Можно, конечно, растянуть ось давления пара, но тогда все точки не поместятся на одном графике. [c.106]

    Порядок обработки данных для давления пара над льдом представлен в табл.15. [c.107]

    Уравнение у = а + Ьх приобретает вид для зависимости давления пара над льдом [c.107]

    Предположим, температура плавления неизвестна. При температуре плавления Гпл сосуществуют три равновесные фазы жидкость, лед и пар, причем давление пара над льдом при Гдл равно давлению пара над жидкостью. Объединяя уравнения I и II, вычисляем Гдл [c.109]

    Давление паров надо льдом и над переохлажденной водой при той же температуре неодинаково  [c.137]

    При 0° С давление пара надо льдом равно давлению пара над водой – вода и лед находятся в динамическом равновесии. Согласно принципу Ле-Шателье (см. стр. 181), с увеличением давления это равновесие сдвинется влево, а с уменьшением – вправо. Опыт подтверждает это положение, так как при увеличении давления температура плавления льда понижается. Например, при увеличении давления на каждые 130 атм температура замерзания воды снижается примерно на 1° С. Однако при давлении выше 2000 атм температура плавления льда повышается. Так, лед, образованный при 20 766 атм, тает при +76° С и поэтому называется горячим, [c.137]

    Опыт показывает, что разбавленный раствор замерзает при температуре более низкой, чем чистый растворитель. Это также связано с понижением давления пара над раствором. Поясним эту связь рис. 43, на котором кривая О А характеризует давление пара над чистым жидким растворителем, ВС – над раствором неэлектролита и DE – давление пара над раствором электролита. FG – давление пара над раствором электролита с большей концентрацией. НО – давление пара над растворителем в твердом состоянии. При температуре замерзания лед находится в равновесии с жидкостью и поэтому давление пара над обеими фазами одинаково. Отсюда следует, что температуры замерзания T a растворителя, Т – раствора неэлектролита и T a – раствора электролита, отвечают точкам пересечения О, В я D кривых давления пара над ними с кривой давления пара над льдом. Как следует из рисунка, понижение температуры замерзания АТ = Тз – Т связано с понижением давления пара и зависит от концентрации растворенного ве-ш,ества. [c.151]

    Так как при замерзании вода увеличивается в объеме, то повышение давления, в соответствии с принципом смещения равновесий (стр. 170), способствует плавлению льда и понижает температуру замерзания воды. В точке О кривая давления пара над жидкой водой пересекается с кривой давления пара над льдом и с кривой точек замерзания. Этой особой точке отвечает равновесное существование всех трех фаз лед вода ii пар. Для такой системы правило фаз дает число степеней свободы, разное нулю. Точка, отвечающая равновесию трех фаз, называется тройной точкой. В соответствии с правилом фаз равновесие в системе лед = вода пар возможно только при строго определенных условиях, именно, при давлении 4,579 мм рт. ст. и техмпературе 0,0098° С .  [c.196]

    Порядок обработки данных для давления пара надо льдом представлен в табл. 8. [c.71]

    Так как давление пара над льдом меньше, чем над водой, то водяной пар из клеток постепенно диффундирует через оболочку в межклеточное пространство. Поэтому чем интенсивнее и быстрее протекает процесс замораживания, тем меньше влаги переходит из клеток в межклеточное пространство и тем в большем количестве она замерзает внутри волокон, образуя мелкие кристаллы льда. И, наоборот, чем температура выше и скорость замораживания меньше, тем больше влаги выделяется [c.8]

    На рис. II представлена Р(Т )-диаграмма для НгО в тройной точке. Согласно Васбурну (Дорсей, 1940) давление пара над льдом ] описывается соотношением [c.43]

    Илфельд [87] показал, что при переводе температур точки росы в единицы действительной влажности в газах требуется определенная осторожность. Выше О °С расчеты содержания влаги, основанные на измерении давления пара над водой, находятся в хорошем согласии с экспериментом. Согласно теории, для расчета содержания влаги в газе при температурах ниже точки замерзания воды следует использовать давление пара надо льдом. В действительности, однако, экстраполирование давления пара над водой дает более правильные результаты, чем другие методы. Ил- [c.570]

    Так как при замерзании вода увеличивается в объеме, то повышение давления, в соответствии с принципом смещения равновесий (стр. 16 ). способствует плавлению льда и понижает температуру замерзания воды. В точке О кривая давления пара над жидкой водой пересекается с кривой давления пара над льдом и с кривой точек замерзания. Этой особой точке отвечает равновесное существование всех трех фаз лед водапар. [c.186]

Краткий справочник химика Издание 6 (1963) — [ c.359 ]

Краткий справочник химика Издание 4 (1955) — [ c.309 ]

Краткий справочник химика Издание 7 (1964) — [ c.359 ]

Источник