Давление на вертикальную стенку сосуда водой

4.2. Элементы гидростатики
4.2.3. Гидростатическое давление
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление.
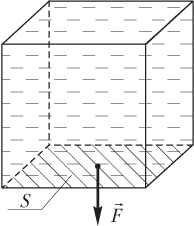
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
pгидр = ρ0gh,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
Fгидр = pгидрS = ρ0ghS,
где pгидр — гидростатическое давление на дно сосуда; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь дна сосуда.
Рис. 4.10
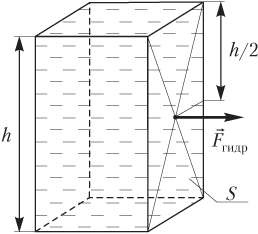
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
pгидр=ρ0gh2,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
Рис. 4.11
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
Fгидр=pгидрS=ρ0gh2S,
где pгидр — гидростатическое давление на дно сосуда; ρж — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь вертикальной стенки.
Рис. 4.11
При расчете давленияна днооткрытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — глубина водоема.
Рис. 4.12
Сила давления на дно открытого водоема определяется произведением:
F = pS = (pатм + ρ0gh)S,
где S — площадь дна водоема.
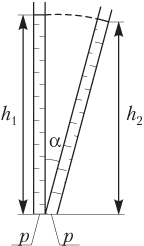
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
p = ρ0gh1 cos α,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h1 — высота столба жидкости при вертикальном положении мензурки; h2 = h1 cos α — высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Рис. 4.13
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см3. Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение. Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
〈Fгидр〉=〈p〉S,
где 〈p〉 — среднее гидростатическое давление на боковую поверхность цилиндра; S — площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
〈p〉=ρ0gh2,
где ρ0 — плотность жидкости, заполняющей сосуд; g — модуль ускорения свободного падения; h — высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
S = 2πRh,
где 2πr — длина окружности; R — радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая — периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления 〈p〉 и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
〈Fгидр〉=πρ0gRh2.
Расчет дает значение:
〈Fгидр〉=π⋅2,5⋅103⋅10⋅10⋅10−2⋅(30⋅10−2)2≈707 Н≈0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см3. Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение. Давление в открытом водоеме определяется формулой
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — искомая глубина водоема.
По условию задачи
p = 4pатм.
Подстановка указанного значения в исходную формулу дает:
4pатм = pатм + ρ0gh,
или
3pатм = ρ0gh.
Выразим отсюда искомую глубину водоема
h=3pатмρ0g
и произведем вычисление:
h=3⋅100⋅1031,0⋅103⋅10=30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.
Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòàòè÷åñêèì.
Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:
1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:
2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
F=mg. (1.28)
Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:
m = pV, (1.29)
à îáúåì — ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:
V=Sh. (1.30)
Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:
F = pVg=pShg. (1.31)
Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:
pS = pSkg.
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:
p = phg.
Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.
Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàêæå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ — ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.
 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.
Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæàþùèõñÿ — áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñóäîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S — ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ — ñïîñîáíîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.
Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëåíèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâøèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëåíèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Источник
Физика
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление .
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
где ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
F гидр = p гидр S = ρ 0 ghS ,
где p гидр — гидростатическое давление на дно сосуда; ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь дна сосуда.
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
где ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
F гидр = p гидр S = ρ 0 g h 2 S ,
где p гидр — гидростатическое давление на дно сосуда; ρ ж — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь вертикальной стенки.
При расчете давления на дно открытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
где p атм — атмосферное давление; ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h — глубина водоема.
Сила давления на дно открытого водоема определяется произведением:
F = pS = ( p атм + ρ 0 gh ) S ,
где S — площадь дна водоема.
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
где ρ 0 — плотность жидкости; g — модуль ускорения свободного падения; h 1 — высота столба жидкости при вертикальном положении мензурки; h 2 = h 1 cos α — высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см 3 . Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение . Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
где 〈 p 〉 — среднее гидростатическое давление на боковую поверхность цилиндра; S — площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
где ρ 0 — плотность жидкости, заполняющей сосуд; g — модуль ускорения свободного падения; h — высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
где 2π r — длина окружности; R — радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая — периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления 〈 p 〉 и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
〈 F гидр 〉 = π ρ 0 g R h 2 .
Расчет дает значение:
〈 F гидр 〉 = π ⋅ 2,5 ⋅ 10 3 ⋅ 10 ⋅ 10 ⋅ 10 − 2 ⋅ ( 30 ⋅ 10 − 2 ) 2 ≈ 707 Н ≈ 0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см 3 . Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение . Давление в открытом водоеме определяется формулой
где p атм — атмосферное давление; ρ 0 — плотность воды; g — модуль ускорения свободного падения; h — искомая глубина водоема.
Подстановка указанного значения в исходную формулу дает:
4 p атм = p атм + ρ 0 gh ,
Выразим отсюда искомую глубину водоема
и произведем вычисление:
h = 3 ⋅ 100 ⋅ 10 3 1,0 ⋅ 10 3 ⋅ 10 = 30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
Гидростатический парадокс или парадокс Паскаля
Гидростатический парадокс или парадокс Паскаля — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равна весу жидкости лишь для сосуда цилиндрической формы. Математическое объяснение парадоксу было дано Симоном Стевином в 1612 году.
Причины
Причина гидростатического парадокса состоит в том, что по закону Паскаля жидкость давит не только на дно, но и на стенки сосуда.
Если стенки сосуда вертикальные, то силы давления жидкости на его стенки направлены горизонтально и не имеют вертикальной составляющей. Сила давления жидкости на дно сосуда в этом случае равна весу жидкости в сосуде. Если же сосуд имеет наклонные стенки, давление жидкости на них имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда, поэтому он и отличается от давления на дно.
Опыт Паскаля
В 1648 году парадокс продемонстрировал Блез Паскаль . Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
Гидростатический парадокс и закон Архимеда
Похожий кажущийся парадокс возникает при рассмотрении закона Архимеда . Согласно распространённой формулировке закона Архимеда , на погружённое в воду тело действует выталкивающая сила, равная весу воды, вытесненной этим телом. Из такой формулировки можно сделать неверное умозаключение, что тело не сможет плавать в сосуде, не содержащем достаточное количество воды для вытеснения.
Однако на практике тело может плавать в резервуаре с таким количеством воды, масса которой меньше массы плавающего тела. Это возможно в ситуации, когда резервуар лишь ненамного превышает размеры тела. Например, когда корабль стоит в тесном доке, он остаётся на плаву точно так же, как в открытом океане, хотя масса воды между кораблём и стенками дока может быть меньше, чем масса корабля.
Объяснение парадокса заключается в том, что архимедова сила создаётся гидростатическим давлением, которое зависит не от веса воды, а только от высоты её столба. Как в гидростатическом парадоксе на дно сосуда действует сила весового давления воды, которая может быть больше веса самой воды в сосуде, так и в вышеописанной ситуации давление воды на днище корабля может создавать выталкивающую силу, превышающую вес этой воды.
Более корректной формулировкой закона Архимеда является следующая: на погружённое в воду тело действует выталкивающая сила, эквивалентная весу воды в погружённом объёме тела.
Источник
Давление на вертикальную стенку сосуда водой
Возьмем цилиндрический сосуд с горизонтальным дном и вертикальными стенками, наполненный жидкостью до высоты
(рис. 248).
Рис. 248. В сосуде с вертикальными стенками сила давления на дно равна весу всей налитой жидкости
Рис. 249. Во всех изображенных сосудах сила давления на дно одинакова. В первых двух сосудах она больше веса налитой жидкости, в двух других — меньше
Гидростатическое давление в каждой точке дна сосуда будет одно и то же:
.
Если дно сосуда имеет площадь
, то сила давления жидкости на дно сосуда , т. е. равна весу жидкости, налитой в сосуд.
Рассмотрим теперь сосуды, отличающиеся по форме, но с одинаковой площадью дна (рис. 249). Если жидкость в каждом из них налита до одной и той же высоты
, то давление на дно . во всех сосудах одно и то же. Следовательно, сила давления на дно, равная
,
также одинакова во всех сосудах. Она равна весу столба жидкости с основанием, равным площади дна сосуда, и высотой, равной высоте налитой жидкости. На рис. 249 этот столб показан около каждого сосуда штриховыми линиями. Обратите внимание на то, что сила давления на дно не зависит от формы сосуда и может быть как больше, так и меньше веса налитой жидкости.
Рис. 250. Прибор Паскаля с набором сосудов. Сечения
одинаковы у всех сосудов
Рис. 251. Опыт с бочкой Паскаля
Этот вывод можно проверить на опыте при помощи прибора, предложенного Паскалем (рис. 250). На подставке можно закреплять сосуды различной формы, не имеющие дна. Вместо дна снизу к сосуду плотно прижимается подвешенная к коромыслу весов пластинка. При наличии жидкости в сосуде на пластинку действует сила давления, которая отрывает пластинку, когда сила давления начнет превосходить вес гири, стоящей на другой чашке весов.
У сосуда с вертикальными стенками (цилиндрический сосуд) дно открывается, когда вес налитой жидкости достигает веса гири. У сосудов другой формы дно открывается при той же самой высоте столба жидкости, хотя вес налитой воды может быть и больше (расширяющийся кверху сосуд), и меньше (суживающийся сосуд) веса гири.
Этот опыт приводит к мысли, что при надлежащей форме сосуда можно с помощью небольшого количества воды получить огромные силы давления на дно. Паскаль присоединил к плотно законопаченной бочке, налитой водой, длинную тонкую вертикальную трубку (рис. 251). Когда трубку заполняют водой, сила гидростатического давления на дно становится равной весу столба воды, площадь основания которого равна площади дна бочки, а высота равна высоте трубки. Соответственно увеличиваются и силы давления на стенки и верхнее днище бочки. Когда Паскаль заполнил трубку до высоты в несколько метров, для чего потребовалось лишь несколько кружек воды, возникшие силы давления разорвали бочку.
Как объяснить, что сила давления на дно сосуда может быть, в зависимости от формы сосуда, больше или меньше веса жидкости, содержащейся в сосуде? Ведь сила, действующая со стороны сосуда на жидкость, должна уравновешивать вес жидкости. Дело в том, что на жидкость в сосуде действует не только дно, но и стенки сосуда. В расширяющемся кверху сосуде силы, с которыми стенки действуют на жидкость, имеют составляющие, направленные вверх: таким образом, часть веса жидкости уравновешивается силами давления стенок и только часть должна быть уравновешена силами давления со стороны дна. Наоборот, в суживающемся кверху сосуде дно действует на жидкость вверх, а стенки — вниз; поэтому сила давления на дно оказывается больше веса жидкости. Сумма же сил, действующих на жидкость со стороны дна сосуда и его стенок, всегда равна весу жидкости. Рис. 252 наглядно показывает распределение сил, действующих со стороны стенок на жидкость в сосудах различной формы.
Рис. 252. Силы, действующие на жидкость со стороны стенок в сосудах различной формы
Рис. 253. При наливании воды в воронку цилиндр поднимается вверх.
В суживающемся кверху сосуде со стороны жидкости на стенки действует сила, направленная вверх. Если стенки такого сосуда сделать подвижными, то жидкость поднимет их. Такой опыт можно произвести на следующем приборе: поршень неподвижно закреплен, и на него надет цилиндр, переходящий в вертикальную трубку (рис. 253). Когда пространство над поршнем заполняется водой, силы давления на участках
и стенок цилиндра поднимают цилиндр вверх.
Источник
Источник