Давление смеси газа в сосуде равно
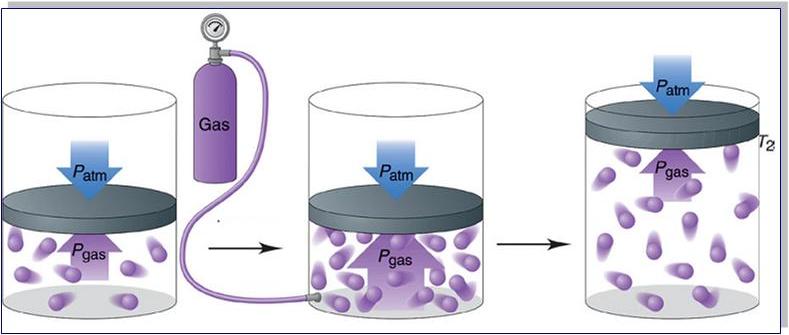
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия – упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах

Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
P = F/S
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
F*Δt = Δp
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 1023), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
P = N*m*v2/(3*V)
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
P*V = n*R*T
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
P = n*R*T/V
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
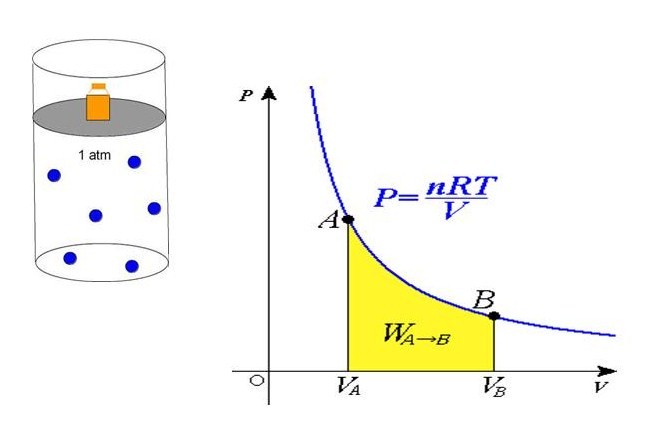
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
P = N*m*v2/(3*V)
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
m = M/NA;
n = N/NA;
m*N = M*n;
P = M*n*v2/(3*V)
Объем сосуда в кубических метрах равен 0,01 м3. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Источник
Парциальное давление и объем
Содержание:
Когда мы имеем дело со смесями газов, важно знать, что они имеют такие характеристики, как парциальный объем и парциальное давление. Для начала определим, что такое смесь идеальных газов.
Смесь идеальных газов – это смесь нескольких газообразных веществ, которые при заданных условиях не будут вступать в определенные химические реакции.
При смене условий (например, повышении температуры, понижении давления) газовая смесь все же может вступать во взаимодействие. Важный параметр любой такой смеси – так называемая весовая концентрация g i i -ного газа-компонента.
- N – количество газов, из которых состоит смесь;
- x i i -го газа – молярная концентрация указанного газа в составе смеси;
- ν i – количество молей i -го газа, присутствующего в смеси.
Понятие парциального давления
Парциальное давление – это особая характеристика, описывающая состояние компонентов смеси идеальных газов. Сформулируем основное определение:
Парциальным называется давление p i , которое могло бы создаваться i -ым газом в смеси при условии отсутствия остальных газов и сохранения исходного объема и температуры.
Формула парциального давления будет выглядеть так:
p i = m i μ i R T V = μ i R T V
Объем смеси здесь обозначен буквой V , ее температура – T .
Следует подчеркнуть, что поскольку средние кинетические энергии молекул смеси равны, то существует и равенство температур всех компонентов газовой смеси, находящейся в состоянии термодинамического равновесия.
Для нахождения давления смеси идеальных газов нужно воспользоваться законом Дальтона в следующей формулировке:
p = ∑ i = 1 N p i = R T V ∑ i = 1 N ν i
Исходя из него, мы можем выразить парциальное давление так:
Понятие парциального объема
У газовой смеси также есть такая характеристика, как парциальный объем.
Парциальный объем V i i -газа в газовой смеси – это такой объем, который мог бы иметь газ при условии отсутствия всех остальных газов и сохранении исходной температуры и объема.
Если речь идет о смеси идеальных газов, то к ней применим закон Амага:
В самом деле, при выражении ν i из формулы выше у нас получится следующее:
ν i = p V i R T ; p = R T V p R T ∑ i = 1 N V i → V = ∑ i = 1 N V i
Для расчета парциального объема газа используется следующая формула:
Нам известно, что параметры, определяющие состояние смеси идеальных газов, будут подчиняться уравнению Менделеева-Клайперона. Формула будет выглядеть так:
p V = m μ s m R T .
Все параметры данного уравнения будут относиться ко всей смеси. Это же уравнение удобнее записать так:
Здесь параметры R s m = R μ s m = R ∑ i = 1 N q i μ i означают удельную газовую постоянную смеси.
Условие: имеется сосуд объемом 1 м 3 , в котором находится 0 , 10 · 10 – 3 к г гелия и 0 , 5 · 10 – 3 к г водорода. Постоянная температура равна 290 К . Вычислите давление смеси и парциальное давление гелия в нем.
Начнем с вычисления количества молей каждого компонента смеси. Для этого можно использовать формулу:
Зная, что молярная масса водорода, согласно таблице Менделеева, составляет μ H 2 = 2 · 10 – 3 к г м о л ь , мы можем найти количество его молей в смеси по формуле:
ν H 2 = m H 2 μ H 2
Считаем, что получится:
ν H 2 = 0 , 5 · 10 – 3 2 · 10 – 3 = 0 , 25 ( м о л ь ) .
Точно такие же расчеты проводим и для гелия, зная, что μ H e = 4 · 10 – 3 к г м о л ь :
Теперь с помощью уравнения Менделеева-Клайперона можно найти парциальное давление каждого компонента:
Сначала рассчитаем давление водорода:
p H 2 V = ν H 2 R T → p H 2 = ν H 2 R T V
Парциальное давление будет равно:
p H 2 = 0 , 25 · 8 , 31 · 290 1 = 602 , 5 ( П а ) .
Теперь то же самое подсчитываем для гелия:
p H e = 0 , 025 · 8 , 31 · 290 1 = 60 , 25 ( П а ) .
Чтобы найти общее давление смеси газов, сложим сумму давлений ее составляющих:
p = p H 2 + p H e
Подставляем полученные ранее значения и находим нужный результат:
p = 602 , 5 + 60 , 25 = 662 , 75 ( П а ) .
Ответ: общее давление смеси составляет 662 , 75 П а , а парциальное давление гелия в смеси равно 60 , 25 П а .
Условие: дана смесь газов, состоящая из 1 к г углекислого газа и 0 , 5 к г O 2 . Если считать их идеальными, какой объем они будут занимать при давлении в 1 а т м ? Температура смеси равна 300 К .
Начнем с вычисления общей массы газовой смеси.
m = m O 2 + m C O 2
Значит, m = 1 + 0 , 5 = 1 , 5 .
Переходим к вычислению массовых компонентов смеси:
g O 2 = 0 , 5 1 , 5 = 0 , 33 ; g C O 2 = 1 1 , 5 = 0 , 67 .
Тогда газовая постоянная смеси будет равна:
R s m = R ∑ i = 1 N g i μ i
R s m = 8 , 31 0 , 33 32 · 10 – 3 + 0 , 67 46 · 10 – 3 = 200 Д ж к г К .
Объем смеси вычисляем с помощью уравнения Менделеева-Клайперона:
V s m = m s m R s m T s m p s m
Вспомнив, что по условию давление равно 1 а т м , что равно 10 5 П а , вычислим объем:
V s m = 1 , 5 · 200 · 300 10 5 = 0 , 9 м 3 .
Ответ: при указанных условиях смесь займет объем, равный 0 , 9 м 3 .
Источник
Давление газа на стенки сосуда. Закон Дальтона
Давление газа на стенки сосуда
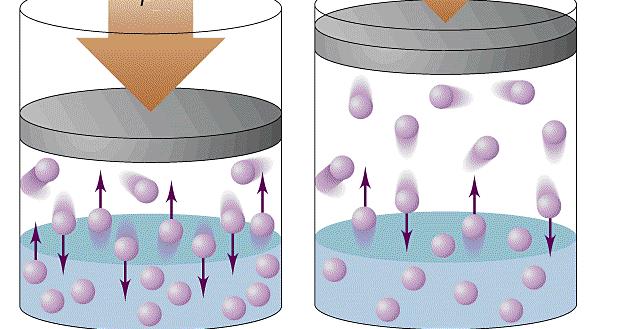
Вследствие теплового движения частицы газа время от времени ударяются о стенки сосуда (рис.1,а). При каждом ударе молекулы действуют на стенку сосуда с некоторой силой. Складываясь друг другом, силы ударов отдельных частиц, образуют некоторую силу давления, постоянно действующую на стенку сосуда. Молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда (рис.1,б).
Рис.1. Давление газа на стенку сосуда: а) возникновение давления вследствие ударов о стенку хаотически движущихся частиц; б) сила давления как результат упругого удара частиц.
На практике чаще всего имеют дело не с чистым газом, а со смесью газов. Например, атмосферный воздух представляет собой смесь азота, кислорода, углекислого газа, водорода и других газов. Каждый из газов, входящих в состав смеси, вносит свой вклад в суммарное давление, которое оказывает смесь газов на стенки сосуда.
Закон Дальтона для газовой смеси
Для газовой смеси справедлив закон Дальтона:
давление газовой смеси равно сумме парциальных давлений каждого компонента смеси:
Рис.2. Закон Дальтона для газовой смеси
С точки зрения молекулярно-кинетической теории закон Дальтона выполняется потому, что взаимодействие между молекулами идеального газа пренебрежимо мало. Поэтому каждый газ оказывает на стенку сосуда давление, как если бы остальных газов в сосуде не было.
Источник
Задачи на нахождение парциального давления газов и общего давления смеси
Задача 41.
Смешивают 0,04м 3 азота, находящегося под давлением 96кПа (720мм. рт. ст.), с 0,02м 3 кислорода. Общий объем смеси 0,06м 3 , а общее давление 97,6кПа (732мм. рт. ст.). Каким было давление взятого кислорода?
Решение:
По условию задачи объём азота увеличился в 1,5 раза (0,06/0,04 = 1,5), а объём кислорода – в 3 раза (0,06/0,02 = 3). Во столько же раз уменьшились парциальные давления газов.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь). Отсюда Исходя из того, что объём кислорода до смешения был в три раза больше, чем после смешения, рассчитаем давление кислорода до смешения:
Ответ: Робщ. = 100,8кПа.
Задача 42.
Газовая смесь приготовлена из 2л Н2 (Р = 93,3 кПа) и 5л CH4 (Р = 112 кПа). Объем смеси равен 7л. Найти парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём водорода увеличился в 3,5 раза (7/2 = 3,5), а объём метана – в 1,4 раза (7/5 = 1,4). Во столько же раз уменьшились парциальные давления газов.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Ответ:
Задача 43.
Газовая смесь состоит из NO и СО2. Вычислить объемное содержание газов в смеси (в %), если их парциальные давления равны соответственно 36,3 и 70,4 кПа (272 и 528мм. рт. ст.).
Решение:
Согласно закону Дальтона парциальное давление данного газа прямо пропорционально его мольной доли на общее давление смеси газов:
где Р(смеси) – общее давление смеси; Р(А) – парциальное давление данного газа;
(A) – мольная доля данного газа.
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Ответ: 34,02%NO; 65,98%CO.
Задача 44.
В закрытом сосуде вместимостью 0,6м 3 находится при 0 °С смесь, состоящая из 0,2кг СО2, 0,4кг 02 и 0,15кг СН4. Вычислить: а) общее давление смеси; б) парциальное давление каждого из газов; в) процентный состав смеси по объему.
Решение:
Вычислим общее количество газов в смеси по уравнению:
, где
– количество газа, кмоль; m – масса газа, кг; М – молекулярная масса газа, кг/моль. Тогда:
а) Общее давление смеси газов определяем по уравнению:
где Rk и
k , соответственно, парциальное давление, и количество газа в смеси.
Отношение парциальных (приведённых) объёмов отдельных газов к общему объёму смеси называется объёмной долей и определяется по формуле:
Ответ:
Задача 45.
Газовая смесь приготовлена из 0,03м 3 СН4, 0,04м 3 Н2 и 0,01м 3 СО. Исходные давления СН4, Н2 и СО составляли ответственно 96, 84 и 108,8 кПа (720, 630 и 816мм рт. ст.). Объем смеси равен 0,08м 3 . Определить парциальные давления газов и общее давление смеси.
Решение:
По условию задачи объём метана увеличился после смешения в 2,67 раза (0,08/0,03 = 2,67), объём водорода – в 2 раза (0,08/0,04 = 2), а объём угарного газа – в 8 раз (0,08/0,01 = 8). Во столько же раз уменьшились парциальные давления газов. Следовательно,
Согласно закону парциальных давлений, общее давление смеси газов, не вступающих во взаимодействие друг с другом, равно сумме парциальных давлений газов, составляющих систему (смесь).
Ответ:
Задача 46.
В газометре над водой находятся 7,4л кислорода при 23 °С и давлении 104,1 кПа (781 мм. рт. ст.). Давление насыщенного водяного пара при 23 °С равно 2,8 кПа (21мм. рт. ст.). Какой объем займет находящийся в газометре кислород при нормальных условиях?
Решение:
Парциальное давление кислорода равно разности общего давления и парциального давления паров воды:
Обозначив искомый объём через и, используя объединённое уравнение закона Бойля- Мариотта и Гей-Люссака, находим:
где Р и V – давление и объём газа при температуре Т = 296К (273 +23 = 296); Р = 101,325кПа; Т = 273К; Р = 104,1кПа; – объём газа при н.у.
Ответ: V =6,825л.
Источник
Источник
Прибор Рамзая для обнаружения парциального давления.
Во внутреннем сосуде Р из палладия находится смесь азота и водорода под общим давлением в 1 атм. Сосуд Р соединён с дифференциальным манометром и помещён в сосуд большего размера. При высоких температурах водород легко диффундирует через палладиевую оболочку, и стенки сосуда Р становятся полупроницаемыми – они проницаемы для водорода, но непроницаемы для азота. Пропуская нагретый водород с давлением в 1 атм через больший сосуд, исследователь обнаружит, что давление смеси газов в сосуде Р превысит 1 атм на величину парциального давления азота при данной температуре.
Парциа́льное давление (лат. partialis «частичный» от pars «часть») – давление, которое имел бы газ, входящий в состав газовой смеси, если бы он один занимал объём, равный объёму смеси при той же температуре[1][2][3]. Общее давление газовой смеси является суммой парциальных давлений её компонентов.
В химии парциальное давление газа в смеси газов определяется как указано выше. Парциальное давление газа, растворённого в жидкости, является парциальным давлением того газа, который образовался бы в фазе газообразования в состоянии равновесия с жидкостью при той же температуре. Парциальное давление газа измеряется как термодинамическая активность молекул газа. Газы всегда будут вытекать из области с высоким парциальным давлением в область с более низким давлением; и чем больше разница, тем быстрее будет поток. Газы растворяются, диффундируют и реагируют соответственно их парциальному давлению и не обязательно зависимы от концентрации в газовой смеси.
Законы Дальтона парциального давления[править | править код]
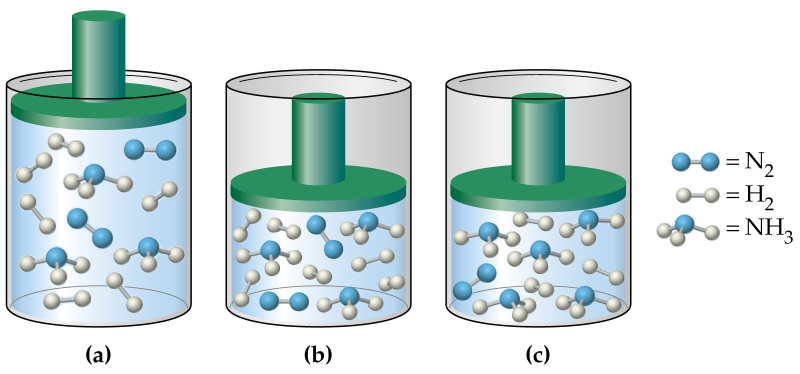
Для идеального газа парциальное давление в смеси равно давлению, которое будет оказываться, если бы он занимал тот же объём, что и вся смесь газов, при той же температуре. Причина этого в том, что между молекулами идеального газа по определению не действуют силы притяжения или отталкивания, их соударения между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. Насколько условия реально существующей смеси газов близки этому идеалу, настолько общее давление смеси равно сумме парциальных давлений каждого газа смеси, как это формулирует закон Дальтона[4]. Например, дана смесь идеального газа из азота (N2), водорода (H2) и аммиака (NH3):
, где:
= общему давлению в газовой смеси
= парциальному давлению азота (N2)
= парциальному давлению водорода (H2)
= парциальному давлению аммиака (NH3)
Смеси идеальных газов[править | править код]
Мольная доля отдельных компонентов газа в идеальной газовой смеси может быть выражена в пределах парциальных давлений компонентов или молей компонентов:
и парциальное давление отдельных компонентов газов в идеальном газе может быть получено используя следующее выражение:
, где:
= мольной доле любого отдельного компонента газа в газовой смеси
= парциальному давлению любого отдельного компонента газа в газовой смеси
= молям любого отдельного компонента газа в газовой смеси
= общему числу молей газовой смеси
= общему давлению в газовой смеси
Мольная доля отдельного компонента в газовой смеси равна объёмной доле этого компонента в газовой смеси[5].
См. также[править | править код]
- Пар
- Газ, Идеальный газ и Уравнение состояния идеального газа
- Мольная доля и Моль
- Законы Дальтона
- Объёмный процент
- Закон Генри
Примечания[править | править код]
Источник
