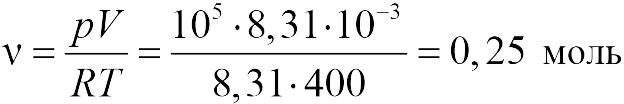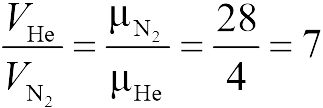Давление в сосуде от температуры

Добрый день наш уважаемый читатель. Получая часто вопросы от наших клиентов в 90% процентов из всех случаев, мы даем быстрые, четкие и грамотные ответы нашему собеседнику. Дело в том, что нашего богатого опыта работа отлично хватает чтобы закрыть потребности среднестатистического клиента или спикера.
Развернуто и не очень мы уже отвечали в нашем блоге людям на следующие вопросы:
Поставленная задача
Сейчас перед нами встала следующая задача вот такого содержания: есть сосуд с неизменяемым объемом жидкости внутри него. Предположим, что сосуд состоит из обыкновенного железа, например, возьмем простой накопительный бойлер (V = 50 литров). Начальное давление в системе 2 атмосферы, начальная температура воды Т1 = 17 градусов цельсия, конечная температура после нагрева Т2 = 57 градусов цельсия. Исходные параметры могут быть разные, но конечная задача, на которую нужно получить ответ будет следующая: какое давление будет в закрытом сосуде при нагреве воды до указанной температуры Т2, если учесть, что краны на сосуде (вход и выход) находятся в положении закрыто, и начальный объем не изменяется??? Давление можно снимать (измерять) при помощи встроенного или выносного трубного манометра. Расширительного бака нет. Все для эксперимента.
Остаемся на связи в любой момент! Компания Монтажник работает для Вас!
Закон и формула Шарля
Начав решать эту задачу, каждый может прибегнуть к такому ответу: «да ладно, это же задачка за 7 класс, тут нужно применять формулу известного физика Шарля, Вы что учебник физики не читали?». Далее следует решение:
Формула: (273+t2)/(273+t1)=коэффициент увеличения давления от исходного.
(273+57)/(273+17)=330/290=1.13.
1.13 умножаем на 2 получаем что давление будет равно 2.26 после нагрева жидкости с 17 до 57 на 40 единиц.
Ну дела, вот же решение, зачем страдать дальше? Но нет друзья, это решение конечно же хорошее – но применимо только для изохорных идеальных газов, но не в коем случае не для жидкости, представленной у нас на примере воды.
Едем дальше изучая попутно других известных святил физики, и воуля мы натыкаемся на еще одно решение.
Для расчетов берем исходные данные из чего изготовлен сосуд, у нас это железо. Коэффициент объёмного расширения железа стабильно одинаковый, берем за основу среднее значение 0,000036, а вот коэффициент объема воды изменяется в зависимости от ее нагрева. Примерно 0,00015 при 20 градусах цельсия и 0,00045 при 60 градусах цельсия. Среднее значение путем сложения из двух данных получаем 0,00030.
Чтобы посчитать объем во сколько увеличиться объем в сосуде воспользуемся формулой: 1 + коэффициент расширения железа * (t2-t1).
В цифрах будет выглядеть так: 1 + 0,000036 * (57 – 17) = 1.002;
В качестве информационной нагрузки узнаем еще на сколько бы увеличился V воды если бы она была вне сосуда: 1 + 0,0003 * (57 – 17) = 1,012. Далее все упирается на сколько же прочный Ваш сосуд и не раздует ли его при повышении давления.
Чтобы узнать процентное увеличение объема воды с воздействием на сосуд воспользуемся следующей формулой подставим все цифры: 1,012 / 1,002 * 100 – 100 = 1 %.
Обратившись к учебнику физики, мы узнаем, что при давлении каждой атмосферы объем воды уменьшается на 0,000006. Например, 50 литров, при одной атмосфере сожмется на 0,001 и будет 49.999. Зато по сравнению с газами сжимаемость жидкостей действительно ничтожна: в десятки тысяч раз меньше.
Если объём воды при 2 атм = 50 литров, то при 500 атм объём станет примерно на 1 литр меньше. (разница в двух числах 2%).
1%/2% * 500 = 250 атмосфер, то значение при котором по идее должно разорвать Ваш бак и то давление которое будет у вас при нагреве. Честно, считаем это какой-то бред и не он никак не сочетается с реальными жизненными показателями, полученными в ходе эксперимента.
Изучав дальше интернет и опираясь на наши знания всех из коллег нашего отдела было перепробовано масса различных вариантов и изучено мнений других людей, которые потом можно было бы использоваться для выявления формулы по нашей задаче:
Вода при нагревании увеличивается в объеме до 4%, т.е. 50 наших литров должны превратиться в 52 литра за счет ее расширения, но применить данную теорию в нашем вопросе нам пока не удалось. Мы даже изучили соотношение плотности льда к плотности воды и поняли объем в этом случае увеличивается на 11 процентов.
Есть мнение (алгоритм) с нашей стороны что ни одну из формул применить тут нельзя, так как в баке или бойлере представленным нами невозможно заполнить его на все 100% жидкостью, какую часть в одной жидкости все равно будет составлять воздух, который в этом случае будет работать как расширительный бак и возможно поэтому те 800 атмосфер которые получаются у разных людей нормализуются тем количеством воздуха который содержаться в сосуде.
Если Вы физик или технически подкованный человек, разбираетесь в данном вопросе и готовы разрешить наш спор и получить ответ на поставленную задачу – ждем Ваших решений под этой записью в комментариях.
Со своей стороны хотим так же сказать, что при проведении реального эксперимента и нагрева воды в бойлере с 18-20 градусов до 50, давление поднялось по манометру с 1.5 очков (бар, атмосфер) примерно и до 5 бар.
Спасибо за проявленный труд, терпение и прочтение данной статьи. Надеемся что этот вопрос решится в ближайшее время и мы найдем грамотный ответ.
Всего Вам доброго и приятного дня.
Другие полезные записи в блоге – только для Вас!
- Котел КСУВ наружного размещения. Почему он является лучшим из всех? Технические особенности, выбор большинства организаций. Котельная больше не нужна. Устанавливай прямо со зданием.
- История на “миллион”, как мы помогли ДОЛ “Лесное озеро”. Крупный DIY проект России, сделай сам!
- Тепловой пункт: какой промышленный котел выбрать?
- Наглядный ремонт КЧМ руками наших специалистов.
- ОАО “Кировский завод” банкрот. Какая судьба ожидает котлы КЧМ-5, КЧМ-5К, КЧМ-7 Гном?
- Почему в котлах КЧМ-5К не используются колосники? Техническая информация и не только.
- Все основные запасные части к котлу КЧМ, артикулы, описание и много полезной информации.
- Лемакс – лучшее соотношение цена/качество в бытовых котлах.
- 1000 колосников на складе компании МОНТАЖНИК – новый завоз.
- Что такое колосник? Расскажем все очень подробно.
- Почему котлы ИШМА покупают 90 из 100 клиентов. Лучшее соотношение цены-качества.
- Лучший конкурент котла Buderus, Valliant, Protherm – это Кентатсу (Kentatsu) – или как мы его называем один в поле ВОИН! А так же там мы ответили на вопрос, что лучше русский КЧМ или Турецкояпонский гигант?
- Полная подробная инструкция по монтажу промышленных котлов
- Посмотреть все статьи и новости
Наши отправки (отгрузки), услуги и выполненные работы:
Статьи посвященные нашим отгрузкам не только поднимают наш авторитет как считаем мы, но они направлены на увеличение доверия со стороны потенциальных клиентов. Нам нечего скрывать – мы делимся с Вами своими продажами и успехами. У нас нет скрытых продаж и ухода от налогов. Мы стараемся делать наше с Вами сотрудничество и работу максимально прозрачными. Мы хотим чтобы Вы доверяли нашей команде!
Если у Вас есть идеи о том, о том что Вы бы хотели увидеть на нашем канале. То присылайте их на нашу легкую почту: 426909@bk.ru. Если Вам понравилась статья оцените ее, поставьте палец вверх слева экрана (если Вы читаете ее с компьютера), а также подпишитесь на наш блог, Вас ждет много полезной и интересной информации.
С вами на связи была компания ООО “Монтажник” – официальный дистрибьютор нескольких заводов изготовителей по всей стране. По вопросам приобретения котлов, насосов и другого сопутствующего оборудования (запчасти, дымоходы, автоматика) можете обращаться по телефонам: 8(47354) 2-55-25; 2-69-09 или на электронную почту: 426909@bk.ru или montagnikvrn@yandex.ru.
Наш логотип
Отзывы о нашей компании:
15 лет на рынке – ни одного плохого отзыва за все время работы.
Посмотреть все отзывы.
СПАСИБО ЧТО ОСТАЕТЕСЬ С НАМИ! Рассказывайте друзьям, делитесь материалом со своими знакомыми. Нам важен каждый.
Компания которая относится к своему клиенту с ДУШОЙ!
Заказ через наш интернет магазин
Источник
Òåìïåðàòóðà êèïåíèÿ — ýòî òåìïåðàòóðà, ïðè êîòîðîé ïðîèñõîäèò êèïåíèå æèäêîñòè, êîòîðàÿ íàõîäèòñÿ ïîä ïîñòîÿííûì äàâëåíèåì. Ñîãëàñíî óðàâíåíèþ Êëàïåéðîíà — Êëàóçèóñà ñ ðîñòîì äàâëåíèÿ òåìïåðàòóðà êèïåíèÿ óâåëè÷èâàåòñÿ, à ñ óìåíüøåíèåì äàâëåíèÿ òåìïåðàòóðà êèïåíèÿ ñîîòâåòñòâåííî óìåíüøàåòñÿ. Óçíàòü êàê òåìïåðàòóðà êèïåíèÿ âîäû áóäåò çàâèñåòü îò äàâëåíèÿ âû ñìîæåòå èç òàáëèöû.
Çíà÷åíèÿ:
- tk,°C – òåìïåðàòóðà êèïåíèÿ âîäû (°C);
- P – îáùåå äàâëåíèå;
- êÏà – êèëîïàñêàëü;
- àòì. – àòìîñôåðà.
P | tk,°C | |
êÏà. | àòì. | |
0,981 | 0,01 | 6,698 |
1,961 | 0,02 | 17,20 |
3,923 | 0,05 | 28,64 |
9,807 | 0,1 | 45,45 |
19,61 | 0,2 | 59,67 |
29,42 | 0,3 | 68,68 |
39,23 | 0,4 | 75,42 |
49,03 | 0,5 | 80,86 |
58,84 | 0,6 | 85,45 |
68,65 | 0,7 | 89,45 |
78,45 | 0,8 | 92,99 |
88,26 | 0,9 | 96,18 |
98,07 | 1,0 | 99,09 |
101,3 | 1,033 | 100,00 |
147,1 | 1,5 | 110,79 |
196,1 | 2,0 | 119,62 |
245,2 | 2,5 | 126,79 |
294,2 | 3,0 | 132,88 |
392,3 | 4,0 | 142,92 |
490,3 | 5,0 | 151,11 |
588,4 | 6,0 | 158,08 |
686,5 | 7,0 | 164,17 |
784,5 | 8,0 | 169,61 |
882,6 | 9,0 | 174,53 |
980,7 | 10,0 | 179,04 |
1961 | 20,0 | 211,38 |
2452 | 25,0 | 222,90 |
4903 | 50,0 | 262,70 |
9807 | 100,0 | 309,53 |
Êàëüêóëÿòîðû ïî ôèçèêå | |
| Ðåøåíèå çàäà÷ ïî ôèçèêå, ïîäãîòîâêà ê ÝÃÅ è ÃÈÀ, ìåõàíèêà òåðìîäèíàìèêà è äð. | |
| Êàëüêóëÿòîðû ïî ôèçèêå | |
Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ôèçèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ôèçèêà 7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Источник
Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
| (13.1) |
где ![]() — давление газа,
— давление газа, ![]() — концентрация молекул газа (число молекул в единице объема),
— концентрация молекул газа (число молекул в единице объема), ![]() — постоянная Больцмана,
— постоянная Больцмана, ![]() — абсолютная (в шкале Кельвина) температура. Учитывая, что
— абсолютная (в шкале Кельвина) температура. Учитывая, что ![]() , где
, где ![]() — число молекул газа,
— число молекул газа, ![]() — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
— объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
| (13.2) |
Число молекул ![]() можно связать с количеством вещества газа
можно связать с количеством вещества газа ![]() :
: ![]() , где
, где ![]() — число Авогадро. Поэтому формулу (13.2) можно переписать в виде
— число Авогадро. Поэтому формулу (13.2) можно переписать в виде
| (13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как ![]() . Постоянная
. Постоянная ![]() = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу
= 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу ![]() и молярную массу этого газа
и молярную массу этого газа ![]()
| (13.3) |
С учетом (13.3) закон (13.2) можно переписать и в таком виде
| (13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
|
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
| (13.5) |
где ![]() — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
— постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
|
Второй график следует из соотношения
| (13.6) |
где ![]() — постоянная при постоянном объеме.
— постоянная при постоянном объеме.
Для изотермического процесса
|
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
| (13.7) |
где ![]() — постоянная. Отсюда следует, что графиком зависимости
— постоянная. Отсюда следует, что графиком зависимости ![]() от
от ![]() в изотермическом процессе является гипербола.
в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов ![]() определяется суммарным числом молекул всех компонент смеси:
определяется суммарным числом молекул всех компонент смеси:
| (13.8) |
где ![]() — число молекул первой, второй, третьей и т.д. компонент смеси,
— число молекул первой, второй, третьей и т.д. компонент смеси, ![]() — постоянная Больцмана,
— постоянная Больцмана, ![]() — абсолютная температура смеси,
— абсолютная температура смеси, ![]() — объем сосуда. Величины
— объем сосуда. Величины ![]() , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
, имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса ![]() :
:
|
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
|
где ![]() — искомый объем. Сравнивая первую и вторую формулы, заключаем, что
— искомый объем. Сравнивая первую и вторую формулы, заключаем, что ![]() (ответ 1).
(ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
|
где ![]() — неизвестная температура. Из сравнения этих формул получаем
— неизвестная температура. Из сравнения этих формул получаем ![]() , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
, т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
|
Отсюда ![]() , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
, т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. 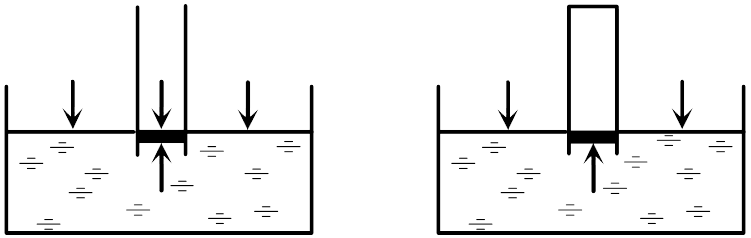 Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
 Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
 Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок)
В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
|
получим
|
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
|
(ответ 1).
Из уравнения состояния в форме ![]() (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода
(13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода ![]() и гелия
и гелия ![]() в задаче 13.2.1 равно 2 (ответ 2).
в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия | для азота |
где температуры ![]() и массы газов
и массы газов ![]() по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
|
(ответ 4).
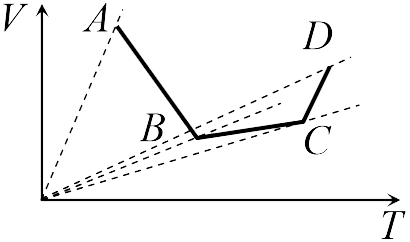
Если бы точки, отвечающие состояниям 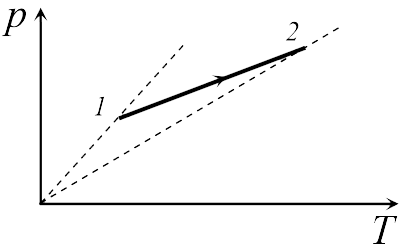 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед ![]() в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается
в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается ![]() (ответ 2).
(ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку ![]() (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
(поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
|
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном ![]() и начальном
и начальном ![]() состояниях получаем
состояниях получаем
|
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа ![]() и гелия
и гелия ![]() в сосуде в задаче 13.2.7 имеем
в сосуде в задаче 13.2.7 имеем ![]() (ответ 2).
(ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
|
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода ![]() (т.е. половина моля) и 3 • 1023 молекул гелия
(т.е. половина моля) и 3 • 1023 молекул гелия ![]() (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
(тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
|
(ответ 4). Здесь ![]() — масса газа,
— масса газа, ![]() — масса одной молекулы газа.
— масса одной молекулы газа.
Источник