Давление в сосуде с наклонными стенками

Эта статья описывает, как правильно строить эпюру гидростатического давления. Этот материал полезен в первую очередь студентам, изучающим курс механики жидкости и газа (гидравлики).

Эпюра давления — это графическое изображение распределения гидростатического давления по стенке или по длине какого-либо контура

Как правило, эпюру давления строят от избыточного гидростатического давления. О видах давления подробно можно прочитать в этойстатье сайта Проводу.рф.

Построение эпюры давления заключается в расчете давления в различных точках контура (стенки), на который давит жидкость, в и откладывании этой величины давления в виде отрезка перпендикулярно контуру в определенном масштабе.

Расчет давления выполняют по формуле (основное уравнение гидростатики):

Здесь Px — избыточное давление (превышение над атмосферным), Па; ρ — плотность жидкости, кг/м3 ; g — ускорение свободного падения, g = 9,81 м/с2 ; h — глубина (высота столба жидкости над точной), м.

Далее рассмотрим различные случаи, связанные с построением эпюры гидростатического давления — от самого простого к наиболее трудному.

1 Эпюра давления жидкости на вертикальную стенку

Когда мы имеем дело с вертикальной плоской стенкой, нам бессмысленно считать давление в каждой точке, достаточно всего в двух: сверху в месте, где находится свободная поверхность (уровень) жидкости — точка 1, и снизу на дне, точка 2.

В данном случае избыточное давление в точке 1: p1 = 0 Па,

Избыточное давление в точке 2: p2 = ρ g H.

2 Эпюра давления на наклонную стенку

Практически ничем не отличается случай, когда рассматривается давление на наклонную стенку. Значение давления, рассчитанное по основному уравнению гидростатики, откладывается перпендикулярно стенке. Опять же достаточно определить давление в двух точках — сверху и снизу. Сверху, если резервуар открытый, до давление будет равно 0 Па. Снизу на дне — ρ g h.

3 Эпюра давления на наклонную стенку + на поверхности жидкости есть избыточное давление

Если на поверхности жидкости есть избыточное давление p0, то его величина, согласно основному уравнению гидростатики, будет добавлена во всех точках наклонной стенки. Тогда к эпюре-треугольнику добавится еще прямоугольник, ширина которого равна p0 .

Итоговая эпюра будет иметь форму трапеции.

4 Эпюра давления на криволинейную поверхность

Построение эпюры давления на криволинейную поверхность требует вычисления давления во многих точках этой поверхности, а значения давления откладываются по нормали к соответствующим точкам. То есть нужно выбрать несколько точек ( сколько — зависит от масштаба схемы, но чтобы была возможность изобразить по этим точкам именно криволинейную, а не ломанную линию), и вычислить в них давление по основному уравнению гидростатики.

5 Эпюра двухстороннего давления, с двух сторон щита одинаковая жидкость

При наличии жидкости с двух сторон щита, необходимо строить отдельно две эпюры гидростатического давления (два треугольника — слева и справа). После этого эпюра справа вычитается из большой эпюры слева, и остается трапеция, которая учитывает давление и слева, и справа.

Т.е. наличие уровня жидкости справа частично компенсирует то давление, которое создает жидкость слева.

6 Эпюра двухстороннего давления, когда с двух сторон щита находятся жидкости с разными плотностями

Давление в сосуде с наклонными стенками

Здесь синим цветом показана эпюра для жидкости справа, которая «вырезается» из эпюры для жидкости слева. Т.е. во всех точках щита в той части, где вода находится с двух сторон, вычисляется разница давлений слева и справа. Эта разница и позволит построить результирующую эпюру давления (показана черным цветом).

7 Эпюра давления жидкости на стенку сложной формы, содержащую вогнутую область

Давление в сосуде с наклонными стенками

Принципиально данная задача ничем не отличается от предыдущих: в каждой точке контура мы вычисляем давление и в масштабе откладываем его значение по нормали к контуру.

С точки зрения графического построения, здесь возможно поступить следующим образом: сначала построить эпюру-треугольник. Он показывает, как увеличивается давление с глубиной. При этом он позволяет нам в виде отрезка получить давление в каждой точке. И дальше останется только перенести эти отрезки в соответствующие точки нашего контура. С верхней и нижней стенками при этом не должно возникнуть проблем. Эпюру для вогнутой области строим по принципу случая 4. Удобнее всего будет наметить несколько точек на этом вогнутом контуре, затем провести к ним касательные линии, и отложить значение давления, посчитанное заранее или взятое из треугольника в виде отрезка, перпендикулярно этим касательным. Эффект достигнут.

Источник

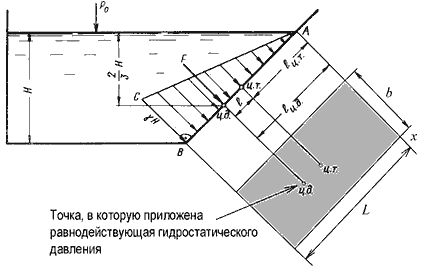
Пусть
мы имеем резервуар с наклонной правой
стенкой, заполненный жидкостью с удельным
весом γ. Ширина стенки в направлении,
перпендикулярном плоскости чертежа
(от читателя), равна b
Стенка условно показана развернутой
относительно оси АВ
и заштрихована на рисунке. Построим
график изменения избыточного
гидростатического давления на стенку
АВ.

Так
как избыточное гидростатическое давление
изменяется по линейному закон P=γgh, то
для построения графика, называемого
эпюрой давления, достаточно найти
давление в двух точках, например А
и B.

Давление в сосуде с наклонными стенками

Избыточное
гидростатическое давление в точке А
будет равно

PA
= γh
= γ·0 = 0

Соответственно
давление в точке В:

PB
= γh
= γH

где
H
– глубина жидкости в резервуаре.

Согласно
первому свойству гидростатического
давления, оно всегда направлено по
нормали к ограждающей поверхности.
Следовательно, гидростатическое давление
в точке В,
величина которого равна γH, надо направлять
перпендикулярно к стенке АВ.
Соединив точку А
с концом отрезка γH, получим треугольную
эпюру распределения давления АВС
с прямым углом в точке В.

Среднее
значение давления будет равно

Если
площадь наклонной стенки S=bL,
то равнодействующая гидростатического
давления равна

где
hc
= Н/2
– глубина погружения центра тяжести
плоской поверхности под уровень жидкости.

Однако
точка приложения равнодействующей
гидростатического давления ц.д. не
всегда будет совпадать с центром тяжести
плоской поверхности. Эта точка находится
на расстоянии l
от центра тяжести и равна отношению
момента инерции площадки относительно
центральной оси к статическому моменту
этой же площадки.

где
JАx
– момент инерции площади S
относительно центральной оси, параллельной
Аx.

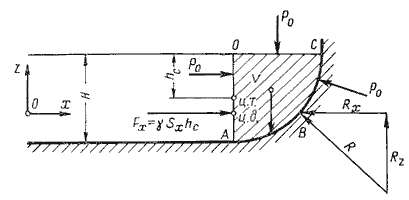
Определение
силы гидростатического давления на
произвольную криволинейную поверхность.

Пусть
жидкость заполняет резервуар, правая
стенка которого представляет собой
цилиндрическую криволинейную поверхность
АВС
(рис.2.2), простирающуюся в направлении
читателя на ширину b.
Восстановим из точки А перпендикуляр
АО
к свободной поверхности жидкости. Объем
жидкости в отсеке АОСВ
находится в равновесии. Это значит, что
силы, действующие на поверхности
выделенного объема V,
и силы веса взаимно уравновешиваются.

Давление в сосуде с наклонными стенками

Где
Рх
–
горизонтальная составляющая, которая
равна силе давления жидкости на плоскую
вертикальную проекцию криволинейной
поверхности.

Рх=
Рc*w=(Р0+γhc)*wz

Если
P0=Pатм.,
то Pх=
γhc*wz

Рc=
Р0+γhc–давление
в центре тяжести вертикальной проекции.

wz
–площадь
вертикальной проекции.(если криволинейная
поверхность цилиндрическая, то
вертикальная проекция прямоугольник;
если сферическая, то –круг или его
часть)

Рz–
вертикальная
составляющая, которая равна весу жидкости
в объеме тела давления.

Рz=γ*Wт.д.

Wт.д.
–
объем тела давления

Тело
давления
– фигура, ограничивающая криволинейной
поверхности вертикальную образующую,
проведенную из концов криволинейной
поверхности до уровня жидкости или его
продолжения и уровня жидкости.

Линия
действия силы Рz
всегда проходит через центр тяжести
тела давления, а вектор Рz
направлен вниз, если в теле давления
есть жидкость (т.е. «мокрое» +), Рz
направлено вверх, если в теле давления
жидкости нет (т.е. «сухое» -)

Линия
действия силы P
проходит под углом α=arttg

к горизонту через центр вращения круговой
поверхности.

Закон
Архимеда.

На
тело погруженное в жидкость действует
выталкивающая сила, направленная
вертикально вверх и равная весу жидкости,
в объеме погруженного в жидкость тела.

РА
=γ*W

Если
РА
>G,
то тело плавает на поверхности жидкости
Если
РА
=G,
то тело плавает, в полностью или частично
погруженном состоянии.
Если
РА
<G,
то тело тонет.

Способность
плавающего тела, выведенного из состояния
равновесия, вновь возвращаться в это
состояние называется устойчивостью.

Вес
жидкости, взятой в объеме погруженной
части судна называют водоизмещением,
а точку приложения равнодействующей
давления (т.е. центр давления) – центром
водоизмещения.
При нормальном положении судна центр
тяжести С
и центр водоизмещения d
лежат на одной вертикальной прямой
O’-O”,
представляющей ось симметрии судна и
называемой осью плавания .

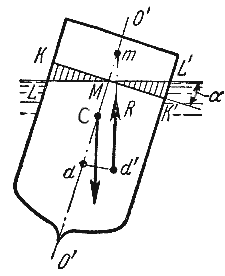
Пусть
под влиянием внешних сил судно наклонилось
на некоторый угол α, часть судна KLM
вышла из жидкости, а часть K’L’M’,
наоборот, погрузилось в нее. При этом
получили новое положении центра
водоизмещения d’.
Приложим к точке d’
подъемную силу R
и линию ее действия продолжим до
пересечения с осью симметрии O’-O”.
Полученная точка m
называется метацентром,
а отрезок mC
= h
называется метацентрической
высотой.
Будем считать h
положительным, если точка m
лежит выше точки C,
и отрицательным – в противном случае.

Давление в сосуде с наклонными стенками

Теперь
рассмотрим условия равновесия судна:

1)
если (С выше М) h
> 0, то судно возвращается в первоначальное
положение;
2) если (С совпадает с М) h
= 0, то это случай безразличного
равновесия;
3) если (С ниже М) h<0,
то это случай неостойчивого равновесия,
при котором продолжается дальнейшее
опрокидывание судна.

Следовательно,
чем ниже расположен центр тяжести и,
чем больше метацентрическая высота,
тем больше будет остойчивость судна.

Равновесие
жидкости в сообщающихся сосудах.

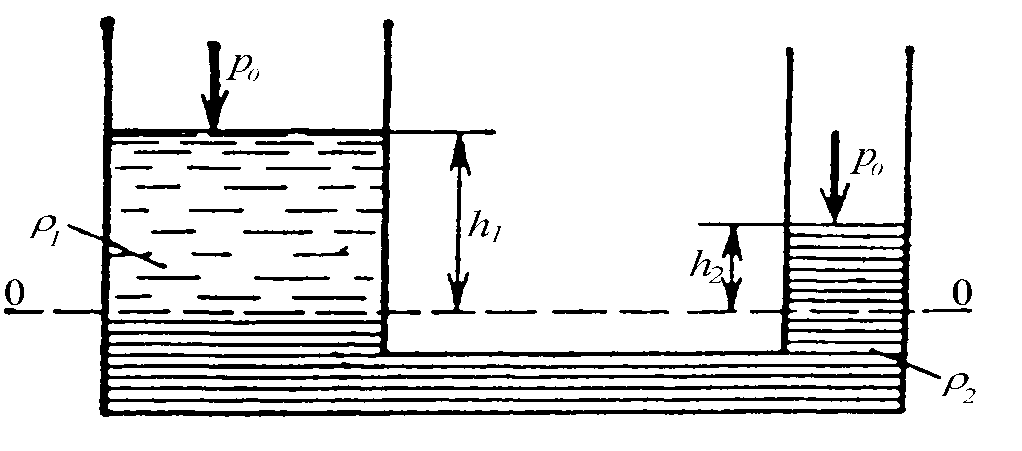
Рассмотрим
равновесие жидкости в сообщающихся
сосудах. Пусть на свободной поверхности
в обоих сосудах одинаковое внешнее
давление p. В общем
случае в сосудах разные жидкости с
плотностями р1и р2. Поверхность
раздела жидкости 0-0 является поверхностью
равного давления (z=const в однородной
жидкости). Уравнение равновесия
относительно горизонтальной плоскости
0-0 запишется в виде

Давление в сосуде с наклонными стенками

При
одинаковых давлениях на свободной
поверхности высоты двух разнородных
жидкостей над плоскостью раздела обратно
пропорциональны их плотностям.

Если
в сообщающихся сосудах жидкость
однородная, то свободная поверхность
в них устанавливается на одном уровне
(h1= h2).

Давление в сосуде с наклонными стенками

Объяснить
следующие понятия: установившиеся и
неустановившиеся движение; траектория
и линия тока; напорное и безнапорное
движение; равномерное движение.

Виды
движения:

Установившиеся

– такое движение, когда скорость и
давление жидкости в точках пространства,
заполненного жидкостью
Неустановившиеся.

U=f1(x,y,z,t)

P=1(x,y,z,t)

Траектория
–
путь отдельных частиц жидкости в
пространстве. Траектории могут
пересекаться, но только при неустановившемся
движении.

Линия
тока
– кривая в каждой точке, которой
направлена касательная, совпадает с
направлением вектора скорости частицы,
находящийся в данный момент времени в
этой точке. Линии тока никогда не
пересекаются!

Если
движение установившиеся, то траектория
и линии тока совпадают.

Если
сечение трубы полностью заполнено
жидкостью, то такое движение называется
напорным
движением.

Если
сечение трубы неполностью заполнено
жидкостью, т.е. есть свободная поверхность,
то такое движение называется безнапорным
движением.

Равномерное
движение —движение,
при котором тело за любые равные отрезки
времени проходит одинаковое расстояние.
Равномерное движение материальной
точки — это движение, при котором
скорость точки остаётся неизменной.

Вывести
уравнение неразрывности для струи.

Элементарная
струйка имеет ряд свойств:

Форма
элементарной струйки с течением времени
не меняется, т.к. не меняется положение
линии тока и ее образующая.
Жидкость
из элементарной струйки не попадает в
окружающей поток и из окружающего
потока в струйку.

При
установившимся движение элементарный
расход – величина постоянная для любого
сечения трубки.

dQ=const

Предположим:

dQ1>
dQ2
– неверно основании 2 свойства
dQ1<
dQ2
–
неверно на основании 2 свойства
dQ1=
dQ2
=>
=

u1dw1=u2dw2

Вывод
уравнения Бернулли для элементарной
струйки жидкости.

Теорема
механики об изменение кинетической
энергии:

∆Екин=∑А
∆Екин=Екин2-
Екин1

Екин1=dm*
;dm=ρ*dw=
*dw

Екин1=*dw
dw=Екин1=
*dw*

∆Екин=
γ*dw*(-)

Работа
сил тяжести, давления, трения.

Ав
=dG*(Z1-Z2)=
γ*dw*(Z1-Z2)
(сила
тяжести)

Ар=dP1*dl1
– dP2*dl2=P1dw*dl1-
P2dw*dl2
=dw*(P1-P2)
(сила
давления)

dw1*dl1=dW
= γ*dw*()

dw1*dl2=dW

В
итоге:

γ*dw*(-)=γ*dw*(Z1-Z2)
+ γ*dw*()

Z1++= Z2++

где:

Z1-удельная
потенциальная энергия положения
(геодезический напор)

–
удельная
потенциальная энергия давления
(пьезометрический напор)

Z1+=Hст–удельная
потенциальная энергия (гидростатический
напор)

удельная
кинетическая энергия (скоростной напор)

Z1++
– полная
удельная энергия (гидродинамический
напор)

Расход
и средняя скорость по сечению потока.
Вывод уравнения неразрывности для
потока. Дать понятие смоченного периметра
и гидравлического радиуса.

Расход
потока (Q)
– объем
жидкости, протекающий через живое
сечение в единицу времени.

Q=-расход
потока

Средняя
скорость(υ)–фиктивная
скорость, одинаковая для всех точек
живого сечения, при которой расход
остается тем же самым, что при истинных
скоростях.

Q=υ*w

υ==

υ=

Вывод
уравнения неразрывности для потока.

u1dw1=u2dw2

Q1=Q2=const

=u1*w1=u2*w2

Смоченный
периметр (χ)
– периметр потока, по которому происходит
трение жидкости о стенки трубы.

Гидравлический
радиус
– отношение площади живого сечения к
смоченному периметру.

Вывод
уравнения Бернулли для установившегося,
плавноизменяющегося потока жидкости.
Виды существующих потерь напора.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

При расчете резервуаров и различных емкостей для хранения жидкостей требуется знать полное давление жидкости на ограничивающие ее твердые стенки и точку приложения равнодействующей сил давления. Пусть задана плоская вертикальная стенка АВ (рис. 1.9).

Гидростатическое давление жидкости на всей площади поверхности стенки складывается из суммы гидростатических давлений во всех ее точках и называется суммарным давлением жидкости. Для определения этого давления необходимо установить, как оно распределяется по поверхности тела, на которое воздей-

Рис. 1.9. К определению силы гидростатического давления на плоскую поверхность:

а — эпюра гидростатического давления; б — положение центров тяжести и давления на плоской прямоугольной стенке

ствует жидкость. Графическое изображение распределения давления по высоте тела, например стенки, называется эпюрой гидростатического давления (см. рис. 1.9, а).

Гидростатическое давление в точке жидкости, расположенной на любой глубине от свободной поверхности, может быть определено по формуле (1.21)

Поверхностное давление в открытом сосуде, равное атмосферному давлению р0 = /?атм, передается в любую точку жидкости без изменения и является постоянным. Избыточное гидростатическое давление рgh пропорционально глубине погружения точки, т. е. изменение его значения по глубине подчинено линейному закону.

Атмосферное давление ратм, действующее на свободную поверхность жидкости и полностью передающееся в любую точку на стенке внутри жидкости, уравновешивается таким же атмосферным давлением, действующим снаружи на стенку сосуда. Поэтому при расчете стенок на прочность и устойчивость определяют и учитывают только избыточное давление р = рgh.

Эпюра избыточного гидростатического давления на вертикальную стенку сосуда приведена на рис. 1.9, а. Избыточное давление в точке А равно р = 0 (/? = 0), а в точке В — р = рgh.

В каждой точке жидкости давление нормально к поверхности стенки, поэтому на нормали к точке В откладываем в принятом масштабе отрезок BE, равный рgh, и соединяем прямой с точкой А. Треугольник АВЕ показывает распределение избыточного гидростатического давления по высоте стенки.

Каждая ордината этого треугольника представляет собой избыточное давление в соответствующей точке стенки, а площадь треугольника — силу суммарного избыточного давления жидкости на стенку в перпендикулярной ей плоскости. Если эту площадь умножить на ширину стенки Ь, то получим силу гидростатического давления, действующую на стенку сосуда:

Однако = hc, hb = F, следовательно

где F — площадь стенки, находящейся под поверхностью жидкости; hc — глубина погружения центра тяжести плоской поверхности (точка Сна рис. 1.9).

Сила избыточного давления, оказываемая на плоскую стенку, находящуюся под воздействием жидкости, равна произведению площади смоченной поверхности стенки на избыточное гидростатическое давление в ее центре тяжести. Это правило распространяется и на полное суммарное давление, и на любую плоскую фигуру, погруженную в жидкость. При учете поверхностного давления абсолютное суммарное давление, действующее на стенку, расчитывается по формуле:

Полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление рс в центре тяжести этой площади. Формула (1.28) справедлива и для любой наклонной плоскости с произвольными очертаниями.

Рис. 1.10. Гидростатический парадокс

Если стенка расположена горизонтально, т. е. является горизонтальным дном сосуда, то полная сила давления на дно Ран определяется по формулам

где h — высота столба жидкости над дном; F — площадь дна.

Сила давления на дно Рт зависит лишь от плотности жидкости, высоты столба жидкости и площади дна и не зависит от формы дна и объема сосуда, т. е. для сосудов разной формы давление на дно будет одинаковым, если они имеют одинаковую площадь дна и наполнены одинаковой жидкостью до одного и того же уровня. Это явление называется гидростатическим парадоксом, (рис. 1.10).

Точка приложения равнодействующей силы давления на стенку называется центром давления. Центр давления расположен ниже центра тяжести (точки С) (см. рис. 1.9). Только на горизонтальной стенке (дно сосуда) центр давления совпадает с центром тяжести. Положение центра давления легко определять графически. Равнодействующая сила давления проходит через центр тяжести эпюры. Проекция этого центра на плоскость стенки и есть центр давления. Для прямоугольной стенки равнодействующая силы гидростатического давления и центр давления находятся на расстоянии /?/3 от основания или 2/3/? от поверхности жидкости.

Координата центра давления yD, т. е. расстояние от свободной поверхности жидкости до центра давления, измеряемое вдоль стенки, может быть определена по формуле

где ус — расстояние от центра тяжести площади смоченной поверхности стенки до свободной поверхности жидкости, измеряемое вдоль стенки; /0 — момент инерции площади смоченной поверхности стенки относительно оси, проходящей через ее центр тяжести; F — площадь смоченной поверхности стенки.

Источник