Давление в сосуде с различными жидкостями

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июня 2020; проверки требуют 7 правок.

Гидростатическое давление – давление столба жидкости над условным уровнем.

Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине w этой поверхности, и направленной по нормали к ней. Отношение P/w, то есть давление р на поверхность, равную единице, называется гидростатическим давлением[1].

Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах[1].

Вычисление[править | править код]

В каждой жидкости существует давление, обусловленное её собственным весом ; так как , то ; учтём, что и получим формулу .

Плотность жидкости зависит от температуры. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением[2].

Для бытовых расчетов можно принять, что с ростом глубины на каждые 10 метров пресной воды, давление увеличивается на 0,1 МПа (1 атмосфера).

История открытия[править | править код]

Это основное свойство жидкостей было открыто и проверено на опыте Блезом Паскалем в 1653 г., хотя несколько ранее оно было уже известно Стевину[источник не указан 1297 дней].

Единица измерения[править | править код]

Единицей измерения давления в международной системе единиц является Паскаль. На практике гидростатическое давление часто измеряют в атмосферах, принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0 °C при нормальном ускорении свободного падения 9,80665 м/с².

На основании гидростатического парадокса можно гидростатическое давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности.

Свойства[править | править код]

Гидростатический парадокс[править | править код]

Гидростатическое давление на тело не зависит от направления.

Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние от каждой такой частицы до свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу гидростатического давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.

Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, гидростатическое давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.

Закон Паскаля[править | править код]

Чем глубже, тем выше давление. (левая часть графика)

Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести ( = несжимаемая жидкость) подчиняется закону Паскаля:

где:

– плотность [для пресной воды: ρ ≈ 1000 кг/м³] – ускорение свободного падения [для Европы: g ≈ 9,81 м/с²] – высота (здесь: жидкости) [м] – [Па]

⇒ = гидростатическое давление (p) зависит от высоты (h) жидкости.[4]

Примечания[править | править код]

Литература[править | править код]

В. В. Лермантов. Гидростатическое давление // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). – СПб., 1893. – Т. VIIIa. – С. 655-656.

Источник

Определение

Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.

Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.

Давление столба жидкости определяется формулой:

p = ρжgh

p – давление столба жидкости (Па), ρж- плотность жидкости (кг/м3), g – ускорение свободного падения (≈10 м/с2), h – высота столба жидкости, или ее глубина (м).

Важно! Высоту h нужно определять от поверхности жидкости.

Сила давления жидкости

Сила давления жидкости на дно сосуда – это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:

F = pS = ρжghab

Сила давления жидкости на боковую грань сосуда – это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:

F=ρжgh2hb

Подсказки к задачам:

Плотность пресной воды равна 1000 кг/м3.
Плотность соленой воды равна 1030 кг/м3.

Пример №1. Чему равно давление, созданное водой, на глубине 2 м?

Давление в жидкостях определяется формулой:

p = ρжgh.

Давление, созданное пресной водой, равно:

p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)

Давление, созданное соленой водой, равно:

p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)

Гидростатический парадокс

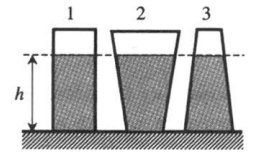
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.

p1 = p2 = p3

Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:

F1 < F2 < F3

Пример №2. На рисунке изображены три сосуда с разными жидкостями. Площади дна сосудов равны. В первом сосуде находится вода (ρ1 = 1 г/см3), во втором – керосин (ρ2 = 0,8 г/см3), в третьем – спирт (ρ3 = 0,8 г/см3). В каком сосуде оказывается максимальное давление на дно?

Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.

Задание EF18645

В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м2? Атмосферное давление не учитывать.

Алгоритм решения

Записать исходные данные и перевести единицы измерения величин в СИ.
Записать формулу для вычисления силы давления.
Выполнить решение задачи в общем виде.
Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

Высота сосуда H = 20 см.
Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
Площадь дна сосуда: S = 0,01 м2.

20 см = 0,2 м

2 см = 0,02 м

Сила давления равна произведению давления на площадь, на которую это давление оказывается:

F = pS

Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:

F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)

Ответ: 18

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF22709 Какова сила давления керосина, заполняющего цистерну, на заплату в её стене, находящуюся на глубине 2 м? Площадь заплаты 10 см2. Атмосферное давление не учитывать.

Алгоритм решения

Записать исходные данные и перевести единицы измерения величин в СИ.
Записать формулу для вычисления силы давления.
Выполнить решение задачи в общем виде.
Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

Глубина заплаты в цистерне h = 2 м.
Площадь заплаты: S = 10 см2.

10 см2 = 0,001 м2

Сила давления равна произведению давления на площадь, на которую это давление оказывается:

F = pS

Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:

F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)

Ответ: 16

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18804

На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.

Выберите два верных утверждения, согласующихся с приведёнными графиками.

Ответ:

а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.

б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.

в) Плотность керосина 0,82 г/см3, аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.

г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.

д) Плотность оливкового масла 0,92 г/см3, аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).

Алгоритм решения

1.Проверить все утверждения на истинность.

2.Записать буквы, соответствующие верным утверждениям, последовательно без пробелов.

Решение

Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.

Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.

Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.

Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.

Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.

Верный ответ: бд.

Ответ: бд

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | ???? Скачать PDF | Просмотров: 1.8k | Оценить:

Источник

II. Молекулярная физика

Тестирование онлайн

Давление

Это физическая скалярная величина, которая определяется по формуле

Атмосферное давление

Атмосфера – это воздушная оболочка Земли, которая удерживается гравитационными силами. Атмосфера имеет вес и давит на все тела на Земле. Давление атмосферы составляет около 760 мм.рт.ст. или 1 атм., или 101325Па. Миллиметр ртутного столба, атмосфера – это различные внесистемные единицы измерения давления. Атмосферное давление уменьшается на 1 мм.рт.ст. при поднятии над Землей на каждые 11м.

Что такое давление в 1 атм? Рукопожатие крепкого мужчины составляет 0,1 атм, удар боксера составляет несколько атмосферных единиц. Давление каблука-шпильки составляет 100 атмосфер. Если на ладонь положить гирю в 100 кг, то получим неравномерное давление в одну атмосферу, при погружении на 10 м под воду получим равномерное давление в 1 атмосферу. Равномерное давление легко переносится человеческим организмом. Нормальное атмосферное давление, которое действует на каждого человека, компенсируется внутренним давлением, поэтому его мы совершенно не замечаем, несмотря на то, что оно является достаточно существенным.

Закон Паскаля

Давление на жидкость или газ передается во всех направлениях одинаково.

Давление внутри жидкости (газа) на одной и той же глубине одинаково во всех направлениях (влево вправо, вниз и вверх!)

Гидростатическое давление

Это давления столбика жидкости на дно сосуда. Какая сила создает давление? Жидкость обладает весом, который давит на дно.

Давление жидкости на дно

Давление на дно сосуда не зависит от формы сосуда, но зависит от площади его дна. При этом сила давления на дно может быть и больше и меньше силы тяжести жидкости в сосуде. В этом заключается «гидростатический парадокс».

На стенку сосуда гидростатическое давление распределено неравномерно: у поверхности жидкости оно равно нулю (без учета атмосферного давления), внутри жидкости изменяется прямо пропорционально глубине и на уровне дна достигает значения

. Это переменное давление можно заменить средним давлением

Сообщающиеся сосуды

Это сосуды, которые имеют общий канал внизу.

Однородная жидкость устанавливается в сообщающихся сосудах на одном уровне независимо от формы сосудов, как видно на фотографии.

Разнородные жидкости устанавливаются в сообщающихся сосудах согласно формуле

Гидравлический пресс

Гидравлический пресс состоит из двух сообщающихся сосудов цилиндрической формы. В сосудах двигаются поршни с площадями S1 и S2. Цилиндры заполнены техническим маслом.

Объем жидкости, вытесненный малым поршнем поступает в большой цилиндр.

Гидравлический пресс дает выигрыш в силе во столько раз, во сколько площадь большего поршня больше площади меньшего. Выигрыша в работе гидравлический пресс не дает.

На практике вследствие наличия трения:

Давление не перпендикулярной к поверхности силы

Если сила направлена под углом к нормали (перпендикуляру), то давление определяется по формуле

Практическое применение

Газы и жидкости, находящиеся под давлением, нашли широкое применение в промышленной технике. Например, пневматический отбойный молоток. При помощи сжатого воздуха работают также двери в автобусах и метро, тормоза поездов и грузовых автомобилей.

Встречаются также механизмы, работающие при помощи сжатой жидкости. Они называются гидравлическими. Например, устройство гидравлического пресса.

Атмосферное давление открытие и измерение

Численное значение атмосферного давления было определено опытным путем в 1643 году итальянским ученым Э.Торричелли.

Стеклянную трубку длиной около метра, запаянную с одного конца, наполняют доверху ртутью. Затем, плотно закрыв отверстие пальцем, трубку переворачивают и опускают в чашу со ртутью, после чего палец убирают. Ртуть из трубки начинает выливаться, но не вся: остаётся «столб» » 76 см высотой, считая от уровня в чаше. Примечательно, что эта высота не зависит ни от длины трубки, ни от глубины её погружения.

Атмосферное давление уравновешивает гидростатическое давление столбика ртути. Согласно закону Паскаля давление атмосферы давит вверх на столбик ртути. А столбик ртути давит вниз своим весом. Ртуть перестает опускаться, когда эти давления одинаковые. Вычислив гидростатическое давление ртути известной высоты, определили давление атмосферы.

Трубка Торричелли с линейкой является простейшим барометром – прибором для измерения атмосферного давления

Для измерения атмосферного давления используют также барометр-анероид.

Поскольку атмосферное давление уменьшается по мере удаления от поверхности Земли, то шкалу анероида можно проградуировать в метрах. В этом случае он называется альтиметром.

Возникновение силы Архимеда

Пусть прямоугольный металлический брусок площадью основания S и высотой h лежит на дне сосуда, в который налита вода до высоты H, H>h. Как определить силу давления бруска на дно сосуда?

Возможны два случая! Пусть брусок неплотно прилегает ко дну сосуда, тогда снизу на брусок действует сила давления жидкости. Эта сила больше силы давления жидкости сверху, поэтому возникает сила Архимеда. Сила Архимеда – результат разницы силы гидростатического давления на нижнюю грань бруска и верхнюю грань, зависит от высоты бруска и площади основания.

Используем 2 закон Ньютона:

Рассмотрим второй возможный случай. Пусть брусок прилегает ко дну так плотно, что жидкость под него не подтекает. Снизу отсутствует давление жидкости, следовательно сила Архимеда равна нулю. Сверху же на брусок действует сила давления жидкости и атмосферы.

Используем 2 закон Ньютона для этого случая:

p – атмосферное давление,

p – гидростатическое давление столба жидкости высотой H-h.

Источник

Гидростатический парадокс или парадокс Паскаля

Гидростатический парадокс или парадокс Паскаля – явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равна весу жидкости лишь для сосуда цилиндрической формы. Математическое объяснение парадоксу было дано Симоном Стевином в 1612 году.

Причины

Причина гидростатического парадокса состоит в том, что по закону Паскаля жидкость давит не только на дно, но и на стенки сосуда.

Если стенки сосуда вертикальные, то силы давления жидкости на его стенки направлены горизонтально и не имеют вертикальной составляющей. Сила давления жидкости на дно сосуда в этом случае равна весу жидкости в сосуде. Если же сосуд имеет наклонные стенки, давление жидкости на них имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда, поэтому он и отличается от давления на дно.

Опыт Паскаля

В 1648 году парадокс продемонстрировал Блез Паскаль . Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Гидростатический парадокс и закон Архимеда

Похожий кажущийся парадокс возникает при рассмотрении закона Архимеда . Согласно распространённой формулировке закона Архимеда , на погружённое в воду тело действует выталкивающая сила, равная весу воды, вытесненной этим телом. Из такой формулировки можно сделать неверное умозаключение, что тело не сможет плавать в сосуде, не содержащем достаточное количество воды для вытеснения.

Однако на практике тело может плавать в резервуаре с таким количеством воды, масса которой меньше массы плавающего тела. Это возможно в ситуации, когда резервуар лишь ненамного превышает размеры тела. Например, когда корабль стоит в тесном доке, он остаётся на плаву точно так же, как в открытом океане, хотя масса воды между кораблём и стенками дока может быть меньше, чем масса корабля.

Объяснение парадокса заключается в том, что архимедова сила создаётся гидростатическим давлением, которое зависит не от веса воды, а только от высоты её столба. Как в гидростатическом парадоксе на дно сосуда действует сила весового давления воды, которая может быть больше веса самой воды в сосуде, так и в вышеописанной ситуации давление воды на днище корабля может создавать выталкивающую силу, превышающую вес этой воды.

Более корректной формулировкой закона Архимеда является следующая: на погружённое в воду тело действует выталкивающая сила, эквивалентная весу воды в погружённом объёме тела.

Источник