Давление жидкостей и газов на стенки и дно сосуда
Закон Паскаля: давление, производимое на жидкость или газ, передается жидкостью или газом во все стороны одинаково.
Такая особенность передача давления жидкостями и газами связана с подвижностью молекул в жидком и газообразном состояниях.
Давление столба жидкости определяется формулой:
p = ρжgh
p — давление столба жидкости (Па), ρж— плотность жидкости (кг/м3), g — ускорение свободного падения (≈10 м/с2), h — высота столба жидкости, или ее глубина (м).
Важно! Высоту h нужно определять от поверхности жидкости.
Сила давления жидкости
Сила давления жидкости на дно сосуда — это произведение давления, оказываемого жидкостью на дно сосуда, на площадь этого дна:
F = pS = ρжghab
Сила давления жидкости на боковую грань сосуда — это произведение половины давления, оказываемого жидкостью на дно сосуда, на площадь грани:
F=ρжgh2hb
Подсказки к задачам:
- Плотность пресной воды равна 1000 кг/м3.
- Плотность соленой воды равна 1030 кг/м3.
Пример №1. Чему равно давление, созданное водой, на глубине 2 м?
Давление в жидкостях определяется формулой:
p = ρжgh.
Давление, созданное пресной водой, равно:
p = 1000∙10∙2 = 20000 (Па) = 20 (кПа)
Давление, созданное соленой водой, равно:
p = 1030∙10∙2 = 20600 (Па) = 20,6 (кПа)
Гидростатический парадокс
Из закона Паскаля следует, что давление на дно сосуда определяется только плотностью жидкости и высотой ее столба. Поэтому, если в разные сосуды налить одинаковую жидкость одинаковой высоты, давление, оказываемое ею на дно каждого из сосудов, будет одинаковым.
p1 = p2 = p3
Сила давления при этом будет разная, так как она прямо пропорционально зависит от площади дна. Так как площадь дна первого сосуда минимальна, а третьего максимальна, силы давления, оказываемые жидкостью на дно сосудов, будут такими:
F1 < F2 < F3
Пример №2. На рисунке изображены три сосуда с разными жидкостями. Площади дна сосудов равны. В первом сосуде находится вода (ρ1 = 1 г/см3), во втором — керосин (ρ2 = 0,8 г/см3), в третьем — спирт (ρ3 = 0,8 г/см3). В каком сосуде оказывается максимальное давление на дно?
Давление зависит только от плотности жидкости и от ее столба: площадь сосудов никакой роли не играет. Так как столбы жидкостей во всех сосудах одинаково, остается сравнивать плотности. Плотность воды больше плотности керосина и плотности спирта. Поэтому в сосуде 1 давление на дно сосуда будет максимальным.
В сосуд высотой 20 см налита вода, уровень которой ниже края сосуда на 2 см. Чему равна сила давления воды на дно сосуда, если площадь дна 0,01м2? Атмосферное давление не учитывать.
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Высота сосуда H = 20 см.
- Разница между высотой сосуда и уровнем налитой в него воды: b = 2 см.
- Площадь дна сосуда: S = 0,01 м2.
20 см = 0,2 м
2 см = 0,02 м
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. А высота столба воды в данном случае равна разности высоту стакана и разнице между высотой сосуда и уровнем воды. Поэтому:
F = pS = ρжghS = ρжg(H – b)S = 1000∙10∙(0,2 – 0,02)∙0,01 = 18 (Н)
Ответ: 18
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Записать формулу для вычисления силы давления.
- Выполнить решение задачи в общем виде.
- Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
- Глубина заплаты в цистерне h = 2 м.
- Площадь заплаты: S = 10 см2.
10 см2 = 0,001 м2
Сила давления равна произведению давления на площадь, на которую это давление оказывается:
F = pS
Давление равно произведению высоты столба жидкости на ускорение свободного падения и на плотность самой жидкости. Поэтому:
F = pS = ρкghS = 800∙10∙2∙0,001 = 16 (Н)
Ответ: 16
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке представлены графики зависимости давления p от глубины погружения h для двух покоящихся жидкостей: воды и тяжёлой жидкости дийодметана, при постоянной температуре.
Выберите два верных утверждения, согласующихся с приведёнными графиками.
Ответ:
а) В воде на глубине 25 м давление p в 2,5 раза больше атмосферного.
б) С ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде.
в) Плотность керосина 0,82 г/см3, аналогичный график зависимости давления от глубины для керосина окажется между графиками для воды и дийодметана.
г) Если внутри пустотелого шарика давление равно атмосферному, то в воде на глубине 10 м давления на его поверхность извне и изнутри будут равны друг другу.
д) Плотность оливкового масла 0,92 г/см3, аналогичный график зависимости давления от глубины для масла окажется между графиком для воды и осью абсцисс (горизонтальной осью).
Алгоритм решения
1.Проверить все утверждения на истинность.
2.Записать буквы, соответствующие верным утверждениям, последовательно без пробелов.
Решение
Проверим истинность первого утверждения (а). Для этого определим по графику давление воды на глубине 25 м. Если пустить перпендикуляр к графику зависимости давления воды от глубины погружения через h = 25 м, то он пересечет график в точке, которой соответствует давление p = 350 кН. Атмосферное давление равно 100 кН. Следовательно, давление воды на этой глубине в 3,5 раза превышает атмосферное давление. Утверждение неверно.
Проверим второе утверждение (б). Согласно ему, с ростом глубины погружения давление в дийодметане возрастает быстрее, чем в воде. Это действительно так, потому что угол наклона графика зависимости давления дийодметана от глубины погружения к оси абсцисс больше того же графика для воды. Это можно подтвердить и математически: давление в более плотной жидкости с глубиной растет быстрее, так как давление имеет прямо пропорциональную зависимость с глубиной. Утверждение верно.
Проверим третье утверждение (в). Согласно ему, если на этом же рисунке построить график зависимости давления керосина от глубины погружения, то он окажется между двумя уже существующими графиками. Но этого не может быть, потому что давление в воде растет медленнее, чем давление в дийодметане, так как вода менее плотная. По этой же причине давление в керосине будет расти медленнее, чем в воде, так как керосин менее плотный по сравнению с водой. Третий график в этом случае займет положение между графиком зависимости давления воды от глубины погружения и осью абсцисс. Утверждение неверно.
Проверим четвертое утверждение (г). Согласно графику, давление воды на глубине 10 м равно 200 кПа. Поэтому давление на поверхность шарика снаружи, погруженного на такую глубину, будет вдвое больше, чем давление, оказываемое на его стенки изнутри (при условии, что давление внутри равно 1 атм.). Утверждение неверно.
Проверим последнее утверждение (д). Согласно ему, если на этом же рисунке построить график зависимости давления оливкового масла от глубины погружения, то он окажется между графиком для воды и осью абсцисс. Это действительно так, потому что плотность оливкового масла меньше плотности воды. Утверждение верно.
Верный ответ: бд.
Ответ: бд
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | ???? Скачать PDF | Просмотров: 1k | Оценить:
Источник
Содержание:
- § 1 Особенности давления в жидкости и газе
- § 2 Формула для вычисления давления в жидкостях и газах
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги по теме урока
§ 1 Особенности давления в жидкости и газе
Известно, что давление, производимое на жидкости и газы, передается в каждую точку без изменения по всем направлениям. Это утверждение называется законом Паскаля.
На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому верхние слои жидкости давят на нижележащие слои, это давление по закону Паскаля передается по всем направлениям. Значит, внутри жидкости существует давление. Чтобы убедиться в этом, поставим опыт.
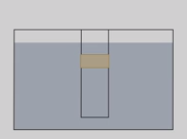
Возьмем стеклянную трубочку, затянутую снизу резиновой пленкой. Если в трубочку нальем воду, то увидим, что резиновая пленка прогибается. На резиновую пленку действуют две силы: вес воды, направленный вниз, из-за чего пленка изменяет свою форму, и возникающая при деформации сила упругости, которая стремится восстановить первоначальную форму и направленная вверх. Если две эти силы равны, то пленка будет находиться в покое.
Опустим трубку с водой в другой, более широкий, сосуд с водой. Возникает третья сила, действующая на резиновую пленку, – сила давления воды снизу, она направлена вверх и заставляет пленку выпрямляться. Если уровни воды в трубке и в сосуде совпадут, то силы давления, действующие сверху и снизу на пленку, окажутся равными.

Такой же опыт проведем с трубкой, в которой есть боковое отверстие, затянутое резиновой пленкой. Если в трубку налить воду, то пленка выгибается наружу, так как вода давит не только на дно трубки, но и на стенки. Опустим трубку в воду и заметим, что пленка выпрямляется, то есть силы, действующие на пленку изнутри и снаружи, оказались равными.
Итак, опыты показывают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям.
Такое же утверждение справедливо и для газов.
§ 2 Формула для вычисления давления в жидкостях и газах
От чего зависит давление в жидкостях и газах?
Вспомним определение давления.
Давление – скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: p = F/S.
Сила давления Fравна весу P: P = mg.
Мы знаем, что массу тела можно найти по плотности вещества: m = ρV, где ρ – плотность, V – объем.
Объем жидкости, находящейся в сосуде в форме прямоугольного параллелепипеда или в форме цилиндра, можно найти, умножив площадь дна на высоту сосуда: V = Sh. Подставим формулы веса, массы, объема в формулу давления и, сократив площадь, получим:
Мы вывели формулу для вычисления давления в жидкостях и газах:
p = gρh.
Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
По формуле p = gρhможно рассчитывать:
1)давление жидкости на дно в сосуде любой формы, то есть давление жидкости не зависит от формы сосуда;
2)давление жидкости на стенки сосуда, так как давление на одной и той же глубине одинаково по всем направлениям: вверх, вниз, вправо, влево, вперед, назад;
3)давление в газах.
Проверим единицу измерения давления по формуле p = gρh.
g – коэффициент тяжести, измеряется в Н/кг,
ρ – плотность, в международной системе единиц измеряется в кг/м3,
h – высота столба жидкости (глубина) – в м.
§ 3 Решение задачи по теме урока
Рассмотрим решение задачи:
Задача:Определить давление воды на дно морской впадины, глубина которой 10900 м. Плотность морской воды – 1030 кг/м3.
Решение: Запишем условие задачи: нам известны глубина h = 10900 м, плотность ρ = 1030 кг/м3. Необходимо найти: давление p. Для решения: запишем формулу расчета давления в жидкостях и газах p = gρh и подставим числовые значения:
p = 10 Н/кг · 1030 кг/м3· 10 900 м = 112 270 000 Па = 112, 27 МПа.

Ответ: 112, 27 МПа
§ 4 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
На жидкости и газы действует сила тяжести, поэтому они обладают весом. Вышележащие слои жидкости и газа своим весом давят на нижележащие слои, то есть оказывают давление. Давление внутри жидкости и газа на одном и том же уровнеодинаково по всем направлениям.
Давление в жидкостях и газах рассчитывается по формуле p = gρh, где g – коэффициент тяжести, ρ – плотность, h – высота столба жидкости или газа.
Давление в жидкостях и газах зависит только от плотности и высоты столба жидкости или газа и не зависит от формы и площади поперечного сечения сосуда, в котором находится жидкость или газ.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября”, 2002. – 272 с.
Источник
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа с. Селихово
Конаковского района Тверской области
Конспект урока
«Давление в жидкости и газе. Расчёт давления жидкости на дно и стенки сосуда»,
Физика 7 класс.
Автор: Кейля Олеся Сергеевна.
учитель физики
2018 г
Конспект урока «Давление в жидкости и газе. Расчёт давления жидкости на дно и стенки сосуда», Физика 7 класс.
Тема урока: Давление в жидкости и газе. Расчёт давления жидкости на дно и стенки сосуда.
Тип урока: урок изучения нового материала
Оборудование: компьютер, набор демонстрационного оборудования «Давление в жидкости», видеоролики и презентации.
Учащиеся владеют:
регулятивными УУД:
– формулировать вопросы по теме на основе опорных слов;
познавательными УУД;
– выделять и структурировать информацию, существенную для решения проблемы, под руководством учителя;
личностные УУД:
– осуществляют рефлексию своего отношения к содержанию темы по заданному алгоритму.
У учащиеся недостаточно сформированы:
коммуникативные УУД:
– эффективно сотрудничать, осуществляя взаимопомощь и взаимоконтроль.
Цели урока: познакомить учащихся с понятием давления в жидкости и газе, выяснить от чего оно зависит и как его можно рассчитать.
Задачи:
образовательные: расширить представление о давлении в жидкости газе;
развивающие: формирование УУД у учащихся при решении задач;
воспитательные: политехническое воспитание через изучение способов измерения давления, уважение труда и точки зрения одноклассников.
План урока:
Мотивационно-целевой этап
Ориентировочный этап
Поисково-исследовательский этап
Практический этап
Рефлексивно-оценочный этап
Мотивационно-целевой этап
Учитель. Здравствуйте ребята! Сегодня мы свами продолжим знакомиться с понятием ДАВЛЕНИЕ. Давайте для начала вспомним то что мы уже знаем о давлении.
Проводится фронтальный опрос.
От чего зависит давление тела на поверхность? (F, S)
Назовите формулу для расчета давления тела на поверхность. (p=F/S)
Чем создается давление газа в сосуде? (ударами молекул о стенки сосуда)
Как можно изменить давление газа в сосуде? (изменить: объем сосуда, температуру газа, количество молекул в сосуде)
Как передается давление в жидкостях и газах? (без изменений во всех направлениях, закон Паскаля)
Как передается давление в твердых телах? (в направлении действия силы)
Учащиеся заполняют таблицу «Знаю. Хочу знать. Узнал», графу «Знаю».
Учитель. А теперь давайте перейдем к новой теме. Для этого проведём небольшой опыт.
Демонстрирует опыт: Сосуд, заполненный водой, имеет три отверстия, на разных уровнях. Отверстия закрыты пробками. Если убрать пробки, то образуется три струи с разным напором воды.
Учитель.Сформулируйте вопросы, которые у вас возникают в результате наблюдения и запишите их в таблицу в графе «Хочу знать».
Ученики записывают вопросы: Почему струи воды на разных уровнях имеют разный напор? От чего зависит давление в жидкости на разных уровнях? Как рассчитать давление в жидкости?
Учитель.Исходя из ваших вопросов, сформулируем тему нашего урока.
Ученики совместно с учителем формулируют тему урока.
Ориентировочный этап
Учитель. Давайте подумаем, где мы можем найти информацию для ответа на те вопросы, которые вы записали.
Ученики отвечают, что информацию можно найти в учебнике, в энциклопедии, интернете, спросить у учителя, провести эксперимент.
Учитель. Хорошо. Предлагаю вам следующий порядок работы: каждый из вас получит задание – провести эксперимент и объяснить его.
Ученики соглашаются с предложенным порядком работы.
Поисково-исследовательский этап
Учитель выдает каждому задание с описанием опыта. Инструктирует по ходу работы.
Ученики знакомятся с опытом, проводят его, демонстрируют и объясняют результаты одноклассникам.
Опыт 1. Наливаем воду в стеклянную трубку, дно которой закрыто резиновой плёнкой. Под действием веса жидкости дно трубки прогнётся. При этом, чем выше столб жидкости, тем больше деформация резиновой плёнки. Вода в трубке находится в равновесии, значит, сила тяжести, и сила упругости уравновешивают друг друга.
Опыт 2. Трубку с водой опускаем в сосуд, наполненный водой. Замечаем, по мере погружения трубки резиновая плёнка постепенно выпрямляется. Как только уровни воды в трубке и сосуде совпадут, плёнка будет полностью выпрямлена.
Как можно объяснить, что теперь нет деформации резиновой плёнки? (Это означает, что силы, действующие на плёнку, одинаковы с двух сторон)
Опыт 3. Такая же труба, только с боковым отверстием, которое закрыто резиновой плёнкой. Результат погружения: плёнка выпрямляется, как только уровни воды в сосуде и трубке будут одинаковыми. (Это означает, что силы, действующие на плёнку, одинаковы с двух сторон)
Опыт 4. Трубка с водой, дно может отпадать. При погружении в воду, как только уровни воды в трубке и сосуде совпадают, дно отпадает под действием силы тяжести.
Вывод: внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям; с глубиной давление увеличивается.
Учитель просит зафиксировать результаты опытов, которые являются ответами на поставленные вопросы, задавать вопросы если, что то, не ясно.
Ученики записывают в полученную информацию в тетрадь, задают при необходимости вопросы.
Учитель.Мы узнали, что давление зависит от плотности жидкости и от глубины погружения или от высоты столба жидкости. Теперь рассмотрим, как можно рассчитать давление жидкости на дно и стенки сосуда. Решим задачу для сосуда, который имеет форму параллелепипеда, например аквариум или бассейн.
Ученики совместно с учителем выводят формулу для расчёта давления на дно и стенки сосуда.
Задача 1. Рассчитайте давление, которое производит вода высотой 50см на дно аквариума.
СИ
Решение:
h = 50см
ρ = 1
g = 9,8
0,5м
1000
1. p = , где F=P
2. P = g •m, где m=ρ•V, V=S•h; P = g • ρ•V
3. p = = =g •ρ•h
4.[p]= []= []=[Па]
5.p =9,8•1000•0,5=4900(Па) ≈ 5000(Па)
p –?
Из формулы давления жидкости на дно и стенки сосуда следует, что это давление зависит от таких физических величин как плотность вещества и высота столба жидкости (глубина): чем больше плотность и высота столба жидкости, тем больше давление.
Практический этап
Учитель. Ребята, давайте обобщим полученные знания. Для этого ответим на несколько вопросов.
Как меняется давление в жидкости с глубиной погружения? (с увеличением глубины давление в жидкости возрастает)
Одинаковое ли давление действует в разных направлениях в жидкости на одном и том же уровне? (да)
Зависит ли давление жидкости на дно сосуда от площади дна? (нет)
От чего зависит давление жидкости на дно и стенки сосуда? (от плотности жидкости и высоты столба жидкости)
Ученики отвечают на вопросы.
Учитель дает ученикам решить задачу на применение формулы для расчета давления жидкости на дно и стенки сосуда, показывает алгоритм решения.
Задача 2. Рассчитайте давление, которое производит нефть высотой 150см на дно бака.
СИ
Решение:
h = 150см
ρ = 0,8
g = 9,8
1,5м
800
1. p=g •ρ•h
2. [p]= []= []=[Па]
3.p =9,8•800•1,5=11760(Па) ≈ 12000(Па)
p –?
Ученики решают задачу по алгоритму.
Рефлексивно-оценочный этап
Учитель. А теперь давайте подведем итоги. Заполните в вашей таблице графу «Узнал» и определите получили ли вы ответы на все поставленные вопросы.
Ученики заполнят таблицу и оценивают степень достижения цели урока.
Учитель задает домашнее задание (§39, §40, упр. 17) и дает инструкции по его выполнению. Ученики записывают домашнее задание и слушают инструкции учителя.
Источник
