Давление жидкости на дно цилиндрического сосуда зависит
Главная Онлайн учебники База репетиторов России Тренажеры по физике Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Элементы статики
1.15. Элементы гидростатики
Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, скользя друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы.
На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил вводится новая физическая величина – давление.
Давление определяется как отношение модуля силы действующей перпендикулярно поверхности, к площади S этой поверхности:
В системе СИ давление измеряется в паскалях (Па):
Часто используются внесистемные единицы: нормальная атмосфера (атм) и миллиметр ртутного столба (мм Hg):
1 атм = 101325 Па = 760 мм Hg.
Французский ученый Б. Паскаль в середине XVII века эмпирически установил закон, названный законом Паскаля:
Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.
Для иллюстрации закона Паскаля на рис. 1.15.1 изображена небольшая прямоугольная призма, погруженная в жидкость. Если предположить, что плотность материала призмы равна плотности жидкости, то призма должна находиться в жидкости в состоянии безразличного равновесия. Это означает, что силы давления, действующие на грани призмы, должны быть уравновешены. Это произойдет только в том случае, если давления, т. е. силы, действующие на единицу площади поверхности каждой грани, одинаковы: p1 = p2 = p3 = p.
| Рисунок 1.15.1. Закон Паскаля: p1 = p2 = p3 = p |
Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости. Сила давления на дно цилиндрического сосуда высоты h и площади основания S равна весу столба жидкости mg, где m = ρghS – масса жидкости в сосуде, ρ – плотность жидкости. Следовательно
Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда. Давление столба жидкости ρgh называют гидростатическим давлением.
Если жидкость находится в цилиндре под поршнем (рис. 1.15.2), то действуя на поршень некоторой внешней силой можно создавать в жидкости дополнительное давление p0 = F / S, где S – площадь поршня.
Таким образом, полное давление в жидкости на глубине h можно записать в виде:
Если на рис. 1.15.2 поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению: p0 = pатм.
| Рисунок 1.15.2. Зависимость давления от высоты столба жидкости |
Из-за разности давлений в жидкости на разных уровнях возникает выталкивающая или архимедова сила
Рис. 1.15.3 поясняет появление архимедовой силы. В жидкость погружено тело в виде прямоугольного параллелепипеда высотой h и площадью основания S. Разность давлений на нижнюю и верхнюю грани есть:
Поэтому выталкивающая сила будет направлена вверх, и ее модуль равен
FА = F2 – F1 = SΔp = ρgSh = ρgV,
где V – объем вытесненной телом жидкости, а ρV – ее масса.
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда, справедливо для тел любой формы.
| Рисунок 1.15.3. Архимедова сила. FА = F2 – F1 = S(p2 – p1) = ρgSh , F1 = p1S , F2 = p2S |
Из закона Архимеда вытекает, что если средняя плотность тела ρт больше плотности жидкости (или газа) ρ, тело будет опускаться на дно. Если же ρт < ρ, тело будет плавать на поверхности жидкости. Объем погруженной части тела будет таков, что вес вытесненной жидкости равен весу тела. Для подъема воздушного шара в воздухе его вес должен быть меньше веса вытесненного воздуха. Поэтому воздушные шары заполняют легкими газами (водородом, гелием) или нагретым воздухом.
Из выражения для полного давления в жидкости p = p0 + ρgh вытекает, что в сообщающихся сосудах любой формы, заполненных однородной жидкостью, давления в любой точке на одном и том же уровне одинаковы (рис. 1.15.4).
| Рисунок 1.15.4. Пример сообщающихся сосудов. В правом сосуде поверхность жидкости свободна. На уровне h давление в обоих сосудах одинаково и равно p0 = F / S = ρgh0 + pатм . Давление на дно сосудов p = p0 + ρgh |
Если оба вертикально расположенных цилиндра сообщающихся сосудов закрыть поршнями, то с помощью внешних сил, приложенных к поршням, в жидкости можно создать большое давление p, во много раз превышающее гидростатическое давление ρgh в любой точке системы. Тогда можно считать, что во всей системе устанавливается одинаковое давление p. Если поршни имеют разные площади S1 и S2, то на них со стороны жидкости действуют разные силы F1 = pS1 и F2 = pS2. Такие же по модулю, но противоположно направленные внешние силы должны быть приложены к поршням для удержания системы в равновесии. Таким образом,
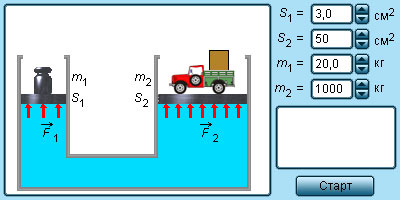
Если S2 >> S1, то F2 >> F1. Устройства такого рода называют гидравлическими машинами (рис. 1.15.5). Они позволяют получить значительный выигрыш в силе. Если поршень в узком цилиндре переместить вниз под действием внешней силы на расстояние то поршень в широком цилиндре переместится на расстояние поднимая тяжелый груз.
Таким образом, выигрыш в силе в раз обязательно сопровождается таким же проигрышем в расстоянии. При этом произведение силы на расстояние остается неизменным:
Это правило выполняется для любых идеальных машин, в которых не действуют силы трения. Оно называется «золотым правилом механики».
| Рисунок 1.15.5. Гидравлическая машина. |
Гидравлические машины, используемые для подъема грузов, называются домкратами. Они широко применяются также в качестве гидравлических прессов. В качестве жидкости обычно используются минеральные масла.
 |
Модель. Гидравлическая машина |
Источник
1. Значение давления столба жидкости
2. Эксперименты Паскаля
3. Гидростатический парадокс
Для понимания сути понятия «давление жидкости» нужно рассмотреть, что влияет на его формирование. Обычно рассматривают примеры по проще, а после переходят к изучению более сложных примеров. Гидростатическое давление в физике рассчитывается с учетом нескольких физических величин:
(p=ρgh) ,
где (p) – давление слоя жидкости, Па;
(ρ) – плотность жидкости, кг/м3;
(g) – ускорение свободного падения, м/с2;
(h) – высота столба жидкости, м.
Значение давления столба жидкости
Одной из величин, влияющих на давление жидкости, является высота столба жидкости, что находится в сосуде цилиндрической формы. Она обозначается буквой (h). Следует учесть, что для правильного определения давления жидкости сосуд должен иметь правильную форму – строго горизонтальное дно и вертикальные стенки. В такой ситуации давление жидкости в каждой точке сосуда будет одинаковым.
Для определения силы давления вводится понятие «площадь дна сосуда». При учете равного давления сила давления жидкости на дно сосуда рассчитается по формуле:
(F=ρghS).
Эта формула показывает, что сила давления соизмерима с весом жидкости, при условии использования сосуда правильной цилиндрической формы. Также доказано, что эти вычисления также применимы для расчета давления жидкости в сосудах самой разнообразной формы. Здесь действует правило, гласящее, что давление жидкости на дно сосуда равно во всех точках, при условии одинаковой высоты столба жидкости и площади дня сосуда. Но при этом реальный вес жидкости сосуда неровной формы может отличаться от ее силы давления. Он может быть больше либо меньше, но конечное значение, рассчитанное по вышеуказанной формуле, будет справедливым.
Эксперименты Паскаля
Паскаль был одним из первых ученых, кто изобрел базовые формулы для расчета гидростатического давления. Свои эксперименты он проводил при помощи установки, позже названной его именем. Основным отличием этого прибора было применение специальных подставок, на которых он фиксировал различные сосуды с жидкостями и производил расчеты. Сосуды были самой различной формы, благодаря чему эта установка стала прорывом в сфере исследования физических свойств жидкостей. Также на этом приборе представлялось возможным фиксирование сосуда без дна. При этом вместо него могла крепиться пластина. Она была расположена на одном из плечей коромысла весов.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Устанавливая и перемещая груз на противоположном конце коромысла ученый наполнял сосуд жидкостью. Во время возникновения силы давления жидкости, большей, чем вес груза, жидкость выливалась наружу через пластину. Измеряя высоту столба жидкости, Паскаль мог вычислить величину силы давления жидкости на дно сосуда. Он сравнивал эти значения с весом груза.
Он старался достичь большой силы давления при ограниченном количестве воды. Он просто увеличивал глубину столба жидкости. Еще Паскаль проводил испытания такого рода: к бочке, наполненной до краев и плотно закрытой крышкой, он присоединял длинную трубку, через которую добавлял воду. При повышении давления до определенного значения бочка не выдерживала и начинала протекать. И получалось так, что данный эффект достигался при малом объеме добавленной воды. Это значит, что именно высота трубки, иными словами, высота столба жидкости создавала разрушительное давление на дно бочки. Таким образом, к разрушению емкости привело критическое значение давления.
Также при изучении поведения жидкости Паскаль заметил, что наклон стенок сосуда играет важную роль при распределении давления. Имеют место излишки давления, направленного в разные стороны. Если сосуд сужается кверху, то давление будет действовать вверх. Подобный эксперимент можно провести самому, для этого нужна установка, подобная прибору Паскаля. Нужен поршень, переходящий в трубку, на котором статически крепится цилиндр. Трубка ставится вертикально, затем в нее заливается вода, при этом необходимо следить, чтобы объем над поршнем заполнялся равномерно, потом цилиндр нужно поднять вверх.
Можно сделать заключение, что давление является силой, что действует перпендикулярно на единицу площади. Давление измеряется в Паскалях (Па). Один Паскаль равняется силе воздействия в 1 Ньютон (Н), что действует на площадь, размером 1 м2.
Гидростатический парадокс
Гидростатический парадокс заключается в том, что давление жидкости не зависимо от ее объема и веса. Оно также не зависимо от формы сосуда, от размеров его дна, лишь только от высоты столба жидкости.
Не нашли что искали?
Просто напиши и мы поможем
Подобное явление называется парадоксом, так как оно противоречит привычным суждениям о физических свойствах жидкости. Опираясь на исследования Паскаля, можно утверждать, что давление жидкости зависит от ее плотности и глубины: (p=ρgh). Об этом гласит закон Паскаля: жидкость способна передавать давление во всех направлениях с одинаковой силой.
Гидростатическое давление возможно определить для любой точки объема жидкости, а также для стенок сосуда.
Источник
4.2. Элементы гидростатики
4.2.3. Гидростатическое давление
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление.
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
pгидр = ρ0gh,
где ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h – высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
Fгидр = pгидрS = ρ0ghS,
где pгидр – гидростатическое давление на дно сосуда; ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h – высота столба жидкости; S – площадь дна сосуда.
Рис. 4.10
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
p гидр = ρ 0 g h 2 ,
где ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h – высота вертикальной стенки сосуда (столба жидкости).
Рис. 4.11
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
F гидр = p гидр S = ρ 0 g h 2 S ,
где pгидр – гидростатическое давление на дно сосуда; ρж – плотность жидкости; g – модуль ускорения свободного падения; h – высота столба жидкости; S – площадь вертикальной стенки.
Рис. 4.11
При расчете давленияна днооткрытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
p = pатм + ρ0gh,
где pатм – атмосферное давление; ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h – глубина водоема.
Рис. 4.12
Сила давления на дно открытого водоема определяется произведением:
F = pS = (pатм + ρ0gh)S,
где S – площадь дна водоема.
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
p = ρ0gh1 cos α,
где ρ0 – плотность жидкости; g – модуль ускорения свободного падения; h1 – высота столба жидкости при вертикальном положении мензурки; h2 = h1 cos α – высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Рис. 4.13
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см3. Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение. Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
⟨ F гидр ⟩ = ⟨ p ⟩ S ,
где ⟨ p ⟩ – среднее гидростатическое давление на боковую поверхность цилиндра; S – площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
⟨ p ⟩ = ρ 0 g h 2 ,
где ρ0 – плотность жидкости, заполняющей сосуд; g – модуль ускорения свободного падения; h – высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
S = 2πRh,
где 2πr – длина окружности; R – радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая – периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления ⟨ p ⟩ и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
⟨ F гидр ⟩ = π ρ 0 g R h 2 .
Расчет дает значение:
⟨ F гидр ⟩ = π ⋅ 2,5 ⋅ 10 3 ⋅ 10 ⋅ 10 ⋅ 10 − 2 ⋅ ( 30 ⋅ 10 − 2 ) 2 ≈ 707 Н ≈ 0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см3. Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение. Давление в открытом водоеме определяется формулой
p = pатм + ρ0gh,
где pатм – атмосферное давление; ρ0 – плотность воды; g – модуль ускорения свободного падения; h – искомая глубина водоема.
По условию задачи
p = 4pатм.
Подстановка указанного значения в исходную формулу дает:
4pатм = pатм + ρ0gh,
или
3pатм = ρ0gh.
Выразим отсюда искомую глубину водоема
h = 3 p атм ρ 0 g
и произведем вычисление:
h = 3 ⋅ 100 ⋅ 10 3 1,0 ⋅ 10 3 ⋅ 10 = 30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
Гидростатическое давление
Рассмотрим равновесие однородной жидкости, находящейся в поле тяготения Земли.
На каждую частицу жидкости, находящейся в поле тяготения Земли, действует сила тяжести. Под действием этой силы каждый слой жидкости давит на расположенные под ним слои. В результате давление внутри жидкости на разных уровнях не будет одинаковым. Следовательно, в жидкостях существует давление, обусловленное ее весом.
Давление, обусловленное весом жидкости, называют гидростатическим давлением.
Для количественного расчета мысленно выделим в жидкости малый объем цилиндрической формы, расположенный вертикально, сечением S и высотой h (рис. 2). В случае неподвижной жидкости вес этого цилиндра, а значит, и сила давления на площадку S в основании будет равна силе тяжести (~m vec g).
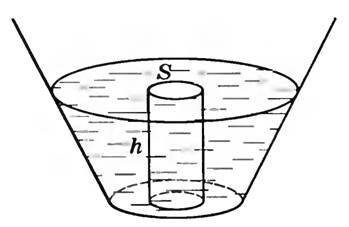
Рис. 2
Тогда давление на площадку
(~p = frac{mg}{S} = frac{rho Vg}{S} = frac{rho hSg}{S} = rho gh.)
(~p = rho gh) – гидростатическое давление, где ρ – плотность жидкости, h – высота столба жидкости. Таким образом, гидростатическое давление равно весу столба жидкости с единичным основанием и высотой, равной глубине погружения точки под свободной поверхностью жидкости.
Графически зависимость давления от глубины погружения в жидкость представлена на рисунке 3.
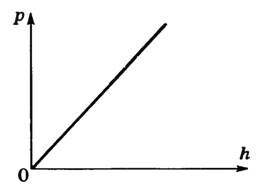
Рис. 3
Давление жидкости на дно не зависит от формы сосуда, а определяется только высотой уровня жидкости и ее плотностью. Во всех случаях, приведенных на рисунке 4, давление жидкости на дно сосудов одинаково.
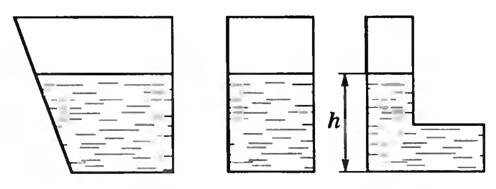
Рис. 4
Жидкость давит на данной глубине одинаково по всем направлениям – не только вниз, но и вверх, и в стороны.
Следовательно, давление на стенку на данной глубине будет таким же, как и давление на горизонтальную площадку, расположенную на той же глубине.
Если над свободной поверхностью жидкости создается давление p0 то давление в жидкости на глубине будет
(~p = p_0 + rho gh.)
Обратите внимание на различие выражений: “давление жидкости на глубине h” (p = pgh) и “давление в жидкости на глубине h” (p = p0 + pgh). Это надо учитывать при решении различных задач.
Силы давления на дно и на стенки можно рассчитать по формулам[~F_d = rho gh S_d] – сила давления жидкости на горизонтальное дно, где Sd – площадь дна;
(~F_{st} = frac{rho gh}{2} S_{st}) – сила давления жидкости на боковую прямоугольную вертикальную стенку сосуда, где Sst – площадь стенки.
В покоящейся жидкости свободная поверхность жидкости всегда горизонтальна.
Нередко встречаются случаи, когда жидкость, покоясь относительно сосуда, движется вместе с ним. Если при этом сосуд движется равномерно и прямолинейно, то свободная поверхность жидкости будет горизонтальна. Но если сосуд движется с ускорением, то ситуация меняется и возникают вопросы о форме свободной поверхности жидкости, о распределении давления в ней.
Так, в случае горизонтального движения сосуда с ускорением (~vec a) в поле тяготения Земли любая часть жидкости массой m движется с тем же ускорением (~vec a) под действием равнодействующей силы давления (~vec N_d), действующей со стороны остальной жидкости и силы тяжести (~m vec g) (рис. 5).
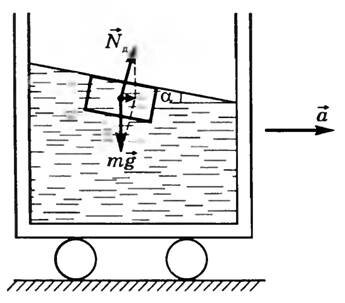
Рис. 5
Основное уравнение динамики:
(~vec N_d + m vec g = m vec a.)
В результате свободная поверхность жидкости не будет горизонтальна, а образует с горизонтом угол α, который можно легко найти, если спроецировать а основное уравнение динамики на горизонтальную и вертикальную оси[~N_d sin alpha = ma; N_d cos alpha = mg]. Отсюда
(~operatorname{tg} = frac ag.)
Давление на горизонтальную поверхность (горизонтальное дно) будет возрастать в направлении, противоположном ускорению.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. – Мн.: Адукацыя i выхаванне, 2004. – C. 95-97.
Источник
