Давление жидкости на дно сосуда калькулятор
Random converter
- Калькуляторы
- Гидравлика и гидромеханика — жидкости
Калькулятор гидростатического давления

Этот калькулятор гидростатического давления определяет гидростатическое давление, действующее на тело, находящееся в жидкости на определенной глубине.
Пример: Рассчитать давление, действующее на аквалангиста на глубине 15 м. Плотность морской воды 1022 кг/м³ и атмосферное давление 101325 Па.
Плотность жидкости
ρ
Глубина или высота столба жидкости
h
Внешнее давление
P
Ускорение силы тяжести
gм/с²
Поделиться ссылкой на этот калькулятор, включая входные параметры
Выходные данные
Гидростатическое давление
P Па
Для расчета введите единицы и нажмите кнопку Рассчитать.
Определения и формулы
Гидростатика — раздел физики, изучающий жидкости в состоянии равновесия, в частности, при воздействии на них гравитационного поля. В отличие от гидродинамики, изучающей движение жидкостей и силы, действующие на твердые тела, погруженные в движущиеся жидкости, гидростатика изучает механические свойства и поведение жидкостей в покое, в устойчивом равновесии. Гидростатика, в частности, изучает давление, оказываемое несжимаемыми жидкостями на погруженные в них тела.
Гидростатика широко применяется в метеорологии, медицине (изучение давления в кровеносных сосудах), биологии, инженерном деле, например, при разработке оборудования для использования и транспортировки жидкостей или при проектировании плотин. Гидростатика объясняет многие явления, встречающиеся в повседневной жизни, например, почему предметы могут плавать или тонуть в воде или почему поверхность спокойной воды горизонтальна и перпендикулярна направлению силы тяжести.
Гидростатическое давление — давление вследствие силы тяжести находящейся в равновесии жидкости в любой точке внутри этой жидкости. Оно увеличивается пропорционально глубине жидкости, так как чем глубже погружено тело в воде, тем больше жидкости вес жидкости, который действует на ту же поверхность (подробнее о давлении — в наших калькуляторе давления and конвертере давления). Гидростатическое давление определяется приведенной ниже формулой, называемым основным уравнением гидростатики, которая и используется в нашем калькуляторе:

где P — гидростатическое давление, измеряемое в системе СИ в паскалях (Па), ρ — плотности жидкости, измеряемая в килограммах на кубический метр (кг/м³), P0 — внешнее давление, измеряемое в паскалях, которое обычно является атмосферным давлением (P0 = 101325 Па), g ускорение свободного падения, измеряемое в метрах в секунду за секунду (м/с²), и h — глубина жидкости, измеряемая в метрах (м).
Значение h может также относиться к высоте и это уравнение можно использовать для определения давления столба жидкости указанной высоты.
Отметим, что это уравнение не содержит общей массы или объема жидкости, так как давление не зависит от формы сосуда, массы жидкости или ее полного объема — давление на любой глубине остается одинаковым при любой форме сосуда, в который налита жидкость.
При погружении на аквалангиста или водолаза действует гидростатическое давление, которое имеется на данной глубине. Это давление зависит от глубины погружения и увеличивается на 1 бар на каждые 10 метров (33 фута) погружения. Из-за действия этого давления воздух в полостях тела сжимается при увеличении глубины погружения. Это одна из причин, из-за которых аквалангист должен выравнивать давление в ушах путем добавления воздуха через нос в маску. Аквалангист также должен избегать быстрого неконтролируемого всплытия.
Основные свойства жидкостей были независимо открыты французским математиком, физиком и изобретателем Блезом Паскалем (1623–1662) и голландским математиком Симоном Стевином (1584-1620) и основное уравнение гидростатики в англоязычной литературе иногда называют законом Стевина. Следует отметить, что Стевин определил величину гидростатического давления до Паскаля, однако Паскаль не знал голландского и работ Стевина не читал.
Поскольку в результате наличия гравитационного поля на погруженные в жидкость тела действует гидростатическое давление, на все погруженные в жидкость тела действует также выталкивающая сила. Закон, определяющий выталкивающую силу, действующую на полностью или частично погруженные в жидкость плавающие предметы, был открыт Архимедом, который большую часть жизни прожил в Сиракузах на Сицилии. Он предположил, что эта сила равна весу жидкости, вытесненной телом.
В связи с высоким давлением под водой и необходимостью медленного всплытия, водолазы могут работать, например, на глубине 35 м всего 30 минут. Для увеличения рабочего времени используется метод длительного пребывания под давлением в режиме насыщения. Он позволяет водолазам дольше работать на больших глубинах без риска возникновения декомпрессионной (кессонной) болезни. При использовании этого метода водолазы живут в жилых барокамерах на поверхности или под водой. Из жилой барокамеры водолазов перемещают под воду в место выполнения работ и обратно в закрытом водолазном колоколе, называемом также капсулой для транспортировки персонала (англ. personnel transfer capsule). Капсула представляет собой усовершенствованный водолазных колокол в форме цилиндра (показанного на фотографии) или сферы, который вмещает двух или трех человек. На наружной стороне капсулы установлены баллоны для хранения дыхательной смеси.
Капсула для транспортировки персонала (3 человека), которую использовали при строительстве висячего моста Акаси-Кайкё, соединяющего город Кобе в Японии с островом Авадзи.
Гидравлика и гидромеханика — жидкости
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Источник
Определение гидростатического давления
Определение
Физическая величина, равная отношению нормальной силы ($F$), действующей со стороны жидкости на некоторую площадь,
на величину этой площади ($S$) называют давлением ($p$) жидкости:
[p=frac{F}{S}left(1right).]
Если несжимаемая жидкость находится в равновесии давление по горизонтали всегда одно и то же. Свободная поверхность жидкости всегда горизонтальна, за исключением места около стенок сосуда. У несжимаемой жидкости плотность не зависит от давления. Если поперечное сечение цилиндрического столба жидкости равно $S$, высота столба $h$, плотность жидкости $rho $, тогда вес ($P$) этого столба равен:
[P=rho gSh left(2right).]
В соответствии с (1) давление на основание столба жидкости составит величину:
[p=frac{P}{S}=rho ghleft(3right).]
Формула (3) указывает, что давление столба несжимаемой жидкости на дно сосуда зависит от высоты и плотности жидкости.
В общем случае плотность зависит от температуры жидкости. Давление, которое вычисляется при помощи формулы (3)
называют гидростатическим давлением/
Определение
И так, гидростатическим давлением называют давление столба жидкости, находящейся в состоянии равновесия, над некоторым
условно выбранным уровнем при действии силы тяжести. Гидростатическое давление определяется по формуле (3).
Давление внутри жидкости ($p$) на глубине $h$, будет складываться из давления атмосферы ($p_0$) и гидростатического давления:
[p=p_0+rho ghleft(4right).]
Единицей измерения гидростатического давления в Международной системе единиц (СИ) является паскаль (Па):
[left[pright]=Па=frac{кг}{с^2cdot м}.]
Закон Архимеда
В соответствии с формулой (3) давление, оказываемое на нижние слои жидкости больше, чем на верхние. Из-за этого тело, погруженное в жидкость, испытывает действие выталкивающей силы. Величину выталкивающей силы определяет закон Архимеда: На тело, находящееся в жидкости (газе) действует выталкивающая сила, которая равна весу жидкости (газа) вытесненной телом. Эта сила называется силой Архимеда ($F_A$):
[F_A=rho gV left(4right),]
где $V$ – объем тела; $rho $ – плотность жидкости; $g$ – ускорение свободного падения. Сила Архимеда направлена вверх.
Примеры задач с гидростатическим давлением
Пример 1
Задание. В чем состоит суть гидростатического парадокса?
Решение. Гидростатическим парадоксом называют явление, при котором сила весового давления жидкости, находящейся в сосуде отличается от веса находящейся там жидкости. Сила давления жидкости на дно емкости равняется весу жидкости только в том случае, если сосуд имеет форму цилиндра. При такой конфигурации емкости стенки являются вертикальными, силы давления стенок на жидкость (соответственно, жидкости на стенки) направлены горизонтально, вертикальной составляющей они не имеют (рис.1).
Если сосуд имеет вверху поперечное сечение больше, чем сечение дна, то сила давления на дно меньше, чем вес жидкости. И наоборот, если сосуд с жидкостью имеет сужающееся вверху горло, то сила давления на дно сосуда больше, чем вес жидкости. Причиной возникновения гидростатического парадокса является то, что жидкость оказывает давление не только на дно сосуда, но давит и на его стенки. При этом давление на стенки сосуда, расположенные не перпендикулярно основанию имеют вертикальную составляющую. При этом в сосуде, который расширяется к верху, эта составляющая направлена вверх, а в сосуде, уменьшающем свое сечение к верху, вертикальная составляющая давления направлена вниз. Вес жидкости вычисляется как сумма всех вертикальных компонент давления жидкости по внутренней площади емкости.
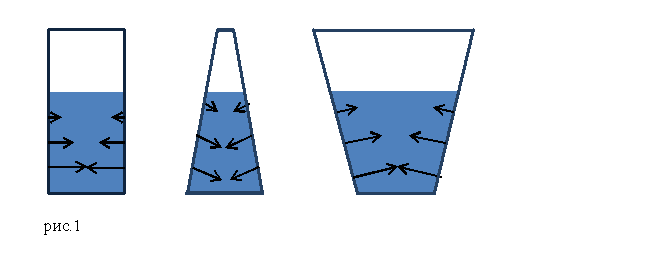
Пример 2
Задание. Каково гидростатическое давление воды на дно сосуда с водой, если высота столба жидкости составляет $h=$0,5 м?
Решение. Гидростатическое давление на дно сосуда найдем как:
[p=rho gh left(2.1right),]
где $rho =1000 frac{кг}{м^3}$.
Вычислим это давление:
[p=1000cdot 9,8cdot 0,5approx 5000 (Па)]
Ответ. $papprox 5000$ Па
Читать дальше: движение по окружности.
Источник
Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.
Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòàòè÷åñêèì.
Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:
1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:
2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
F=mg. (1.28)
Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:
m = pV, (1.29)
à îáúåì — ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:
V=Sh. (1.30)
Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:
F = pVg=pShg. (1.31)
Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:
pS = pSkg.
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:
p = phg.
Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.
Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàêæå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ — ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.
 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.
Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæàþùèõñÿ — áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñóäîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S — ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ — ñïîñîáíîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.
Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëåíèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâøèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëåíèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Источник
Random converter
- Калькуляторы
- Механика
Калькулятор давления

Этот калькулятор давления определяет давление по известной силе, приложенной перпендикулярно к поверхности с известной площадью.
Пример: Девушка весом 50 кг в туфлях на высоких каблуках во время ходьбы кратковременно касается пола одним каблуком. Каково давления каблука на пол в момент касания, если площадь каблука 2 cm².
Площадь
A
Сила
F
Давление
P
Поделиться ссылкой на этот калькулятор, включая входные параметры
Для расчета введите любые две величины из трех, выберите единицы измерения и нажмите кнопку Рассчитать.
Определения и формулы
Давление на поверхность определяется как сила, действующая на поверхность объекта перпендикулярно этой поверхности. Иными словами, давление определяется как сила, действующая на единицу площади, по которой распределяется действие этой силы. В СИ давление измеряется в паскалях (Па) или ньютонах на квадратный метр (Н/м²). В традиционных британских и американских единицах давление измеряется в фунтах на квадратный дюйм (англ. сокращение PSI). Давление, силу и площадь можно конвертировать из одних единиц в другие с помощью Конвертера единиц давления, Конвертера единиц площади и Конвертера единиц силы.
Измерение давления шин в игрушечном автомобиле
Другим видом давления является гидростатическое давление, то есть давление жидкости, передаваемое одинаково во все стороны в жидкости или газе, находящемся в сосуде. В сосуде, в котором жидкость находится в покое, давление в любой точке одинаковое.
Имеется также звуковое или акустическое давление, которое представляет собой отклонение от атмосферного давления окружающей среды при прохождении через нее звуковой волны, действующей на поверхность перпендикулярно направлению ее движения.
При ежедневных измерениях давления, например, при проверке давления в шинах автомобиля, оно измеряется относительно давления окружающего воздуха. Такое давление называется манометрическим или избыточным и представляет собой разность между абсолютным и атмосферным давлением. Цифровые манометры измеряют давление с помощью связанных с мембраной тензометрических датчиков, сообщающихся с атмосферой. Такие манометры показывают нуль, если их штуцер сообщается с атмосферой.
Основная формула для давления имеет вид:

где P — давление и F is the force generated by a load acting on a surface with area A.
Давление измеряется манометрами. За почти 400 лет с момента изобретения Эванджелистой Торричелли первого манометра, было изобретено множество разновидностей этих приборов для измерения давления. Все они имеют различные преимущества и недостатки и отличаются различной чувствительностью, диапазоном измерения и типами среды, давление которой они измеряют. Для изучающих английский язык стоит отметить, что, в отличие от русского языка, английский термин manometer относится только к ртутному манометру, хотя иногда и используется для других типов манометров. Остальные манометры по-английски называются pressure gauges.
Поток воды, вырывающийся с большой скоростью из поврежденной водопроводной магистрали, в которой вода находится под высоким давлением
Давление газов и жидкостей обычно измеряется манометрами поршневого и анероидного типа. Манометры жидкостного типа, в которых жидкость, например, вода или ртуть, находится в трубке, концы которой подвергаются действию разных давлений, применяются достаточно редко.
В поршневом манометре имеется поршень, который перемещается в цилиндре под действием давления среды, действующего на одну сторону поршня. С другой стороны поршня находится пружина.
В манометре анероидного типа (также называемом механическом манометром) основным элементом является металлическая коробка, которая изменяет форму под действием давления. Такой элемент может иметь форму гофрированной коробки или плоской металлической трубки, изогнутой в дугу. Трубка стремится распрямиться и возвращается к исходной форме, когда давление снимается.
Артериальное давление традиционно измерялось ртутными сфигмоманометрами и позже механическими манометрами. В последнее время артериальное давление измеряют электронными приборами, в которых в качестве датчиков используются тензометрические датчики пьезоэлектрического или тонкопленочного типа.
Акустическое давление обычно измеряют с помощью измерительного микрофона (в воздухе) или измерительного гидрофона (в воде).
Детали механического манометра: 1 — стационарный конец трубки Бурдона, 2 — приемный штуцер, 3 — рычаг с секторной шестерней, 4 — звено, приводящее в движение секторную шестерню, 5 — секторная шестерня, приводящая в движение зубчатое колесо (трибку), связанное со стрелкой, 6 — подвижный конец трубки Бурдона, 7 — стрелка манометра, 8 — пружина, предотвращающая свободный ход механизма перемещения стрелки.
Механика
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Источник
