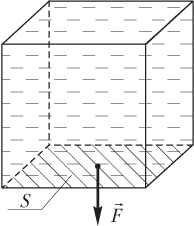
Давление жидкости на площадь стенки сосуда
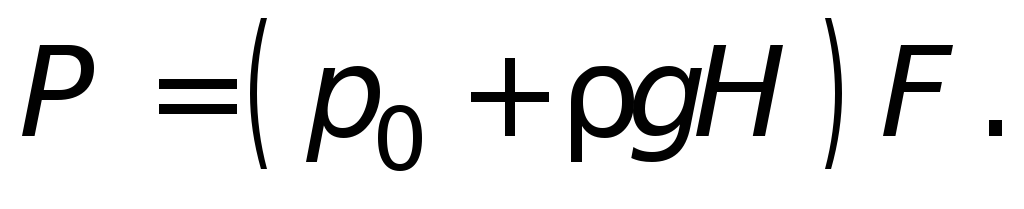
Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.
Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòàòè÷åñêèì.
Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:
1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:
2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
F=mg. (1.28)
Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:
m = pV, (1.29)
à îáúåì — ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:
V=Sh. (1.30)
Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:
F = pVg=pShg. (1.31)
Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:
pS = pSkg.
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:
p = phg.
Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.
Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàêæå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ — ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.
 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.
Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæàþùèõñÿ — áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñóäîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S — ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ — ñïîñîáíîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.
Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëåíèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâøèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëåíèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Источник
Что это такое?
В сосуде, заполненном водой, на дно давит сила, равная весу столба жидкости. Это вызванное силой тяжести давление называется гидростатическим.
Оно определяется отношением силы к площади, то есть его физический смысл – это сила, действующая на единицу площади (см2).
 Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Законы гидростатики описал Блез Паскаль. В 1648 г. он удивил горожан опытом, демонстрирующим свойства воды.
Вставив в бочку, заполненную водой, длинную узкую трубку, он налил в нее несколько кружек воды, и бочку разорвало.
Согласно закону Паскаля, приложенное к H2O усилие распространяется равномерно во всем объеме. Это объясняется тем, что вода почти не сжимается. В гидравлических прессах используют это свойство.
Плотность воды все же растет при высоком давлении. Это учитывается при расчетах конструкций глубоководных аппаратов.
Факторы, влияющие на показатель
При отсутствии внешнего воздействия, играют роль два фактора:
- высота столба;
- плотность.
Выше уровень воды, налитой в сосуд, — выше напор на дно. Если в одной емкости ртуть, а в другой вода и при этом уровни жидкостей одинаковы, то в первом случае давление на дно больше, так как ртуть имеет большую плотность.
Сверху на содержимое сосуда давит также атмосферный воздух. Поэтому в сообщающихся сосудах уровень одинаков, ведь в каждом из них над поверхностью атмосфера одна и та же.
Если же к поверхности приложить поршень и давить на него, то напор будет складываться из:
- внешней силы;
- веса воды.
При этом форма сосуда не определяет размер усилия, создаваемого столбом. Оно будет одним и тем же при равной высоте столба, хотя стенки емкости могут расширяться кверху или сужаться.

На дно и стенку сосуда – в чем разница?
Вода, заполняющая емкость, оказывает давление по направлению всегда перпендикулярно поверхности твердого тела, по всей площади соприкосновения с дном и стенками.
Усилие на дно распределено равномерно, то есть оно одинаково в любой точке. Заполнив водой сито, можно увидеть, что струи, текущие через отверстия, равны по напору.
Наполнив сосуд, имеющий отверстия одного диаметра в стенках на разной высоте, можно наблюдать различный напор вытекающей струи. Чем выше отверстие – тем слабее струя. То есть, давление на стенки емкости тем больше, чем ближе ко дну.
Единицы измерения
 Давление воды измеряют в:
Давление воды измеряют в:
- паскалях – Па;
- метрах водяного столба – м. в. ст.
- атмосферах – атм.
Практически достаточно знать, что 1 атмосфера равна 10 метрам водяного столба или 100000 Па (100кПа).
Формулы расчета
Давление на дно сосуда рассчитывается делением силы на площадь, то есть оно равно произведению плотности воды, высоты столба и ускорения свободного падения g (величина постоянная, равна 9,8 м/с2).
Пример расчета: бак наполнен водой (плотность 1000 кг/м3) до высоты 1,2 м. Нужно найти, какое давление испытывает дно бака. Решение: P = 1000*1, 2*9, 8 = 11760 Па, или 11, 76 кПа.
Для расчета давления на стенки сосуда применяют все ту же формулу напора, приведенную выше. При расчете берется глубина от точки, в которой нужно рассчитать напор, до поверхности воды.
Пример расчета: на глубине 5 м на стенку резервуара с водой будет оказываться давление P=1000 *5 * 9, 8=49000 кПа, что составляет 0,5 атмосферы.
Расчет давления воды на дно и стенки сосуда в видео:
Применение на практике
Примеры использования знаний свойств воды:
-
 Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм.
Подбирая насос для водоснабжения дома высотой 10 м, понимают, что напор должен быть минимум 1 атм. - Водонапорная башня снабжает водой дома ниже ее по высоте, напор в кране у потребителей обеспечен весом столба воды в баке.
- Если в стенках бочки появились отверстия, то, чем ниже они расположены, тем более прочным должен быть материал для их заделки.
- Замеряют дома напор холодной воды в кране манометром. Если он менее чем 0,3 атм (установлено санитарными нормами), есть основания для претензий к коммунальщикам.
Используя гидравлический пресс, можно получить большое усилие, при этом приложив малую силу. Примеры применения:
- выжимка масла из семян растений;
- спуск на воду со стапелей построенного судна;
- ковка и штамповка деталей;
- домкраты для подъема грузов.
Заключение
Такие свойства воды, как текучесть и несжимаемость, дают возможность использовать силу ее давления для самых различных целей.
Опасность этого явления учитывают при расчетах на прочность корпусов подводных лодок, стенок и днищ резервуаров, в которых хранят воду. Сила давления воды совершает полезную работу, она же способна и разрушать.
А какова Ваша оценка данной статье?
Источник
При расчете резервуаров и различных емкостей для хранения жидкостей требуется знать полное давление жидкости на ограничивающие ее твердые стенки и точку приложения равнодействующей сил давления. Пусть задана плоская вертикальная стенка АВ (рис. 1.9).
Гидростатическое давление жидкости на всей площади поверхности стенки складывается из суммы гидростатических давлений во всех ее точках и называется суммарным давлением жидкости. Для определения этого давления необходимо установить, как оно распределяется по поверхности тела, на которое воздей-

Рис. 1.9. К определению силы гидростатического давления на плоскую поверхность:
а — эпюра гидростатического давления; б — положение центров тяжести и давления на плоской прямоугольной стенке
ствует жидкость. Графическое изображение распределения давления по высоте тела, например стенки, называется эпюрой гидростатического давления (см. рис. 1.9, а).
Гидростатическое давление в точке жидкости, расположенной на любой глубине от свободной поверхности, может быть определено по формуле (1.21)

Поверхностное давление в открытом сосуде, равное атмосферному давлению р0 = /?атм, передается в любую точку жидкости без изменения и является постоянным. Избыточное гидростатическое давление рgh пропорционально глубине погружения точки, т. е. изменение его значения по глубине подчинено линейному закону.
Атмосферное давление ратм, действующее на свободную поверхность жидкости и полностью передающееся в любую точку на стенке внутри жидкости, уравновешивается таким же атмосферным давлением, действующим снаружи на стенку сосуда. Поэтому при расчете стенок на прочность и устойчивость определяют и учитывают только избыточное давление р = рgh.
Эпюра избыточного гидростатического давления на вертикальную стенку сосуда приведена на рис. 1.9, а. Избыточное давление в точке А равно р = 0 (/? = 0), а в точке В — р = рgh.
В каждой точке жидкости давление нормально к поверхности стенки, поэтому на нормали к точке В откладываем в принятом масштабе отрезок BE, равный рgh, и соединяем прямой с точкой А. Треугольник АВЕ показывает распределение избыточного гидростатического давления по высоте стенки.
Каждая ордината этого треугольника представляет собой избыточное давление в соответствующей точке стенки, а площадь треугольника — силу суммарного избыточного давления жидкости на стенку в перпендикулярной ей плоскости. Если эту площадь умножить на ширину стенки Ь, то получим силу гидростатического давления, действующую на стенку сосуда:

Однако = hc, hb = F, следовательно

где F — площадь стенки, находящейся под поверхностью жидкости; hc — глубина погружения центра тяжести плоской поверхности (точка Сна рис. 1.9).
Сила избыточного давления, оказываемая на плоскую стенку, находящуюся под воздействием жидкости, равна произведению площади смоченной поверхности стенки на избыточное гидростатическое давление в ее центре тяжести. Это правило распространяется и на полное суммарное давление, и на любую плоскую фигуру, погруженную в жидкость. При учете поверхностного давления абсолютное суммарное давление, действующее на стенку, расчитывается по формуле:

Полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление рс в центре тяжести этой площади. Формула (1.28) справедлива и для любой наклонной плоскости с произвольными очертаниями.

Рис. 1.10. Гидростатический парадокс
Если стенка расположена горизонтально, т. е. является горизонтальным дном сосуда, то полная сила давления на дно Ран определяется по формулам

где h — высота столба жидкости над дном; F — площадь дна.
Сила давления на дно Рт зависит лишь от плотности жидкости, высоты столба жидкости и площади дна и не зависит от формы дна и объема сосуда, т. е. для сосудов разной формы давление на дно будет одинаковым, если они имеют одинаковую площадь дна и наполнены одинаковой жидкостью до одного и того же уровня. Это явление называется гидростатическим парадоксом, (рис. 1.10).
Точка приложения равнодействующей силы давления на стенку называется центром давления. Центр давления расположен ниже центра тяжести (точки С) (см. рис. 1.9). Только на горизонтальной стенке (дно сосуда) центр давления совпадает с центром тяжести. Положение центра давления легко определять графически. Равнодействующая сила давления проходит через центр тяжести эпюры. Проекция этого центра на плоскость стенки и есть центр давления. Для прямоугольной стенки равнодействующая силы гидростатического давления и центр давления находятся на расстоянии /?/3 от основания или 2/3/? от поверхности жидкости.
Координата центра давления yD, т. е. расстояние от свободной поверхности жидкости до центра давления, измеряемое вдоль стенки, может быть определена по формуле

где ус — расстояние от центра тяжести площади смоченной поверхности стенки до свободной поверхности жидкости, измеряемое вдоль стенки; /0 — момент инерции площади смоченной поверхности стенки относительно оси, проходящей через ее центр тяжести; F — площадь смоченной поверхности стенки.
Источник
4.2. Элементы гидростатики
4.2.3. Гидростатическое давление
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление.
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
pгидр = ρ0gh,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
Fгидр = pгидрS = ρ0ghS,
где pгидр — гидростатическое давление на дно сосуда; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь дна сосуда.
Рис. 4.10
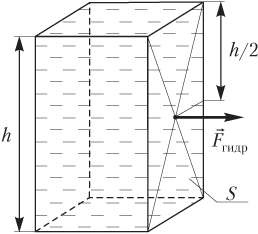
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
pгидр=ρ0gh2,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
Рис. 4.11
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
Fгидр=pгидрS=ρ0gh2S,
где pгидр — гидростатическое давление на дно сосуда; ρж — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь вертикальной стенки.
Рис. 4.11
При расчете давленияна днооткрытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — глубина водоема.
Рис. 4.12
Сила давления на дно открытого водоема определяется произведением:
F = pS = (pатм + ρ0gh)S,
где S — площадь дна водоема.
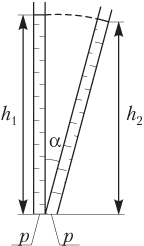
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
p = ρ0gh1 cos α,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h1 — высота столба жидкости при вертикальном положении мензурки; h2 = h1 cos α — высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Рис. 4.13
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см3. Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение. Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
〈Fгидр〉=〈p〉S,
где 〈p〉 — среднее гидростатическое давление на боковую поверхность цилиндра; S — площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
〈p〉=ρ0gh2,
где ρ0 — плотность жидкости, заполняющей сосуд; g — модуль ускорения свободного падения; h — высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
S = 2πRh,
где 2πr — длина окружности; R — радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая — периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления 〈p〉 и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
〈Fгидр〉=πρ0gRh2.
Расчет дает значение:
〈Fгидр〉=π⋅2,5⋅103⋅10⋅10⋅10−2⋅(30⋅10−2)2≈707 Н≈0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см3. Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение. Давление в открытом водоеме определяется формулой
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — искомая глубина водоема.
По условию задачи
p = 4pатм.
Подстановка указанного значения в исходную формулу дает:
4pатм = pатм + ρ0gh,
или
3pатм = ρ0gh.
Выразим отсюда искомую глубину водоема
h=3pатмρ0g
и произведем вычисление:
h=3⋅100⋅1031,0⋅103⋅10=30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
Формула давления на дно и стенки сосуда
Давление жидкости обусловлено ее весом и, соответственно сила этого давления F равна весу жидкости P. Вес жидкости можно определить, зная ее массу m. А массу можно вычислить по формуле: m=ρV. Объем жидкости в прямоугольном сосуде легко рассчитать. Обозначим высоту сосуда h, а площадь дна буквой S. Тогда объем будет равен: V=Sh. Формула массы в таком случае принимает вид: m=ρV=ρSh . Вес жидкости будет равен: P=gm=gρSh. чтобы рассчитать давление, нам нужна сила этого давления. А мы уже говорили, что сила давления в данном случае равна весу жидкости, поэтому формула давления принимает следующий вид:
Формула для этого давления в атмосфере. Кроме того, поскольку давление представляет собой силу на единицу измерения площади, то. Чтобы рассчитать давление через инструмент барометра, можно было бы заменить объем ртути в барометре в уравнение. Это дало бы уравнение. Вероятно, метеоролог даст атмосферное давление или барометрическое давление в 30 дюймов. Он состоит из длинной трубки, закрытой на одном конце, заполненной ртутью и перевернутой в сосуде с ртутью. На уровне моря сила атмосферного давления будет поддерживать колонку с содержанием ртути 760 мм в высоту.
p=P/S=gρSh/S или p=gρh
То есть в итоге мы пришли к очень интересному моменту – давление не зависит от объема и формы сосуда. Оно зависит только от плотности и высоты столба конкретной жидкости в данном случае. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
Для давления газа на дно и стенки сосуда формула будет иметь точно такой же вид.
Простые приложения, связанные с давлением
Фактически вес столба ртути равен силе атмосферного давления. Подобным же образом атмосферное давление заставляет воду в подобной колонне высотой до 34 футов! После запуска атмосферное давление на поверхность верхнего контейнера заставляет воду за короткую трубу заменить воду, вытекающую из длинной трубки.
- Фактически это приводит к снижению давления воздуха внутри соломы.
- Сифон можно запустить, заполнив трубку водой.
Наблюдения Бойля можно суммировать в утверждении: при постоянной температуре объем газа изменяется обратно пропорционально давлению, оказываемому на него.
Применение давления на дно и стенки сосуда
Еще один интересный момент заключается в том, что согласно закону Паскаля давление распределяется равномерно не только на дно и стенки, но и в направлении вверх. То есть, если мы погрузим какое-либо тело на определенную глубину, то на него снизу будет действовать сила, равная силе давления на данной глубине, как бы выталкивая тело на поверхность. Именно благодаря этому явлению возможно плавание кораблей. Несмотря на довольно внушительный вес, вода выталкивает судно вследствие эффекта давления воды на стенки сосуда, которыми в данном случае являются борта корабля. С понижением глубины давление увеличивается. Люди научились использовать это явление
, делая борта кораблей в форме сужающихся вниз конусов. Именно поэтому нас доступно покорение морей и океанов.
Кинетическая молекулярная теория Пояснение
Наблюдения за давлением можно объяснить, используя следующие идеи. Быстрое движение и столкновения молекул со стенками контейнера вызывает давление. Давление пропорционально числу молекулярных столкновений и силе столкновений в определенной области. Чем больше столкновений молекул газа со стенками, тем выше давление.
В 17 веке Роберт Бойл впервые сформулировал связь между давлением, объемом и температурой, поскольку они связаны с газом по формуле. Эта формула была результатом его экспериментов с газом, и, как он заметил, газ имел тенденцию к изменению давления, когда он занимал контейнеры различного размера.
А что по поводу давления газов?
Что касается газов, то для них расчет будет абсолютно таким же. Соответственно, наибольший вес окружающего нас газа – воздуха, будет у поверхности Земли. А с увеличением высоты будет уменьшаться как среднее давление, так и плотность окружающего газа. Поэтому воздух на высоте очень разреженный. Там очень трудно как дышать, так и летать, потому что крыльям самолетов не на что опираться. Именно поэтому набирать очень большую высоту летательные аппараты могут только на очень высокой скорости, увеличивая таким образом количество воздуха под крылом в единицу времени.
Эта связь часто упоминается как Закон Бойля. Кроме того, Бойл отметил, что газы имеют тенденцию «возвращаться» к его первоначальному давлению после удаления из контейнера, в котором он либо был сжат, либо расширен. Общая разница в высоте напрямую коррелировала с давлением атмосферы.
Бойл проиллюстрировал это через формула. Рон Куртус. Давление – это сила на объекте, который распространяется по поверхности. Уравнение для давления – это сила, деленная на область, где применяется сила. Хотя это измерение является простым, когда твердое тело надавливает на твердое тело, корпус твердого тела, нажимая на жидкость или газ, требует, чтобы жидкость была ограничена в контейнере.
Нужна помощь в учебе?
Предыдущая тема: Давление в жидкости и газе
Следующая тема:   Сообщающиеся сосуды
В соответствии с законом Паскаля
гидростатическое давление на уровне
горизонтального дна сосуда при высоте
жидкости в сосуде, равной Н
,
Сила также может быть создана весом объекта. Вопросы, которые могут возникнуть, включают.
- Какое давление, когда твердое тело подталкивает другое твердое тело?
- Что происходит, когда твердое тело нажимает на ограниченную жидкость?
- Что происходит, когда сила исходит из гравитации?
Этот урок ответит на эти вопросы.
Когда вы применяете силу к твердому объекту, давление определяется как прилагаемое усилие, деленное на область применения. Вы можете видеть, что при заданной силе, если площадь поверхности меньше, давление будет больше. Если вы используете большую область, вы распространяете силу, и давление становится меньше.
Отсюда следует, что абсолютное давление
р
на горизонтальное дно не зависит
от формы сосуда и объема жидкости в нем.
При данной плотности жидкости оно
определяется лишь высотой столба
жидкостиН
и внешним давлениемр
0 .
Сила давления жидкости Р
ж на
дно сосуда зависит от его площадиF
:
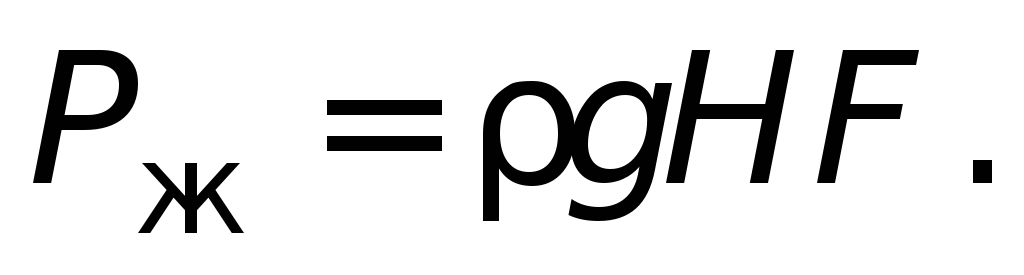 (1.8)
(1.8)
Твердое прессование на ограниченной жидкости
Когда жидкость или газ заключены в контейнер или цилиндр, вы можете создать давление, применяя усилие с помощью твердого поршня. В ограниченной жидкости – пренебрегая влиянием силы тяжести на жидкость – давление одинаково во всем контейнере, одинаково нажимая на все стенки. В случае велосипедного насоса давление, создаваемое внутри насоса, будет передаваться через шланг в велосипедную шину. Но воздух все еще ограничен.
Увеличение силы увеличит давление внутри цилиндра. Поскольку вес объекта является силой, вызванной гравитацией, мы можем заменить вес в уравнении давления. Таким образом, давление, вызванное весом объекта, – это вес, разделенный на область, где применяется вес.
Общая сила давления на дно сосуда
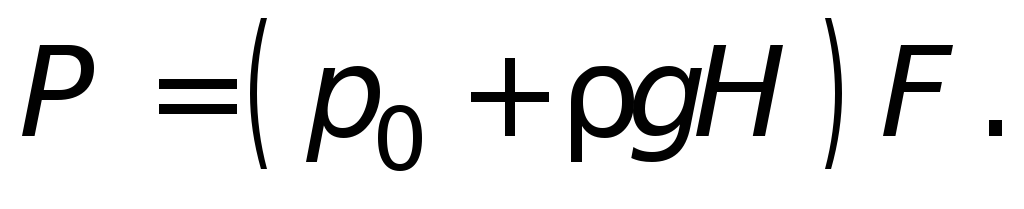 (1.9)
(1.9)
Внешнее давление р 0 передается
жидкостью каждому элементу поверхности
стенки одинаково, поэтому равнодействующая
внешнего давления приложена в точке
центра тяжести поверхности стенки.
Давление веса жидкости на стенку не
одинаково по высоте: чем глубже расположен
элемент стенки, тем большее давление
веса жидкости он испытывает. Поэтому
центр давления жидкости на вертикальную
стенку расположен всегда ниже центра
тяжести смоченной поверхности стенки.
Если вы помещаете твердый предмет на пол, давление на пол над областью контакта – это вес предмета, разделенного областью на полу. Хороший пример того, как сила на небольшой площади может привести к очень сильному давлению, наблюдается в обуви женщин с высокими шипами. Эти типы обуви могут нанести ущерб некоторым полам из-за очень высокого давления на пол на каблук.
Средний ботинок распределяет вес человека более 20 квадратных дюймов. В некоторых случаях этого достаточно, чтобы повредить пол. Если вы положите жидкость в контейнер, вес этой жидкости будет нажимать на дно контейнера, аналогичную весу твердого объекта. Давление на дно контейнера будет таким же, как если бы вес был из твердого вещества.
Сила полного гидростатического давления
на плоскую стенку равна произведению
гидростатического давления в центре
тяжести этой стенки и ее площади:
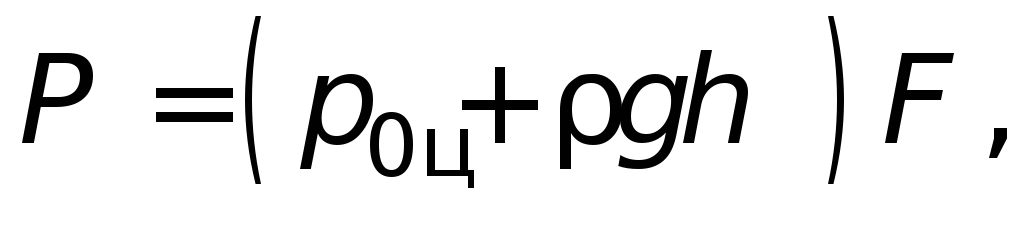 (1.10)
(1.10)
где
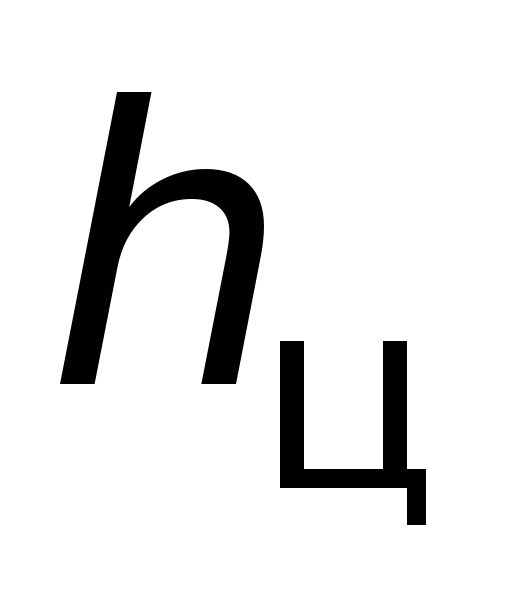 – расстояние от верхнего уровня жидкости
– расстояние от верхнего уровня жидкости
до центра тяжести смоченной поверхности
стенки; оно зависит от геометрической
формы стенки.
Единственное различие заключается в том, что давление в жидкости идет во все стороны. Таким образом, давление на сторонах внизу будет одинаковым. Газы и жидкости проявляют давление из-за их веса в каждой точке жидкости. Давление может быть измерено для твердого тела, нажимая на твердое тело, но в случае твердого тела, нажимающего на жидкость или газ, требуется, чтобы жидкость была ограничена в контейнере. Надавите на себя, чтобы преуспеть.
Самые популярные книги по физике силы. Если да, отправьте электронное письмо с отзывами. Пожалуйста, включите его в качестве ссылки на свой сайт или в качестве ссылки в своем отчете, документе или тезисе. Участники, подверженные воздействию осесимметричных нагрузок.
Точка приложения сил Р
иР
изб носит название центра давленияh
д и может быть определена в соответствии
с законами теоретической механики через
момент инерции смоченной поверхности
стенки
Тонкостенный цилиндр под давлением. Преамбула: сосуды высокого давления чрезвычайно важны в промышленности. Обычно в обычной практике используются два типа сосудов высокого давления, такие как цилиндрический сосуд высокого давления и сферический сосуд высокого давления.
При анализе этих стеновых цилиндров, подвергнутых внутренним давлениям, предполагается, что радиальные планы остаются радиальными, а доза толщины стенки не изменяется из-за внутреннего давления. Далее, при анализе их стеновых цилиндров, вес жидкости считается пренебрежимым.
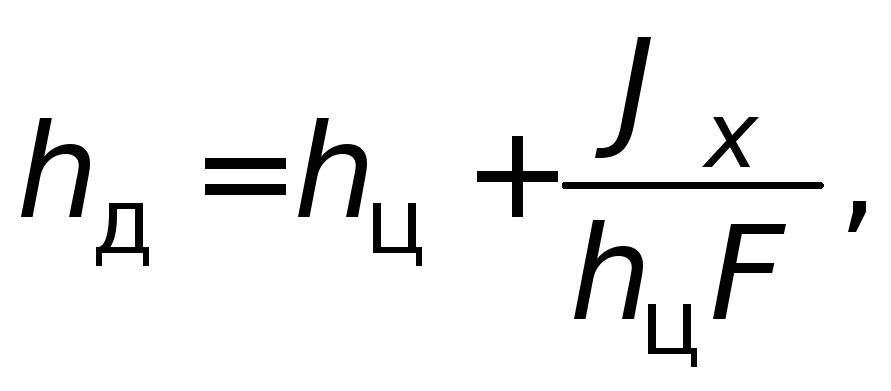 (1.11)
(1.11)
где J
x
– момент инерции
стенки относительно осиox
.
Для прямоугольной стенки при уровне
жидкости в сосуде, равном Н
, и ширине
стенкиВ
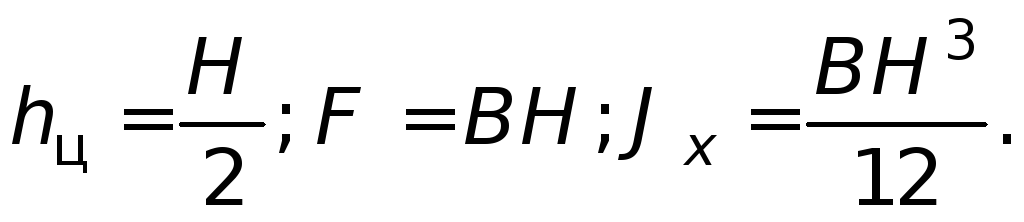
Следовательно,
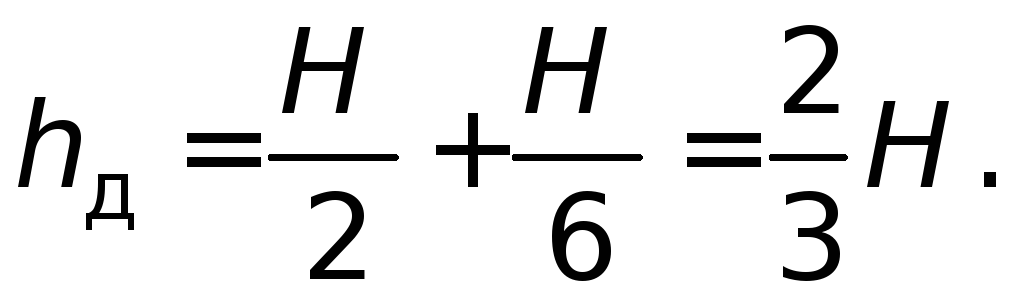
Этот цилиндр подвергается разности гидростатического давления р между его внутренней и внешней поверхностями. Во многих случаях р между давлением избыточного давления внутри цилиндра, заставляя внешнее давление быть окружающим. Небольшой кусок стенки цилиндра показан изолированно, а напряжения в соответствующем направлении также показаны.
Такой компонент не срабатывает, поскольку при чрезмерно высоком внутреннем давлении. Хотя это может потерпеть неудачу, разрываясь по пути, следующему окружности цилиндра. При нормальных обстоятельствах он терпит неудачу по обстоятельствам, которые он терпит неудачу, разрываясь вдоль пути, параллельного оси. Это говорит о том, что напряжение пялец значительно выше, чем осевое напряжение.
Практическое использование законов гидростатики
Применив закон Паскаля к сообщающимся
сосудам, можно прийти к следующим
выводам.
Если сосуды (рис. 1.4 а
) заполнены
однородной жидкостью (одинаковой
плотности), то при равновесии давление
в точке 0 может быть выражено:
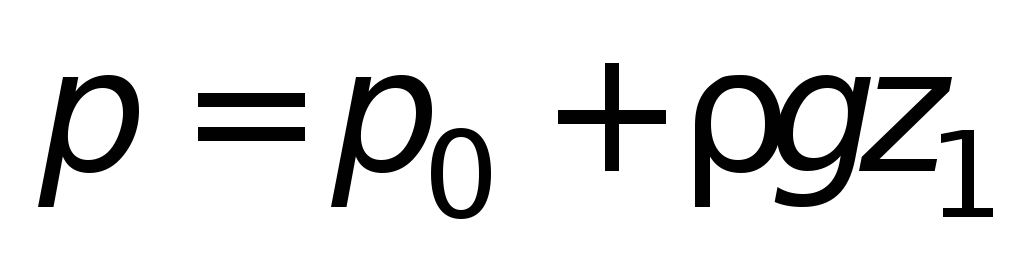 либо
либо
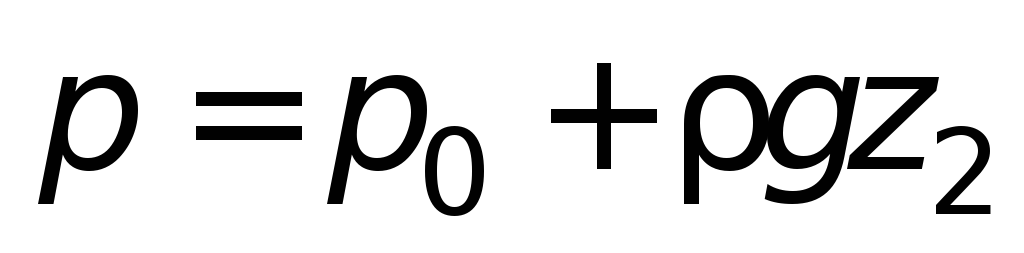 ,
,
Чтобы получить выражения для различных напряжений, сделаем следующее. Жидкие резервуары и емкости для хранения, водопроводные трубы, котлы, корпуса подводных лодок и некоторые компоненты воздушной плоскости являются общими примерами тонкостенных цилиндров и сфер, куполов крыши.
В стенке нет напряжений сдвига. Продольные и пястные напряжения не меняются через стену. Состояние выноса для элемента тонкостенного сосуда высокого давления считается двухосным, хотя внутреннее давление, действующее нормали к стене, вызывает локальное напряжение сжатия, равное внутреннему давлению. На самом деле состояние трехосевого напряжения существует на внутри судна. Однако для тогдашнего стенного сосуда давления третье напряжение намного меньше, чем два других напряжения, и по этой причине в этом можно пренебречь.
т.е. в сообщающихся сосудах заполняющая
их однородная жидкость располагается
на одинаковом уровне.
При заполнении сосудов жидкостями с
различной плотностью (рис 1.4 б
) в
условиях равновесия давление в точке
О будет
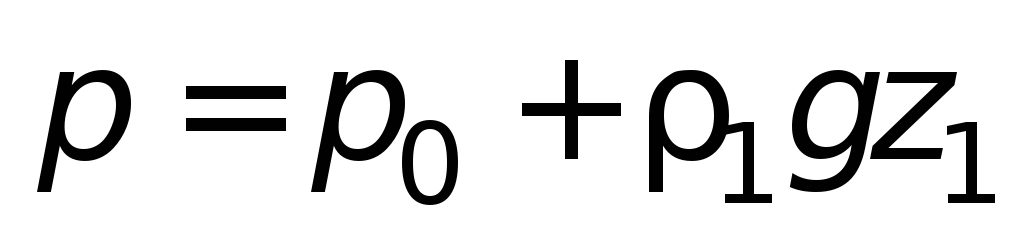 либо
либо
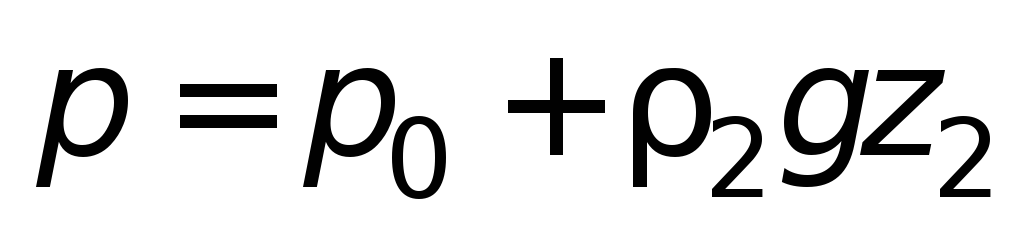 .
.
Тонкие цилиндры, подверженные внутреннему давлению. Когда тонкостенный цилиндр подвергается внутреннему давлению, в материалах цилиндра будут установлены три взаимно перпендикулярных главных напряжения, а именно. Окружность или шероховатость. Теперь определим эти напряжения и определим выражения для них.
Обруч или периферический стресс. Это напряжение, которое создается в противодействии разрушающему эффекту приложенного давления и может быть наиболее удобно обрабатываться с учетом равновесия цилиндра. На рисунке мы показали одну половину цилиндра. Общее усилие на одной половине цилиндра из-за внутреннего давления р.
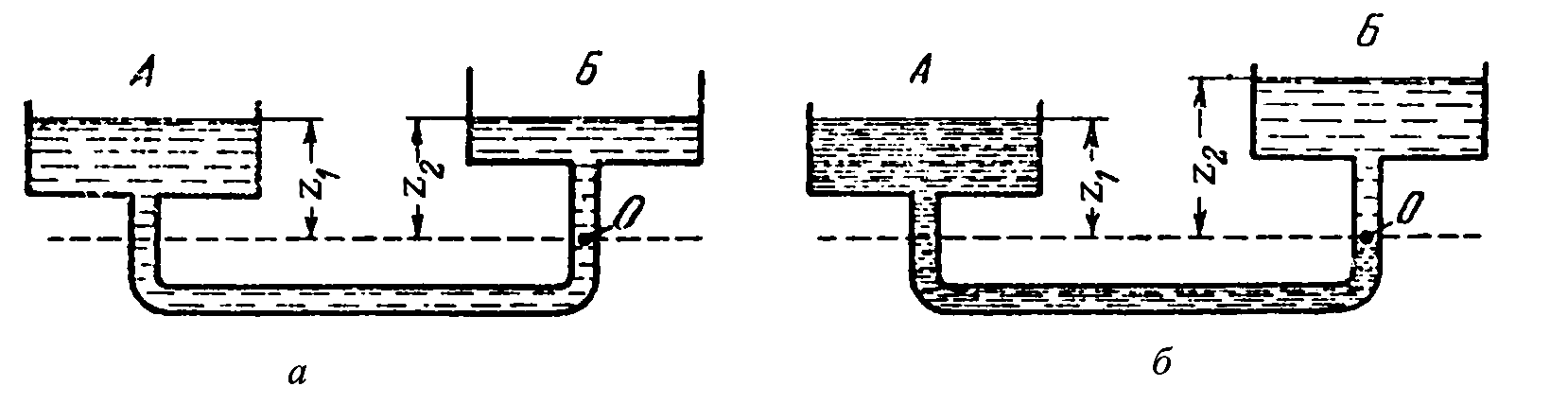
Рисунок 1.4
– Сообщающиеся сосуды, заполненные
жидкостью:
а
– одной плотности;б
– разной плотности
Следовательно
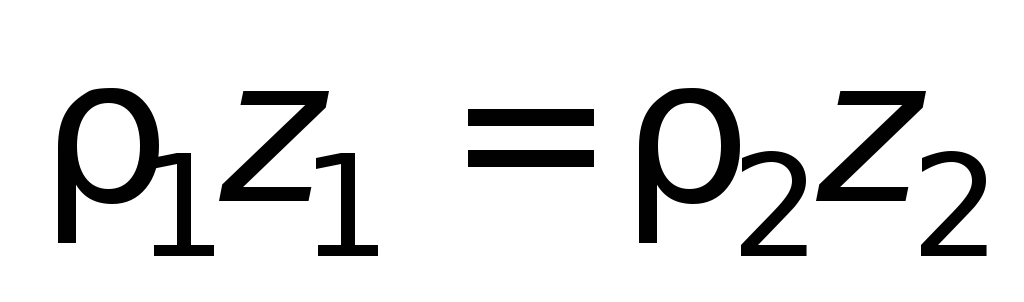 ,
,
т.е.
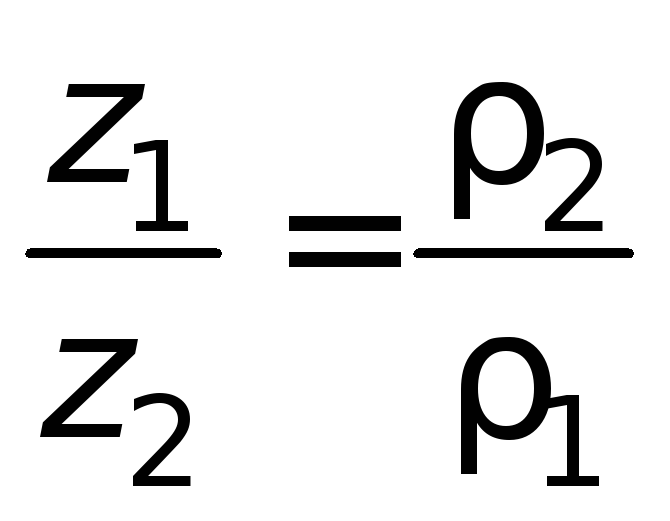 . (1.12)
. (1.12)
Т. – сила в одной стенке полуцилиндра. Требования к сложным системам автоматизированной обработки, потребность во все более жестком управлении технологическими процессами и все более строгая нормативная среда приводят к тому, что инженеры-разработчики стремятся получать более точные и надежные системы измерения уровня. Повышенная точность позволяет снизить изменчивость химического процесса, что приводит к повышению качества продукта, снижению затрат и меньшему количеству отходов. Правила, особенно касающиеся электронных документов, устанавливают жесткие требования к точности, надежности и электронной отчетности.
Соотношение (1.12) указывает на то, что
высоты уровней жидкости, отсчитываемые
от поверхности раздела, обратно
пропорциональны плотностям жидкостей.
Этот принцип используется для измерения
уровня жидкости в закрытых аппаратах
с помощью водомерных стёкол, в жидкостных
манометрах.
Если сообщающиеся сос