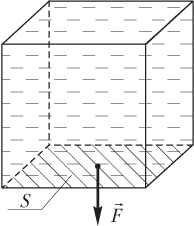
Давление жидкости на вертикальную стенку и дно сосуда
4.2. Элементы гидростатики
4.2.3. Гидростатическое давление
Жидкость, находящаяся в некотором сосуде, оказывает на его дно и стенки гидростатическое давление.
Гидростатическое давление (давление жидкости) на дно сосуда (рис. 4.10) рассчитывают по формуле
pгидр = ρ0gh,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости.
В Международной системе единиц гидростатическое давление измеряется в паскалях (1 Па).
Сила гидростатического давления на дно сосуда (см. рис. 4.10) определяется как произведение:
Fгидр = pгидрS = ρ0ghS,
где pгидр — гидростатическое давление на дно сосуда; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь дна сосуда.
Рис. 4.10
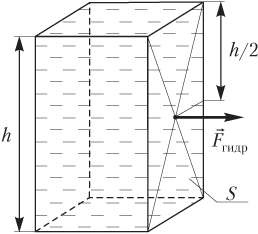
Гидростатическое давление (давление жидкости) на вертикальную стенку сосуда (рис. 4.11) рассчитывают по формуле
pгидр=ρ0gh2,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — высота вертикальной стенки сосуда (столба жидкости).
Рис. 4.11
Сила гидростатического давления на вертикальную стенку сосуда (см. рис. 4.11) определяется как произведение:
Fгидр=pгидрS=ρ0gh2S,
где pгидр — гидростатическое давление на дно сосуда; ρж — плотность жидкости; g — модуль ускорения свободного падения; h — высота столба жидкости; S — площадь вертикальной стенки.
Рис. 4.11
При расчете давленияна днооткрытого водоема (рис. 4.12) необходимо учитывать атмосферное давление:
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h — глубина водоема.
Рис. 4.12
Сила давления на дно открытого водоема определяется произведением:
F = pS = (pатм + ρ0gh)S,
где S — площадь дна водоема.
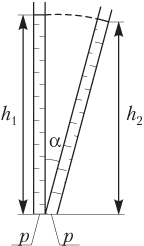
Гидростатическое давление жидкости на дно мензурки (рис. 4.13), отклоненной от вертикали на некоторый угол:
p = ρ0gh1 cos α,
где ρ0 — плотность жидкости; g — модуль ускорения свободного падения; h1 — высота столба жидкости при вертикальном положении мензурки; h2 = h1 cos α — высота столба жидкости при отклонении мензурки на угол α от ее вертикального положения.
Рис. 4.13
Пример 25. Цилиндрический сосуд радиусом 10 см имеет высоту 30 см. Его заполнили до краев жидкостью плотностью 2,5 г/см3. Найти величину средней силы гидростатического давления, действующей на боковую поверхность цилиндра.
Решение. Средняя сила гидростатического давления, действующая на боковую поверхность цилиндра, определяется произведением:
〈Fгидр〉=〈p〉S,
где 〈p〉 — среднее гидростатическое давление на боковую поверхность цилиндра; S — площадь боковой поверхности цилиндра.
Найдем каждый из сомножителей следующим образом:
- среднее гидростатическое давление на боковую поверхность цилиндра
〈p〉=ρ0gh2,
где ρ0 — плотность жидкости, заполняющей сосуд; g — модуль ускорения свободного падения; h — высота цилиндра; т.е. среднее значение гидростатического давления определяется как давление на середину боковой поверхности цилиндра;
- площадь боковой поверхности цилиндра
S = 2πRh,
где 2πr — длина окружности; R — радиус дна цилиндра; т.е. площадь боковой поверхности цилиндра определяется как площадь прямоугольника, одна из сторон которого равна высоте цилиндра, а другая — периметру круга (длине окружности), лежащего в его основании.
Подстановка среднего гидростатического давления 〈p〉 и площади боковой поверхности цилиндра S в исходную формулу позволяет получить выражение для вычисления модуля искомой силы:
〈Fгидр〉=πρ0gRh2.
Расчет дает значение:
〈Fгидр〉=π⋅2,5⋅103⋅10⋅10⋅10−2⋅(30⋅10−2)2≈707 Н≈0,71 кН.
Пример 26. Атмосферное давление составляет 100 кПа. Плотность воды в водоеме равна 1,0 г/см3. Найти глубину открытого водоема, на которой давление в четыре раза больше атмосферного.
Решение. Давление в открытом водоеме определяется формулой
p = pатм + ρ0gh,
где pатм — атмосферное давление; ρ0 — плотность воды; g — модуль ускорения свободного падения; h — искомая глубина водоема.
По условию задачи
p = 4pатм.
Подстановка указанного значения в исходную формулу дает:
4pатм = pатм + ρ0gh,
или
3pатм = ρ0gh.
Выразим отсюда искомую глубину водоема
h=3pатмρ0g
и произведем вычисление:
h=3⋅100⋅1031,0⋅103⋅10=30 м.
Таким образом, давление в открытом водоеме в 4 раза превышает атмосферное на глубине 30 м.
Источник
Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.
Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòàòè÷åñêèì.
Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:
1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:
2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
F=mg. (1.28)
Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:
m = pV, (1.29)
à îáúåì — ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:
V=Sh. (1.30)
Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:
F = pVg=pShg. (1.31)
Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:
pS = pSkg.
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:
p = phg.
Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.
Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàêæå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ — ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.
 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.
Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæàþùèõñÿ — áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñóäîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S — ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ — ñïîñîáíîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.
Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëåíèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâøèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëåíèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июня 2020; проверки требует 1 правка.
Гидростатическое давление — давление столба жидкости над условным уровнем.
Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине w этой поверхности, и направленной по нормали к ней. Отношение P/w, то есть давление р на поверхность, равную единице, называется гидростатическим давлением[1].
Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах[1].
Вычисление[править | править код]
В каждой жидкости существует давление, обусловленное её собственным весом ; так как , то ; учтём, что и получим формулу .
Плотность жидкости зависит от температуры. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением[2].
Для бытовых расчетов можно принять, что с ростом глубины на каждые 10 метров пресной воды, давление увеличивается на 0,1 МПа (1 атмосфера).
История открытия[править | править код]
Это основное свойство жидкостей было открыто и проверено на опыте Блезом Паскалем в 1653 г., хотя несколько ранее оно было уже известно Стевину[источник не указан 1100 дней].
Единица измерения[править | править код]
Единицей измерения давления в международной системе единиц является Паскаль. На практике гидростатическое давление часто измеряют в атмосферах, принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0 °C при нормальном ускорении свободного падения 9,80665 м/с².
На основании гидростатического парадокса можно гидростатическое давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности.
Свойства[править | править код]
Гидростатический парадокс[править | править код]
Гидростатическое давление на тело не зависит от направления.
Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние от каждой такой частицы до свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу гидростатического давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.
Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, гидростатическое давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.
Закон Паскаля[править | править код]
Чем глубже, тем выше давление. (левая часть графика)
Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести ( = несжимаемая жидкость) подчиняется закону Паскаля:
где:
— плотность [для пресной воды: ρ ≈ 1000 кг/м³]
— ускорение свободного падения [для Европы: g ≈ 9,81 м/с²]
— высота (здесь: жидкости) [м]
— [Па]
⇒ = гидростатическое давление (p) зависит от высоты (h) жидкости.[4]
Примечания[править | править код]
Литература[править | править код]
- В. В. Лермантов. Гидростатическое давление // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1893. — Т. VIIIa. — С. 655—656.
Источник
Поскольку на жидкость действует сила тяжести, жидкое вещество обладает весом. Вес — это сила, с которой оно давит на опору, т. е. на дно сосуда, в который налито. Закон Паскаля говорит: давление на жидкость передается в любую ее точку, не меняя своей силы. Как же рассчитать давление жидкости на дно и стенки сосуда? Будем разбираться в статье, используя наглядные примеры.
Опыт
Представим, что у нас есть цилиндрический сосуд, в который налита жидкость. Обозначим высоту слоя жидкости h, площадь дна сосуда — S, а плотность жидкости — ρ. Искомое давление — это P. Его вычисляют путем деления силы, действующей под углом 90° к поверхности, на площадь этой поверхности. В нашем случае поверхность — это дно емкости. P = F/S.
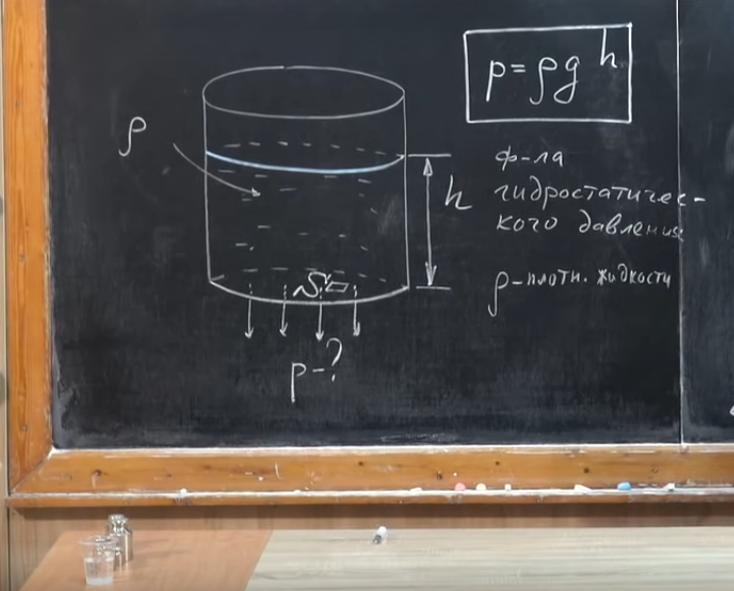
Сила давления жидкости на дно сосуда — это вес. Он равен силе давления. Наша жидкость неподвижна, поэтому вес равен силе тяжести (Fтяж ), действующей на жидкость, а значит, и силе давления (F=Fтяж). Fтяж находят так: умножают массу жидкости (m) на ускорение свободного падения (g). Масса может быть найдена, если известно, какова плотность жидкости и каков ее объем в сосуде. m = ρ×V. Сосуд имеет цилиндрическую форму, поэтому его объем мы будем находить, умножив площадь основания цилиндра на высоту слоя жидкости (V = S×h).
Расчет давления жидкости на дно сосуда
Вот величины, которые мы можем вычислить: V = S×h; m = ρ×V; F = m×g. Подставим их в первую формулу и получим такое выражение: P = ρ×S×h×g/S. Сократим площадь S, стоящую в числителе и знаменателе. Она исчезнет из формулы, а это значит, что давление на дно не зависит от площади сосуда. Кроме того, оно не зависит и от формы емкости.
Давление, которое жидкость создает на дно сосуда, называется гидростатическим. “Гидро” — это “вода”, а статическое — это потому, что жидкость неподвижна. По формуле, полученной после всех преобразований (P = ρ×h×g), определите давление жидкости на дно сосуда. Из выражения видно, что чем более плотная жидкость, тем больше ее давление на дно сосуда. Разберем подробнее, что собой представляет величина h.
Давление в толще жидкости
Допустим, мы нарастили сосуд снизу еще на некоторую величину, добавили дополнительное пространство для жидкости. Если мы поместим в емкость рыбку, давление на нее будет одинаковым в сосуде из предыдущего опыта и во втором, увеличенном? Изменится ли давление от того, что под рыбкой еще есть вода? Нет, потому что сверху находится определенный слой жидкости, на нее действует сила тяжести, значит, вода обладает весом. А то, что снизу, не имеет никакого значения. Следовательно, мы можем найти давление в самой толще жидкости, и h — это будет глубина. Она необязательно является расстоянием до дна, дно может быть и ниже.

Представим, что мы развернули рыбку на 90°, оставив ее на той же глубине. Изменится ли от этого давление на нее? Нет, потому что на глубине оно одинаково во всех направлениях. Если мы приблизим рыбку прямо к стенке сосуда, изменится ли давление на нее, если она будет оставаться на той же глубине? Нет. Во всех случаях давление на глубине h будет вычисляться по той же формуле. Значит, эта формула позволяет найти давление жидкости на дно и стенки сосуда на глубине h, т. е. в толще жидкости. Чем глубже, тем оно больше.
Давление в наклонном сосуде
Представим, что у нас есть трубка длиной около 1 м. Мы налили в нее жидкость так, что она заполнена целиком. Возьмем точно такую же трубку, наполненную до краев, и разместим ее под наклоном. Сосуды одинаковы и заполнены одной и той же жидкостью. Следовательно, масса и вес жидкости и в первой, и во второй трубке равны. Будет ли одинаковым давление в точках, расположенных на дне этих емкостей? На первый взгляд кажется, что давление P1 равно P2, поскольку масса жидкостей одинакова. Предположим, что это так, и проведем эксперимент, чтобы проверить.
Соединим нижние части этих трубок маленькой трубочкой. Если наше предположение о том, что P1 = P2, верное, то перетечет ли куда-то жидкость? Нет, потому что на ее частицы будут действовать силы противоположного направления, которые будут компенсировать друг друга.
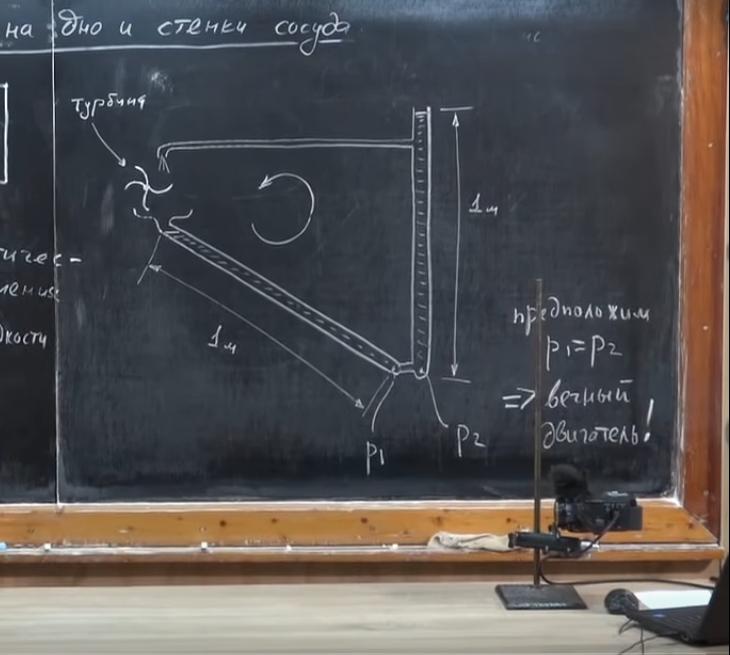
Давайте приделаем к наклонный трубке сверху воронку. А на вертикальной трубке проделаем отверстие, в него вставим трубочку, которая загибается вниз. Давление на уровне отверстия больше, чем на самом верху. Значит, жидкость будет перетекать по тоненькой трубочке и наполнять воронку. Масса жидкости в наклонной трубке будет увеличиваться, жидкость потечет из левой трубки в правую, затем будет подниматься и циркулировать по кругу.
А теперь установим над воронкой турбину, которую соединим с электрическим генератором. Тогда эта система самостоятельно, без какого-либо вмешательства будет вырабатывать электроэнергию. Она будет работать без остановки. Казалось бы, это и есть «вечный двигатель». Однако еще в XIX веке Французская академия наук отказалась принимать любые подобные проекты. Закон сохранения энергии говорит о том, что создать «вечный двигатель» невозможно. Значит, наше предположение о том, что P1 = P2, неверное. На самом деле P1< P2. Как же тогда рассчитать давление жидкости на дно и стенки сосуда в трубке, которая расположена под наклоном?
Высота столба жидкости и давление
Чтобы это выяснить, проведем следующий мысленный эксперимент. Возьмем сосуд, наполненный жидкостью. Поместим в него две трубки из металлической сетки. Одну расположим вертикально, а другую – наклонно, таким образом, что ее нижний конец будет находиться на той же глубине, что и дно первой трубки. Поскольку емкости находятся на одинаковой глубине h, то давление жидкости на дно и стенки сосуда будет тоже одинаковым.

Теперь заделаем все отверстия в трубках. Из-за того, что они стали сплошными, давление в их нижних частях изменится? Нет. Хотя давление и одинаково, а сосуды равны по размеру, масса жидкости в вертикальной трубке меньше. Глубина, на которой находится нижняя часть трубки, называется высотой столба жидкости. Дадим определение данному понятию: это отсчитываемое по вертикали расстояние от свободной поверхности до данной точки жидкости. В нашем примере высота столба жидкости одинакова, поэтому и давление одинаково. В предыдущем опыте высота столба жидкости в правой трубке больше, чем в левой. Поэтому давление P1 меньше, чем P2.
Источник