Давление жидкости в сосуде одинаково во всех точках
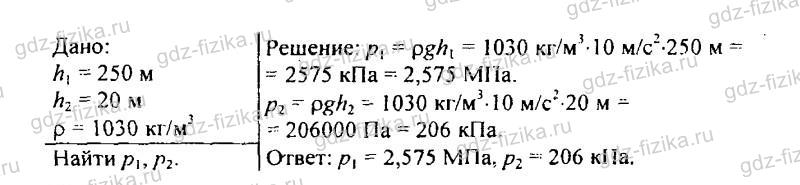
Давление жидкости на дно и стенки сосуда. Формула гидростатического давления
Поскольку на жидкость действует сила тяжести, жидкое вещество обладает весом. Вес — это сила, с которой оно давит на опору, т. е. на дно сосуда, в который налито. Закон Паскаля говорит: давление на жидкость передается в любую ее точку, не меняя своей силы. Как же рассчитать давление жидкости на дно и стенки сосуда? Будем разбираться в статье, используя наглядные примеры.
Представим, что у нас есть цилиндрический сосуд, в который налита жидкость. Обозначим высоту слоя жидкости h, площадь дна сосуда — S, а плотность жидкости — ρ. Искомое давление — это P. Его вычисляют путем деления силы, действующей под углом 90° к поверхности, на площадь этой поверхности. В нашем случае поверхность — это дно емкости. P = F/S.
Сила давления жидкости на дно сосуда — это вес. Он равен силе давления. Наша жидкость неподвижна, поэтому вес равен силе тяжести (Fтяж ), действующей на жидкость, а значит, и силе давления (F=Fтяж). Fтяж находят так: умножают массу жидкости (m) на ускорение свободного падения (g). Масса может быть найдена, если известно, какова плотность жидкости и каков ее объем в сосуде. m = ρ×V. Сосуд имеет цилиндрическую форму, поэтому его объем мы будем находить, умножив площадь основания цилиндра на высоту слоя жидкости (V = S×h).
Расчет давления жидкости на дно сосуда
Вот величины, которые мы можем вычислить: V = S×h; m = ρ×V; F = m×g. Подставим их в первую формулу и получим такое выражение: P = ρ×S×h×g/S. Сократим площадь S, стоящую в числителе и знаменателе. Она исчезнет из формулы, а это значит, что давление на дно не зависит от площади сосуда. Кроме того, оно не зависит и от формы емкости.
Давление, которое жидкость создает на дно сосуда, называется гидростатическим. «Гидро» — это «вода», а статическое — это потому, что жидкость неподвижна. По формуле, полученной после всех преобразований (P = ρ×h×g), определите давление жидкости на дно сосуда. Из выражения видно, что чем более плотная жидкость, тем больше ее давление на дно сосуда. Разберем подробнее, что собой представляет величина h.
Давление в толще жидкости
Допустим, мы нарастили сосуд снизу еще на некоторую величину, добавили дополнительное пространство для жидкости. Если мы поместим в емкость рыбку, давление на нее будет одинаковым в сосуде из предыдущего опыта и во втором, увеличенном? Изменится ли давление от того, что под рыбкой еще есть вода? Нет, потому что сверху находится определенный слой жидкости, на нее действует сила тяжести, значит, вода обладает весом. А то, что снизу, не имеет никакого значения. Следовательно, мы можем найти давление в самой толще жидкости, и h — это будет глубина. Она необязательно является расстоянием до дна, дно может быть и ниже.
Представим, что мы развернули рыбку на 90°, оставив ее на той же глубине. Изменится ли от этого давление на нее? Нет, потому что на глубине оно одинаково во всех направлениях. Если мы приблизим рыбку прямо к стенке сосуда, изменится ли давление на нее, если она будет оставаться на той же глубине? Нет. Во всех случаях давление на глубине h будет вычисляться по той же формуле. Значит, эта формула позволяет найти давление жидкости на дно и стенки сосуда на глубине h, т. е. в толще жидкости. Чем глубже, тем оно больше.
Давление в наклонном сосуде
Представим, что у нас есть трубка длиной около 1 м. Мы налили в нее жидкость так, что она заполнена целиком. Возьмем точно такую же трубку, наполненную до краев, и разместим ее под наклоном. Сосуды одинаковы и заполнены одной и той же жидкостью. Следовательно, масса и вес жидкости и в первой, и во второй трубке равны. Будет ли одинаковым давление в точках, расположенных на дне этих емкостей? На первый взгляд кажется, что давление P1 равно P2, поскольку масса жидкостей одинакова. Предположим, что это так, и проведем эксперимент, чтобы проверить.
Соединим нижние части этих трубок маленькой трубочкой. Если наше предположение о том, что P1 = P2, верное, то перетечет ли куда-то жидкость? Нет, потому что на ее частицы будут действовать силы противоположного направления, которые будут компенсировать друг друга.
Давайте приделаем к наклонный трубке сверху воронку. А на вертикальной трубке проделаем отверстие, в него вставим трубочку, которая загибается вниз. Давление на уровне отверстия больше, чем на самом верху. Значит, жидкость будет перетекать по тоненькой трубочке и наполнять воронку. Масса жидкости в наклонной трубке будет увеличиваться, жидкость потечет из левой трубки в правую, затем будет подниматься и циркулировать по кругу.
А теперь установим над воронкой турбину, которую соединим с электрическим генератором. Тогда эта система самостоятельно, без какого-либо вмешательства будет вырабатывать электроэнергию. Она будет работать без остановки. Казалось бы, это и есть «вечный двигатель». Однако еще в XIX веке Французская академия наук отказалась принимать любые подобные проекты. Закон сохранения энергии говорит о том, что создать «вечный двигатель» невозможно. Значит, наше предположение о том, что P1 = P2, неверное. На самом деле P1 28 марта, 2019
Источник
Относительный покой жидкости. Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
Рис.4.1. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции Pu, равная по величине ma. Равнодействующая этих сил направлена к вертикали под углом α, тангенс которого равен
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α.
Рассмотрим еще один частный случай относительного покоя жидкости. Жидкость находится в сосуде, вращающемся равномерно с угловой скоростью со вокруг своей вертикальной оси (рис.4.2). Когда движение установится, жидкость будет вращаться вместе с сосудом и будет относительно последнего находиться в покое.
Из массовых сил на каждую частицу жидкости, например М (рис. 4.2), в данном случае будут действовать сила тяжести и центробежная сила инерции переносного движения, вызванная вращением жидкости вместе с сосудом.
Для ускорения сил тяжести:
(4.2).2)
Для ускорения центробежных сил инерции переносного движения:
Прежде всего исследуем на основе полученных выражений форму свободной поверхности жидкости в сосуде, рассматривая ее как поверхность
равного давления. Воспользуемся дифференциальным уравнением поверхности равного давления
Подставив значения Fx, Fy, Fz под которыми следует понимать алгебраическую сумму проекций ускорений силы тяжести и силы инерции, получим:
откуда после интегрирования найдем:
Это уравнение показывает, что поверхности
равного давления представляют собой
Рис.4.2 параболоиды вращения. Придавая С
различные значения, получим семейство параболоидов вращения. Для того чтобы получить уравнение свободной поверхности, надо определить Со для нее. Обозначим ординаты свободной поверхности через zСВ.. Учитывая, что в самой низкой точке свободной поверхности при zСВ =z x = 0 и у = 0, получим:
Окончательно, имея в виду, что х 2 + у 2 =г 2 , получим:
Из (4.6) следует, что каждая точка свободной поверхности, например М’, находится над уровнем zQна высоте
Где
— линейная скорость частицы, участвующей во вращательном движении вместе с сосудом и находящейся на расстоянии z от оси вращения.
Теперь найдем закон распределения давления по объему жидкости. В соответствии с выражением для полного дифференциала гидростатического давления в рассматриваемом случае получим:
где r — расстояние частицы от оси вращения. Постоянную С1 определим по давлению рв точке свободной поверхности, расположенной на оси OZ. При этом r = 0; z = zи
Подставляя значение С1в формулу для р, найдем:
Здесь z — координата любой частицы в объеме жидкости.
В связи с тем, что согласно (4.7)
для любой точки, расположенной внутри жидкости, формула (4.12) может быть представлена в виде
где h— глубина погружения частицы, измеряемая от свободной параболической поверхности. Из (4.13) видно, что давление распределяется по гидростатическому закону.
3. Сила давления жидкости на плоские, произвольно ориентированные поверхности.
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.4.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.
Рис. 4.3. Схема к определению равнодействующей гидростатического давления на плоскую поверхность
Избыточное гидростатическое давление в точке А будет равно
Соответственно давление в точке В:
где H — глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно
(4.16)
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна
(4.17)
где hc = Н/2 — глубина погружения центра тяжести плоской поверхности под уровень жидкости.
Однако точка приложения равнодействующей гидростатического давления (ц.д.) не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести, а величина lд равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.
(4.18)
где Jx — момент инерции площади S относительно уреза жидкости.
где J – момент инерции смочено площадки относительно оси, проходящей через центр тяжести площадки параллельно линии уреза жидкости.
(4.19)
В частном случае, когда стенка длиной L имеет форму прямоугольника любой ширины b и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления (ц.д.) находится на расстоянии L/3 от нижней стороны (основания стенки).
Дата добавления: 2014-01-11 ; Просмотров: 929 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Источник
Формула давления жидкости отличается от формулы, с помощью которой можно рассчитать давление твердого тела. Потому, что давление жидкости не зависит от площади поверхности, на которую жидкость давит.
Закон Паскаля
Французский физик, Блез Паскаль, в 1653 году сформулировал закон: «Давление, которое мы оказываем на жидкость (или газ), она без изменения передаст в любую точку и во всех направлениях».
Мы немного упростим формулировку:
Жидкость (или газ) передает давление, оказанное на нее, одинаково и без изменений во все стороны.
Это значит, что на одной и той же глубине жидкость будет одинаково давить и на дно, и на стенки сосуда.
Рис. 1. Чем глубже, тем больше давление жидкости, но в любой точке жидкость передает это давление одинаково во все стороны
На рисунке 1 изображен сосуд, наполненный жидкостью. Высоту столбика жидкости – то есть, глубину, отсчитываем от поверхности жидкости.
Видно, что на разных глубинах давление отличается.
[ large begin{cases} h_{1} < h_{2} < h_{3} \ P_{1} < P_{2} < P_{3} end{cases} ]
Чем глубже, тем больше давление жидкости. Но в любой точке оно одинаково передается во все стороны.
Формула давления жидкости
Формула, по которой можно посчитать давление жидкости:
[ large boxed{ P = rho_{text{ж}} cdot g cdot h }]
( P left(text{Па}right) ) – давление жидкости;
( displaystyle rho_{text{ж}} left(frac{text{кг}}{text{м}^3} right) ) – плотность жидкости;
( displaystyle g left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения;
Для большинства школьных задач можно принимать ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) );
( h left(text{м}right) ) – высота столбика жидкости.
В формулу для давления жидкости не входит площадь S поверхности, на которую эта жидкость давит.
Поэтому, давление жидкости не зависит от площади. А давление твердого тела рассчитывают по другой формуле.
В некоторых задачах указывают объем используемой жидкости. И иногда просят рассчитать силу давления. Чтобы получить правильный ответ для таких задач, нужно уметь переводить площади и объемы в единицы системы СИ.
Сообщающиеся сосуды
Сообщающиеся сосуды – это емкости, расположенные на плоской горизонтальной поверхности, у дна они соединяются трубками.
Если в один из сосудов начать наливать жидкость, то она будет распределяться по всем сосудам, так, что ее уровень будет одинаковым во всех сосудах (рис. 2).
Рис. 2. В сообщающихся сосудах уровень жидкости будет одинаковым
Неважно, какую форму имеет сосуд. Давление жидкости во всех сосудах будет одинаковым. Поэтому одинаковой будет высота h столбика жидкости во всех сосудах.
U-образное колено
U-образное колено – это два сообщающихся сосуда, диаметры сосудов одинаковые.
Жидкости, которые заливают в колено, не должны смешиваться (рис. 3). Например, можно залить в оду трубку воду, а в другую — масло.
Рис. 3. Два сообщающихся сосуда одинакового диаметра образуют U-образное колено
Запишем формулы для расчета давления в левом (P_{1}) и правом (P_{2}) частях колена.
[ large boxed{begin{cases} P_{1} = rho_{1} cdot g cdot h_{1} \ P_{2} = rho_{2} cdot g cdot h_{2} end{cases}} ]
Чем больше разница плотностей двух жидкостей, тем больше отличаются высоты их столбиков.
При решении задач общую нижнюю часть колена не учитываем. На рисунке 3 она отделена от верхней части горизонтальной линией.
Давление столбиков, оставшихся в верхней части, будет одинаковым.
( P_{1} ) – давление жидкости в левой части колена;
( P_{2} ) – давление жидкости в правой части колена.
[ large begin{cases} P_{1} = P_{2} \ rho_{1} cdot g cdot h_{1} = rho_{2} cdot g cdot h_{2} end{cases} ]
Обе части последнего уравнения разделим на ускорение свободно падения. Тогда получим соотношение для высот столбиков жидкости и их плотностей:
[ large boxed{ rho_{1} cdot h_{1} = rho_{2} cdot h_{2} }]
Высоты столбиков можно измерить линейкой. Зная плотность одной из жидкостей, можно найти плотность второй жидкости.
Примечание: Давление жидкостей часто измеряют в миллиметрах ртутного столба или метрах водяного столба. Переходите по ссылке, чтобы узнать, как связаны эти единицы измерения и как давление переводить в систему СИ.
Гидравлический пресс
Молекулы жидкости плотно упакованы, они прилегают друг к другу. Поэтому жидкости не сжимаемы! Это свойство жидкостей используют в гидравлическом прессе.
Гидравлический пресс – это два сообщающихся сосуда. Их называют цилиндрами. Диаметры цилиндров отличаются. Внутри каждого цилиндра вверх и вниз может свободно перемещаться поршень (рис. 4). Поршень плотно прилегает к стенкам цилиндра, чтобы жидкость из цилиндра не просачивалась наружу.
Рис. 4. Гидравлический пресс – это два сообщающихся сосуда различных диаметров, по сосудам могут без трения перемещаться поршни
Перемещаясь, поршень из цилиндра вытесняет жидкость в соседний цилиндр. Объем жидкости, вытесненной из одного цилиндра, совпадает с объемом, перешедшим в другой цилиндр, так как жидкость не проливается наружу.
[ large Delta V_{1} = Delta V_{2} ]
( Delta V_{1} left(text{м}^{3}right) ) – объем жидкости, вытесненной из первого цилиндра;
( Delta V_{2} left(text{м}^{3}right) ) – объем жидкости, перешедшей во второй цилиндр.
Из геометрии известно, объем цилиндрической фигуры можно найти по формуле:
[ large boxed{ Delta V = Delta h cdot S }]
( Delta h left(text{м}right) ) – высота столбика вытесненной жидкости;
( S left(text{м}^{2}right) ) – площадь поршня (или основания цилиндра);
Так как объемы вытесненной и перешедшей в другой цилиндр жидкостей равны, можем записать
[ large Delta h_{1} cdot S_{1} = Delta h_{2} cdot S_{2} ]
То есть, высоты столбиков отличаются во столько же раз, во сколько отличаются площади поршней.
Площадь поверхности поршня и его диаметр связаны соотношением:
[ large boxed{ S_{text{круга}} = pi cdot frac{d^{2}}{4} }]
( S left(text{м}^{2}right) ) – площадь поршня;
( d left(text{м}right) ) – диаметр поршня;
Давления в цилиндрах будут равны.
[ large P_{text{общ.лев}} = P_{text{общ.прав}} ]
Поршни в цилиндрах не двигаются – т. е. находятся в равновесии. Запишем условия равновесия для поршней:
[ large boxed{ frac{F_{1}}{S_{1}} + rho_{1} cdot g cdot h_{1} = frac{F_{2}}{S_{2}} + rho_{2} cdot g cdot h_{2} } ]
Здесь дробью вида (displaystylelarge frac{F}{S}) обозначено давление твердого тела (ссылка) — поршня.
Назовем цилиндр большого диаметра большим цилиндром, а цилиндр малого диаметра – малым. Сформулируем принцип действия гидравлического пресса:
С помощью малой силы в малом цилиндре мы можем создавать большую силу в большом цилиндре.
Источник
504. Сосуд с жидкостью наклонили (рис. 131). Одинаковое ли давление оказывает после этого жид¬кость на боковые стенки А и В в точках, лежащих на одном горизонтальном уровне?
Жидкость оказывает одинаковое давление на одном горизонтальном уровне везде, в том числе и на стенках А и В (см. рис. 131).
505. Сосуд с водой имеет форму, изображенную на рисунке 132. Одинаково ли давление воды на боковые стенки сосуда на уровне аб?
На уровне ab давление воды на боковые стенки одно и то же (см. рис. 132).
506. Цилиндрические сосуды уравновешены на весах (рис. 133). Нарушится ли равновесие весов, если в них налить воды столько, что поверхность ее установится на одинаковом уровне от дна сосудов? Одинаково ли будет давление на дно сосудов?
Равновесие весов нарушается, так как в разных сосудах различная масса воды. Давление на дно сосуда будет одинаковым, так как высота столба воды в обоих сосудах одна и та же (см. рис. 133)
507. Цилиндрические сосуды уравновешены на весах (см. рис. 133). Мальчик налил в оба сосуда воду одинаковой массы. Нарушилось ли равновесие весов? Одинаково ли будет давление воды на дно сосудов?
Равновесие весов не нарушилось. Давление воды на дно сосуда будет различным, так как уровень налитой воды будет различным (см. рис. 133).
508. В цилиндрический сосуд, частично заполненный водой, опустили деревянный брусок. Изменилось ли давление воды на дно сосуда?
Давление воды на дно увеличилось, так как при опускании в воду деревянного бруска ее уровень поднялся.
509. В трех сосудах с одинаковой площадью дна налита вода до одного уровня (рис. 134). В каком сосуде налито больше воды? Одинаково ли давление на дно в этих сосудах? Почему?
Воды налито больше в крайнем левом сосуде. Давление на дно будет одинаковым во всех трех сосудах, так как везде вода налита до одного уровня (см. рис. 134).
510. Уровень воды в сосудах одинаковый (рис. 135). Будет ли переливаться вода из одного сосуда в другой, если открыть кран?
При открывании крана вода из одного сосуда в другой переливаться не будет, так как уровень воды в сосудах будет одинаковый, а следовательно давление воды на любом уровне так же одинаково (см. рис. 135).
511. Уровень жидкостей в сосудах (см. рис. 135) одинаковый. В левом налита вода, в правом — керосин. Одинаковы ли давления на дно? Одинаковы ли давления на кран? Будет ли переливаться жидкость из одного сосуда в другой, если открыть кран?
Давление воды на дно и на кран больше, чем давление керосина. Объясняется это тем, что плотность воды больше плотности керосина. Если кран открыть, то вследствие разности давлений вода потечет в сосуд с керосином (см. рис. 135).
512. В левой части сосуда над жидкостью находится воздух (рис. 136). Какую высоту столба жидкости следует учитывать при расчете давления на дно сосуда: высоту Н или высоту H1? Ответ объясните.

513. В полиэтиленовый мешок налита вода (рис. 137). Что показывают динамометры: давление или силы, действующие на столики динамометров? Стрелка правого динамометра закрыта листом бумаги. Каково показание правого динамометра? Будут ли изменяться показания динамометров, если воду в мешок доливать (выливать)? Ответы обоснуйте.
Динамометры показывают силы давления жидкости на боковые стенки сосуда с водой. Показания их одинаковы и равны 70Н. Если воду в мешок доливать, то показания динамометров увеличатся, а если воду выливать, то уменьшатся, т.к. увеличится либо уменьшится давление столба жидкости (см. рис.137).
514. Одинаково ли давление воды на дно сосудов (рис. 138)? Чему равно это давление? Изменится ли давление, если воду заменить керосином? Чему оно будет равно в этом случае?

515. Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, налитая до того же уровня?
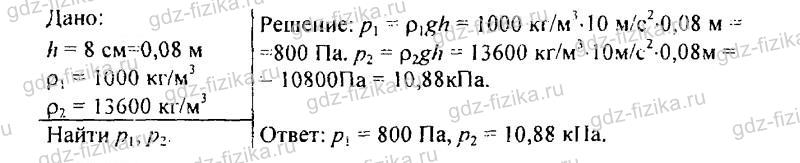
516. Какое давление на дно сосуда оказывает слой керосина высотой 0,5 м?

517. В цилиндрический сосуд налиты ртуть, вода и керосин. Определите общее давление, которое оказывают жидкости на дно сосуда, если объемы всех жидкостей равны, а верхний уровень керосина находится на высоте 12 см от дна сосуда.
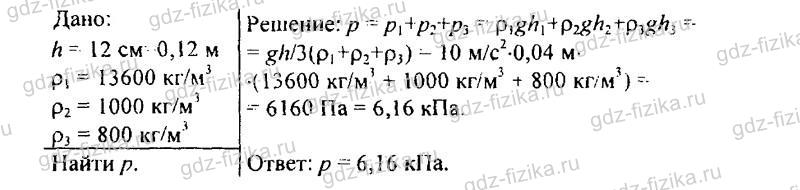
518. Сосуды с водой имеют равные площади дна (рис. 139). В каком из них избыточное давление воды на дно (без учета атмосферного давления) больше и во сколько раз?

519. Водолаз в жестком скафандре может погружаться в море на глубину 250 м, искусный ныряльщик — на глубину 20 м. На сколько и во сколько раз отличаются давления воды на этих глубинах?
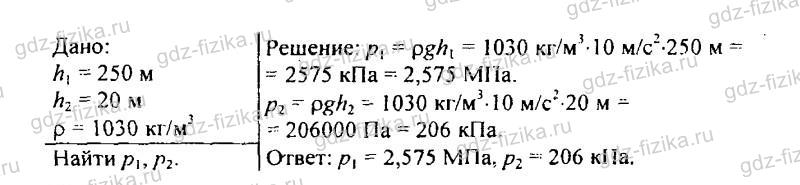
520. Рассчитайте давление воды: а) на самой большой глубине Тихого океана — 11 035 м; б) на наибольшей глубине Азовского моря — 14 м (плотность воды в нем принять равной 1020 кг/м3).
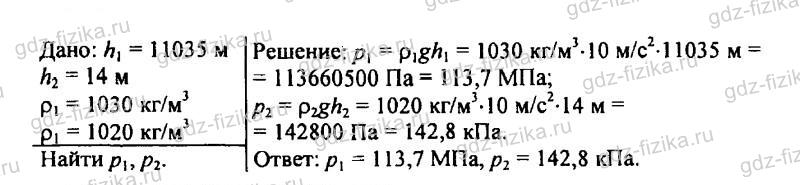
521. Определите по графику (рис. 140) глубину погружения тела в озеро, соответствующую давлению воды 100, 300 и 500 кПа.
10 м; 30 м; 50 м (рис. 140).
522. Аквариум наполнен доверху водой. С какой силой давит вода на стенку аквариума длиной 50 см и высотой 30 см?
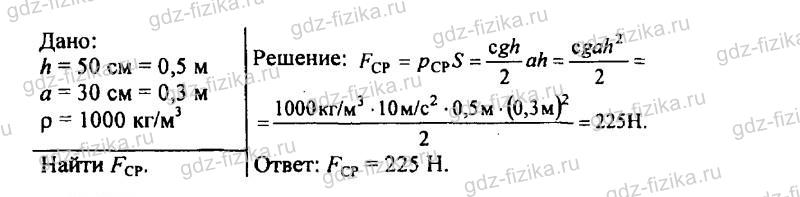
523. В аквариум высотой 32 см, длиной 50 см и шириной 20 см налита вода, уровень которой ниже края на 2 см. Рассчитайте: а) давление воды на дно; б) вес воды; в) силу, с которой вода действует на стенку шириной 20 см.
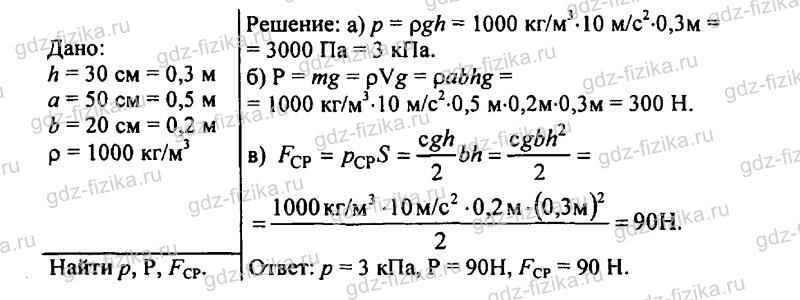
524. Ширина шлюза 10 м. Шлюз заполнен водой на глубину 5 м. С какой силой давит вода на ворота шлюза?
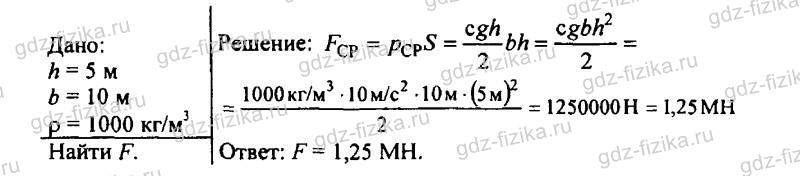
525. В цистерне, заполненной нефтью, на глубине 3 м имеется кран, площадь отверстия которого 30 см2. С какой силой давит нефть на кран?

526. Прямоугольный сосуд вместимостью 2 л наполовину наполнен водой, а наполовину керосином, а) Каково давление жидкостей на дно сосуда? б) Чему равен вес жидкостей в сосуде? Дно сосуда имеет форму квадрата сo стороной 10 см.

527. Определите силу, с которой действует керосин на квадратную пробку площадью поперечного сечения 16 см2, если расстояние от пробей до уровня керосина в сосуде равно 400 мм (рис. 141).

528. Какую силу испытывает каждый квадратный метр площади поверхности водолазного костюма при погружении в морскую воду на глубину 10 м?
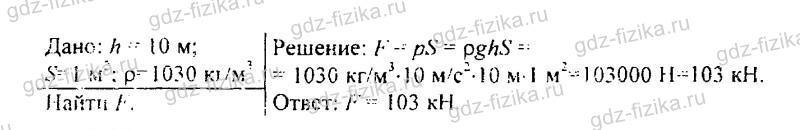
529. Плоскодонная баржа получила пробоину в дне площадью 200 см2. С какой силой нужно давить на пластырь, которым закрывают отверстие, чтобы сдержать напор воды на глубине 1,8 м? (Вес пластыря не учитывать.)
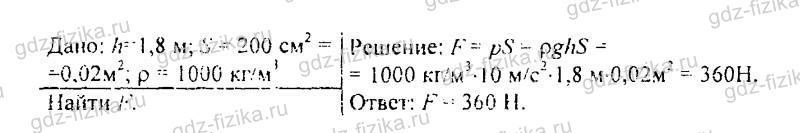
530. Определите высоту уровня воды в водонапорной башне, если манометр, установленный у ее основания, показывает давление 220000 Па.
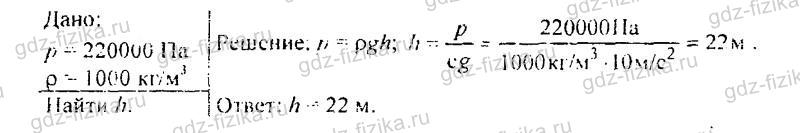
531. На какой глубине давление воды в море равно 412 кПа?
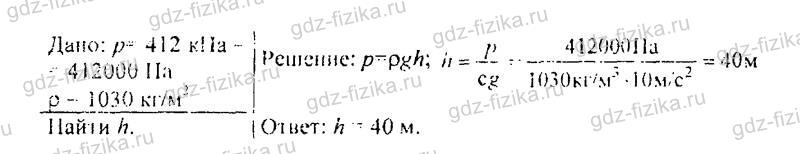
532. Напор воды в водокачке создается насосом. Определите на какую высоту поднимается вода, если давление, созданное насосом, равно 400 кПа?
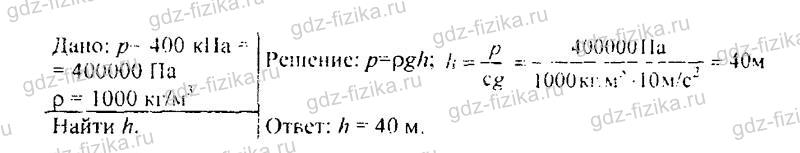
533. Брусок размером 0,5×0,4×0,1 м находится в баке с водой на глубине 0,6 м (рис. 142). Вычислите: а) с какой силой вода давит на верхнюю грань бруска; б) на нижнюю грань бруска; в) сколько весит вода, вытесненная бруском.
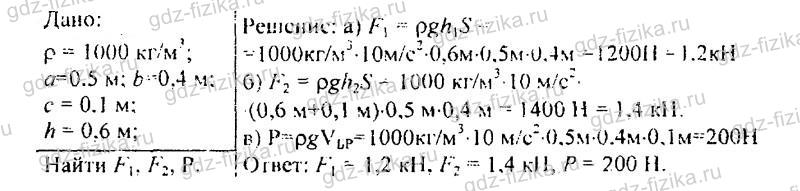
534. Произведите расчет, взяв данные предыдущей задачи, предполагая, что воду заменили керосином.
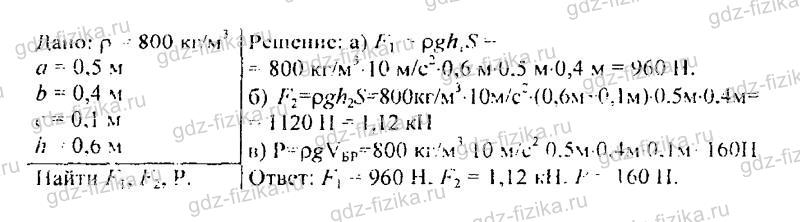
535. Используя результаты двух предыдущих задач, вычислите, на сколько сила, действующая на тело снизу, больше силы, действующей на тело сверху: а) в воде; б) в керосине. Сравните полученные результаты с весом вытесненной воды и с весом вытесненного керосина.

536. Один из кофейников, изображенных на рисунке 143, вмещает больше жидкости, чем другой. Укажите какой и объясните.
Правый кофейник вмещает больше жидкости, чем левый, гак как у него кончик носика находится выше.
537. Точкой А обозначен уровень воды в левом колене трубки (рис. 144). Сделайте рисунок и на нем отметьте точкой В уровень воды в правом колене трубки.

538. В сообщающиеся сосуды налита вода. Что произойдет и почему, если в левый сосуд долить немного воды (рис. 145); в средний сосуд долить воды (рис. 146)?
Уровень воды увеличится во всех сосудах на одинаковую высоту. Таким образом, уровни снова выравнятся (рис. 145, 146).
539. Справедлив ли закон сообщающихся сосудов в условиях невесомости? Объясните почему.
Закон сообщающихся сосудов в условиях невесомости не действует, так как жидкости в состоянии невесомости не обладают весом и потому не оказывают давления на дно сосудов.
540. Как при помощи сообщающихся сосудов проверить, горизонтально ли нанесена филенка (линия, отделяющая окраску панели от верхней части стены)?
Нужно взять длинную тонкую резиновую трубку, вставить стеклянные трубки на концах, залить эту систему водой, а концы стеклянных трубок подвести к филенке. Используя свойство сообщающихся сосудов, пройтись с одной из стеклянных трубок вдоль стены.
541. Объясните действие фонтана (рис. 147).
Действие фонтана объясняется тем, что давление жидкости в верхнем конце правой трубки будет больше атмосферного, так как уровень воды в этой трубке меньше уровня воды в левой трубке.
542. В левом колене сообщающихся сосудов налита вода, в правом — керосин (рис. 148). Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
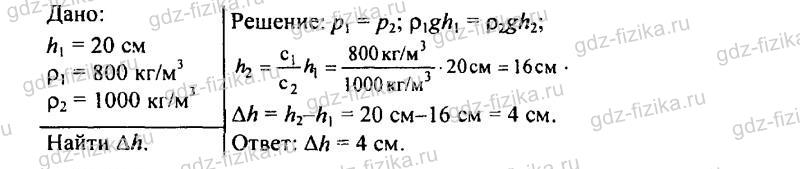
543. В сообщающихся сосудах находятся ртуть и вода (рис. 149). Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?

544. В сообщающихся сосудах находилась ртуть. Когда в правую трубку налили слой керосина высотой 34 см, то уровень ртути в левой трубке поднялся на 2 см. Какой высоты следует налить слой воды в левую трубку, чтобы ртуть в трубках установилась на одинаковом уровне (рис. 149)?
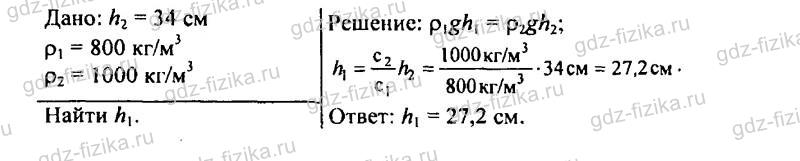
545. В сообщающихся сосудах находятся ртуть, вода и керосин (рис. 150). Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?

Источник
