Давление жидкости в сосуде расчет
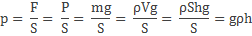
Что такое давление жидкости
Наука гидростатика исследует ситуации, когда движение в жидкости отсутствует или скорость пренебрежимо мала, и позволяет понять некоторые свойства такой важной гидродинамической величины, как давление.
Теорема
Давление – физическая величина, описывающая силу, которая действует перпендикулярно поверхности на единицу ее площади. Для ее обозначения используется символ р или Р.
На опору под действием силы тяжести давят и твердые, и сыпучие вещества, но их воздействие отличается от гидростатического давления. Воздействие твердого тела определяется его весом, жидкости – ее глубиной. В газе и жидкости давящее воздействие на поверхности создается за счет хаотических столкновений молекул и связано с другими параметрами состояния вещества – например, температурой Т и плотностью (rho.)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для жидкости, учитывая ее малую сжимаемость, вместо уравнения Клапейрона, учитывающего температуру и молярную массу газа, обычно используют условие несжимаемости, которое существенно упрощает уравнения гидроаэромеханики:
(rho = const.)
Сила гидростатического давления р на дно сосуда не зависит от его формы и изменяется пропорционально уровню налитой в сосуд жидкости и ее плотности в соответствии с основной гидростатической формулой:
(р = р_{0} + rhos gs h.)
(rho) здесь – плотность вещества, (р_{0}) – атмосферное давление, g – ускорение свободного падения, h – глубина погружения.
История открытия
Гидростатика как наука была достаточно хорошо известна еще в античные времена, поскольку она тесно связана с практической деятельностью людей. Для строительства лодок и кораблей, колодцев и различных гидравлических аппаратов, например, поршневых насосов, необходимо было понимать, как вода взаимодействует с твердыми материальными предметами.
Различие между давлением твердого тела и воды очень эффектно пояснил на опыте Блез Паскаль: всего лишь стакан воды, вылитый в высокую тонкую трубку, соединенную с наполненной водой закрытой бочкой, создал такое избыточное давление, что вода через щели брызнула наружу.
Определение
В 1653 году Паскаль сформулировал свой закон: давление, производимое на жидкость или газ, передается в любую точку одинаково.
Позже был сконструирован прибор, демонстрирующий действие закона Паскаля. Он называется шар Паскаля и представляет собой заполняемый водой шар с маленькими отверстиями, соединенный с цилиндрической рукояткой, внутри которой движется поршень. Внешнее давление, производимое поршнем, передается во все точки воды одинаково, и она выплескивается в виде одинаковых струек. Поэтому струйки, вытекающие из отверстий, расположенных в горизонтальной плоскости, оставляют на полу следы равной длины.
Факторы, влияющие на показатель
На давление жидкости могут влиять:
- ее плотность;
- атмосферное давление;
- температура;
- глубина сосуда;
- площадь дна сосуда.
Давление на дно и стенку сосуда
Закон Паскаля утверждает, что давление в любом месте покоящейся жидкости или газа по всем направлениям одинаково, причем оно одинаково передается по всему объему вещества. Таким образом, разницы между давлением на дно и на стенку нет.
Расчет давления жидкости на дно и стенки сосуда
Чтобы найти давление на дно сосуда, нужно взять приведенное выше основное уравнение гидростатики и подставить туда глубину, плотность и атмосферное давление.
В случае стенок непосредственно прилагать эту формулу можно только к бесконечно малым горизонтальным полоскам на боковых стенках сосуда. Чтобы рассчитать давление на стенки, нужно суммировать давление на все горизонтальные элементы их поверхности, используя правила интегрального исчисления. Паскаль, проведя эти расчеты, доказал, что от формы сосуда давление жидкости не зависит.
Единицы измерения
В международной системе единиц давление измеряется в Паскалях. Один Паскаль равен силе в один ньютон, производящей равномерное давление на единицу поверхности в один метр. Но на практике часто используют такую единицу измерения, как атмосфера, равную 76 см ртутного столба при нулевой температуре по Цельсию.
Определение
Атмосфера – внесистемная единица измерения, которая примерно означает давление атмосферы Земли на уровне Мирового океана.
Формулы расчета
Для описания процессов в гидравлических прессах или любых других системах, в которых давление собственно жидкостей ничтожно мало по сравнению с передаваемым им извне, используется формула закона Паскаля:
(р = frac{F}{S}.)
F – сила, с которой происходит воздействие на поверхности сосуда, S – площадь этой поверхности.
В учебных задачах обычно опускают такой параметр, как атмосферное давление, и используют для расчетов формулу:
(р = rhos gs h.)
Можно вывести эту формулу для сосудов, имеющих форму прямой призмы или цилиндра, из закона Паскаля.
(m = rhos V = rhos Ss h)
Вес (Р = g s m = gs rhos Ss h.)
Вес столба, давящего на дно сосуда, равен силе, и тогда:
(р = frac{Р}{S} = gs rhos Ss frac{h}{S} = gs rhos h.)
Применение на практике
Для гидравлических механизмов, например, прессов, можно рассчитать пропорциональный изменению площади выигрыш в силе, зная, во сколько раз увеличивается площадь большего поршня по сравнению с меньшим.
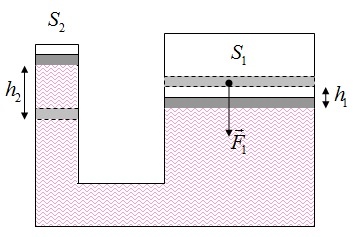
Соотношение между полезной и затраченной работой описывается понятием КПД, коэффициент полезного действия, и рассчитывается по формуле:
(frac{F_{2}h_{2}}{F_{1}h_{1}})
Также закон Паскаля описывает работу жидкостных манометров, приборов для измерения давления, отличного от атмосферного. Давление в одном колене манометра вызывает повышение жидкости в другом колене – это явление называется избыточным столбом. По его высоте, соотнося ее с нанесенной шкалой, пользователь прибора узнает точную цифру в миллиметрах ртутного столба.
Гидростатический парадокс
Согласно гидростатическому парадоксу, давление жидкости на любую плоскую стенку равняется весу столба этой жидкости, давящему на основание, площадь которого равна площади этой стенки. Поэтому от формы емкости давление не зависит. Если емкость расширяется к горлышку, то вес содержимого распределяется по наклонным стенкам и передается вниз через стенки, не давя на дно, а если емкость к горлышку сужается, то содержимое давит на стенки снизу вверх, что уменьшает его воздействие на дно.
Источник
Содержание:
- § 1 Особенности давления в жидкости и газе
- § 2 Формула для вычисления давления в жидкостях и газах
- § 3 Решение задачи по теме урока
- § 4 Краткие итоги по теме урока
§ 1 Особенности давления в жидкости и газе
Известно, что давление, производимое на жидкости и газы, передается в каждую точку без изменения по всем направлениям. Это утверждение называется законом Паскаля.
На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому верхние слои жидкости давят на нижележащие слои, это давление по закону Паскаля передается по всем направлениям. Значит, внутри жидкости существует давление. Чтобы убедиться в этом, поставим опыт.
Возьмем стеклянную трубочку, затянутую снизу резиновой пленкой. Если в трубочку нальем воду, то увидим, что резиновая пленка прогибается. На резиновую пленку действуют две силы: вес воды, направленный вниз, из-за чего пленка изменяет свою форму, и возникающая при деформации сила упругости, которая стремится восстановить первоначальную форму и направленная вверх. Если две эти силы равны, то пленка будет находиться в покое.
Опустим трубку с водой в другой, более широкий, сосуд с водой. Возникает третья сила, действующая на резиновую пленку, – сила давления воды снизу, она направлена вверх и заставляет пленку выпрямляться. Если уровни воды в трубке и в сосуде совпадут, то силы давления, действующие сверху и снизу на пленку, окажутся равными.
Такой же опыт проведем с трубкой, в которой есть боковое отверстие, затянутое резиновой пленкой. Если в трубку налить воду, то пленка выгибается наружу, так как вода давит не только на дно трубки, но и на стенки. Опустим трубку в воду и заметим, что пленка выпрямляется, то есть силы, действующие на пленку изнутри и снаружи, оказались равными.
Итак, опыты показывают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям.
Такое же утверждение справедливо и для газов.
§ 2 Формула для вычисления давления в жидкостях и газах
От чего зависит давление в жидкостях и газах?
Вспомним определение давления.
Давление – скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: p = F/S.
Сила давления Fравна весу P: P = mg.
Мы знаем, что массу тела можно найти по плотности вещества: m = ρV, где ρ – плотность, V – объем.
Объем жидкости, находящейся в сосуде в форме прямоугольного параллелепипеда или в форме цилиндра, можно найти, умножив площадь дна на высоту сосуда: V = Sh. Подставим формулы веса, массы, объема в формулу давления и, сократив площадь, получим:
Мы вывели формулу для вычисления давления в жидкостях и газах:
p = gρh.
Из этой формулы видно, что давление жидкости на дно сосуда зависит только от плотности и высоты столба жидкости.
По формуле p = gρhможно рассчитывать:
1)давление жидкости на дно в сосуде любой формы, то есть давление жидкости не зависит от формы сосуда;
2)давление жидкости на стенки сосуда, так как давление на одной и той же глубине одинаково по всем направлениям: вверх, вниз, вправо, влево, вперед, назад;
3)давление в газах.
Проверим единицу измерения давления по формуле p = gρh.
g – коэффициент тяжести, измеряется в Н/кг,
ρ – плотность, в международной системе единиц измеряется в кг/м3,
h – высота столба жидкости (глубина) – в м.
§ 3 Решение задачи по теме урока
Рассмотрим решение задачи:
Задача:Определить давление воды на дно морской впадины, глубина которой 10900 м. Плотность морской воды – 1030 кг/м3.
Решение: Запишем условие задачи: нам известны глубина h = 10900 м, плотность ρ = 1030 кг/м3. Необходимо найти: давление p. Для решения: запишем формулу расчета давления в жидкостях и газах p = gρh и подставим числовые значения:
p = 10 Н/кг · 1030 кг/м3· 10 900 м = 112 270 000 Па = 112, 27 МПа.

Ответ: 112, 27 МПа
§ 4 Краткие итоги по теме урока
ВАЖНО ЗАПОМНИТЬ:
На жидкости и газы действует сила тяжести, поэтому они обладают весом. Вышележащие слои жидкости и газа своим весом давят на нижележащие слои, то есть оказывают давление. Давление внутри жидкости и газа на одном и том же уровнеодинаково по всем направлениям.
Давление в жидкостях и газах рассчитывается по формуле p = gρh, где g – коэффициент тяжести, ρ – плотность, h – высота столба жидкости или газа.
Давление в жидкостях и газах зависит только от плотности и высоты столба жидкости или газа и не зависит от формы и площади поперечного сечения сосуда, в котором находится жидкость или газ.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
- Я иду на урок физики: 7 класс. Часть III: Книга для учителя. – М.: Издательство «Первое сентября”, 2002. – 272 с.
Источник
Æèäêîñòè (è ãàçû) ïåðåäàþò ïî âñåì íàïðàâëåíèÿì íå òîëüêî âíåøíåå äàâëåíèå, íî è òî äàâëåíèå, êîòîðîå ñóùåñòâóåò âíóòðè íèõ áëàãîäàðÿ âåñó ñîáñòâåííûõ ÷àñòåé.
Äàâëåíèå, îêàçûâàåìîå ïîêîÿùåéñÿ æèäêîñòüþ, íàçûâàåòñÿ ãèäðîñòàòè÷åñêèì.
Ïîëó÷èì ôîðìóëó äëÿ ðàñ÷åòà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè íà ïðîèçâîëüíîé ãëóáèíå h (â îêðåñòíîñòè òî÷êè A íà ðèñóíêå).

Ñèëà äàâëåíèÿ, äåéñòâóþùàÿ ñî ñòîðîíû âûøåëåæàùåãî óçêîãî ñòîëáà æèäêîñòè, ìîæåò áûòü âûðàæåíà äâóìÿ ñïîñîáàìè:
1) êàê ïðîèçâåäåíèå äàâëåíèÿ p â îñíîâàíèè ýòîãî ñòîëáà íà ïëîùàäü åãî ñå÷åíèÿ S:
2) êàê âåñ òîãî æå ñòîëáà æèäêîñòè, ò. å. ïðîèçâåäåíèå ìàññû m æèäêîñòè íà óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ:
F=mg. (1.28)
Ìàññà æèäêîñòè ìîæåò áûòü âûðàæåíà ÷åðåç åå ïëîòíîñòü p è îáúåì V:
m = pV, (1.29)
à îáúåì – ÷åðåç âûñîòó ñòîëáà è ïëîùàäü åãî ïîïåðå÷íîãî ñå÷åíèÿ:
V=Sh. (1.30)
Ïîäñòàâëÿÿ â ôîðìóëó (1.28) çíà÷åíèå ìàññû èç (1.29) è îáúåìà èç (1.30), ïîëó÷èì:
F = pVg=pShg. (1.31)
Ïðèðàâíèâàÿ âûðàæåíèÿ (1.27) è (1.31) äëÿ ñèëû äàâëåíèÿ, ïîëó÷èì:
pS = pSkg.
Ðàçäåëèâ îáå ÷àñòè ïîñëåäíåãî ðàâåíñòâà íà ïëîùàäü S, íàéäåì äàâëåíèå æèäêîñòè íà ãëóáèíå h:
p = phg.
Ýòî è åñòü ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ.
Ãèäðîñòàòè÷åñêîå äàâëåíèå íà ëþáîé ãëóáèíå âíóòðè æèäêîñòè íå çàâèñèò îò ôîðìû ñîñóäà, â êîòîðîì íàõîäèòñÿ æèäêîñòü, è ðàâíî ïðîèçâåäåíèþ ïëîòíîñòè æèäêîñòè, óñêîðåíèÿ ñâîáîäíîãî ïàäåíèÿ è ãëóáèíû, íà êîòîðîé îïðåäåëÿåòñÿ äàâëåíèå.
Âàæíî åùå ðàç ïîä÷åðêíóòü, ÷òî ïî ôîðìóëå ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ìîæíî ðàññ÷èòûâàòü äàâëåíèå æèäêîñòè, íàëèòîé â ñîñóä ëþáîé ôîðìû, â òîì ÷èñëå, äàâëåíèå íà ñòåíêè ñîñóäà, à òàêæå äàâëåíèå â ëþáîé òî÷êå æèäêîñòè, íàïðàâëåííîå ñíèçó ââåðõ, ïîñêîëüêó äàâëåíèå íà îäíîé è òîé æå ãëóáèíå îäèíàêîâî ïî âñåì íàïðàâëåíèÿì.
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ .
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ – ÿâëåíèå, çàêëþ÷àþùååñÿ â òîì, ÷òî âåñ æèäêîñòè, íàëèòîé â ñîñóä, ìîæåò îòëè÷àòüñÿ îò ñèëû äàâëåíèÿ æèäêîñòè íà äíî ñîñóäà.
 äàííîì ñëó÷àå ïîä ñëîâîì «ïàðàäîêñ» ïîíèìàþò íåîæèäàííîå ÿâëåíèå, íå ñîîòâåòñòâóþùåå îáû÷íûì ïðåäñòàâëåíèÿì.
Òàê, â ðàñøèðÿþùèõñÿ êâåðõó ñîñóäàõ ñèëà äàâëåíèÿ íà äíî ìåíüøå âåñà æèäêîñòè, à â ñóæàþùèõñÿ – áîëüøå.  öèëèíäðè÷åñêîì ñîñóäå îáå ñèëû îäèíàêîâû. Åñëè îäíà è òà æå æèäêîñòü íàëèòà äî îäíîé è òîé æå âûñîòû â ñîñóäû ðàçíîé ôîðìû, íî ñ îäèíàêîâîé ïëîùàäüþ äíà, òî, íåñìîòðÿ íà ðàçíûé âåñ íàëèòîé æèäêîñòè, ñèëà äàâëåíèÿ íà äíî îäèíàêîâà äëÿ âñåõ ñîñóäîâ è ðàâíà âåñó æèäêîñòè â öèëèíäðè÷åñêîì ñîñóäå.

Ýòî ñëåäóåò èç òîãî, ÷òî äàâëåíèå ïîêîÿùåéñÿ æèäêîñòè çàâèñèò òîëüêî îò ãëóáèíû ïîä ñâîáîäíîé ïîâåðõíîñòüþ è îò ïëîòíîñòè æèäêîñòè: p = pgh (ôîðìóëà ãèäðîñòàòè÷åñêîãî äàâëåíèÿ æèäêîñòè). À òàê êàê ïëîùàäü äíà ó âñåõ ñîñóäîâ îäèíàêîâà, òî è ñèëà, ñ êîòîðîé æèäêîñòü äàâèò íà äíî ýòèõ ñîñóäîâ, îäíà è òà æå. Îíà ðàâíà âåñó âåðòèêàëüíîãî ñòîëáà ABCD æèäêîñòè: P = oghS, çäåñü S – ïëîùàäü äíà (õîòÿ ìàññà, à ñëåäîâàòåëüíî, è âåñ â ýòèõ ñîñóäàõ ðàçëè÷íû).
Ãèäðîñòàòè÷åñêèé ïàðàäîêñ îáúÿñíÿåòñÿ çàêîíîì Ïàñêàëÿ – ñïîñîáíîñòüþ æèäêîñòè ïåðåäàâàòü äàâëåíèå îäèíàêîâî âî âñåõ íàïðàâëåíèÿõ.
Èç ôîðìóëû ãèäðîñòàòè÷åñêîãî äàâëåíèÿ ñëåäóåò, ÷òî îäíî è òî æå êîëè÷åñòâî âîäû, íàõîäÿñü â ðàçíûõ ñîñóäàõ, ìîæåò îêàçûâàòü ðàçíîå äàâëåíèå íà äíî. Ïîñêîëüêó ýòî äàâëåíèå çàâèñèò îò âûñîòû ñòîëáà æèäêîñòè, òî â óçêèõ ñîñóäàõ îíî áóäåò áîëüøå, ÷åì â øèðîêèõ. Áëàãîäàðÿ ýòîìó äàæå íåáîëüøèì êîëè÷åñòâîì âîäû ìîæíî ñîçäàâàòü î÷åíü áîëüøîå äàâëåíèå.  1648 ã. ýòî î÷åíü óáåäèòåëüíî ïðîäåìîíñòðèðîâàë Á. Ïàñêàëü. Îí âñòàâèë â çàêðûòóþ áî÷êó, íàïîëíåííóþ âîäîé, óçêóþ òðóáêó è, ïîäíÿâøèñü íà áàëêîí âòîðîãî ýòàæà, âûëèë â ýòó òðóáêó êðóæêó âîäû. Èç-çà ìàëîé òîëùèíû òðóáêè âîäà â íåé ïîäíÿëàñü äî áîëüøîé âûñîòû, è äàâëåíèå â áî÷êå óâåëè÷èëîñü íàñòîëüêî, ÷òî êðåïëåíèÿ áî÷êè íå âûäåðæàëè, è îíà òðåñíóëà.

Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июня 2020; проверки требуют 7 правок.
Гидростатическое давление – давление столба жидкости над условным уровнем.
Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р, пропорциональной величине w этой поверхности, и направленной по нормали к ней. Отношение P/w, то есть давление р на поверхность, равную единице, называется гидростатическим давлением[1].
Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах[1].
Вычисление[править | править код]
В каждой жидкости существует давление, обусловленное её собственным весом ; так как , то ; учтём, что и получим формулу .
Плотность жидкости зависит от температуры. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением[2].
Для бытовых расчетов можно принять, что с ростом глубины на каждые 10 метров пресной воды, давление увеличивается на 0,1 МПа (1 атмосфера).
История открытия[править | править код]
Это основное свойство жидкостей было открыто и проверено на опыте Блезом Паскалем в 1653 г., хотя несколько ранее оно было уже известно Стевину[источник не указан 1297 дней].
Единица измерения[править | править код]
Единицей измерения давления в международной системе единиц является Паскаль. На практике гидростатическое давление часто измеряют в атмосферах, принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0 °C при нормальном ускорении свободного падения 9,80665 м/с².
На основании гидростатического парадокса можно гидростатическое давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности.
Свойства[править | править код]
Гидростатический парадокс[править | править код]
Гидростатическое давление на тело не зависит от направления.
Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние от каждой такой частицы до свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу гидростатического давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления, давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.
Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, гидростатическое давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.
Закон Паскаля[править | править код]
Чем глубже, тем выше давление. (левая часть графика)
Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести ( = несжимаемая жидкость) подчиняется закону Паскаля:
где:
– плотность [для пресной воды: ρ ≈ 1000 кг/м³] – ускорение свободного падения [для Европы: g ≈ 9,81 м/с²] – высота (здесь: жидкости) [м] – [Па]
⇒ = гидростатическое давление (p) зависит от высоты (h) жидкости.[4]
Примечания[править | править код]
Литература[править | править код]
- В. В. Лермантов. Гидростатическое давление // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). – СПб., 1893. – Т. VIIIa. – С. 655-656.
Источник
