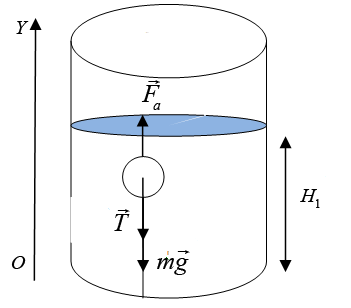
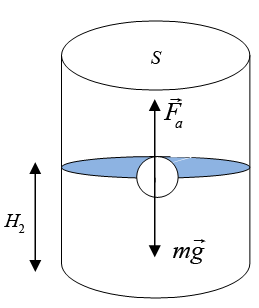
Деревянный шар объема v привязан нитью к дну сосуда

Статьи

Среднее общее образование

Физика

Предлагаем вашему вниманию разбор 29 задания ЕГЭ-2018 по физике. Мы подготовили пояснения и подробный алгоритм решения, а также рекомендации по использованию справочников и пособий, которые могут понадобиться при подготовке к ЕГЭ.

20 марта 2018

Задание 29

Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой T. Если нить перерезать, то шар всплывёт, а уровень воды изменится на h = 5 см. Найдите силу натяжения нити T.

Решение


Рис. 1	Рис. 2

Первоначально деревянный шар привязан нитью ко дну цилиндрического сосуда площадью дна S = 100 см2 = 0,01 м2 и полностью погружен в воду. На шар действуют три силы: сила тяжести со стороны Земли, – сила Архимеда со стороны жидкости, – сила натяжения нити, результат взаимодействия шара и нити. По условию равновесия шара в первом случае геометрическая сумма всех действующих на шарик сил, должна быть равна нулю:

ЕГЭ-2018. Физика. Сдаем без проблем!

В книге содержатся материалы для успешной сдачи ЕГЭ по физике: краткие теоретические сведения по всем темам, задания разных типов и уровней сложности, решение задач повышенного уровня сложности, ответы и критерии оценивания. Учащимся не придется искать дополнительную информацию в интернете и покупать другие пособия. В данной книге они найдут все необходимое для самостоятельной и эффективной подготовки к экзамену. Издание содержит задания разных типов по всем темам, проверяемым на ЕГЭ по физике, а также решение задач повышенного уровня сложности.

Купить

Выберем координатную ось OY и направим ее вверх. Тогда с учетом проекции уравнение (1) запишем:

Fa1 = T + mg (2).

Распишем силу Архимеда:

Fa1 = ρ · V1g (3),

где V1 – объем части шара погруженной в воду, в первом это объем всего шара, m – масса шара , ρ – плотность воды. Условие равновесия во втором случае

Fa2 = mg (4)

Распишем силу Архимеда в этом случае:

Fa2 = ρ · V2g (5),

где V2 – объем части шара, погруженной в жидкость во втором случае.

Поработаем с уравнениями (2) и (4) . Можно использовать метод подстановки или вычесть из (2) – (4), тогда Fa1 – Fa2 = T, используя формулы (3) и (5) получим ρ · V1g – ρ · V2g = T;

ρg (V1 – V2) = T (6)

Учитывая, что

V1 – V2 = S ·h (7),

где h = H1 – H2; получим

T = ρ · g · S · h (8)

Подставим числовые значения

T = 1000	кг	· 10	м	· 5 · 10–2 м = 5 Н
	м3		с2

Ответ: 5 Н.

ЕГЭ-2018. Физика. 30 тренировочных вариантов экзаменационных работ

Издание содержит:
• 30 тренировочных вариантов ЕГЭ
• инструкцию по выполнению и критерии оценивания
• ответы ко всем заданиям
Тренировочные варианты помогут учителю организовать подготовку к ЕГЭ, а учащимся – самостоятельно проверить свои знания и готовность к сдаче выпускного экзамена.

Читайте также: Болит сосуд возле глаза

Купить

Источник

Í¥N|%×Ù mïé×õÇÝ =N_fAB$IdÇ£F
÷±ÃüÓz«3Í¥N{ôP]m¨¬,*$+Hr6ôP,49ÉB¡ó¡·HñÙ-÷77ÜÚàÚEÎ)’áu¹ugB_ñ÷¡S,¾òP«£:d89§PÁUíøPAÒàV/k÷SÀð©¤×*qöoJDtH,ãRÙÌÆ²RjÏÃç¬úÅÙîo÷uaeîÎPLèµÐOC°ÎUw¬~émÒ?9ëy¾ÜtPaJ7MpZ3 ¼zIËµÑR{Lz¬ìTíÜ4vjà°%k²Õ ¬eVòVy#dë
)ä-ÞÊòlä
º°êÅÕ4ycÁÌ é|¤ÇIýi(h
²xÓùÓÔÛ^3ÛS=`¦×oVÎÏ9Ü+¶KD ú :@T1.>lhòè§Dz¼Ø«Úó9_èL·º³ïÖ ‘À×ÉãËNÈ#4Ês¼À9&¡üdÊ1
ßJ¹§ióKÚvwaë§H}5x¼&>E×Òuêº¤OO®H¨îXmJºUÈOsi¶ê_¸Ä oZc8Þ¾ÐP°æ¹/TBtUFP¼×¬u¯Í£¬øx%&S£(æ¬,·¯¸øú¼L·E©”fJÙJfnbr§%gü!9ÏKI^|B953ÉÐHÏ¸ºÉ0Þ¤ÔÜÅ95MÓÓh?Õjce.,Ó}ÊPI.¢:úÏ¢äb¶¨Vµ¸|fyA±;ìvÅjHJI)))ÉÊ8kY
Ë¥»¢Y;VRÈ.âÚä(m¶øxãâ%¡ßè§7õÎ®qÿ¸°ÍfÊn+ä
äbg@)ùC!g÷ÅªYêHfo
=f+²ÜÈmØé´~³¦%9!j¯ÏÑ^Tyã$ ãµ1©©& ø20K”2ÇøKî¢úñts}OÝi%4C5:3s2«úéüó½JXx>©³?Ù+¸ w/®ÇíÞlÕ«’En=å´)Å9bþ@¢6@G¼1â@Ü¼D9¡4@2m]L|ê%ÅE ¢gQóÆ9LÖC)«sos¤`ÕùG?¾ ²æitßé)ý$ì [³SÕÕÓÁIýTµÇPiHÅU1V+1a
‘¥¢ÑÑæ%¢¨dÙÑýî9½¬W¡D]¬gàªt1ÙIé.m¡«qA{LïµyKrhFb¹j!Å~?«Ý]ºw>woð{7fe/¸¥wéà%ëî&ËLï{åÜkçÞÐÆÏõ.-]O¨~{-äFÍvgº-.¹ÀÊ;¨Ùe2Ç[tIÌRÛ
¢íuLº-5^ççñ,~À0h
´ãYÚ:ò”^Gè@â3Ä I4²hÊñ¼üsÖæ>4ÖY´Tð´9ë¤mûqSSzÇ£ZÙ
I¥þ§h¬
$Y.³WYi¢ã’+j§òJ$J
r%Ü{*
3]ÞÅ°y~s=tÁÒÞ] Ñe%Í??»ªÐQÑX¹»÷î~½ªÃSyÿ®½ÏßHÚÓ¡³M¦EHJZvÛæ³==èAÎiàÇ¼ÎL¯9y¶2ÌÙËâ$sq²ÏMo3áÆIwòcN&&=’@âÇ÷FBujçs
N1hªROÚ¯;Ó¡M²ÛlYöD»-ÖiVm$3 .ÛF¬zL,F³
ðü%.Þ£Ä;wÂü¶¯1eF=ÕfJ3ßÃÏHI¿µ$XÕÝY¤ZÍRÌ|KRøTY)F?-ù¿,Eí®]/½7¼lðwÍqÏ,ÚÕºõñ5-ßTl)ß|n×Y·îüåÍ»ÜvðèþÒdÙW_xdûë}eÇ/zÑÜàoxmÃ@nÔß®§8p*HÖbÈnÛáiòÄAÑ>iòÄ=ñóâ0ä&9ç¬¹’H/0GÄíMö&v?ÀX2¦F-ÆZìºXm,6Êlh¼X«
²E+3ZÌÖ”+pã+S ,Ôìeå¸Å±@CÓ°¨KY^uãÆGC½~óÓùYB-Fò¸ê×Ä7ì®o8àÛËÝ¡só?½Û³rþtÌNOLvVÝ²§ôpÍººûØ+ì$OûÕx:§ÂærM²*¯.ÁéhX`þÑ”¦§¥#wÔÊîCêF/T3Vi.IÕkÙ¯Í&I

9Mât$
xIeWÄKpùIR$RØü¤RéhÑ¾í;&&vl¸z×å»w/_±/ß>1±q[$¿ÍÀ;s.NýËÃAoSp”wH(GDxÒ ÝáÕ |@ÀH>^Ä§ åD 1oætÖb ö&h$sVËs$Üw+½ZFS¬UÝÜÏâöÙ¤¦,`”×Á³Á³Sl7¸UïâÙ9¬ÁsøV~ëA¤n¦°aEy!eìo ÉV·àÂqîOß^GWâK{;ÕÓæUú¾u`=ðÆãMÄ’¦ÇÆý9º ìZÇmç2ûÑ7Ní?pêÔý§hMRo#áÙ²c®VÒôRkê:÷åkIØäI]i_ÍSþ)ùTç]jNwÀm”ÍvÛtîØX[zqÉVvÄ¡
Ø-$èa7ÉàÙAÜ’§1ðæ$²fãb|«ÂNíÄ$à~Vôíþ¢í¡ÏætÇå’~«»h~Ù·½93ãÿ¡[óÝû]û®[öàÁ4ckµ³4tê»Ýû®[ÉçFîß·è´§Ík)ââÐ³¡suãýF¼¹Ù4ñ2¾U_SWCcEd=.OJ÷q0jx
Ëâ¥Ð¸ødÆ¬ëR¯ÖÀ.ûRY6.99E§¡¤¬ImOÂo¹?ãÖ`åmÞtÝo5ß2jfHMMÇpûÕZÍtÓ3ÅXû3ÆÚ$Ùj½{ØáÄ[)^±ýOÕÓh
¯xæØHíHM
.øbB¸;Ó7±üÂÂUÞÃdYï¡6VY9>w´µ«¿÷®Ðë³*C¼£WýÍñÂCø>$ÿê+¸vÐ´þ)¼ÎëG¸À¿ùßWEa8
çþ ÊWÀþÿÔ5ÐÂ¶K¿;ÝÑ[0áyä÷Fyùo£øÌà±(O å)ÄDyËOEyùé(/B&5¶¬ïéõu÷ÈÈm}=2û7!,k7®Üèê’¯èÎë|C¾Q©u&·lf%äùë°]Qeea&ÅùrÍÀ¼¸UßÐ&yqÏ¦Ã=+ÌÛ²p¡«udm×à@SÛ?ÏBÀzè^ðA7RAl>oAX8%C-æ6″ÏR÷«5d,ÀöùÈÕ©å¾ÿ°§KÉÐØ|©Î&,42^T”B^+VKk°Å ÒÅØfê0¤¶ZýmBÜÃ®0æB,D`ÿ0k¡K ÇgµWá¸¨ßÆQ÷?F¼ó$%¨ÞHAógÿÝ2%$DþÌJwÅ1w]ç3Y£·áYYøßïÃ¡Ùñ2ÆþÓ&êùÿ#À ÉÎ
endstream
endobj
13 0 obj
>
stream
x ÕÀÐØÀÀàÀ0Hzt00041 K7Ñ
endstream
endobj
11 0 obj
>
endobj
10 0 obj
>
/BaseFont /JBFPLL+SymbolMT
>>
endobj
8 0 obj
>
endobj
16 0 obj
>
stream
hÞÜ{y`TEÖï©ª{»Ó I: aN: K-@g Q¢Yd¸!Ä]#QQÜæIÓq qqÑ!(è0~:3*ô}¿ª{ohïýñh~÷Ô^§ªN:µÅR ª3>Ï×nÊÄ{òP3uîÚÅ Ï%z,-ºh¡§öÛ¿_÷ùDQY3j/;Ó3å'”×4″ýÛË¯¸n80¥¨:¨mÝÌéS¦ðõ_Lôô¿P^¿HÒÚÝD_
ÆÌ¹¯ýgË?iúÖ^1ê÷Áj¢+ð/;åÚÚvh×”ÿ.¤÷Ì2wzýÁE D7i]jç/X¾ñïñ2¾öªéµsæ
DTr(©Í_&¢ôUzopiR±fðD¦s%ºÎ¶zÍtm!JqÉòª*=q*c½il³aÈý´>JÖFþJ[¢³¸RÏýÀP¹ÌKÞÐlc¯HBÝ&¬t+eÐZN¯Ò%ô6TÊzQ5i¬u$ÎÐHæ¦ö¤³hêN^ILåô%¥õt}ÍÊè&Ich5¥ÓhjGô[ZÃé&úÍ¢uÈýóS7Å-4*PÑ zV±8JEL4ó{PÂº6ÑGdÐDZ¡¯A)4æ/Ñ$zMdiÍ£%´¥-´ÝÉ5Ý¨¡¾t]Å,u7ÏP¾Ëõñ¦ñ¹þQzgkeÆ7ä§3fbÄ¨7~óè1z>cX_QLqÔu]Bi½èÓ]hÛ&v[/â’Ðþ4Ò^v-kæiú.ýq=%¢}}Ài==A¯Ñt¥±*174ÔM¢(JQÓt;={¿7Y

tòß}ìb-707¡Ý¯ðâm~?[ôzp0&ó&±ÿ~qøBüß]¢¢C½C/Ó;úZ²~¶ñNô
ôáýb
¯äX?1H»M{Zç:ðù8oáN¾)a4&Ó¬#}«]HGÑÿ;ôzôißÃÖñ¼¼ài%¡é¬?¸F/Ðô[¶QxØ»¥ô¦½’¹ÕòNñ¡|c Fh#klã=Cõ³ÛèSñ#dÿB6åÑS´£¾õa©ZHK¡÷¡ùºÒCÚ¿Q#æàµÌ ïi£èCµ½ó¼oJôâö^ál¯4÷©¡W@WI=Gë! Ð”jF¢í,½ø¡c7¢{iH¦Lñ$¯ãøæ¡ßÑ^1
µÞýÔõAIsiÚá1¾
=fS°ËØD*AÌpêjÌçOAùIÆJ}Mï²Q,^öê^®»BGòyÌÃOi8»CÓ¨ëJÉ|¦#ú”½A_«?¯¿¢owG×bÖ>Qü¾ÃªáaSÑ_Ó?!ëE=9?àb8Ö°+ø±Y’ªì½]>Rn¦eOOb
y17D¯Ð.ÌöçSQÊI`ÔÐSÐ·°FL£®Ôýô#c|!êzv9ôl3xú¾æ0_9l+ÁèM¥Ê¹úQ%Û5ùE²D¼C_RV×”ÌÑ’¯²G]h¾qÊ 6
ø,±µÃj©ªÂÊ>] .âÑÌÆPßÐ0¶º¬R«o6Vd¬]¤_ ¾wc%{®2ªÙ*’f¿è*ÿÐ!Ï4p@Aÿ¾}zûÎËÏëÝ³G÷nYÞô4Oj×.S:uìÐ¾]rÛ¤Äw|lhWÓ¡k3Ê)õÕxY5-Ë;|x®ô{§ `JX@MÀ ²SÓÒo¦ô·¦dnÏùt~n§Ôë l/ñzØÄ±ÕpßSâà Qî
ånPîX¸ÓÒÁSÚaf’ÀjÚgöÞÚ
¬ý¦¼}éÀ
¢bÁT ·¤4ÐÑ[“9ÌÒ)Óc«KKRÒÒ&äæXñTïeòâ³U*VÕÅ§ªÆ3K¶îölÈi®_Öä¦Ëj²ÛLóN2©: ¦Lu$d£Þ@ûë÷w8éEáÅÕwÇ¦úÒ³ÙÙ*³}Ó½¥2¤f¶’àòygÖÏ®ÁÐtªÐ¸ëÒ:ù7{©S©§¾ªÚâ0¥¤ó¶T?îºÆ~OÇScrs6¸ÌÝo9ÚÄ;¦·Æ)J.]#Çµö,yG@ ©pRíE
ägzÕO-@2üÀ+0
#2+à*®©wá2@Ït{=õß$À{äð©!S¬G¦û{N)’¢xÛÈÎôì)EÄY1C¿onÎ¢&þ·ÖíA÷Q%úvÊyèþ´49Àw7ùé2xuc«M¿.K ?/{B×Èf;&ùSgÇ´f¯ñB’¹CJDeµþw·K*90ÀÚýLôt3~äxïÈ±«=¥õ5Vß¬:ÅgÆ´ÆY®@RqµHá§¡ÔXzªÛ´Lüw(¡ÖäTªæ)¸kß Ñii¿0SqLæRäd6ÍÀÀìSýNñÂ^zµ,>²jb}}ô)qeÐ@õõe^OY}Mý&£î2¯Çíß{¦[}mi=¢MÆ¦»SeË& 3Ù@H+§¢
^vçØ
~vçøÕÝØÝYUä×MØ¸ê(]Ê[C¥Ï#}ØYAÒ

Источник

Комбинированные задачи по механике

Особенность задания № 29 заключается в том, что в нем требуется использование материалов не менее чем из двух-трех разделов механики. Актуальные сведения, необходимые для решения задания, приведены в разделе теории. Законы сохранения, силы, действующие в макромире, и другая нужная информация содержится в разделах теории соответствующих типовых заданий по механике.

Теория к заданию №29 ЕГЭ по физике

Проекции сил, скорости, ускорения

При решении расчетных задач векторные величины требуется представлять в их скалярных (числовых) значениях. Для этого их выражают в виде проекций на оси выбранной инерционной с-мы координат, например: Fx, vY. Система координат может быть представлена единственной осью (Ox или Oy), если речь идет о движении по горизонтальной плоскости, о свободном падении тела и т.п. При перемещении тела под углом к горизонту и в других более или менее сложных случаях требуется прямоугольная система (Oxy).

Если направление вектора физ.величины совпадает с направлением координатной оси (или одной из осей, когда задача решается в рамках прямоугольной с-мы координат), то величина проекции совпадает с величиной ее модуля. К примеру, если тело бросают вертикально вниз с ускорением

, то представив схему движения в системе Ox, ось которой направлена тоже вертикально вниз, получим для расчетов: .

Если векторная величина направлена по отношению к осям под углом, то вектор вместе со своими проекциями на оси прямоугольной системы координат образует прямоугольный треугольник, в котором вектор – гипотенуза, а проекции – катеты. Приняв угол между вектором и осью Оx равным α (на рисунке представлен пример для вектора ускорения),

величины проекций определяют таким образом:

;

Закон Архимеда

На помещенное в жидкость тело действует выталкивающая его сила. Эта сила традиционно обозначается как FA и вычисляется по формуле:

где ρ – плотность жидкости, в которую помещено тело,

– ускорение свободного падения, V – объем погруженного тела. Относительно объема нужно отметить важный момент: если тело погружено полностью, то для расчета должен браться полный его объем; если тело погружено частично, то следует использовать объем части тела, находящейся в толще жидкости.

Разбор типовых вариантов №29 по физике

Демонстрационный вариант 2018

Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S=100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой Т. Если нить перерезать, то шар всплывет, а уровень воды изменится на h=5 см. Найдите силу натяжения нити Т.

Алгоритм решения:

Переводим числовые данные, приведенные в условии, в СИ. Записываем необходимое для решения табличное значение для плотности жидкости (воды).
Анализируем начальную ситуацию (шар на нити). Определяем силы, действующие на шар.
Анализируем ситуацию после перерезания нити. Определяем силы, действующие на шар. Составляем уравнение для вычисления объема вытесненной части шара.
Применяя 3-й з-н Ньютона, составляем уравнения силы для начальной ситуации (1) и последующей (2). Из этой системы выражаем Т. Используя формулу з-на Архимеда и выражение для объема вытесненной части шара, находим Т.
Записываем ответ.

Решение:

1. Переведем S и h в СИ: , . Плотность воды ρ равна:. 2. Поскольку шар полностью погружен в воду, то он вытесняет объем воду, равный собственному объему. Обозначим его V1. На погруженный шар действуют: сила тяжести mg, сила Архимеда FA1, сила натяжения Т.

3. После перерезания нити уровень воды в сосуде понизился, поскольку шар всплыл и теперь занимает в толще воды только часть своего объема, вытесняя меньше воды. Обозначим этот объем через V2. Объем части шара, оказавшегося над поверхностью воды, составляет

. Силы, действующие на шар: сила тяжести mg, сила Архимеда FT2.

4. В обеих ситуациях шар находится в равновесии. Поэтому по 3-му з-у Ньютона:

(1) – (2) :

Отсюда:

Ответ: 5 Н.

Первый вариант (Демидова, № 5)

На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 100 г и m2 = 400 г, связанные нерастяжимой невесомой нитью длиной l. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). При вращении штанги с частотой 900 об/мин модуль силы натяжения нити, соединяющей грузы, T = 150 Н. Определите длину нити l.

Алгоритм решения:

Определяем для каждого из грузов инерциальную с-му отсчета, в которой, применив 2-й з-н Ньютона, записываем уравнения в соответствующих проекциях.
Определяем вид ускорения и записываем формулы для его вычисления. Из предыдущих формул формируем уравнения для определения сил, действующих на грузы.
Анализируем соотношения между входящими в уравнения величинами и после преобразований выводим формулу для вычисления искомой длины.
Переводим в СИ несоответствующие ей значения из условия. Подставляем данные в результирующее уравнение, вычисляем длину нити.
Записываем ответ.

Решение:

1. Выбираем системы отсчета для каждого из грузов так, чтобы их оси были направлены горизонтально (вдоль штанги) от края штанги к оси вращения:

Т1 и Т2 на рисунке – силы, действующие соответственно на левый и правый грузы.

На основании 2-го з-на Ньютона запишем уравнения силы в проекции на оси с-м отсчета:

;

2. Т.к. в данном случае имеет место вращательное движение, то грузы испытывают центростремительное ускорение. Для их вычисления используем формулу:

, где w – угловая скорость их вращательного движения, R – радиусы окружностей их вращения. Поскольку , то применив эту и предыдущую формулы для каждого груза, получим: , . Подставим формулы для и в (1) и (2). Получим:

;

3. Если l – длина нити между грузами, то

. Выразим радиус вращения одного из грузов (например, правого) через радиус другого: .Поскольку грузы связаны в единую систему, то . Отсюда: (3)=(4) → . Учтя при этом (5), имеем: (6).

Приравняем Т к одной из сил, например:

. Приняв при этом во внимание (6), получаем: . Тогда: .

4. Переводим данные из условия в СИ:

; ; . Найдем l:

Ответ: 0,21 м.

Второй вариант (Демидова, № 11)

Алгоритм решения:

На основании условия чертим схему движения описанных объектов.
Используя з-н сохранения импульса, записываем уравнение для импульсов снаряда и осколков в проекции на ось Ох. Из него выразим модуль скорости для 2-го осколка (1).
Приняв во внимание, что кинет.энергия осколков (по условию) увеличилась на ∆Е, запишем уравнение, описывающее соотношение энергий снаряда и осколков. Отсюда выразим массу осколка (2).
Подставив (1) в (2) получим результирующее выражение для массы m.
Записываем ответ.

Решение:

1. Схема движения снаряд и его осколков выглядит так:

На схеме масса снаряда обозначена как 2m. Это следует из условия, что снаряд разорвался на равные части. Поскольку масса каждого из них составляет m, то их суммарная масса, являющаяся массой неразорвавшегося заряда, как раз и равна 2m. Обозначение на схеме «

» – это скорость второго осколка, движущегося в противоположную снаряду сторону. Обозначения вида mv – импульсы, соответствующие снаряду и паре осколков.

2. По з-ну сохранения импульса в момент разрыва снаряда

. Отсюда: .

3. Выразим взаимосвязь энергий до и после разрыва снаряда:

. Выполним преобразования и выразим m:

4. (1) → (2) :

Ответ:

Даниил Романович | ???? Скачать PDF | Просмотров: 2.9k | Оценить:

Источник