Два моля идеального газа находящегося в закрытом сосуде при
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 72.5%
Ответом к заданию 8 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Сосуд вместимостью 12 л, содержащий газ при давлении 0,4 МПа, соединяют с другим сосудом, из которого откачан воздух. Найдите конечное значение давления. Процесс изотермический. Вместимость второго сосуда равна 3,0 л. Ответ выразите в (МПа).
Решение
Дано:
$V_1=12·10^{-3}м^3$
$V_2=3·10^{-3}м^3$
$p_1=0.4·10^6$Па
$T_1=T_2=T=const$
$p_2-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2(V_2+V_1)}/{T_2}$(1), т.к. $T_1=T_2=T=const$, можно записать: $p_1V_1=p_2(V-2+V_1)$(2), откуда $p_2={p_1V_1}/{(V_2+V_1)}={0.4·10^6·12·10^{-3}}/{15·10^{-3}}=0.32$МПа.
Ответ: 0.32
Показать решение
Полный курс
Задача 2
Газ, занимающий объём 12,32 л, охладили при постоянном давлении на 45 К, после чего его объём стал равен 10,52 л. Какова была первоначальная температура газа? Ответ выразите в (К).
Решение
Дано:
$∆T=45K$
$V_1=12.32·10^{-3}м^3$
$V_2=10.52·10^{-3}м^3$
$p_1=p_2=p=const$
$T_1-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}$(1), учитывая, что $p=const$, имеем: ${pV_1}/{T_1}={pV_2}/{T_2}$ или $V_1T_2=V_2T_1$(2). Так как газ охладили, то $T_2=T_1-∆T$(3). Подставим (3) в (2): $V_1T_1-V_1∆T=V_2T_1⇒T_1={V_1∆T}/{(V_1-V_2)}={12.32·10^{-3}·45}/{1.8·10^{-3}}=308K$.
Ответ: 308
Показать решение
Полный курс
Задача 3
В закрытом сосуде находится 120 г газа при комнатной температуре. Какая масса газа вытечет из сосуда, если после открытия крана давление в сосуде понизится в 4 раза? Ответ выразите в (кг).
Решение
Дано:
$T=20+273=293К$
$P_2={P_1}/{4}$
$m_1=0.12$кг
$∆m-?$
$T=const$
$V=const$
Решение:
Зная уравнение Менделеева-Клайперона составим систему 1 и 2.
${tableP_1V={m}/{M}·RT_1; P_2V={m}/{M}·RT_2;$, то $4={m_1}/{m_2}; m_2=0.03$.
$∆m=m_1-m_2=0.12-0.03=0.09$кг.
Ответ: 0.09
Показать решение
Полный курс
Задача 4
В сосуде содержится неон при температуре −3◦С. Во сколько раз увеличится средняя кинетическая энергия теплового движения молекул неона, если его нагреть до 132◦С? В ответе запишите в(во) сколько раз(а).
Решение
Дано:
$t_1=-3+273=270К$
$T_2=132+273=405K$
${E_{к_2}}/{E_{к_1}}$
Решение:
$E_к={3}/{2}KT$.
${E_{к_2}}/{E_{к_1}}={T_2}/{T_1}={405}/{270}=1.5$
Ответ: 1.5
Показать решение
Полный курс
Задача 5
В сосуде содержится аргон при температуре 327◦С. Какая абсолютная температура установится, если концентрацию аргона увеличить в 2 раза, а давление уменьшить в 3 раза? Ответ выразить в (K).
Решение
Дано:
$T^1_{Ар}=327+273=600K$
$n_2=2·n_1$
$P_2={P_1}/{3}$
$T_2$
Решение:
Запишем уравнение состояния газа дважды:
${tableP_1=n_1·K·T_1; P_2=n_2·K·T_2;$ $⇒T_2={T_1}/{2}={600}/{6}=100K$.
Ответ: 100
Показать решение
Полный курс
Задача 6
В сосуде содержится водород, манометр показывает 0,5 атмосферы. Какое установится давление, если концентрацию водорода увеличить в 6 раз, а среднюю кинетическую энергию теплового движения его молекул уменьшить в 4 раза? Ответ выразите в (кПа).
Решение
Дано:
$P_1=0.5·P_{атм}$
$n_2=6·n_1$
$E_{к_2}={E_{к_1}}/{4}$
$P_{атм}=10^5$
Решение:
${tableP_1={2}/{3}·n_1·E_{к_1}; P_2={2}/{3}·n_2·E_{к_2};$ $⇒{0.5·10^5}/{P_2}={1}/{6}:{1}/{4}$.
Для 1 и 2 случая $P_2=75·10^3$Па.
Ответ: 75
Показать решение
Полный курс
Задача 7
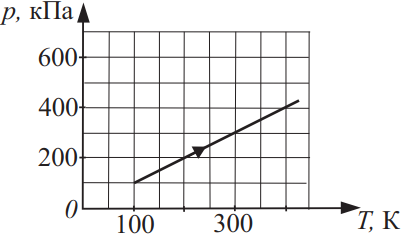
На рисунке показан график изменения давления 10 моль газа при изохорном нагревании. Найдите объём этого газа. Ответ округлите до целого, выразив в (дм3).
Решение
Дано:
$V-?$
$V=const$
$υ=10$моль
Решение:
Из уравнения Менделеева-Клайперона $pV=υRT⇒V={υRT}/{p}={10·8.31·100}/{100·10^3}=83.1дм^3$
Ответ: 83
Показать решение
Полный курс
Задача 8
1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 3 раза. Найдите первоначальную температуру газа. Ответ выразите в (К).
Решение
Дано:
$υ=1$моль
$υ=const$
$∆T=200K$
${P_1}/{3}=P_2$
$T_0-?$
Решение:
${P_1}/{T_1} > {P_2}/{T_2}$ – изохорный.
$T_0={P_1}/{P_2}·T_2=3(1-200)$
$2T_0=600$
$T_0=300K$
Ответ: 300
Показать решение
Полный курс
Задача 9
Определите плотность азота при температуре 27◦С и давлении 150 кПа. Ответ округлите до десятых. Ответ выразите в (кг/м3).
Решение
Дано:
$T=27°C=300K$
$P=150$кПа
$v=2(Т_2)$
$ρ-?$
Решение:
$PV={m}/{M}·RT$
$ρ·R·T=P·M$
$ρ={P·M}/{R·T}={150·10^3·0.028}/{8.31·300}=1.7кг/м^3$.
Ответ: 1.7
Показать решение
Полный курс
Задача 10
Определите температуру азота, имеющего массу 4 г, занимающего объём 831 см3 при давлении 0,2 МПа. Ответ выразите в (К).
Решение
Дано:
$N_2T-?$
$m=4·10^{-3}кг$
$V=831см^3$
$P=0.2·10^6$
$T_?$
Решение:
По закону Менделеева-Клайперона $pV={m}/{M}R·T; T={pv·M}/{m·R}$
$T={0.2·10^6·8.31·0.028}/{4·10^{-3}·8.31}=140K$
Ответ: 140
Показать решение
Полный курс
Задача 11
При повышении температуры идеального газа на 100 К среднеквадратичная скорость движения молекул выросла с 200 м/с до 600 м/с. Насколько надо понизить температуру газа, чтобы среднеквадратичная скорость уменьшилась с 600 м/с до 400 м/с? В ответе запишите на сколько (K).
Решение
Дано:
$∆T=100K↑$
$υ_{cр_1}=200$м/с
$υ_{cр_2}=600$м/с
$∆T-?↓$
$υ_{cр_2}=600$м/с
$υ_{cр_3}=400$м/с
Решение:
В первом процессе $T_1={υ_1^2μ}/{3R}$
$T_2={υ_2^2μ}/{3R}$
$∆T_1=T_2-T_1={μ}/{3R}·(υ_2^2·r_1^2)$
${μ}/{3R}={∆T}/{υ_2^2-r_1^2}={1}/{3200}$
Тогда $∆T_2={μ}/{3R}(υ_2^2-υ_3^2)={1}/{3200}(400^2-600^2)=62.5K$
Ответ: 62.5
Показать решение
Полный курс
Задача 12
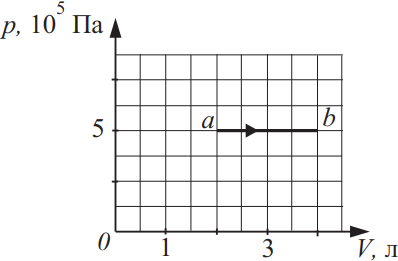
Идеальный газ в количестве 1,5 моль совершает процесс, изображённый на рисунке. Какова температура газа в состоянии b? Ответ выразите в (K), округлив до сотых.
Решение
Дано:
$v=1.5$моль
$T_в-?$
$P=const=10^5$Па
$V_a=2л$
$V_в=4л$
Решение:
По закону Менделеева-Клайперона для точки а и в составим систему: ${tableP·V_a=vRT_a(1); P·V_в=vRT_в(2);$. Из (2) найдем: $T_в={5·10^5·4·10^{-3}}/{1.5·8.31}=160.45K$
Ответ: 160.45
Показать решение
Полный курс
Задача 13
Концентрация молекул идеального одноатомного газа равна 2 · 1024 м−3. Какое давление оказывает газ на стенки сосуда, если при этом средняя кинетическая энергия молекулы равна 1,5 · 10−20 Дж? Ответ выразите в (кПа).
Решение
Дано:
$n=2·10^{24}м^{-3}$
$E_к=1.5·10^{-20}$
$P-?$
Решение:
${tableE_к={3}/{2}KT={3}/{2}K{P}/{nK}; P=nKT;$
Выразим и получим формулу из основ МКТ: $p={E_к·2n}/{3}={1.5·10^{-20}·2·2·10^{24}}/{3}=20$кПа.
Ответ: 20
Показать решение
Полный курс
Задача 14
Температура идеального газа понизилась от 700◦С до 350◦С. Во сколько раз при этом изменилась средняя кинетическая энергия движения молекул газа? Ответ округлить до сотых
Решение
Дано:
$T_1=700°C+273=973K$
$T_2=350°C+273=623K$
${E_1}/{E_2}-?$
Решение:
Из основ молекулярно-кинетической теории известно, что ${E_1}/{E_2}={T_1}/{T_2}$
${E_1}/{E_2}={973}/{623}=1.56$
Ответ: 1.56
Показать решение
Полный курс
Задача 15
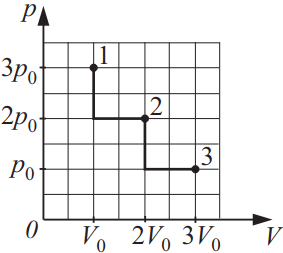
На диаграмме pV изображены процессы перевода некоторой неизменной массы идеального газа из состояния 1 в состояние 3. Начальная (T1) и конечная (T3) температуры связаны между собой соотношением T3/T1…
Решение
Дано:
$Т_1-$начальная
$Т_2$конечная
${T_3}/{T_1}-?$
Решение:
Запишем уравнение Менделеева-Клайперона для начальной и конечной точки состояния: ${table.{p_1·V_1}/{T_1}=υR; .{p_3·V_3}/{T_3}=υR;$.
$⇒{p_1·V_1}/{T_1}={p_3·V_3}/{T_3}⇒{T_3}/{T_1}={p_3·V_3}/{p_1·V_1}⇒{T_3}/{T_1}={p_0·3V_0}/{3p_0·V_0}=1$.
Ответ: 1
Показать решение
Полный курс
Задача 16
При какой температуре молекулы гелия имеют такую же среднюю квадратичную скорость, как молекулы водорода при 27◦С? Ответ выразите в (◦ С).
Решение
Дано:
$t_{H_2}=27°C$
$_{He}=_{H_2}$
$t_{He}-?$
Решение:
Средняя квадратичная скорость молекул гелия и водорода ($He$ и $H_2$) равны соответственно: $_{He}=√{{3RT_{He}}/{μ_{He}}}$, где $T_{He}=t_{He}+273°C$
$_{H_2}=√{{3RT_{H_2}}/{μ_{H_2}}}$, где $T_{H_2}=t_{H_2}-273°C$
Молярные массы гелия $He$ и водорода $H_2$ равны соответственно: $μ_{He}=4·10^{-3}кг/моль; μ_{H_2}=2·10^{-3}кг/моль; T_{H_2}=27°C+273°C=300K$
$√{{3RT_{He}}/{μ_{He}}}=√{{3RT_{H_2}}/{μ_{H_2}}}⇒{3RT_{He}}/{μ_{He}}={3RT_{H_2}}/{μ_{H_2}}⇒T_{He}={T_{H_2}·μ_{He}}/{μ_{H_2}}={300·4·10^{-3}}/{2·10^{-3}}=600K$, тогда $t_{He}=T_{He}-273°C=600°C-273°C=327°C$
Ответ: 327
Показать решение
Полный курс
Задача 17

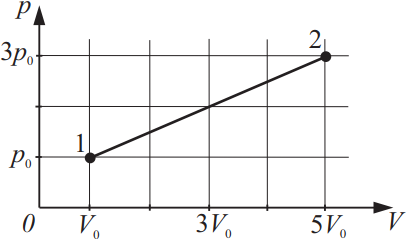
На рисунке изображено изменение состояния идеального газа. Во сколько раз температура в состоянии 2 больше, чем температура в состоянии 1?
Решение
Дано:
$p_1=p_0$
$V_1=V_0$
$p_2=3p_0$
$V_2=5V_0$
${T_2}/{T_1}-?$
Решение:
Из уравнения Менделеева-Клайперона: $pV={m}/{μ}RT$(1), следует равенство ${p_1V_1}/{T_1}={p_2V_2}/{T_2}⇒{p_0V_0}/{T_1}={3p_0·5V_0}/{T_2}$(2).
Из (2) имеем: $p_0V_0T_2=3p_0V_0·5T_1$
$T_2=3·5T_1⇒T_2=15T_1$ или ${T_2}/{T_1}=15$
Ответ: 15
Показать решение
Полный курс
Источник
8. Молекулярно-кинетическая теория
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
В сосуде объёмом 2 л находится 10 г идеального газа при давлении 1 атм. и температуре 300 К. Во втором сосуде объёмом 4 л находится 20 г того же газа при давлении 2 атм. Чему равна температура газа во втором сосуде? (Ответ дайте в кельвинах.)
Уравнение состояния газа: [pV=nu RT=dfrac{m}{mu}RT] где (p) — давление газа, (V) — объем, занимаемый газом, (nu) — количество вещества, (R) — универсальная газовая постоянная, (T) — температура газа, (m) — масса газа, (mu) — молярная масса газа.
Для первого сосуда: [p_1V_1=dfrac{m_1}{mu}RT_1] Для второго сосуда: [p_2V_2=dfrac{m_2}{mu}RT_2] Поделим уравнения друг на друга: [dfrac{p_1V_1}{p_2V_2}=frac{m_1T_1}{m_2T_2}] [T_2=T_1cdotdfrac{m_1}{m_2}cdotdfrac{V_2}{V_1}cdotdfrac{p_2}{p_1}=300text{ К}cdotdfrac{1}{2}cdot2cdot2=600 text{ К}]
Ответ: 600
При уменьшении абсолютной температуры газа на 300 К давление уменьшилось в 5 раз. Какова начальная температура газа, если в ходе эксперимента количество вещества уменьшилось втрое, а объём оставался постоянным? (Ответ дайте в кельвинах.)
Запишем уравнение Менделеева-Клапейрона для первого и второго состояния: [begin{cases}
p_1 V=nu_1 R T_1\
p_2 V=nu_2 R T_2
end{cases}] где (p_1) и (p_2) — давления газа в первом и втором состояниях, V — объём газа, (nu_1) и (nu_2)— количество вещества в первом и втором состояниях, (R) — универсальная газовая постоянная, (T_1) и (T_2) — абсолютная температура в первом и втором состояниях.
Поделив одно уравнение на другое, получим: [dfrac{p_1}{p_2} = dfrac{nu_1 T_1}{nu_2 T_2}] Так как (nu_1 = 3nu_2) и (p_1 = 5p_2), то: [dfrac{5p_2}{p_2} = dfrac{3nu_2cdot T_1}{nu_2cdot T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5=dfrac{3T_1}{T_2}
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_2 = 3T_1] Так как (T_2 = (T_1 – 200) К), то: [5(T_1 – 300text{ K}) = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
5T_1 – 1500text{ K } = 3T_1
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
2T_1 = 1500text{ K }
hspace{0,4 cm} Rightarrow hspace{0,4 cm}
T_1 = 750text{ K }]
Ответ: 750
На графиках приведены зависимости давления (p) и объема (V) от времени (t) для 1 моля идеального газа. Чему равна температура газа в момент (t) = 30 минут? (Ответ дайте в градусах Кельвина с точностью до 10 К.)
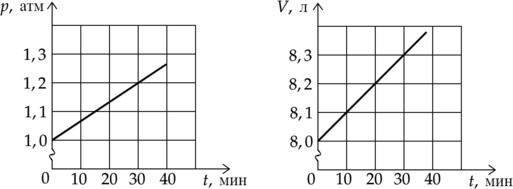
Уравнение состояния идеального газа: [displaystyle pV=nu RT,] где (p)—давление газа, (V)—объем газа, (nu) — количество вещества газа, (R) — универсальная газовая постоянная, (T) — температура. Выразим температуру газа: [T=dfrac{pV}{nu R}] Из графика найдем давление и объем в момент времени 30 мин:
(p=1,2cdot10^5) Па
(V=8,3cdot10^{-3}text{ м$^3$})
Подставим известные и найденные значения в формулу: [T=dfrac{1,2cdot10^5text{ Па}cdot8,3cdot10^{-3}text{ м$^3$}}{1text{ моль}cdot8,31text{ }dfrac{text{Дж}}{text{моль}}} approx 120 text{ К}]
Ответ: 120
В сосуде неизменного объёма находится разреженный газ в количестве 3 моль. Во сколько раз изменится давление газа в сосуде, если выпустить из него 1 моль газа, а абсолютную температуру газа уменьшить в 2 раза?
“Демоверсия 2019”
Запишем уравнение Клапейрона – Менделеева: [p1V=nu_1RT_1=3RT_1] [p_2V=nu_2RT_2=2Rdfrac{T_1}{2}=RT_1] [dfrac{p_1}{p_2}=dfrac{3RT_1}{RT_1}=3]
Ответ: 3
В сосуде неизменного объёма находится идеальный газ. Во сколько раз нужно увеличить количество газа в сосуде, чтобы после уменьшения абсолютной температуры газа в 2 раза его давление стало вдвое больше начального?
“Досрочная волна 2020 вариант 1”
Из уравнения Клапейрона –Менделеева: [pV=nu RT] чтобы давление ((p)) увеличилось в 2 раза, при уменьшении температуры ((T)) в 2 раза, количество вещества ((nu)) должно увеличится в 4 раза
Ответ: 4
В сосуде неизменного объема находится разреженный газ в количестве 4 моль. Во сколько раз нужно увеличить абсолютную температуру газа, чтобы после удаления из сосуда 3 моль газа, давление осталось неизменным?
“Основная волна 2020 ”
Уравнение Клайперона – Менделеева: [pV=nu RT] если удалить 3 моль газа, то количество вещества уменьшится в 4 раза (nu_1=dfrac{nu}{4}), следовательно, температуру надо увеличить в 4 раза.
Ответ: 4
Источник
Изобарный процесс
Заполните пропуск в тексте.
Повторите определение изобарного процесса.
Процесс изменения состояния термодинамической системы данной массы при называют изобарным.
постоянном давлении
постоянной температуре
постоянном объёме
Газовые законы
Заполните таблицу.
Повторите газовые законы.
| Закон | Изопроцесс | Формула |
|---|---|---|
$frac{V}{T}=const$ | ||
Изотермический | ||
Шарля |
Изохорный
Гей-Люссака
Бойля–Мариотта
$pV=const$
$frac{p}{T}=const$
Изобарный
Физические величины
Установите соответствие между физическими величинами и их единицами измерения.
Вспомните основные величины и единицы их измерения.
Уравнение состояния идеального газа
Соедините попарно физическую величину с её значением так, чтобы получились верные ответы.
1. В баллоне объёмом 2 $м^3$ находится 2 кг молекулярного кислорода при давлении $10^5$ Па. Какова температура кислорода (ответ в К)?
2. В баллоне ёмкостью 10 л находится углекислый газ при температуре 17 $^circ$ С под давлением 107 Па. Какой объём займёт этот газ при нормальных условиях (ответ в $м^3$)?
3. В закрытом сосуде объёмом 10 литров находится 2 моль азота. Температура газа равна 27 $^circ$ С. Чему равно давление газа (ответ в кПа)?
Повторите уравнение состояния идеального газа.
Изопроцессы
Соедините попарно фигуры так, чтобы каждому изопроцессу соответствовала формула.
Вспомните определения изопроцессов.
Основные величины МКТ
Решите кроссворд.
Вспомните основные величины МКТ и единицы их измерения.
Физические термины
Выделите мышкой 5 слов, которые относятся к теме урока.
1. Состояние вещества, в котором расстояние между атомами и молекулами в среднем во много раз больше размеров самих молекул.
2. Мельчайшая частица вещества.
3. Итальянский учёный XIX века, в честь которого названа постоянная, показывающая, какое количество атомов или молекул содержится в 1 моле вещества.
4. Синоним слова «корпускула».
5. Единица измерения количества вещества в СИ.
Повторите авторов законов и определения.
Газовые законы
Заполните пропуски в тексте, выбрав правильные варианты ответа из выпадающего меню.
Повторите газовые законы.
В сосуде под поршнем находится газ. При его изотермическом расширении давление газа на стенки сосуда
, температура
, объём газа
.
Измерительные приборы
Установите соответствие между физическими величинами и приборами для их измерения.
Повторите определения давления, температуры.
Экспериментальные исследования
Выберите верные утверждения, которые соответствуют результатам проведённых экспериментальных исследований.
В сосуде неизменного объема при комнатной температуре находилась смесь водорода и гелия, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль водорода. Газы считаются идеальными, а их температура постоянной.
Вспомните закон Гей-Люссака, закон Дальтона, определение парциального давления.
Парциальное давление водорода уменьшилось
В начале опыта массы газов были одинаковые
В начале опыта концентрации газов были одинаковые
Концентрация гелия увеличилась
Давление смеси газов в сосуде не изменилось
Изотермический процесс
На рисунке приведены графики двух изотермических процессов, проводимых с одной и той же массой газа. На основании графиков выберите верные утверждения о процессах, происходящих с газом.

Вспомните график изотермического процесса, на графике посмотрите направление стрелки.
Процесс 2 идёт при более высокой температуре
Процесс 1 идёт при более высокой температуре
В процессе 1 объём увеличивается
Никаких выводов по графику сделать нельзя
Оба процесса идут при одной и той же температуре
Газовые законы
Выделите мышкой 5 слов, которые относятся к теме урока.
1. Один из учёных, открывших изотермический процесс.
2. Единица измерения абсолютной температуры.
3. Параметр состояния газа постоянный в изохорном процессе.
4. Процессы, происходящие при постоянном значении одного из макропараметров состояния
5. Параметр состояния газа постоянный в изотермическом процессе.
Вспомните газовые законы.
Изопроцессы
Выделите мышкой 4 слова, которые относятся к теме урока.
1. Макроскопический параметр постоянный во всех изопроцессах.
2. Величины, характеризующие состояние газа.
3. График изопроцесса с постоянным объёмом.
4. График изопроцесса с постоянным давлением.
Вспомните изопроцессы.
Газовые законы
Выделите мышкой 4 слова, которые относятся к теме урока.
1. То, из чего состоит молекула.
2. Масса моля вещества.
3. Упрощённая модель реального газа.
4. Учёный, открывший взаимосвязь между давлением и температурой при постоянном объёме.
Повторите конспекты.
Источник
