Два одинаковых сосуда содержащие одинаковое число атомов гелия
Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 7196
$N$ атомов газообразного гелия находятся при комнатной температуре в кубическом сосуде, объем которого равен $1,0 см^{3}$. Найти:
а) вероятность того, что все атомы соберутся в одной половине сосуда;
б) примерное числовое значение $N$, при котором это событие можно ожидать на протяжении времени $t approx 10^{10}$ лет (возраст Вселенной).
Подробнее
Задача по физике – 7197
Найти статистический вес наиболее вероятного распределения $N = 10$ одинаковых молекул по двум одинаковым половинам сосуда. Определить также вероятность такого распределения?
Подробнее
Задача по физике – 7198
$N$ молекул идеального газа находятся в некотором сосуде. Разделим мысленно сосуд на две одинаковые половины А и В. Найти вероятность того, что в половине А сосуда окажется $n$ молекул. Рассмотреть случаи, когда $N = 5$ и $n = 0, 1, 2, 3, 4, 5$.
Подробнее
Задача по физике – 7199
В сосуде объемом $V_{0}$ находится $N$ молекул идеального газа. Найти вероятность того, что в некоторой выделенной части этого сосуда, имеющей объем $V$, окажется $n$ молекул. Рассмотреть, в частности, случай $V = V_{0}/2$.
Подробнее
Задача по физике – 7200
Идеальный газ находится при нормальных условиях. Найти диаметр сферы, в объеме которой относительная флуктуация числа молекул $eta = 1,0 cdot 10^{-3}$. Каково среднее число молекул внутри такой сферы?
Подробнее
Задача по физике – 7201
Один моль идеального газа, состоящего из одноатомных молекул, находится в сосуде при температуре $T_{0} = 300 К$. Как и во сколько раз изменится статистический вес этой системы (газа), если ее нагреть изохорически на $Delta T = 1,0 К$?
Подробнее
Задача по физике – 7202
Найти капиллярное давление:
а) в капельках ртути диаметра $d = 1,5 мкм$;
б) внутри мыльного пузырька диаметра $d = 3,0 мм$, если поверхностное натяжение мыльной воды $alpha = 45 мН/м$.
Подробнее
Задача по физике – 7203
В дне сосуда со ртутью имеется круглое отверстие диаметра $d = 70 мкм$. При какой максимальной толщине слоя ртути она еще не будет вытекать через это отверстие?
Подробнее
Задача по физике – 7204
В сосуде с воздухом при давлении $p_{0}$ находится мыльный пузырек диаметра $d$. Давление воздуха изотермически уменьшили в $n$ раз, в результате чего диаметр пузырька увеличился в $eta$ раз. Найти поверхностное натяжение мыльной воды.
Подробнее
Задача по физике – 7205
Найти давление в пузырьке воздуха диаметра $d = 4,0 мкм$, который находится в воде на глубине $h = 5,0 м$. Атмосферное давление $p_{0}$ нормальное.
Подробнее
Задача по физике – 7206
На дне пруда выделился пузырек газа диаметра $d = 4,0 мкм$. При поднятии этого пузырька к поверхности воды его диаметр увеличился в $n = 1,1$ раза. Найти глубину пруда, в данном месте. Атмосферное давление нормальное, процесс расши рения газа считать изотермическим.
Подробнее
Задача по физике – 7207
Найти разность уровней ртути в двух сообщающихся вертикальных капиллярах, диаметры которых $d_{1} = 0,50 мм$ и $d_{2} = 1,00 мм$, если краевой угол $theta = 138^{ circ}$.
Подробнее
Задача по физике – 7208
Вертикальный капилляр с внутренним диаметром 0,50 мм погрузили в воду так, что длина выступающей над поверхностью воды части капилляра оказалась $h = 25 мм$. Найти радиус кривизны мениска.
Подробнее
Задача по физике – 7209
Стеклянный капилляр длины $l = 110 мм$ с диаметром внутреннего канала $d = 20 мкм$ опустили в вертикальном положении в воду. Верхний конец капилляра запаян. Наружное давление воздуха нормальное. Какая длина $x$ капилляра должна быть погружена в воду, чтобы уровень воды в капилляре совпадал с поверхностью воды вне его?
Подробнее
Задача по физике – 7210
Вертикальный капилляр длины $l$ с запаянным верхним концом привели в соприкосновение с поверхностью жидкости, после чего она поднялась в нем на высоту $h$. Плотность жидкости $rho$, диаметр сечения внутреннего канала капилляра $d$, краевой угол $theta$, атмосферное давление $p_{0}$. Найти поверхностное натяжение жидкости.
Подробнее
Источник
Решениие задач по химии на закон Авогадро
Задача 53.
Сопоставить числа молекул, содержащихся в 1г NH3 и в 1г N2. В каком случае и во сколько раз число молекул больше?
Решение:
В одном моле любого вещества содержится 6,02 . 1023 молекул этого вещества.
Рассчитаем содержание количества вещества в 1г NH3 и N2 по формуле:
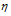(B) – количество вещества (В);
m(B)- масса вещества (В);
M(B) – Молярная масса вещества (В).
М(NH3) = 17г/моль, M(N2) = 28г/моль.
Тогда
Число молекул NH3 больше числа молекул N2, так как 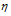(NH3) >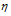(N2) . Теперь рассчитаем, во сколько раз число молекул NH3 больше числа молекул N2:
Ответ: в 1,65 раз число молекул NH3 больше числа молекул N2.
Задача 54.
Выразить в граммах массу одной молекулы диоксида серы.
Решение:
Находим молекулярную массу диоксида серы:
M(SO2) = 32 + (16 . 2) = 64г/моль.
Молекулярная масса численно составляет массу одного моля вещества, а значит, вес одного моля численно равен молекулярной массе и составляет 64г. Известно, что в одном моле любого вещества содержится 6,02 . 1023 молекул данного вещества. Исходя из этого, рассчитаем массу в граммах одной молекулы диоксида серы:
Ответ: масса одной молекулы диоксида серы равна.
Задача 55.
Одинаково ли число молекул в 0,001кг Н2 и в 0,001кг О2? В 1 моле Н2 и в 1 моле 02? В 1л Н2 и в 1л О2 при одинаковых условиях?
Решение:
Молекулярные массы водорода и кислорода равны соответственно 2г/моль и 32г/моль. Отсюда находим количество водорода и кислорода, зная их массы:
Один моль любого вещества содержит 6,02 .1023 молекул. Следовательно, в 0,001кг водорода и в 0,001кг кислорода содержится разное число молекул:
Так как имеется по одному молю водорода и кислорода, то количество молекул веществ будет одинаково:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л, В которых содержится 6,02 . 1023 молекул. Отсюда рассчитаем количество молекул вещества, содержащихся в 1л водорода и в 1л кислорода:
Ответ: а) в 0,001кг водорода и в 0,001кг кислорода содержится разное число молекул; б) в одном моле водорода и в одном моле кислорода содержится одинаковое число молекул: в) в одном литре водорода и в одном литре кислорода содержится одинаковое число молекул.
Задача 56.
Сколько молекул содержится в 1,00 мл водорода при нормальных условиях?
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л, В которых содержится 6,02 .1023 молекул. Отсюда рассчитаем количество молекул вещества, содержащихся в 1мл водорода из пропорции:
Ответ: 2,69 .1019 молекул.
Задача 57.
Какой объем при нормальных условиях занимают 27 .1021 молекул газа?
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л, В которых содержится 6,02 . 1023 молекул. Отсюда находим какой объём при нормальных условиях занимают 27 .1021 молекул газа, составив пропорцию:
Ответ: V=1л.
Задача 58.
Каково соотношение объемов, занимаемых 1 молем О2 и 1 молем О3 (условия одинаковые)?
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л. Следовательно соотношение объёмов, занимаемых одним молем О2 и одним молем О3 иметь вид:
Ответ: 1:1
Задача 59.
Взяты равные массы кислорода, водорода и метана при одинаковых условиях. Найти отношение объемов взятых газов.
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л. Мольные массы кислорода, водорода и метана, соответственно равны 32 г/моль; 2г/моль; 16 г/моль.
Так как массы кислорода, водорода и метана одинаковы при одинаковых условиях, то отношение объёмов взятых газов находим из пропорции:
Ответ: 1:16:2.
Задача 60.
На вопрос, какой объем займет 1моль воды при нормальных условиях, получен ответ: 22,4л. Правильный ли это ответ?
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л. Так как вода при нормальных условиях находится в жидкой, а не в газообразной фазе, то ответ, что 1моль воды займёт 22,4л не правильный. Учитывая, что молярная масса воды равна 18г/моль, а плотность равна единице, то правильный ответ будет равен:
Ответ: 18мл.
Задача 61.
Сколько молекул диоксида углерода находится в 1л воздуха, если объемное содержание СО2 составляет 0,03% (условия нормальные)?
Решение:
При нормальных условиях углекислый газ, содержащийся в 1л воздуха, занимает объём 0,0003л. Зная, что мольный объём любого газа занимает 22,4л, рассчитаем число молей углекислого газа в 0,0003л из пропорции:
Учитывая, что в одном моле вещества содержится 6,02 . 1023 молекул, находим число молекул в 0,0003л газа:
Ответ: 8,07 .1018 молекул.
Источник
Тема. Решение задач по теме «Скорости газовых молекул. Распределение молекул по скоростям »
Цели
На примерах решения задач познакомить учащихся с основными типами задач и методами их решения.
Ход занятия
Вспомните основные свойства модели идеального газа. Повторите понятие размера молекул и длины свободного пробега. Выведите формулу для длины свободного пробега. Покажите, что длина свободного пробега зависит от давления, под которым находится газ. Подсчитайте число молекул, находящихся в единице объема при нормальных условиях. Обсудите насколько велико это число.
Качественные вопросы
1. Какие гипотезы положены в основу вывода основного уравнения молекулярно-кинетической теории газа?
2. Как правильно сформулировать вопрос о распределении молекул по скоростям?
3. Какой физический смысл имеет функция распределения молекул по скоростям?
4. Чему равна ограниченная кривой распределения молекул по скоростям площадь?
5. Как изменяются с температурой положение максимума кривой функции распределения молекул по скоростям и его высота?
Примеры решения задач
Задача 1.Найти среднюю длину свободного пробега молекул воздуха при нормальных условиях. Эффективный диаметр молекул принять равным м.
Решение
Средняя длина свободного пробега определяется формулой , где r – радиус молекулы. Так как d = 2r, то , где – число молекул в единице объема, Р – давление и Т – температура. Подставляя значение в формулу для длины свободного пробега, получим
м.
Ответ: м.
Задача 2. Найти среднюю длину свободного пробега атомов гелия в условиях, когда плотность гелия ρ = 2,1·10–2 кг/м3, а эффективный диаметр атома гелия d = 1,9·10–2 м.
Решение
Для определения средней длины свободного пробега необходимо знать концентрацию молекул n при данных условиях. Найдем n0. Из уравнения Клапейрона–Менделеева следует, что
.
Следовательно,
.
И для средней длины свободного пробега l получаем расчетную формулу
м.
Ответ: м.
Задача 3. Какое предельное число молекул азота может находиться в сферическом сосуде диаметром D = 1 см, чтобы молекулы не сталкивались друг с другом? Диаметр молекул азота d = 3,1·10–10 м.
Решение
Для того чтобы столкновений молекул друг с другом не было, необходимо чтобы средняя длина свободного пробега λ была не меньше диаметра сосуда D, то есть λ ≥ D. Известно, что
,
где d – эффективный диаметр молекул азота, n – число молекул в единице объема, то есть концентрация молекул. Зная d, можно найти допустимую концентрацию молекул.
.
Максимальное число молекул в сосуде, объем которого , определится следующим образом
.
Ответ: .
Задача 4. Азот находится под давлением Па при температуре Т = 300 К. Найти относительное число молекул азота, скорости которых лежат в интервале скоростей, отличающихся от наиболее вероятной на Δv = 1 м/с.
Решение
Так как интервал скоростей Δv мал, то изменением функции распределения в этом интервале скоростей можно пренебречь, считая ее приближенно постоянной.
.
Подставляем значение наиболее вероятной скорости
;
.
Это и есть решение задачи. Производим вычисления: масса молекулы азота кг, постоянная Больцмана Дж/К. Подставляя численные значения, получим
.
При подсчете необходимо учесть, что определяется относительное число молекул, отличающихся по скорости от наиболее вероятной в обе стороны, то есть интервал равен Δv = 2 м/с.
Ответ: .
Задача 5. Найти температуру газообразного азота, при которой скоростям молекул v1 = 300 м/с и v2 = 600 м/с соответствуют одинаковые значения функции распределения Максвелла молекул по скоростям.
Решение
Запишем функцию распределения для указанных скоростей. По условию задачи значения функции должны быть одинаковы.
;
;
;
;
.
Масса молекулы азота кг.
Постоянная Больцмана Дж/К.
К.
Ответ: = 300 К.
Задача 6. Найти отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах.
Решение
Воспользуемся формулой для определения средней квадратичной скорости
,
где – молярная масса газа. Тогда отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах будет равно
,
где- молярная масса неона, – молярная масса гелия. Подставляя численные значения, получим
Ответ: .
Задача 7. Определить: 1) число молекул в 1 мм3 воды, 2) массу молекулы воды, 3) диаметр молекулы воды, считая условно, что молекулы воды шарообразны и соприкасаются.
Решение
Число молекул, содержащихся в массе вещества равно числу Авогадро , умноженному на число молей (- молярная масса вещества)
,
где r – плотность, V – объем вещества. После подстановки числовых значений получим
.
Массу m1 одной молекулы можно определить, разделив массу одного моля на число Авогадро:
кг.
Считая, что молекулы соприкасаются, объем, занимаемый одной молекулой , где d – диаметр молекулы. Отсюда . Так как , где – объем одного моля, то
м.
Ответ: ; кг; м.
Задача 8. Зная, что диаметр молекулы кислорода d = 3·10–10 м подсчитать, какой длины S получилась бы цепочка из молекул кислорода, находящихся в объеме V = 2 см2 при давлении Р = 1,01·105 Н/м2 и температуре Т = 300 К, если эти молекулы расположить вплотную в один ряд. Сравнить длину этой цепочки со средним расстоянием от Земли до Луны м.
Решение
Число молекул кислорода, содержащихся в единице объема, согласно основному уравнению молекулярно-кинетической теории, равно
,
Число молекул в объеме V будет равно . Следовательно, м.
Тогда .
Ответ: м; раз.
Задача 9. Средняя квадратичная скорость молекул некоторого газа vc.к. = 450 м/с. Давление газа р = 7 · 104 Н/м2. Найти плотность газа ρ при этих условиях.
Решение
Из уравнения Клайперона–Менделеева следует: . Учитывая, что , получаем .
Ответ: .
Задания для самостоятельной работы
1. В опыте Штерна источник атомов серебра создает пучок, который падает на внутреннюю поверхность неподвижного цилиндра радиуса R = 30 см и образует на ней пятно. Цилиндр начинает вращаться с угловой скоростью ω = 100 рад/с. Определить скорость атомов серебра, если пятно отклонилось на угол φ = 0,314 рад от первоначального положения.
Ответ: м/с.
2. Сколько молекул газа содержится в баллоне емкостью V = 60 л при температуре Т = 300 К и давлении P= 5·103 Н/м2?
Ответ: .
3. Определить температуру газа, для которой средняя квадратичная скорость молекул водорода больше их наиболее вероятной скорости на Δv = 400 м/с. Масса молекулы водорода т = 3,35·10–27 кг.
Ответ: = 380 К.
4. Вычислить среднее расстояние между центрами молекул идеального газа при нормальных условиях.
Ответ: м.
5. В помещении площадью S = 100 м2 и высотой h = 4 м разлито V1 = 1 л ацетона (СН3)2СО. Сколько молекул ацетона содержится в 1 м3 воздуха, если весь ацетон испарился? Плотность r ацетона 792 кг/м3.
Ответ:
6. Найти число столкновений z, которые произойдут за 1 с в 1 см3 кислорода при нормальных условиях. Эффективный радиус молекулы кислорода принять равным
1,5·10–10 м.
Ответ: .
7. Найти среднюю длину свободного пробега молекул азота при давлении P = 133 Па и температуре t = 27°C.
Ответ: м.
8. Доказать, что средняя арифметическая и средняя квадратичная скорости молекул газа пропорциональны , где P – давление газа; ρ – плотность газа.
Ответ: .
9. Два одинаковых сосуда, содержащие одинаковое число молекул кислорода, соединены краном. В первом сосуде средняя квадратичная скорость молекул равна , во втором – . Какой будет эта скорость, если открыть кран, соединяющий сосуды (теплообмен с окружающей средой отсутствует)?
Ответ: .
Рекомендуемая литература
1. Бутиков Е.И., Кондратьев А.С. Физика. Т.3. Строение и свойства вещества – Москва – Санкт-Петербург. Физматлит. Невский диалект. Лаборатория Базовых Знаний, 2001. С. 170-194.
2. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А., Цвецинская Т.С. Задачник по физике – Москва. Физматлит, 2005.
3. Готовцев В.В. Лучшие задачи по механике и термодинамике. Москва-Ростов-на-Дону, Издательский центр «Март», 2004. С. 215-219.
Источник