Два одинаковых сосуда соединены трубкой система наполнена газом
Опубликовано ср, 07/17/2019 – 21:59 пользователем fizportal.ru
ОСНОВЫ МКТ. Идеальный газ. Закон Дальтона. Тема 13-3
13.43. Внутри нетеплопроводного цилиндра, расположенного горизонтально, имеется тонкий нетеплопроводный подвижный поршень. На каких расстояниях L1 и L2 от оснований цилиндра расположен поршень, если с одной стороны от поршня в цилиндре находится кислород при температуре 127 °С, а с другой водород при температуре 27 °С? Массы обоих газов одинаковы. Общая длина цилиндра L = 65 см.
13.44. Два сосуда, содержащие одинаковые массы одного и того же газа, соединены трубкой с краном. В первом сосуде давление газа 4,0 кПа, а во втором 6,0 кПа. Какое давление p установится в системе после открывания крана? Температура газа постоянна.
13.45. Два сосуда соединены трубкой с краном. В первом сосуде находится масса 2,0 кг газа под давлением 4,0 × 105 Па, а во втором – 3,0 кг того же газа под давлением 9,0 × 105 Па. Какое давление p установится в системе после открывания крана? Температура газа постоянна.
13.46. Для приготовления газовой смеси с общим давлением p = 5,0 гПа к сосуду объема V = 10 л подсоединили баллон объема V1 = 1,0 л, в котором находился гелий под давлением p1 = 40 гПа, и баллон с неоном под давлением p2 = 10 гПа. Найдите объем V2 баллона с неоном. Температуры газов одинаковы и постоянны.
13.47. Два одинаковых сосуда соединены трубкой, объемом которой можно пренебречь. Система наполнена газом под давлением po. Во сколько n раз нужно изменить температуру газа в одном из сосудов, чтобы давление во всей системе стало равным p1?
13.48. Определите плотность $rho$ смеси, содержащей 4 г водорода и 32 г кислорода при температуре 7 °С и общем давлении 1,0 × 105 Па.
13.49. В сосуде находится смесь трех газов с массами m1, m2, m3 и с известными молярными массами μ 1, μ 2, μ 3. Определите плотность $rho$ смеси, если ее давление p и температура T известны.
Ответ
$rho$ = (m1 + m2 + m3)p/{(m1/μ1 + m2/μ2 + m3/μ3)RT}
13.50. Сосуд объема 2V = 200 см3 разделен на две равные части полупроницаемой неподвижной перегородкой. В первую половину сосуда введена смесь 2 мг водорода и 4 мг гелия, во второй половине вакуум. Через перегородку может диффундировать только гелий. Во время процесса поддерживается температура T = 300 К. Какие давления p1 и p2 установятся в обеих частях сосуда?
13.51. Сосуд объема V = 2 дм 3 разделен на две равные части полупроницаемой неподвижной перегородкой. В первую половину сосуда введена смесь 2 г водорода и 20 г аргона, во второй половине – вакуум. Через перегородку может диффундировать только водород. Во время процесса поддерживается температура t = 20 °C. Какое давление p установится в первой части сосуда? Молярная масса аргона 40 г/моль, водорода 2 г/моль.
13.52. Одинаковые массы водорода и гелия поместили в сосуд объема V1, который отделен от откачанного до состояния вакуума сосуда объема V2 полунепроницаемой перегородкой, пропускающей только молекулы водорода. После установления равновесия давление в первом сосуде упало в два раза. Температура постоянна. Определите отношение V2/V1.
13.53. сосуд заполнен смесью водорода и гелия и отделен от равного ему по объему откачанного сосуда неподвижной полупроницаемой перегородкой, пропускающей только атомы гелия. После установления равновесия давление в первом сосуде упало на 10 % . Температура постоянна. Определите отношение массы гелия к массе водорода.
13.54. Закрытый сосуд разделен на две одинаковые по объему части твердой неподвижной полупроницаемой перегородкой. В первую половину сосуда введена смесь аргона и водорода при давлении p = 1,5 × 105 Па, во второй половине вакуум. Через перегородку может диффундировать только водород. После окончания процесса диффузии давление в первой половине сосуда оказалось равным 1,0 × 105 Па. Во время процесса температура системы оставалась постоянной. Определите отношение масс аргона и водорода в смеси, которая была первоначально введена в первую половину сосуда. Молярная масса аргона 40 г/моль, водорода 2 г/моль.
13.55. Две сферы с объемами 100 см3 и 200 см3 соединены короткой трубкой, в которой имеется пористая перегородка. С ее помощью можно добиться в сосудах равенства давления, но не температуры. Сначала система находится при температуре To = 300 K и содержит кислород под давлением po = 1,0 × 105 Па. Затем малую сферу помещают в сосуд со льдом при температуре t1 = 0 °С, а большую в сосуд с паром при температуре t2 = 100 °C. Какое давление p установится в системе? Тепловым расширением сфер пренебречь.
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Три одинаковых сосуда, содержащих разреженный газ, соединены друг с другом трубками малого диаметра: первый сосуд — со вторым, второй — с третьим. Первоначально давление газа в сосудах было равно соответственно (р, 3р) и (р). В ходе опыта сначала открыли и закрыли кран, соединяющий второй и третий сосуды, а затем открыли и закрыли кран, соединяющий первый сосуд со вторым. Как изменилось в итоге (уменьшилось, увеличилось или осталось неизменным) количество газа в первом сосуде? (Температура газа оставалась в течение всего опыта неизменной.)
1) При первой открывании и закрывании кранов, в соответствии законам Дальтона и Бойля-Мариотта, установившееся давление во втором и третьем сосудах будет [dfrac{3p}{2}+dfrac{p}{2}=2p] 2) При втором открывании и закрывании, с учетом тех же законов, установившееся давление в первом и втором будет равно [dfrac{2p}{2}+dfrac{p}{2}=1,5p] 3) Так как объем сосуда не изменился, а температура по условию постоянна, то в соответствии закону Клайперона – Менделеева [pV=nu R T Rightarrow nu=dfrac{pV}{RT}] Знаменатель остался прежним, а числитель увеличился, значит и количество газа увеличилось.
Ответ:
Сжиженные газы с низкими температурами кипения хранят в открытых теплоизолированных резервуарах при нормальном давлении, с контактом с атмосферой. При таком хранении потери на испарение, отнесённые к единице массы сжиженного газа, уменьшаются при увеличении объёма сосуда. Объясните причины вышеизложенного, основываясь на известных физических законах и закономерностях.
1) Даже при хорошей теплоизоляции невозможно устранить полностью подвод тепла к сжиженным газам, значит, будет некоторое испарение вещества, потому что температура кипения таких газов ниже температуры атмосферы и существует теплопроводность.
2) Так как существует испарение, то в закрытых сосудах будет повышаться давление, что приведет к взрыву, поэтому газ хранят в открытых сосудах.
3) Подвод тепла к газу через стенки сосуда пропорционален площади стенок сосуда, а его масса пропорциональна объему. Объем же в свою очередь пропорционален кубу размеров сосуда. Поэтому с увеличением объема уменьшается испарение на единицу массы.
Ответ:
Чтобы вода в резервуаре быстрее закипела, источник тепла всегда помещают внизу. Желая охладить кастрюлю с горячей водой как можно быстрее, кастрюлю поставили на лёд. Является ли такой способ эффективным? Ответ поясните, указав какие физические явления и закономерности вы использовали для объяснения.
Нет, неверно.
Нагреватель ставится внизу, потому что нагретые слои воды, как более легкие, поднимаются вверх и таким образом достигается наиболее эффективное перемешивание и нагревание всей воды (по такому же принципу работает батарея в комнате). При охлаждении же дело происходит как раз наоборот: более холодные слои воды, как более тяжелые, опускаются вниз. Поэтому если поместить холодильник внизу, то перемешивания не будет, и остывание будет идти очень долго. Для более быстрого охлаждения надо поместить лед сверху.
Ответ:
На рисунке изображены графики двух процессов, проведённых с идеальным газом при одном и том же давлении. Графики процессов представлены на рисунке. Почему изобара (I) лежит выше изобары (II)? Ответ поясните, указав, какие физические закономерности Вы использовали для объяснения. 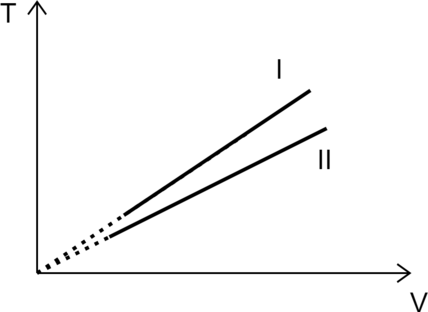
1. Идеальный газ подчиняется закону Клапейрона–Менделеева: [pV=nu R T,] где (p) – давление газа, (V) – объем, (nu) – количество газа, (T) – температура газа в Кельвинах.
Выразим температуру [T=dfrac{pV}{nu R}] 2. Зафиксируем объем (V_0), при этом отношение температур равно [dfrac{T_I}{T_{II}}=dfrac{dfrac{pV_0}{nu_I R}}{dfrac{pV_0}{nu{II}R}}=dfrac{nu_{II}}{nu_{I}}>1] Значит количество газа во втором больше, чем количество газа в первом.
Ответ:
1 моль разреженного гелия участвует в циклическом процессе 1–2–3–4–1, график которого изображён на рисунке в координатах V–T, где V — объём газа, Т — абсолютная температура. Постройте график цикла в координатах p–V, где р — давление газа, V— объём газа. Опираясь на законы молекулярной физики и термодинамики, объясните построение графика. Определите, во сколько раз работа газа в процессе 2–3 больше модуля работы внешних сил в процессе 4–1. 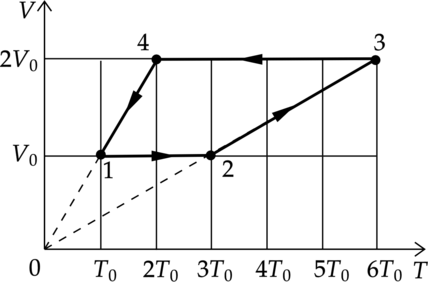
Проанализируем процессы:
1–2: Процесс изохорный, по закону Шарля (dfrac{p}{T}=const), температура увеличилась в 3 раза, значит и давление увеличилось в 3 раза.
2–3: Процесс изобарный, по закону Гей–Люсака (dfrac{V}{T}=const) и объем и температура увеличились в 2 раза.
3–4: В процессе 3–4 газ изохорно уменьшил свою абсолютную температуру и давление в 3 раза.
4–1: Газ вернулся в первоначальное состояние Перестроим график цикла в координатах p–V (см. рисунок). 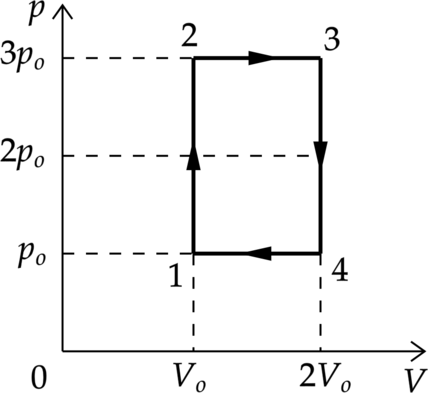
Работа газа в процессе 2–3 равна [A_{23}=pDelta V=3p_(2V_0-V_0)=3p_0V_0] Работа внешних сил в процессе 4–1 равна [|A_{41}|=pDelta V=p_0(2V_0-V_0)=p_0V_0] Значит работа газа в процессе 2–3 в 3 раза больше работы внешних сил в процессе 4–1.
Ответ:
На рисунке 1 приведена зависимость внутренней энергии (U) 2 моль идеального одноатомного газа от его давления p в процессе 1–2–3. Постройте график этого процесса на рисунке 2 в переменных (p—V). Точка, соответствующая состоянию 1, уже отмечена на этом рисунке. Построение объясните, опираясь на законы молекулярной физики. 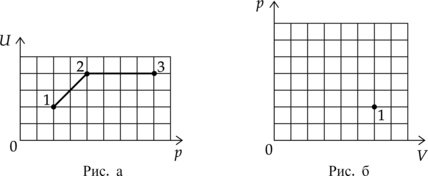
1. Проанализируем процессы:
1–2: Внутренняя энергия прямо пропорциональна температуре газа (U=dfrac{3}{2}nu R T ), значит в процессе 1–2 температура увеличивается, давление тоже увеличивается (по графику ). По основному газовому закону (dfrac{pV}{T}=const) объем будет постоянен. График будет представлять собой вертикальную прямую
2–3: В процессе 2–3 внутренняя энергия газа постоянна, а значит и температура постоянна (по пункту 1), давление увеличивается, значит, по основному газовому закону объем будет уменьшаться. График будет представлять гиперболу.
2. Построим график

Ответ:
На графике представлена зависимость давления неизменной массы идеального газа от его плотности. Опишите, как изменяются в зависимости от плотности температура и объём газа в процессах 1–2 и 2–3. 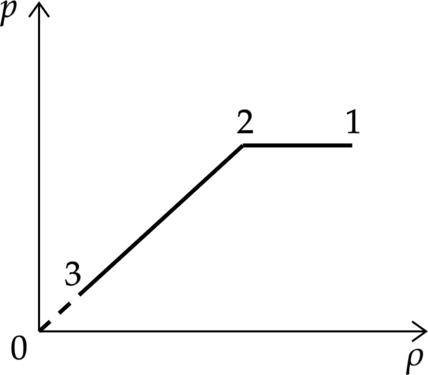
1. Плотность находится по формуле: [rho=dfrac{m}{V} quad (1)] тогда уравнение Клайперона–Менделеева можно переписать в виде [pV=dfrac{m}{mu}RT Rightarrow p=dfrac{rho}{mu}RT, quad (2)] где (m) – масса газа, (V) – его объем, (T) – температура газа. 2. Процесс 1–2.
Плотность уменьшается при постоянном, в соответствии с формулой (1) объем будет увеличиваться, а температура будет увеличиваться в соответствии с формулой (2).
Процесс 2–3.
Плотность уменьшается вместе с давлением, причем давление уменьшается пропорционально плотности (p sim rho), а это означает, что температура газа постоянна, а по формуле (1) объем увеличивается.
Ответ:
Источник
Автор
Тема: Два одинаковых сосуда наполнены идеальным газом и соединены краном (Прочитано 13089 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Два одинаковых сосуда наполнены идеальным газом и соединены краном. В первом сосуде средняя квадратичная скорость молекул равна U1, а во втором U2. По какой формуле можно определить среднюю квадратичную скорость молекул после открытия крана, если число молекул газа в первом сосуде в n раз больше, чем во втором.
Капельян Физика пособие для подготовки к ЦТ Обобщающий тест №9 задача №2 с.322
Моё рещение:
1) Расписываю давление каждого газа через основное уравнение МКТ.
2) Записываю закон Дальтона
P0=P1 + P2
3) После подстановки в последюю формулу первых трёх и сокращения получаю ответ, отличающийся в корень из двух от того, что в книге.
Думаю ошибка в законе Дальтона.
После открытия крана давление в сосудах изменится и будет равно P’1 и P’2 .
Прав ли я?
P0=P’1 + P’2
Я не знаю как найти эти штриховые давления.
Нужна, подсказка.
Подсказка оплачена 06.01. ( Нарушаю правила, простите)
« Последнее редактирование: 06 Января 2013, 19:55 от pml »
Записан
1. Обозначайте скорость этой буквой: υ (буквой V обозначается объем).
2. Давление поменяется, и найти можно через уравнение Клапейрона (объем увеличивается в два раза). Но в условии ничего не говорится про температуру (а это важно для решения). Поэтому или считайте, что температура не меняется, или есть какой-то другой способ, но я его пока не вижу.
Записан
Среднеквадратичная скорость меняется, значит, меняется температура.
Полный тупик.
Надо бы Семёна Наумовича Капельяна побеспокоить.
Записан
Среднеквадратичная скорость меняется, значит, меняется температура.
Вы правы, здесь я ошибся. Выразите температуру через квадратичную скорость и решите систему уравнений.
Записан
Решил, получил тождество 0=0.
Если у вас решается, то готов оплатить решение.
« Последнее редактирование: 06 Января 2013, 21:28 от pml »
Записан
Воспользуемся законом сохранения энергии кинетической энергии молекул газа (по условию газ идеальный, поэтому потенциальной энергии нет):
Wk0 = Wk1 + Wk2,
где Wk0 — кинетическая энергия молекул смеси газов (N1 + N2 — молекул)), Wk1, Wk2 — кинетические энергии молекул газов в первом сосуде и во втором. Тогда с учетом того, что в сосудах один и тот же газ, и N1 = n∙N2 (т.к. число молекул газа в первом сосуде в n раз больше, чем во втором), получаем:
[begin{array}{c} {left(N_{1} +N_{2} right)cdot frac{m_{0} cdot leftlangle upsilon _{3}^{2} rightrangle }{2} =N_{1} cdot frac{m_{0} cdot leftlangle upsilon _{1}^{2} rightrangle }{2} +N_{2} cdot frac{m_{0} cdot leftlangle upsilon _{2}^{2} rightrangle }{2} ,} \ {left(N_{1} +N_{2} right)cdot leftlangle upsilon _{3}^{2} rightrangle =N_{1} cdot leftlangle upsilon _{1}^{2} rightrangle +N_{2} cdot leftlangle upsilon _{2}^{2} rightrangle ,} \ {left(ncdot N_{2} +N_{2} right)cdot leftlangle upsilon _{3}^{2} rightrangle =ncdot N_{2} cdot leftlangle upsilon _{1}^{2} rightrangle +N_{2} cdot leftlangle upsilon _{2}^{2} rightrangle ,; ; ; left(n+1right)cdot leftlangle upsilon _{3}^{2} rightrangle =ncdot leftlangle upsilon _{1}^{2} rightrangle +leftlangle upsilon _{2}^{2} rightrangle ,} \ {leftlangle upsilon _{3}^{2} rightrangle =frac{ncdot leftlangle upsilon _{1}^{2} rightrangle +leftlangle upsilon _{2}^{2} rightrangle }{n+1} ,; ; ; leftlangle upsilon _{3} rightrangle =sqrt{frac{ncdot leftlangle upsilon _{1}^{2} rightrangle +leftlangle upsilon _{2}^{2} rightrangle }{n+1} } .} end{array}]
Через давление задачу решить не получилось.
« Последнее редактирование: 29 Октября 2013, 12:48 от alsak »
Записан
Источник
