Два сосуда наполнены одним и тем же
Среднее число столкновений и средняя длина свободного пробега молекул Молекулы
газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг
с другом. Между двумя последовательными столкновениями молекулы проходят некоторый
путь l, который называется длиной свободного пробега. В общем случае длина пути
между последовательными столкновениями различна, но так как мы имеем дело с огромным
числом молекул и они находятся в беспорядочном движении, то можно говорить о средней
длине свободного пробега молекул
Два сосуда наполнены одним и тем же газом под давлением 4×105
Па и 9×105 Па массой 0,2 кг
и 0,3 кг соответственно. Сосуды соединяют трубкой, объемом которой можно пренебречь
по сравнению с объемами сосудов. Найдите установившееся давление в сосудах,
если температура газа в них была одинакова и после установления равновесия
увеличилась на 20%. Ответ представьте в атмосферах (1 атм = 105 Па) и округлите
до десятых.
Дано: p1 = 4×105 p2 = 9×105 m1 = 0,2 кг m2 = 0,3 кг T¢ = 1,2 T 1 атм = 105 Па | Решение: |
установившееся давление в сосудах можно определить из закона Дальтона: р = р¢1 + р¢2, (1) где р¢1, р¢2 – парциальные давления газа. Эти давления p¢(V1 + V2) = RT¢ Þ p¢ = RT¢, | |
p = ? |
где Т¢ – температура
газа после соединения сосудов трубкой,
p¢ – парциальное давление,
т.е. давление, которое создается газом, если бы он один занимал весь объем.
Подставим выражение (2) в закон дальтона(1):
р¢ = RT¢+ RT¢. (3)
Учитывая условие задачи, согласно которому
T¢ = 1,2 T,
уравнение (3) примет вид:
р = 1,2R T + 1,2R T = 1,2(m1 + m2). (4)
Объемы V1, V2 выразим также из уравнения Клапейрона – Менделеева, которое
записано для случая, когда сосуды еще не соединены трубкой.
V = RT (5)
Полученное выражение для объема подставим в уравнение(5).
р = 1,2×(m1 + m2) = 1,2×(m1 + m2) =
= 1,2× (m1 + m2) =1,2×.
Подставим численные значения и рассчитаем установившееся давление.
р =1,2× = 7,2×105 (Па) = 7,2 (атм).
Ответ: р = 7,2 атм
До сих поp все pассуждения были пpоведены относительно
одной ИСО К. Введем тепеpь движущуюся систему отсчета К’ : допустим, что pакета
3 со скоpостью v движется от пеpвой pакеты ко втоpой. На pис. 5.2 ось ct’ изобpажает
pазвеpтку событий во вpемени, пpоходящих на pакете 3. Ось Ох, согласно опpеделению
Эйнштейна, изобpажает совокупность событий, одновpеменных с событием “О”.
Какое событие на pакете 3 следует считать одновpеменным с событием “О”?
Такой же вопpос мы сначала ставили относительно pакеты 2. По существу, он нами
уже pешен: событие, пpоисходящее на pакете 3 и одновpеменно с “О”, pасположено
на пеpесечении пpямых Ох и сt’, т.е. изобpажается точкой е’ . Однако будем пpидеpживаться
точки зpения наблюдателя, находящегося на pакете 3. Пpимем за неподвижную ИСО
К’ – пpинцип относительности допускает такой подход. Пpомежуток a’ b’ изобpажает
совокупность абсолютно отоpванных от “О” событий, пpоисходящих на pакете
3. Точка е’ не лежит посеpедине этого пpомежутка. Свет от pакеты 3 до pакеты 1
доходит за вpемя t1’= b’ е’ /c , обpатно он доходит за вpемя t2′ = e’a’/c.
Из pис. 5.2 видно, что t2′ > t1′.
Конечно, так и должно быть, т.к. на пpямом пути свет пpоходит меньший отpезок,
чем на обpатном – за вpемя движения сигнала pакета 3 удаляется от pакеты 1. Однако
с точки зpения наблюдателя, связанного с системой 3, эта ноpмальная ситуация означает,
что скоpость света неизотpопна : пpотив оси х свет pаспpостpаняется быстpее, чем
вдоль этой оси. Наблюдатель на pакете 3 (в системе К’ ), пользуясь неоднозначностью
понятия одновpеменности, имеет основание пеpефоpмулиpовать выбоp одновpеменных
событий и пpивести его в соответствие с опpеделением Эйнштейна. Для этого он пpимет
за одновpеменные с “О” события, лежащие на оси х , пpоходящей чеpез
сеpедину отpезка a’ b’. Условимся так поступать во всех случаях, когда обpащаемся
к какой – то новой ИСО.
Тогда понятие одновpеменности станет относительным
: в каждой ИСО
по своему осуществляется выбоp одновpеменных событий, хотя
пpинцип выбоpа во всех ИСО будет один и тот же. События, одновpеменные в одной
системе отсчета, будут неодновpеменными в дpугой системе отсчета. Подчеpкнем,
что одновpеменность становится относительной благодаpя неоднозначности этого понятия.
Броуновское движение. Шотландский ботаник Р. Броун (1773—1858),
наблюдая под микроскопом взвесь цветочной пыльцы в воде, обнаружил, что частицы
пыльцы оживленно и беспорядочно двигались, то вращаясь, то перемещаясь с места
на место, подобно пылинкам в солнечном луче. Впоследствии оказалось, что подобное
сложное зигзагообразное движение характерно для любых частиц малых размеров (»1
мкм), взвешенных в газе или жидкости. Интенсивность этого движения, называемого
броуновским, повышается с ростом температуры среды, с уменьшением вязкости и размеров
частиц (независимо от их химической природы). Причина броуновского движения долго
оставалась неясной.
Источник
Физика, Помогите плз! |
15.02.2006 – 18:28 Сообщение | |
Наглый похуист Сообщений: 2910 | Такая проблема в общем, на завтра надо сделать задачу по физике, я уже часа два сижу, вообще не понимаю че делать, хреново у меня с физикой Если кто то шарит по физике – помогите плз ——————– |
15.02.2006 – 18:56 Сообщение | |
Lore of Nén Сообщений: 4212 | 7,2 атм ур-е состояния газа для 1го сосуда: то же для 2го сосуда: и для соединенных трубкой сосудов в равновесном состоянии: Px*(V1+V2)=(m1+m2)*R*T2/M, (3) причём T2=1,2T по усл. делим 1е на 2е, получаем отношение объемов V1:V2= 3:2, Сообщение отредактировал pmn – 15.02.2006 – 19:09 ——————– ++++++++++[>+++++++>++++++++++>+++>+<<<<-]>++ .>+.+++++++..+++.>++.<<+++++++++++++++.>.+++. ——.——–.>+.>. |
15.02.2006 – 18:58 Сообщение | |
o_O Сообщений: 2228 | прошло прошло Сообщение отредактировал коФка – 15.02.2006 – 18:58 |
15.02.2006 – 19:07 Сообщение | |
Наглый похуист Сообщений: 2910 | тока мне с решением надо ——————– |
15.02.2006 – 19:08 Сообщение | |
Lore of Nén Сообщений: 4212 | 2коФка: если типа прикол такой, типа поиздеваться, то я щас тоже дам задачу тоже типа из школьной программы Сообщение отредактировал pmn – 15.02.2006 – 19:08 ——————– ++++++++++[>+++++++>++++++++++>+++>+<<<<-]>++ .>+.+++++++..+++.>++.<<+++++++++++++++.>.+++. ——.——–.>+.>. |
15.02.2006 – 19:10 Сообщение | |
Наглый похуист Сообщений: 2910 | 2pmn: Мегасенкс и мегареспект щас буду пытатся въехать ——————– |
15.02.2006 – 19:13 Сообщение | |
Lore of Nén Сообщений: 4212 | за правильность ответа не отвечаю ——————– ++++++++++[>+++++++>++++++++++>+++>+<<<<-]>++ .>+.+++++++..+++.>++.<<+++++++++++++++.>.+++. ——.——–.>+.>. |
15.02.2006 – 19:13 Сообщение | |
o_O Сообщений: 2228 | |
15.02.2006 – 19:14 Сообщение | |
Наглый похуист Сообщений: 2910 | 2pmn: точно, главное что нибудь написать =) ——————– |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей:
Источник
Два сосуда наполнены одним и тем же газом под давлением 4×105
Па и 9×105 Па массой 0,2 кг
и 0,3 кг соответственно. Сосуды соединяют трубкой, объемом которой можно пренебречь
по сравнению с объемами сосудов. Найдите установившееся давление в сосудах,
если температура газа в них была одинакова и после установления равновесия
увеличилась на 20%. Ответ представьте в атмосферах (1 атм = 105 Па) и округлите
до десятых.
Дано: p1 = 4×105 p2 = 9×105 m1 = 0,2 кг m2 = 0,3 кг T¢ = 1,2 T 1 атм = 105 Па | Решение: |
установившееся давление в сосудах можно определить из закона Дальтона: р = р¢1 + р¢2, (1) где р¢1, р¢2 – парциальные давления газа. Эти давления p¢(V1 + V2) = RT¢ Þ p¢ = RT¢, | |
p = ? |
где Т¢ – температура
газа после соединения сосудов трубкой,
p¢ – парциальное давление,
т.е. давление, которое создается газом, если бы он один занимал весь объем.
Подставим выражение (2) в закон дальтона(1):
р¢ = RT¢+ RT¢. (3)
Учитывая условие задачи, согласно которому
T¢ = 1,2 T,
уравнение (3) примет вид:
р = 1,2R T + 1,2R T = 1,2(m1 + m2). (4)
Объемы V1, V2 выразим также из уравнения Клапейрона – Менделеева, которое
записано для случая, когда сосуды еще не соединены трубкой.
V = RT (5)
Полученное выражение для объема подставим в уравнение(5).
р = 1,2×(m1 + m2) = 1,2×(m1 + m2) =
= 1,2× (m1 + m2) =1,2×.
Подставим численные значения и рассчитаем установившееся давление.
р =1,2× = 7,2×105 (Па) = 7,2 (атм).
Ответ: р = 7,2 атм
До сих поp все pассуждения были пpоведены относительно
одной ИСО К. Введем тепеpь движущуюся систему отсчета К’ : допустим, что pакета
3 со скоpостью v движется от пеpвой pакеты ко втоpой. На pис. 5.2 ось ct’ изобpажает
pазвеpтку событий во вpемени, пpоходящих на pакете 3. Ось Ох, согласно опpеделению
Эйнштейна, изобpажает совокупность событий, одновpеменных с событием “О”.
Какое событие на pакете 3 следует считать одновpеменным с событием “О”?
Такой же вопpос мы сначала ставили относительно pакеты 2. По существу, он нами
уже pешен: событие, пpоисходящее на pакете 3 и одновpеменно с “О”, pасположено
на пеpесечении пpямых Ох и сt’, т.е. изобpажается точкой е’ . Однако будем пpидеpживаться
точки зpения наблюдателя, находящегося на pакете 3. Пpимем за неподвижную ИСО
К’ – пpинцип относительности допускает такой подход. Пpомежуток a’ b’ изобpажает
совокупность абсолютно отоpванных от “О” событий, пpоисходящих на pакете
3. Точка е’ не лежит посеpедине этого пpомежутка. Свет от pакеты 3 до pакеты 1
доходит за вpемя t1’= b’ е’ /c , обpатно он доходит за вpемя t2′ = e’a’/c.
Из pис. 5.2 видно, что t2′ > t1′.
Конечно, так и должно быть, т.к. на пpямом пути свет пpоходит меньший отpезок,
чем на обpатном – за вpемя движения сигнала pакета 3 удаляется от pакеты 1. Однако
с точки зpения наблюдателя, связанного с системой 3, эта ноpмальная ситуация означает,
что скоpость света неизотpопна : пpотив оси х свет pаспpостpаняется быстpее, чем
вдоль этой оси. Наблюдатель на pакете 3 (в системе К’ ), пользуясь неоднозначностью
понятия одновpеменности, имеет основание пеpефоpмулиpовать выбоp одновpеменных
событий и пpивести его в соответствие с опpеделением Эйнштейна. Для этого он пpимет
за одновpеменные с “О” события, лежащие на оси х , пpоходящей чеpез
сеpедину отpезка a’ b’. Условимся так поступать во всех случаях, когда обpащаемся
к какой – то новой ИСО.
Тогда понятие одновpеменности станет относительным
: в каждой ИСО
по своему осуществляется выбоp одновpеменных событий, хотя
пpинцип выбоpа во всех ИСО будет один и тот же. События, одновpеменные в одной
системе отсчета, будут неодновpеменными в дpугой системе отсчета. Подчеpкнем,
что одновpеменность становится относительной благодаpя неоднозначности этого понятия.
Обсуждая до сих пор силы, мы не интересовались их происхождением. Однако в механике
мы будем рассматривать различные силы: трения, упругости, тяготения. Из опыта
известно, что всякое тело, движущееся по горизонтальной поверхности другого тела,
при отсутствии действия на него других сил с течением времени замедляет свое движение
и в конце концов останавливается. Это можно объяснить существованием силы трения,
которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы
трения зависят от относительных скоростей тел. Силы трения могут быть разной природы,
но в результате их действия механическая энергия всегда превращается во внутреннюю
энергию соприкасающихся тел.
Источник
2017-10-13 ![]()
Два сосуда объемом $V = 10 л$ каждый наполнены сухим воздухом при давлении $V = 1 атм$ и температуре $t_{0} = 0^{ circ} С$. В первый вводят $m_{1} = 3 г$ воды, во второй $m_{2} = 15 г$ и нагревают сосуды до температуры $t = 100^{ circ} С$. Определить давление влажного воздуха при этой температуре в каждом сосуде.
Решение:
Введенная в сосуд вода испаряется, и давление в сосуде согласно закону Дальтона становится равным сумме парциальных давлений воздуха и паров воды.
Парциальное давление воздуха $p$ в обоих сосудах одинаково и легко находится с помощью закона Шарля, так как нагревание неизменной массы воздуха происходит при постоянном объеме (ибо тепловым расширением сосуда можно пренебречь):
$p = p_{0} T/T_{0} = 1 атм cdot 373 К/273 К= 1,37 атм$.
Теперь определим парциальное давление $p_{1}$ водяного пара в первом сосуде при $100^{ circ} С$. Для этого воспользуемся уравнением Менделеева — Клапейрона
$p_{1} = frac{1}{V} frac{m_{1}}{ mu} RT$. (1)
Подставляя в (1) числовые значения всех величин ($R = 0,082 атм cdot л/(моль cdot ^{ circ}С), mu = 0,018 кг/моль$), находим $p_{1} = 0,51 атм
Подсчитав таким же образом парциальное давление водяного пара во втором сосуде, получим $p_{2} = 2,55 атм > 1 атм$.
Итак, казалось бы, полное давление во втором сосуде
$p + p_{2} = 3,92 атм$.
Но не будем торопиться. Подумаем, может ли давление водяного пара при $100^{ circ} С$ быть больше 1 атм. Вспомним, что при давлении 1 атм вода кипит при $100^{ circ} С$. Это значит, что давление насыщенного водяного пара равно 1 атм при $100^{ circ} С$. Другими словами, давление водяного пара при $100^{ circ} С$ при наличии свободной поверхности жидкости никогда не может превышать 1 атм. Поэтому во втором сосуде вода испарилась не полностью, пар будет насыщенным и его парциальное давление равно 1 атм. Полное давление в этом сосуде $ p + 1 атм = 2,37 атм$.
Подумайте теперь, как можно подсчитать массу неиспарившейся воды во втором сосуде.
При решении этой задачи для нахождения давления водяного пара мы использовали закон Менделеева — Клапейрона — уравнение состояния идеального газа. Это можно делать для достаточно разреженного пара независимо от того, является ли он насыщенным или нет. Однако содержание закона в этих двух случаях совершенно различно. Если пар далек от насыщения, то, используя уравнение (1), мы находим давление пара, которое оказывается весьма близким к наблюдаемому на опыте. Для насыщенного пара использование этого уравнения для нахождения давления приводит, как мы только что видели, к абсурду. Однако это не означает, что закон неверен. Если вычисленное по уравнению (1) давление водяного пара оказывается больше, чем давление насыщенного пара при данной температуре, то это означает, что на самом деле масса пара меньше той, которую мы подставляли в уравнение,— часть вещества находится в жидкой фазе. Подставляя в формулу (1) давление насыщенного пара, взятое из таблиц, можно из нее найти массу насыщенного пара, содержащегося в объеме $V$ при температуре $T$.
Таким образом, применяя уравнение Менделеева — Клапейрона к парам, нужно все время иметь под рукой таблицу зависимости давления насыщенного пара от температуры, т. е. зависимости температуры кипения от давления.
Теперь вы без труда сможете ответить на поставленный дополнительный вопрос — определить массу неиспарившейся воды во втором сосуде.
Источник

P | m | RT RT. | |||||||
V | |||||||||
Если | рассматривать | смесь | газов, | ||||||
заполняющих объём V при температуре Т, тогда, | |||||||||
парциальные | давления, | можно найти, | как: | ||||||
P m1RT | , | P m2 RT , ….. | P mn RT | ||||||
1 | 1V | 2 | 2V | n | nV | ||||
31

Согласно закону Дальтона: полное давление смеси газа равно сумме парциальных давлений всех газов, входящих в смесь
P = P1 + P2 + … + Pn
Отсюда, с учетом вышеизложенного, можно
записать | m2 | mn | |||
m1 | … | RT | |||
PV | |||||
1 | 2 | ||||
n | |||||
– это уравнение Менделеева-Клапейрона для
смеси газов.
32

33
Пример1.
Баллон содержит газ при 27°С и давлении 200 кПа. Каково будет давление (в кПа), если из баллона выпустить 80% газа и охладить его до 12°С?
Дано: t1 = 27°С, Т1 = 300К; р1= 200 кПа = 2 105Па; t2 = 12°С, Т1=285К; =0,8; m2 = 0,2m1.
Найти: р2.

34
Так как масса газа в баллоне меняется, то начальное и конечное состояния газа в баллоне нельзя связывать объединенным газовым законом (или уравнением изохорного процесса). Нужно для каждого состояния
записать | уравнение | Клапейрона-Менделеева | |||||
p1V | m1 | , | p2V | m2 | |||
M | M | ||||||
и, поделив эти уравнения друг на друга, найти конечное | |||||||
давление | |||||||
и, поделив эти уравнения друг на друга, найти конечное давление

35
p1V | M | |||||
m1RT1 | , | |||||
p2V | ||||||
M | 0,2m1RT2 | |||||
p1 | ||||||
T1 | , | |||||
p2 | ||||||
0,2T2 | ||||||
p2 0,2 p1 T2 , T1
p2 0,2 2 105 300285 38 103 Па 38 кПа .
Ответ: p2 = 38 кПа

36
Пример 2.
Определите минимальный объем наполненного водородом шара, который может поднять человека массой 70 кг на высоту 100 м за время 30 с. Общая масса оболочки шара и корзины 20 кг. Принять g = 10 м с2, плотность воздуха и водорода соответственно равными 1,3 кг м3 и 0,1 кг м3. Сопротивлением воздуха пренебречь. Ответ представьте в единицах СИ и округлите до целого числа.
Дано: 0 = 0, m1 = 70 кг, h = 100 м, t = 30 с, m2 = 20 кг, g = 10 м с2, возд = 1,3 кг м3, вод = 0,1 кг м3
Найти:
Vmin.

37
mчa mш a mH a FA mч g mш g mH g
Полученное выражение запишем в проекции на ось y:
mчa + mшa + mНa = FA – mчg – mшg – mНg.

38
(mч + mш)a + mНa = вgV – (mч + mш)g – mНg.
(mч + mш)a + НVa = вgV – (mч + mш)g – НVg.
НVa – вgV + НVg = – (mч + mш)a – (mч + mш)g.
V( вg – Нa – Нg) = (mч + mш)a + (mч + mш)g.
V( вg – Нa – Нg) = (mч + mш)(a + g).
(mч mш )(a g) V = g(ρв ρН ) ρН a .
В полученном выражении остается неизвестным ускорение, с которым шар поднимается вверх. Найти ускорение можно из уравнения движения шара.

39
h 0t | at2 | at | 2 | . | ||||||||||||||
2 | 2 | |||||||||||||||||
Тогда ускорение шара | 2h | |||||||||||||||||
a t2 . | ||||||||||||||||||
(m m )( | 2h | g) | ||||||||||||||||
Vmin | ч | ш | t2 | |||||||||||||||
g(ρ | в | ρ | Н | ) ρ | Н | 2h | ||||||||||||
t2 | ||||||||||||||||||
2 100 | . | |||||||||||||||||
90 ( | 10) | |||||||||||||||||
900 | 3 | |||||||||||||||||
Vmin | 77 (м | ) | ||||||||||||||||
2 100 | ||||||||||||||||||
10(1,3 0,1) 0,1 | 900 | |||||||||||||||||
Ответ: Vmin = 77м3

40
Пример 3.
Два сосуда наполнены одним и тем же газом под давлением 4 105 Па и 9 105 Па массой 0,2 кг и 0,3 кг соответственно. Сосуды соединяют трубкой, объемом которой можно пренебречь по сравнению с объемами сосудов. Найдите установившееся давление в сосудах, если температура газа в них была одинакова и после установления равновесия увеличилась на 20%. Ответ представьте в атмосферах (1 атм = 105 Па) и округлите до десятых.
Дано: p1 = 4 105 Па, p2 = 9 105 Па, m1 = 0,2 кг, m2 = 0,3 кг, T = 1,2 T, 1 атм = 105 Па
Найти: p.

41
Установившееся давление в сосудах можно определить из закона Дальтона:
р = р 1 + р 2, где р 1, р 2 – парциальные давления газа. Эти давления
определяем из уравнения Клапейрона – Менделеева: p (V1 V2) Mm RT
p mRT , M V1 V2
где Т – температура газа после соединения сосудов трубкой, p – парциальное давление, т.е. давление, которое создается газом, если бы он один занимал весь объем.

42
Подставим выражение в закон Дальтона:
m1RT | m2 RT | |
p | . | |
M V1 V2 | M V1 V2 | |
Учитывая условие задачи, согласно которому T = 1,2 T,
уравнение для давления примет вид:
p | 1,2m1RT | 1,2m2 RT | 1,2RT | (m1 m2). | ||
M V1 V2 | M V1 V2 | M V1 V2 |
Объемы V1, V2 выразим также из уравнения Клапейрона –
Менделеева, которое записано для случая, когда сосуды еще не соединены трубкой.

43
V mRTpM ,
Тогда
p | 1,2RT | (m m ) | 1,2RT(m1 | m2) | 1,2(m1 m2) . | |||||||||
M V1 V2 | m RT | |||||||||||||
1 | 2 | m RT | m1 | m2 | ||||||||||
M | 1 | 2 | p1 | p2 | ||||||||||
p M | p | M | ||||||||||||
1 | 2 | |||||||||||||
p | 1,2(0,2 0,3) | 7,2 105 | Па 7,2 атм . | |||||||||||
0,2 | 0,3 | |||||||||||||
4 | 105 | 9 105 | ||||||||||||
Ответ: р = 7,2 атм

44
Пример 4. Идеальный одноатомный газ массой 1 кг с молярной массой 4 г/моль нагревают так, что его температура, пропорциональная квадрату давления, возрастает от 300 К до
600 К. | Определите | работу, | совершенную | газом. |
Универсальная газовая постоянная | 8,31 Дж/(моль К). Ответ | |||
представьте в килоджоулях и округлите до целого числа.
Дано: m = 1 кг, M = 4 г/моль = 4 10-3 кг/моль, Т = k p2, T1 = 300 К, T2 = 600 К, R = 8,31 Дж/(моль К), i = 3.
Найти: А.

45
Работу, совершенную газом удобнее найти графически. Известно геометрический смысл работы. Она представляет собой площадь фигуры под графиком в pV – координатах. Для этого нужно построить этот график, то есть определить зависимость p = f(V). Для этого запишем уравнение Клапейрона – Менделеева:
pV = RT.
По условию задачи
Т = k p2,
следовательно,
где , R и k – постоянные величины, т.е. V p. Тогда график зависимости p = f(V) будет выглядеть следующим образом:

46
При t 0, т.е. на бесконечно малом участке траектории перемещение совпадает с траекторией ( s = r).
В этом случае мгновенную скорость можно выразить через
Фигура между графиком и осью х представляет собой трапецию. Значит, работа численно равна площади трапеции.
Sтрап a 2 b h,

47
то есть | А | p1 p2 | (V V ), | ||||||||||||||||||||||
2 | 2 | 1 | |||||||||||||||||||||||
где | |||||||||||||||||||||||||
T | |||||||||||||||||||||||||
T | |||||||||||||||||||||||||
p | k , | V Rkp | Rk | k . | |||||||||||||||||||||
T1 | T2 | νRk | |||||||||||||||||||||||
(νRk T2 | T1 ) | ( T2 | T1 | ||||||||||||||||||||||
A | k | k | νRk | ) | |||||||||||||||||||||
2 | |||||||||||||||||||||||||
k | k | 2 | k | k | |||||||||||||||||||||
mR | (T2 | T1) | 1 8,31 | (600 300) 312 кДж . | |||||||||||||||||||||
2M | 2 4 10 3 | ||||||||||||||||||||||||
Ответ: А = 312 кДж

48
Пример 5.
По газопроводной трубе идет углекислый газ CO2 под
давлением 3,92 105 Па при температуре 280 К. Какова средняя скорость движения газа в трубе, если через поперечное сечение трубы, равное 5 см2, за время 10 мин протекает газ массой 20 кг? Универсальная газовая постоянная 8,31 Дж/(моль К), молярная масса углекислого газа 44 г/моль. Ответ представьте в единицах СИ и округлите до целого числа.
Дано: CO2, p = 3,92 105 Па, T = 280 К, s = 5 см2 = 5 10-4 м2, t = 10 мин = 600 c, m = 20 кг, R = 8,31 Дж/(моль К),
M = 44 г/моль = 44 10-3кг/ моль
Найти: ср.

49
Средняя скорость – это весь путь нужно разделить на все
время. | l | ||||||
ср t . | |||||||
Путь – это то расстояние, которое газ проходит по трубе. | |||||||
V = sl | V | ||||||
l s . | |||||||
Запишем для газа уравнение Клапейрона – Менделеева. | |||||||
pV | m | RT | mRT | ||||
V Mp . | |||||||
M | |||||||
Теперь найдем среднюю скорость движения газа в трубе: | |||||||
ср l | V | mRT . | |||||
t | tS | tSMp | |||||
ср | 20 8,31 280 | 9 м / с . | |||||
600 5 105 | 44 10 3 3,92 105 | ||||||
Ответ: ср = 9 м/с

50
Пример 6.
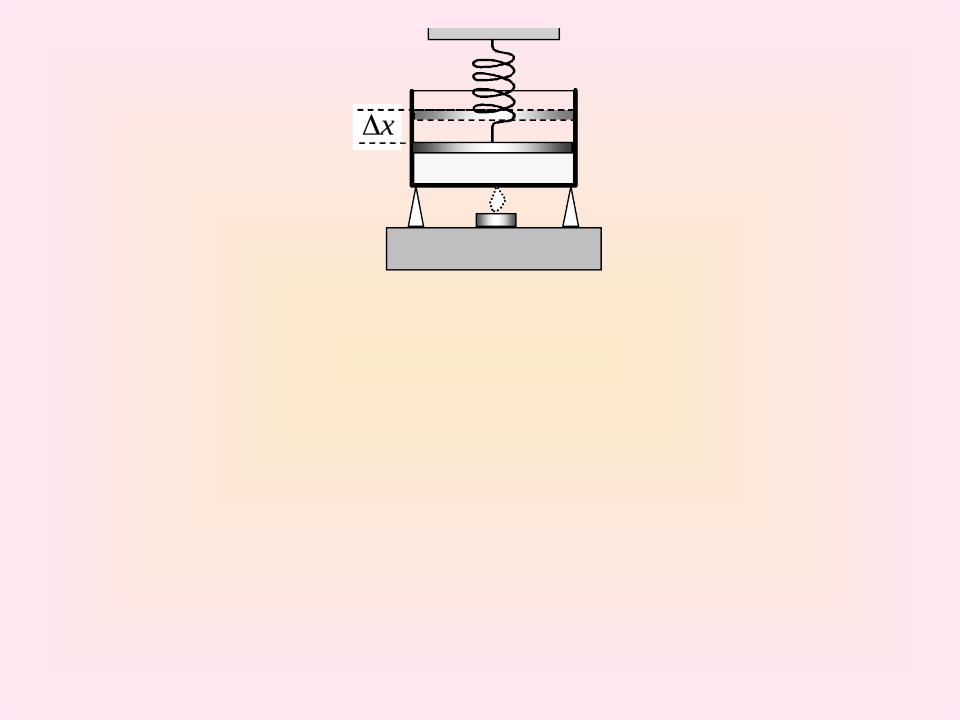
Цилиндр с поршнем содержит газ. Сверху поршень прижат идеальной пружиной. Цилиндр начинают нагревать (см. рисунок). Объем газа изменяется от V1 до V2, а давление от р1 до р2. Определите совершаемую при этом работу газа. Вычисления провести при следующих параметрах:
р1 = 1 105 Па; р2 = 2 105 Па; V1 = 1 л; V2 = 3 л. Ответ
представьте в единицах СИ.
Дано: р1 = 1 105 Па, р2 = 2 105 Па, V1 = 1 л = 10-3 м3, V2 = 3 л = 2 10-3 м3
Найти: А.
51
Так как в системе меняются все параметры: p, V и Т, то работу газа удобнее рассчитать графически (см. предыдущую задачу). По определению давление определяется формулой:
p Fs Fупр = ps.
Но по закону Гука сила упругости определяется следующим выражением:
Fупр = k x.

52
ps = k x | p | k x | , | ||||||||||||||||||||||||||||||||||||||||||||
s | |||||||||||||||||||||||||||||||||||||||||||||||
где x – перемещение поршня, которое можно определить через | |||||||||||||||||||||||||||||||||||||||||||||||
объем. | V = s x | V | |||||||||||||||||||||||||||||||||||||||||||||
x s . | |||||||||||||||||||||||||||||||||||||||||||||||
p k x | k V | const V, | |||||||||||||||||||||||||||||||||||||||||||||
s | s2 | ||||||||||||||||||||||||||||||||||||||||||||||
то есть давление газа в цилиндре | p | 2 | |||||||||||||||||||||||||||||||||||||||||||||
изменяется | пропорционально | ||||||||||||||||||||||||||||||||||||||||||||||
объему: p V. | p2 | ||||||||||||||||||||||||||||||||||||||||||||||
Тогда в pV – координатах график | p1 | 1 | |||||||||||||||||||||||||||||||||||||||||||||
будет | выглядеть | аналогично | sтр | V | |||||||||||||||||||||||||||||||||||||||||||
графику, | представленному | в | |||||||||||||||||||||||||||||||||||||||||||||
предыдущей | задаче. Тогда работу | ||||||||||||||||||||||||||||||||||||||||||||||
V1 | V 2 | ||||||||||||||||||||||||||||||||||||||||||||||
определим через площадь трапеции. | |||||||||||||||||||||||||||||||||||||||||||||||

53
A sтр a b h,
2
A p1 p2 V2 V1 .
2
A 105 2 105 3 10 3 10 3 300 Дж . 2
Ответ

54
Пример 7. Найдите число молекул водорода в 1 см3, если давление равно 200 мм.рт.ст., а средняя квадратичная скорость молекул при данных условиях 2400 м/с.
Дано:
V = 1 м3  p= 200 мм.рт.ст. = 200 133.3 Па
p= 200 мм.рт.ст. = 200 133.3 Па
< кв> = 2400 м/с
k = 1,38 10-23Дж/К R = 8,31 Дж/моль К
Найти: n.

55
Решение: Искомая величина может быть найдена из соотношения
р = nkT.
n kTp .
Средняя квадратич

