Два сосуда наполнены водой до разных уровней

>>> Перейти на мобильную версию сайта >>>
Учебник для 10 класса
Физика
Термодинамика
При решении задач по этой теме надо иметь в виду, что давление и плотность насыщенного пара не зависят от объема, а зависят только от температуры.
Давление насыщенного пара считается известной величиной (сообщается в условии задачи или находится в соответствующих таблицах).
Уравнение состояния идеального газа вдали от критической температуры приближенно применимо для описания насыщенного пара. Но при сжатии или нагревании насыщенного пара его масса изменяется.
Задача 1
В замкнутом сосуде объемом V = 1 м3 находится вода массой m = 12 г и насыщенный пар; плотность и давление пара при данной температуре равны соответственно р = 8 • 10-3 кг/м3 и р = 1,1 кПа. Какое давление установится при увеличении объема в k = 5 раз? Считать, что температура при увеличении объема не изменяется.
Решение. В сосуде первоначально содержался насыщенный пар массой m1 = ρV = 8 • 10-3 кг (объемом, занимаемым водой, можно пренебречь).
Масса воды и пара была равна m + m1 = 2 • 10-2 кг. Для насыщения объема, равного kV, необходим пар массой m2 = ρkV = 4 • 10-2 кг. Так как m + m1 < m2, то после увеличения объема пар станет ненасыщенным. Его плотность .
Давление пара при данной температуре прямо пропорционально плотности. Поэтому
Задача 2
В закрытом сосуде объемом V1 = 0,5 м3 находится вода массой m = 0,5 кг. Сосуд нагрели до температуры t = 147 °С. На какую величину AV следует изменить объем сосуда, чтобы в нем содержался только насыщенный пар? Давление насыщенного пара при температуре t = 147 °С равно р0 = 4,7 • 105 Па.
Решение. Насыщенный пар при давлении р0 занимает объем
где М = 0,018 кг/моль — молярная масса воды. Объем сосуда V1 > V и пар не является насыщенным. Чтобы пар стал насыщенным, объем сосуда следует изменить на
Объем сосуда должен быть уменьшен на 0,3 м3.
Задача 3
Кусок алюминия массой m1 = 537 г, нагретый до температуры t1 = 200 °С, опустили в воду массой m2 = 400 г при температуре t2 = 16 °С. Вода нагрелась до температуры t = 50 °С и частично испарилась. Определите массу испарившейся воды. Удельная теплоемкость алюминия с1 = 920 Дж/(кг • К). Удельная теплоемкость воды с1 = 4200 Дж/(кг • К), а удельная теплота парообразования воды при температуре кипения (tK = 100 °С) равна г = 2,26 МДж/кг. Тепловыми потерями пренебречь.
Решение. Количество теплоты, отданное куском алюминия:
Количество теплоты, полученное водой, складывается из количества теплоты, полученного всей водой при нагревании от t2 до t:
и количества теплоты, израсходованного для нагревания части воды массой m3 от t до tK и ее испарения при этой температуре:
Пренебрегая тепловыми потерями, запишем уравнение теплового баланса:
или
Откуда
Задача 4
Пористое тело было помещено для просушки под колокол вакуумного насоса. Давление под колоколом держалось на уровне 6,5 мм рт. ст. в течение 1 ч, после чего резко упало. Подача насоса 60 л/мин. Установившаяся под колоколом насоса температура t = 5 °С. Сколько воды содержало тело?
Решение. Давление р = 6,5 мм рт. ст. — это давление насыщенных водяных паров при t = 5 °С. Резкое падение давления свидетельствует о том, что вся вода превратилась в пар. Объем пара, откачанного насосом до полного испарения воды, V = 3600 л. Пользуясь уравнением состояния Менделеева— Клапейрона, находим искомую массу воды
Задача 5
В сосуде находится воздух, относительная влажность которого при температуре t1 = 10 °С равна (φ1 = 60%. Какой будет относительная влажность φ2 после уменьшения объема сосуда в n раз (n = 3) и нагревания газа до температуры t2 = 100 °С? Плотность насыщенных водяных паров при температуре t1 равна ρ = 9,4 • 10-3 кг/м3.
Решение. При температуре t1 абсолютная влажность (до сжатия) равна ρ1 = φ1ρ. После сжатия масса влаги, приходящаяся на единицу объема сосуда (не только в виде паров, но и в виде сконденсировавшейся жидкости, если возникли условия для конденсации), будет равна ρ2 = nφ1ρ = 1,69 • 10-2 кг/м3.
При температуре t2 = 100 °С давление насыщенных водяных паров равно нормальному атмосферному давлению р0 = 105 Па, и их плотность
Так как ρ3 > ρ2. то в сосуде будет ненасыщенный пар с относительной влажностью
Упражнение 5
- Почему капельки воды на разогретой сковородке «крутятся» на ней более минуты, прежде чем исчезнуть?
- В колбе кипятят воду. Затем колбу снимают с огня и закупоривают резиновой пробкой. Если теперь охладить колбу, облив ее холодной водой, то вода в колбе закипает. Почему?
- Два полых, герметически запаянных шара, в одном из которых вода, соединены трубкой (рис. 6.20). Воздух из шаров откачан. Если пустой шар поместить в сосуд с жидким воздухом, то вода в другом шаре быстро замерзнет. Объясните явление.

Рис. 6.20
- На улице целый день моросит холодный осенний дождь. В комнате развешено выстиранное белье. Высохнет ли белье быстрее, если открыть форточку?
- На рисунке 6.21 изображен прибор, называемый кипятильником Франклина. Этот прибор состоит из двух полых стеклянных шаров, соединенных трубкой. В прибор налито некоторое количество спирта и откачан воздух. Если прибор слегка наклонить, то спирт соберется в одном (левом) шаре (см. рисунок). Обхватив этот шар ладонью, мы увидим, что спирт быстро перейдет в другой (правый) шар, хотя он расположен немного выше, и будет в нем бурлить, подобно кипящей воде. Объясните явление.

Рис. 6.21
- Можно ли газ, имеющий температуру ниже критической, перевести непрерывным путем (минуя состояние равновесия между жидкостью и газом) в жидкость той же температуры?
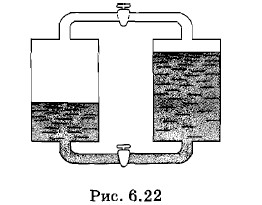
- Два сосуда, соединенных трубками с кранами, наполнены водой до разных уровней (рис. 6.22). Воздух из сосудов откачан. Что произойдет, если соединить сосуды, открыв кран: 1) в нижней трубке; 2) в верхней трубке?

Рис. 6.22
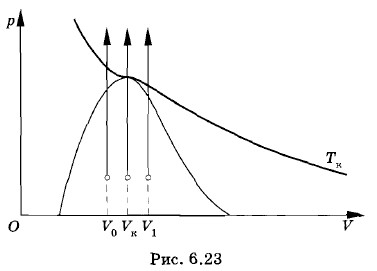
- Опишите, что будет происходить с веществом, если его нагревать при постоянных объемах сосудов VQ, VK и V1 (рис. 6.23).

Рис. 6.23
- Сравните качественно температуру кипения и удельную теплоту парообразования воды в глубокой шахте и на поверхности Земли.
- Почему в момент выключения газовой горелки из кипящего чайника сразу же вырывается струя пара, хотя до этого пара не было видно?
- В котел объемом V = 5 м3 накачали воду массой m1 = 20 кг и нагрели содержимое котла до температуры t = 180 °С. Найдите массу m2 и давление р пара в котле. Плотность насыщенного водяного пара при температуре Т = 453 К равна р = 5,05 кг/м3. Молярная масса воды М = 0,018 кг/моль.
- В цилиндре под поршнем в объеме V1 = 1 м3 при температуре t = 30 °С находится смесь азота и насыщенного пара воды. Масса смеси m0 = 286 г. Какая масса пара сконденсируется, если объем уменьшить в n раз (n = 3) при постоянной температуре? Какое давление р было у смеси до сжатия? Давление насыщенного водяного пара при температуре 30 °С равно р1 = 4,2 кПа. Молярные массы воды и азота равны соответственно М1 = 0,018 кг/моль и М2 = 0,028 кг/моль.
- До какой температуры нагреется вода объемом 0,8 л, находящаяся в медном калориметре массой 0,7 кг и имеющая температуру 285 К, если ввести в калориметр пар массой 0,05 кг при температуре 373 К? Удельная теплоемкость воды 4,2 кДж/(кг • К); удельная теплоемкость меди 0,38 кДж/(кг • К); удельная теплота парообразования воды 2,26 МДж/кг.
1
- Через змеевик нагревателя, содержащего 12 л воды при температуре 12 °С, пропускают стоградусный водяной пар. Вытекающая из змеевика вода (конденсат) имеет температуру 60 °С. Какое количество пара нужно пропустить через змеевик, чтобы температура воды в нагревателе повысилась до 50 °С?
- Определите абсолютную влажность воздуха, если парциальное давление пара в нем р = 14 кПа, а температура t = 60 °С.
- В комнате, объем которой V = 100 м3, температура воздуха понизилась от t1 = 25 °С до t2 = 15 °С. Сколько водяных паров при этом сконденсировалось из воздуха, первоначально находившегося в комнате, если плотность насыщенного водяного пара при 25 °С равна р1 = 23 г/м3, а при 15 °С — р2 = 12,8 г/м3? Относительная влажность воздуха вначале была равна φ = 90%.
- В здание необходимо подать 100 000 м3 воздуха при температуре 20 °С и относительной влажности 70%. Воздух забирают с улицы, где он имеет температуру -5 °С и относительную влажность 90%. Давление насыщенных водяных паров при -5 °С равно 400 Па, а при 20 °С — 2,33 кПа. Сколько воды надо дополнительно испарить в подаваемый воздух?
- После понижения температуры от 27 до 10 °С оказалось, что из каждого кубического метра воздуха выделилось 8 г воды. Какова была относительная влажность воздуха при 27 °С? Давление насыщенного водяного пара при 27 °С равно 3,56 кПа, а при 10 °С — 1,23 кПа.
Источник
Глава 6. Взаимные превращения жидкостей и газов
1. Почему капельки воды на разогретой сковородке «крутятся» на ней более минуты, прежде чем исчезнуть?
2. В колбе кипятят воду. Затем колбу снимают с огня и закупоривают резиновой пробкой. Если теперь охладить колбу, облив ее холодной водой, то вода в колбе закипает. Почему?
3. Два полых, герметически запаянных шара, в одном из которых вода, соединены трубкой (рис. 6.20). Воздух из шаров откачан. Если пустой шар поместить в сосуд с жидким воздухом, то вода в другом шаре быстро замерзнет. Объясните явление.
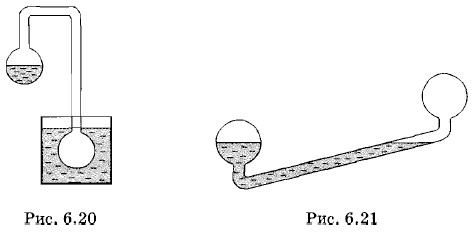
4. На улице целый день моросит холодный осенний дождь.
В комнате развешено выстиранное белье. Высохнет ли белье быстрее, если открыть форточку?
5. На рисунке 6.21 изображен прибор, называемый кипятильником Франклина. Этот прибор состоит из двух полых стеклянных шаров, соединенных трубкой. В прибор налито некоторое количество спирта и откачан воздух. Если прибор слегка наклонить, то спирт соберется в одном (левом) шаре (см. рисунок). Обхватив этот шар ладонью, мы увидим, что спирт быстро перейдет в другой (правый) шар, хотя он расположен немного выше, и будет в нем бурлить, подобно кипящей воде. Объясните явление.
6. Можно ли газ, имеющий температуру ниже критической, перевести непрерывным путем (минуя состояние равновесия между жидкостью и газом) в жидкость той же температуры?
7. Два сосуда, соединенных трубками с кранами, наполнены водой до разных уровней (рис. 6.22). Воздух из сосудов откачан. Что произойдет, если соединить сосуды, открыв кран: 1) в нижней трубке; 2) в верхней трубке?
8. Опишите, что будет происходить с веществом, если его нагревать при постоянных объемах сосудов F0, VK и V1 (рис. 6.23).
9. Сравните качественно температуру кипения и удельную теплоту парообразования воды в глубокой шахте и на поверхности Земли.
10. Почему в момент выключения газовой горелки из кипящего чайника сразу же вырывается струя пара, хотя до этого пара не было видно?
11. В котел объемом V = 5 м3 накачали воду массой m1 = 20 кг и нагрели содержимое котла до температуры t = 180 °С. Найдите массу m2 и давление р пара в котле. Плотность насыщенного водяного пара при температуре Т = 453 К равна ρ = 5,05 кг/м3. Молярная масса воды М = 0,018 кг/моль.
12. В цилиндре под поршнем в объеме V1 = 1 м3 при температуре t = 30 °С находится смесь азота и насыщенного пара воды. Масса смеси m0 = 286 г. Какая масса пара сконденсируется, если объем уменьшить в n раз (n = 3) при постоянной температуре? Какое давление р было у смеси до сжатия? Давление насыщенного водяного пара при температуре 30 °С равно р1 = 4,2 кПа. Молярные массы воды и азота равны соответственно М1 = 0,018 кг/моль и М2 = 0,028 кг/моль.
13. До какой температуры нагреется вода объемом 0,8 л, находящаяся в медном калориметре массой 0,7 кг и Имеющая температуру 285 К, если ввести в калориметр пар массой 0,05 кг при температуре 373 К? Удельная теплоемкость воды 4,2 кДж/(кг • К); удельная теплоемкость меди 0,38 кДж/(кг • К); удельная теплота парообразования воды 2,26 МДж/кг.
14. Через змеевик нагревателя, содержащего 12 л воды при температуре 12 °С, пропускают стоградусный водяной пар. Вытекающая из змеевика вода (конденсат) имеет температуру 60 °С. Какое количество пара нужно пропустить через змеевик, чтобы температура воды в нагревателе повысилась до 50 °С?
15. Определите абсолютную влажность воздуха, если парциальное давление пара в нем р = 14 кПа, а температура t = 60 °С.
16. В комнате, объем которой V = 100 м3, температура воздуха понизилась от t1 = 25 °С до t2 = 15 °С. Сколько водяных паров при этом сконденсировалось из воздуха, первоначально находившегося в комнате, если плотность насыщенного водяного пара при 25 °С равна ρ1 = 23 г/м3, а при 15 °С — ρ2 = 12,8 г/м3? Относительная влажность воздуха вначале была равна φ = 90%.
17. В здание необходимо подать 100 000 м3 воздуха при температуре 20 °С и относительной влажности 70%. Воздух забирают с улицы, где он имеет температуру -5 °С и относительную влажность 90%. Давление насыщенных водяных паров при -5 °С равно 400 Па, а при 20 °С — 2,33 кПа. Сколько воды надо дополнительно испарить в подаваемый воздух?
18. После понижения температуры от 27 до 10 °С оказалось, что из каждого кубического метра воздуха выделилось 8 г воды. Какова была относительная влажность воздуха при 27 °С? Давление насыщенного водяного пара при 27 °С равно 3,56 кПа, а при 10 °С — 1,23 кПа.
Источник
https://vk-blog.com/gidravlika-r-87/
Часть задач есть решенные, https://vk.com/id5150215
Задача 1
Определить изменение плотности жидкости (ρ = 1000 кг/м3) при изменении давления от р1 = 1 · 105 Па до р2 = 1 · 107 Па.
Задача 2
Определить плотность жидкости, полученной смешиванием 15 л жидкости плотностью ρ1 = 720 кг/м3 и 25 л жидкости плотностью ρ2 = 1000 кг/м3.
Задача 3
Каким должен быть объем нефтехранилища для размещения нефти массой 60 т, удельным весом γ = 8500 Н/м3?
Задача 4
Определить динамический коэффициент вязкости жидкости и ее относительный вес, если вязкость, определенная при помощи вискозиметра Энглера, равна 18,5°Е. Удельный вес жидкости принять γ = 8,84 кН/м3.
Задача 5
Стальной трубопровод, заполненный водой при t1 = 10 °С, находится под давлением p = 2 · 106 Па. Диаметр трубопровода d = 0,4 м, длина 1 км. Определить давление воды в трубопроводе при повышении температуры до t2 = 15 °С.
Задача 6
В цилиндрическом резервуаре высотой 6 м находится бензин (βt = 0,0008°С-1). При температуре t1= 15°С бензин не доходит до края на 10 см. Определить, при какой температуре бензин начнет переливаться через край резервуара.
Задача 7
При гидравлическом испытании участка трубопровода диаметром 400 мм и длиной 600 м давление воды в трубе было повышено до 2,943 МПа. Через час оно снизилось до 1,962 МПа. Сколько воды вытекло через неплотности, если коэффициент объемного сжатия воды βр = 5 · 10-10 Па-1?
Задача 8
При заполнении объемного гидропривода рабочая жидкость (масло) имеет температуру t1 = 15 °C. Определить температуру t2, которую может приобрести масло в процессе работы, чтобы давление в системе гидропривода повысилось не более чем на Δp = 40 МПа. Вместимость системы (объем масла до его нагревания) Wн = 20 л, βt = 0,0009 °C-1, E = 1390 МПа. (Считать, что гидропривод заполнен маслом полностью, расширительные резервуары отсутствуют, деформацию элементов гидропривода не учитывать).
Задача 9
Две плоские стеклянные пластины опущены нижними концами в воду параллельно друг другу (рис. 10), расстояние между ними d = 0,2 мм. Определить дополнительное давление, возникающее в воде от действия сил поверхностного натяжения рпов, а также высоту h, на которую поднимется жидкость между пластинами. Коэффициент поверхностного натяжения воды принять равным 7,2 · 10-2 Н/м.
Задача 10
Капиллярная трубка (рис. 11) с внутренним диаметром 1 мм наполнена водой. Часть воды повисла внизу в виде капли, которую можно принять за часть сферы радиусом 5 мм. Определить дополнительные давления рдоп1 и рдоп2, возникающие от действия сил поверхностного натяжения, искривляющие верхние и нижние мениски. Чему будут равны эти давления, если вместо воды в капилляре будет находиться: спирт; бензин? Температуру жидкостей принять равной 20°С.
1. ГИДРОСТАТИКА
1.1. Гидростатическое давление. Методы и средства для измерения давления
Задача 1
В герметически закрытом сосуде (рис. 1.15) налиты две несмешивающиеся жидкости до уровня h3 = 7 м. Показание манометра, установленного в верхней части сосуда, p = 16 кПа. Удельный вес жидкости, образующей верхний слой γ1 = 8 кН/м3, толщина этого слоя h1 = 3 м. Удельный вес жидкости нижнего слоя γ2 = 10 кН/м3. На глубине h2 = 5 м от свободной поверхности жидкости в сосуде присоединен открытый пьезометр. Определить высоту hх, на которую поднимется жидкость в пьезометре. Чему будет равно избыточное давление на дне сосуда?
Задача 2
Два герметичных сосуда (рис. 1.16) наполнены жидкостями с удельными весами γ1 = 10 кН/м3 и γ2 = 12 кН/м3 на высоту h1 = 1 м и h2 = 2 м соответственно. Сосуды соединены изогнутой трубкой, частично заполненной жидкостями из сосудов. Между точками А и В находится воздух. Уровень свободной поверхности жидкости γ1 в ле вой ветви трубки относительно основания сосудов h3 = 0,4 м. Вертикаль ное расстояние между точками А и В h4 = 1 м. В верхних точках сосудов установлены манометры. Показание первого манометра р1 =5 кПа. Чему равно показание второго манометра р2, а также избыточное давление воздуха в точках А и В?
Задача 3
Две запаянные с одного конца трубки и заполненные жидкостями с удельными весами γ1 = 11 кН/м3 и γ2 = 10 кН/м3, опрокинуты в открытые сосуды с теми же жидкостями (рис. 1.17). В запаянных трубках жидкость поднялась на высоту h1 и h2, соответственно. Принимая давление паров рассматриваемых жидкостей равным нулю, определить величину атмосферного давления, если разность высот столбов этих жидкостей составляет 0,9 м. Как изменится разность уровней жидкостей в трубках, если атмосферное давление повысится на 2%?
Задача 4
Герметически закрытый сосуд (рис. 1.18) наполнен жидкостью с удельным весом γ1 до высоты h1 = 2 м. Избыточное давление в верхней части сосуда, измеренное манометром, p = 100 кПа. От сосуда отходит изогнутая трубка, заполненная жидкостью с удельным весом γ1, ртутью (ρрт = 13600 кг/м3) и жидкостью с удельным весом γ2 = 12 кН/м3. Высота уровней жидкостей в трубке h2 = 0,8 м, h3 = 1,5 м, h4 = 3,5 м. Определить удельный вес жидкости γ1.
Задача 5
Две трубы, заполненные жидкостями γ1 = 10 кН/м3 и γ2 = 15 кН/м3, соединены изогнутой трубкой, частично заполненной ртутью γ3 = 133,4 кН/м3 (рис. 1.19). Определить разность давлений Δр = р2 – р= в центрах этих труб, расположенных в одной горизонтальной плоскости, если уровень ртути в правой ветви находится на высоте h1 = 0,5 м, а разность уровней ртути h2 = 2 м.
Задача 6
Герметично закрытый сосуд на высоту h1 = 1,5 м заполнен жидкостью, имеющей удельный вес γ1 = 10 кН/м3 (стр. 1.20). От дна сосуда отходит изогнутая трубка, заполненная в нижней части ртутью (γ2 = 133,4 кН/м3). Уровень ртути в правой ветви трубки находится ниже дна сосуда на h2 = 1,2 м. Разность уровней ртути h3 = 0,8 м. Над ртутью в левой ветви находится жидкость, плотность которой ρ3 = 2000 кг/м3. Показание манометра, установленного на крышке сосуда р = 127,72 кПа. Определить высоту столба жидкости h4 над ртутью в левой ветви.
Задача 7
Два герметичных сосуда (рис. 1.21), основания которых расположены на одной горизонтальной плоскости, наполнены жидкостями, имеющими разные удельные веса γ1 = 20 кН/м3 и γ2 = 10 кН/м3, на высоту h1 = 2 м и h2 = 1 м. Сосуды соединены изогнутой трубкой, в которой между точками А и В находится воздушный пузырь. Нижний край пузыря расположен на высоте h3 = 0,8 м над основанием сосуда. Определить положение верхнего края пузыря hх, если показания манометров на крышках сосудов р1 = 100 кПа, р2 = 78 кПа. Чему равно избыточное давление в точках А и В?
Задача 8
Два резервуара установлены на одной горизонтальной плоскости (рис. 1.22), соединены изогнутой трубкой, в которой между точками А и В находится газовый пузырь. Показание манометра левого резервуара, установленного на высоте h1 = 1 м над плоскостью оснований резервуаров, р1 = 100 кПа, уровень жидкости в пьезометре правого резервуара h2 = 4,75 м. Жидкость в левом резервуаре имеет удельный вес γ1 = 10 кН/м3, в правом — γ2 =20 кН/м3. Определить положение верхнего края пузыря hх, если его нижний край находится на высоте h3 = 1 м от оснований резервуаров.
Задача 9
Два сосуда (рис. 1.23), основания которых расположены в одной горизонтальной плоскости, наполнены разными жидкостями с удельными весами γ1 = 10 кН/м3, γ2 = 20 кН/м3, соединены изогнутой трубкой, в которой между жидкостями находится ртуть (γ3 = 133,4 кН/м3). В левом сосуде на высоте h1 = 3 м над плоскостью основания установлен манометр, показывающий давление р1 = 100 кПа. На крышке правого сосуда установлен манометр, его показание р2 = 192,72 кПа. Уровень жидкости в правом сосуде h2 = 1 м над плоскостью оснований. Определить разность уровней ртути hх, если ее верхний уровень находится на h3 = 0,8 м ниже плоскости оснований сосудов.
Задача 10
Герметично закрытый резервуар (рис. 1.24) заполнен водой до уровня h1 = 2,6 м относительно основания резервуара. Слева к резервуару присоединен пьезометр, уровень воды в котором относительно основания резервуара H. Справа к резервуару присоединена изогнутая трубка, заполненная водой и ртутью, уровни которых расположены на высоте h2 = 0,6 м, h3 = 1,6 м, h4 = 0,8 м, h5 = 1,8 м от основания сосуда. Плотность ртути ρ = 13 600 кг/м3.
Определить избыточное давление р0 воздуха в напорном баке. Какой высоты H должен быть пьезометр для измерения того же давления р0? Как изменится высота H, если р0 увеличится на 10%?
1.1.1
Задача 1
Пренебрегая разностью высот гидросистемы (рис. 1.33), определить показание манометра p и вес груза G, лежащего на поршне 2, если для его подъема к поршню 1 приложена сила F = 1,8 кН. Диаметры поршней: D = 255 мм, d = 68 мм. Разностью высот пренебречь.
Задача 2
Определить избыточное давление жидкости р1 фиксируемое манометром, которое необходимо подвести к гидроцилиндру (рис. 1.34), чтобы преодолеть усилие, направленное вдоль штока F = 0,85 кН. Диаметры: цилиндра – D = 41 мм, штока – d = 16 мм. Давление в бачке р0 = 41 кПа, высота Н0 = 4,55 м. Силу трения не учитывать. Плотность жидкости ρ = 1000 кг/м3.
Задача 3
Определить давление р в верхнем цилиндре гидропреобразователя (мультипликатора) (рис. 1.35), если показание манометра, присоединенного к нижнему цилиндру, рм = 0,35 МПа. Поршни перемешаются вверх, причем сила трения составляет 10 % силы давления жидкости на нижний поршень. Вес поршней G = 3,7 кН. Диаметры поршней: D = 370 мм, d = 75 мм; высота Н = 2 м; плотность масла ρ = 900 кг/м3.
Задача 4
Определить показание мановакуумметра pмв, если к штоку поршня (рис. 1.36) приложена сила F = 0,95 кН, его диаметр D = 85 мм, высота Н = 0,98 м, плотность жидкости ρ = 800 кг/м3.
Задача 5
Определить силу F, действующую на шток гибкой диафрагмы (рис 1.37), если ее диаметр D = 225 мм, показание вакуумметра pвак = 10 кПа, высота h = 1,2 м. Площадью штока пренебречь. Найти абсолютное давление в левой полости, если hатм = 760 мм рт. ст.
Задача 6
Определить силу F на штоке золотника (рис. 1.38), если показание вакуумметра pвак = 43 кПа, избыточное давление p1 = 0,68 МПа, высота h = 2,65 м, диаметры поршней D = 60 мм и d = 17 мм, ρ = 990 кг/м3.
Задача 8
При подъеме груза (рис. 1.40) массой 6 т на высоту 0,45 м воспользовались гидравлическим домкратом с кпд 75%. Отношение площадей большого поршня к малому ω1/ω2 = D2/d2 = 100, ход малого поршня 0,2 м. Сколько ходов сделает малый поршень для подъема груза? Какое максимальное усилие F необходимо приложить к рукоятке при ходе нагнетания, если a/b = 10? Весами обоих поршней пренебречь.
Задача 10
С какой силой каждая из тормозных колодок 1 (рис. 1.42) будет прижиматься к тормозному барабану 2 колеса, если сила нажатия на малый поршень F = 850 Н? Диаметр малого поршня d = 310 мм, больших поршней D = 390 мм.
1.2. Сообщающиеся сосуды. Закон Паскаля
Задача 1
Стеклянная трубка (рис. 1.58) с одной стороны закрыта пластиной и опущена этим концом вертикально в воду на глубину 0,68 м. Какой высоты нужно налить в трубку ртуть или керосин, чтобы пластика отпала?
Задача 2
В вертикальной перегородке закрытого резервуара (рис. 1.59) прямоугольная крышка шириной b = 0,4 м и высотой h = 0,5 м перекрывает отверстие. Правый отсек заполнен нефтью (ρ = 870 кг/м3) под избыточным давлением 12 кПа, левый — воздухом. Показание ртутною мановакуумметра, подключенного к левому отсеку резервуара, hрт = 60 мм. Определить значение и точку приложения силы давления нефти на крышку, если ее центр тяжести расположен на глубине Н = 0,75 м от свободной поверхности нефти. Атмосферное давление принять 100 кПа.
Задача 3
Открытый резервуар заполнен тремя несмешивающимися жидкостями (рис. 1.60), имеющими удельный вес и высоту слоя соответственно γ1 = 7,8 кН/м3, h1 = 1 м; γ2 = 9,81 кН/м3, h2 = 0,7 м; γ3 = 133,4 кН/м3, h3 = 0,3 м. Определить силу избыточного давления на наклонную (α = 60°) боковую стенку резервуара, если ее ширина b = 2 м. Расчет выполнить графоаналитическим методом, построив эпюры давления.
Задача 4
Определить натяжение каната Т, удерживающего затвор (рис. 1.61), который закрывает круглое отверстие r = 1 м в плоской наклонной стенке, если заданы следующие линейные размеры: H = 3м; l = 1,8ми углы α1 = α2 = 60º.
Задача 5
Определить результирующую силу избыточного давления воды, действующую на плоскую ломаную стенку (рис. 1.62) шириной b = 2 м; глубина воды h = 2 м, высота нижней части стенки h1 = 1 м, угол наклона верхней части стенки к горизонтальной плоскости α = 45°. Давление на свободную поверхность жидкости – атмосферное. Построить эпюру избыточного давления воды на стенку и найти координату центра давления стенки.
Задача 6
Четыре стенки, наклоненные к горизонтальной плоскости под углом 90°, 60°, 45° и 30° соответственно, показаны на рис. 1.63. Ширина каждой из стенок b = 1 м. Определить силу гидростатического давления воды на каждую из стенок, если уровень воды h = 1 м; на свободную поверхность воды действует атмосферное давление. На каком вертикальном расстоянии от свободной поверхности находится центр давления?
Задача 7
Промежуточная вертикальная стенка делит емкость (рис. 1.64) шириной b = 1,2 м на два отсека. Определить значение равнодействующей сил избыточного гидростатического давления на эту стенку и точку ее приложения, а также точки приложения сил P1 и P2, если уровень воды в левом отсеке h1 = 1200 мм, а в правом – h2 = 480 мм.
Задача 8
Щит, перекрывающий ирригационный канал, расположен под углом α = 45° к горизонту и прикреплен шарнирно к опоре над водой (рис. 1.65). Пренебрегая весом щита и трением в шарнире, определить усилие, которое необходимо приложить к тросу для открывания щита, если его ширина b = 1,5 м, глубина воды перед щитом h1 = 3 м, за щитом h2 = 2 м. Шарнир расположен на расстоянии h3 = 1,5 м над высшим уровнем воды.
Задача 9
Емкость, наполненная жидкостью с плотностью ρ = 750 кг/м3, имеет форму перевернутой вершиной вниз пирамиды (рис. 1.66). Определить силы давления жидкости, действующие на каждую грань емкости, если рм = 200 кПа, Н = 5 м, h = 1,5 м и стороны основания пирамиды: а = 1,1 м; b = 0,8 м.
Задача 10
Определить силу давления масла (γ = 8650 Н/м3) на болты крышки (рис. 1.67), которая имеет форму прямоугольника высотой a = 0,64 м и шириной b = 1,5 м. Показание манометра рм = 120 кПа, высота h = 2 м.
Задача 11
В нижней части вертикальной плоской стенки открытого резервуара имеется проем прямоугольной формы шириной b = 4 м, закрытый криволинейной крышкой ab в виде четверти боковой поверхности цилиндра радиусом r = 1 м (рис. 1.68). Глубина воды в резервуаре h = 3 м.
Определить значение и направление действия силы P давления воды на крышку.
Задача 12
Металлическая цистерна диаметром d = 1,8 м и длиной l = 10 м полностью заполнена минеральным маслом γ = 9000 Н/м3 (рис. 1.69). Давление на поверхности масла – атмосферное. Чему равна сила избыточного давления масла на внутреннюю поверхность цистерны abc?
Задача 13
Определить значение и направление действия силы гидростатического давления бензина (γ = 7,6 кН/м3) на полуцилиндрическую крышку радиусом r = 1 м, закрывающую прямоугольное отверстие в вертикальной стенке герметично закрытого резервуара (рис. 1.70). Показание манометра, подключенного над свободной поверхностью бензина, рм = 15 кПа. Центр отверстия расположен на глубине h = 2 м от свободной поверхности.
Задача 14
Секторный затвор (рис. 1.71) радиусом r = 1,2 м закрывает донное отверстие прямоугольной формы в плотине. Определить значение и направление действия силы избыточного давления воды на затвор, если напор на плотине h = 5 м, ширина отверстия b = 2,5 м.
Задача 15
С какой силой жидкость (ρ = 800 кг/м3) воздействует на цилиндрическую крышку (рис. 1.72) радиусом r = 0,5 м и длиной l = 2 м, если избыточное давление на свободной поверхности pизб = 15 кПа?
Закрытый резервуар наполнен жидкостью на глубину h = 2,5 м?
Задача 17
Герметично закрытый резервуар (рис. 1.74) наполнен двумя несмешивающимися (ρ1 = 800 кг/м3, ρ2 = 1000 кг/м3) жидкостями на глубину h1 = 0,5 м и h2 = 1,6 м. На свободной поверхности жидкости избыточное давление равно 12 кПа. Определить значение и направление действия силы избыточного давления на полуцилиндрическую крышку диаметром d = 0,8 м, длиной l = 2,5 м, в вертикальной стенке резервуара.
Задача 19
Герметически закрытый резервуар наполнен жидкостью, имеющий плотность ρ = 870
Источник
