Два сосуда соединены тонкой трубкой краном

Порядок назначения третьего эксперта

1. Поскольку в указанном процессе газ не совершает работы и система является теплоизолированной, то в соответствии с первым законом термодинамики суммарная внутренняя энергия газов сохраняется:

где – температура в объединённом сосуде в равновесном состоянии после открытия крана.

2. В соответствии с уравнением Клапейрона – Менделеева для конечного состояния можно записать:

Исключая из двух записанных уравнений конечную температуру получаем искомое выражение для начальной температуры аргона:

Ответ: K

p V = p V ;

В соответствии с Порядком проведения государственной итоговой аттестации по образовательным программам среднего общего образования (приказ Минобрнауки России от зарегистрирован Минюстом России )

« По результатам первой и второй проверок эксперты независимо друг от друга выставляют баллы за каждый ответ на задания экзаменационной работы ЕГЭ с развёрнутым ответом…

В случае существенного расхождения в баллах, выставленных двумя экспертами, назначается третья проверка. Существенное расхождение в баллах определено в критериях оценивания по соответствующему учебному предмету.

Эксперту, осуществляющему третью проверку, предоставляется информация о баллах, выставленных экспертами, ранее проверявшими экзаменационную работу».

Если расхождение составляет и более балла за выполнение задания, то третий эксперт проверяет ответ на задание.

Критерии оценки

3 баллаПриведено полное решение, включающее следующие элементы:
I. записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: формула для заряда
конденсатора, закон сохранения заряда, выражение для энергии
конденсатора, ёмкости параллельно соединённых конденсаторов,
закон сохранения энергии);
II. описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);
III. проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
IV. представлен правильный ответ с указанием единиц измерения
искомой величины

2 баллаПравильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков.

Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ)
В решении имеются лишние записи, не входящие в решение
(возможно, неверные), которые не отделены от решения (не
зачёркнуты; не заключены в скобки, рамку и т.п.).
И (ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
И (ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе в
записи единиц измерения величины)

1 баллПредставлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
данной задачи, без каких-либо преобразований с их использованием,
направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения данной задачи (или утверждение, лежащее в основе
решения), но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной
задачи (или в утверждении, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования с
имеющимися формулами, направленные на решение задачи

0 балловВсе случаи решения, которые не соответствуют вышеуказанным
критериям выставления оценок в балла

Источник

Решение

pV = νRTx		0,72νRTx = νR(Tx − T);

1,2p 0,6V = νR(Tx − T);
0,72T	= (T − T);	T		=	T	=	84	= 300K;

x	x	x	0,28		0,28

149. В изохорном процессе давление идеального газа увеличивается на р = 50 кПа. На сколько при неизменной массе газа увеличится температура, если первоначальное давление составляло р1 = 200 кПа, а первоначальная температура Т1 = 300 К?

Решение

р1V = νRT1;				p	+ p	=	T	+	T	;
(p	+	p)V = νR(T		+	T);	=	1	p	1	;	T
1	1	1	1
1,25T1 = T1 +	T;	T = 0,25T1 = 75K;

150.При постоянной температуре давление идеального газа уменьшилось

в9 раз. Что при этом произошло с объемом газа?

Решение

1. Изотермический процесс удовлетворяет уравнению:

т.е. объём газа увеличится в 9 раз.

151. Два сосуда соединены тонкой трубкой с краном. В первом сосуде объёмом V1 = 15 дм3 находится газ под давлением р1 = 2 атм., во втором сосуде − такой же газ под давлением р2 = 10 атм. Если кран открыть, то в обоих сосудах устанавливается давление р0 = 4 атм. Найти в дм3 объём второго сосуда, считая температуру постоянной.

Решение

p1V1 = ν1RT;		ν = p1V1 ;
1	RT
p2V2		= ν2RT;	p0V1 + p0V2 = p1V1 − p2V2 ;
p (V + V )= (ν + ν			)RT;	ν2 =	p V	;
					2 2
0 1	2	1 2		RT

V = p0V1 − p1V1 = 15(4 − 2) = 5дм3;
2	p2 − p1	6

152. Под каким давлением надо наполнить воздухом баллон ёмкостью V1 = 10 л, чтобы при соединении его с баллоном ёмкостью V2 = 30 л, содержащим воздух при давлении р2 = 100 кПа, установилось давление р0 = 200 кПа Процесс протекает при постоянной температуре.

Два сосуда соединены тонкой трубкой краном

Решение
p1V1 = ν1RT;		ν = p1V1 ;
1	RT
p2V2		= ν2RT;			p0V1 + p0V2 = p1V1 + p2V2 ;
p (V + V )=		(ν + ν )RT;						ν2 =	p V	;
									2 2
0 1	2	1	2		RT

p V = p (V + V ) − p V ; p = p0 (V1 + V2 ) − p2V2											;
1	1	1	2	2	2	1	V1

p		=	2 105	40 −1 105 30					= 500 кПа ;

1	10

153. В помещении при относительной влажности ϕ = 0,6 парциальное давление водяного пара составляет pп =2400 Па. Определить давление насыщенного пара при данной температуре.

Решение
р	ϕ = р	;	р	=	рп =	2400	= 4000 Па;
нп	п	нп	ϕ	0,6

154.Определить абсолютную влажность воздуха при температуре t = 15 0С

иотносительной влажности ϕ = 0,8. Плотность насыщенного пара при данной температуре составляет ρнп = 12,8 г/м3.

Решение

ρп = ρнпϕ =10,24 мг3 ≡1,024 10−2 мкг3 ;

155. Воздушный шар имеет газонепроницаемую оболочку массой М = 400 кг и содержит m = 100 кг гелия. Какой груз он может удерживать на высоте, где температура воздуха t = 17 0С и давление р = 105 Па? Молярная масса воздуха μ1 = 0,029 кг/моль, молярная масса гелия μ2 = 0,004 кг/моль. Считать, что оболочка шара не оказывает сопротивления изменению объёма.

Решение

1. Объём воздушного шара:

pV =	m	RT;	V = mRT ;

μ2		pμ2

2.	Плотность воздуха при заданных условиях:
pV = m RT;		p =	m	RT;	p = ρ RT			; ρ =

μ	Vμ		μ
1	1		1
3.	Условие равновесия шара на заданной высоте:
pμ1	FA = (M + m + mx )g; ρgV = (M + m + mx
	g mRT = (M + m + mx )g;				m	μ1	= (M + m

RT	pμ2	μ2

mx = m μ1 − (M + m) =100 7,25 −500 = 225кг ;

μ2

156. Воздушный шар с газонепроницаемой оболочкой массой М = 400 кг заполнен гелием. На высоте, где температура окружающего воздуха составляет t = 17 0С и давление р = 105 Па, шар может удерживать массу mx = 225 кг. Какова масса гелия m в оболочке шара? Молярная масса воздуха μ1 = 0,029 кг/моль, молярная масса гелия μ2 = 0,004 кг/моль. Считать, что оболочка шара не оказывает сопротивления изменению объёма.

Решение

1. Объём воздушного шара:

pV =

RT;

V = mRT ;

μ2

pμ2

2. Плотность воздуха при заданных условиях:

; ρ = pμ1

pV = m RT; p =

RT;

p = ρ RT

;

Vμ

3. Условие равновесия шара на заданной высоте:

FA = (M + m + mx )g; ρgV = (M + m + mx )g;

pμ1

g mRT = (M + m + mx )g;

μ1

= (M + m + mx ) ;

pμ2

μ2

μ1

M + mx

= M + mx

; m =

;

μ2

− m = M + mx ; m

μ2

−1

μ1

−1

μ2

m= 6625,25 =100кг;

157.Воздушный шар объёмом V = 2500 м3 с массой оболочки М = 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой.

Какую максимальную массу может поднимать шар, если воздух в нём нагреть до температуры t2 = 77 0C при температуре окружающего воздуха t1 = 7 0C и

при плотности окружающего воздуха ρ1 = 1,2 кг/м3. Оболочку шара считать нерастяжимой.

Решение

Давление на заданных высоте и температуре:

pV = m RT ;

p = ρ

RT1

;

Плотность нагретого воздуха внутри шара:

pμ

= ρ1RT1

= ρ

;

1 T

Масса нагретого воздуха

= ρ

V = ρ

V 2400 кг;

1 T

Условие равновесия шара в заданных условиях:

ρ1Vg = (M + m2 + mx )g; mx = ρ1V − M − m2 ;

1,2 2500 − 2800 200 кг;

Два сосуда соединены тонкой трубкой краном

158. Воздушный шар объёмом V = 2500 м3 имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. Если температура окружающего воздуха t1 = 7 0С, а его плотность ρ1 = 1,2 кг/м3, то при нагревании воздуха в шаре до температуры t2 = 77 0С шар поднимает груз с максимальной массой mx = 200 кг. Какова масса оболочки? Оболочку шара считать нерастяжимой.

Решение

Давление на заданных высоте и температуре:

pV = m RT ;

p = ρ

RT1

;

Плотность нагретого воздуха внутри шара:

pμ

= ρ1RT1

= ρ

;

1 T

Масса нагретого воздуха

= ρ

V = ρ

V 2400 кг;

1 T

Условие равновесия шара в заданных условиях:

ρ1Vg = (M + m2 + mx )g; M = ρ1V − m2 − mx ;

1,2 2500 − 2600 400 кг;

159. В цилиндре под поршнем площадью s = 100 см2 находится m = 28 г азота при температуре Т1 = 273 К. Цилиндр нагревают до температуры Т2 = 373 К. На какую высоту поднимется поршень массой M = 100 кг? Атмосферное давление р0 = 105 Па, молярная масса азота μ = 2,8 10 − 3 кг/моль.

Решение

1.Количество вещества под поршнем:

ν= mμ =1 моль;

2.Давление азота под поршнем:

p = p0 + Mgs = 2 105 Па;;

3. При медленном изменении температуры давление под поршнем будет оставаться постоянным, потому что будет изменяться объём. Для

Рис. 159. Азот под поршнем одного моля газа уравнения состояния:

pV1	= RT1	;	V1 =	RT	; V2	=	RT	;
pV2		1		2
		p		p
	= RT2 ;

3. Разность объёмов представится следующим образом:

V − V =	hs =	R	T;	h =	R T	8,3 100	0,415м;
		p			ps	2 103
1 2

160. Температура воздуха в цилиндре t1 = 7 0С. На сколько переместится поршень при нагревании воздуха на Т = 20 К, если вначале расстояние от дна цилиндра до поршня было равным h1 = 0,14 м?

Два сосуда соединены тонкой трубкой краном

Решение

pV1	= νRT1;	V T			sh	T
pV2		1	=	1	;	=	1	; hT2	= hT1 = hT1;
		V2		T2			s(h +			h)	T2
	= νRT2 ;

h = h T = 0,14 20 =1 см; T1 280

161. В цилиндре под поршнем площадью s = 10 cм2 находится газ. Чтобы поршень оставался в покое при увеличении температуры газа в 2 раза на поршень нужно поставить дополнительный груз массой m = 10 кг. Чему было равно начальное давление?

pV = νRT;
	mg

p +	= νR2T;
s

Решение
p	=	1	; 2p = p + mg	; p = mg	=	10 10	=105 Па;
mg		2				10−3
	p +		s	s
s

162.Газ находится в вертикальном цилиндре массой M = 5 кг и площадью s

=10 − 3 м2. Груз какой массы нужно положить на поршень, чтобы он оставался в том же положении при увеличении температуры газа в 2 раза. Внешнее атмосферное давление нормальное.

Решение

+	Mg
	p0	s	V = νRT;

		Mg	mg
+				+	= νR2T;
	p0
	s	s

p0 +

p0s

;

m =

+ M;

m = 105 10−3 + 5 =15 кг; 10

Рис. 163. Откачанная трубка с ртутью

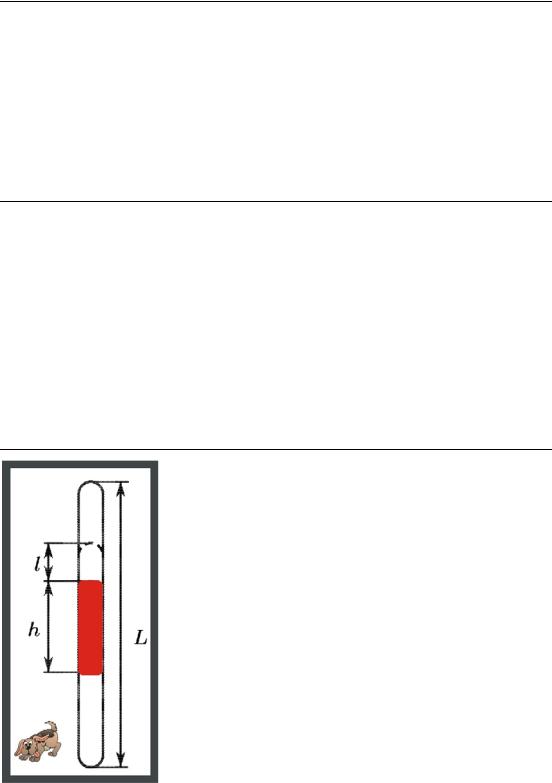
163. Посередине откачанной и запаянной с обоих концов горизонтально расположенной трубки длиной L находится столбик ртути длиной h. Если трубку поставить вертикально, то ртуть сместится на расстояние l. До какого давления р была откачана трубка?

Решение

1. При горизонтальном положении трубки давление по обе стороны ртути одинаково и равно р, объём тоже одинаков:

V = s(L – h); 2

2. При вертикальном положении трубки давления и объемы в частях разделенных ртутью будут разными, для верхней части трубки верхней части:

p ;	V	L − h
		= s	2	+ l ;
1	1

Два сосуда соединены тонкой трубкой краном

pV = p1V1; p(L − h)= p1(L − h + 2l)

3. Для нижней части трубки:

pV = p2V2 ; (L − h)p = p2 (L − h − 2l);

4. Условие равновесия столбика ртути при вертикальном положении труб-

ки:

p2 = p1 + ρgh ;

5. Подставим значение объёмов и давлений в уравнение p1V1 = p2V2 неизвестных величин р1 и р2:

= pV ; p =

; p

= pV

; p

;

L − h + 2l

L − h − 2l

+ ρgh;

L − h − 2l = L − h + 2l + p(L − h);

L − h +

L – h – 2l

(L − h)2 − 4l2

2ρgh

p = ρgh

;

4l(L − h)

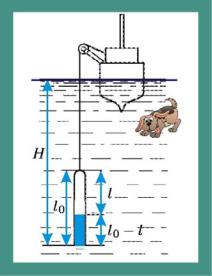
164. Ранее, до эпохи эхолотов, глубину

водоёмов измеряли верёвкой с навязанными

узлами и посредствам длинной с одним от-

крытым торцом стеклянной трубки, внутрен-

няя поверхность которой покрывалась рас-

творимой в воде краской. На какую глубину H,

была погружена трубка, если длина окрашен-

ной части трубки оказалась равной l.

Решение

1. Давление и объём воздуха в трубке до

её погружения:

{p0; V0 = sl0 ;}

2. Если нижний торец трубки находится на

глубине H:

Рис. 164. Измеритель глубины

{ p = p0 + ρg(H − l0 + l);

V = sl};

2. Считая температуру воздуха при погружении неизменной, получим:

p0V0 = pV; p0l0

= h[p0

+ ρg(H − l0 + l)];

H =

(p0 + ρgl)(l0 − l)

;

ρgl

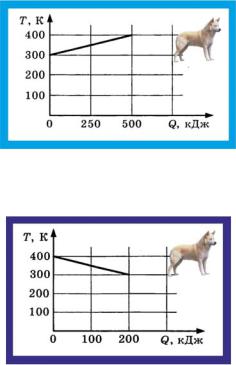
Два сосуда соединены тонкой трубкой краном

3. Термодинамика

165. Задан график зависимости температуры твёрдого тела от полученного им количества тепла. Масса тела m = 8 кг. Какова удельная теплоёмкость вещества этого тела?

Решение		Q
Q = cm T; c =			;
					m T

Q =	5 105		Дж	Рис. 165. Удельная теплоёмкость
	= 625				;
			8(400 −300)	кг К

166. Задан график зависимости температуры твёрдого тела от отданного им количества теплоты. Масса тела m = 4 кг. Какова удельная теплоёмкость вещества этого тела?

Решение

Q = cm T; c =		Q	;
		m T		Рис. 166. Удельная теплоёмкость

2 105	Дж
		Q =
= 500			;
	4(400 −300)			кг К

167.В кастрюлю, где находится вода объёмом V1 = 2 л при температуре t1

=25 0С, долили V2 = 3 л кипятка. Какая температура воды установится после полного смешения.

Решение

сρV2 (T2 −Θ)= cρV1(Θ−T1 ); V2T2 −V2Θ = V1Θ−V1T1;

Θ =	V1T1 + V2T2	=	2 298 +3 373	= 343K (70 0C);
	V + V		5

1	2

168. Удельная теплоёмкость воды равна с = 4200 Дж/кг К. Для измерения температуры воды массой m = 10 г используют термометр, который показывал температуру воздуха в помещении t1 = 20 0С, а после погружения в воду стал показывать t2 = 41 0С. Определить действительную температуру воды, если теплоёмкость термометра С = 2 Дж/К.

Решение

сm(T2 −Θ)= C(Θ−T1 ); cmT2 −cmΘ = CΘ−CT1;

Θ =	cmT2 +CT1	=	4200 10−2	314 +2 293	313K (40 0C);
	cm +C		42	+ 2

67

Два сосуда соединены тонкой трубкой краном

169. В фарфоровую чашку массой m1 = 0,1кг при температуре Т1 = 293 К влили m2 = 0,2 кг кипятка с Т2 = 373 К. Окончательная температура оказалась равной Θ = 366 К. Удельная теплоёмкость воды с2 = 4200 Дж/кг К. Определить удельную теплоёмкость фарфора.

Решение

m1c1(Θ−T1 )= m2c2 (T2 −Θ); m1c1 T1 = m2c2 T2 ;

c =	m2c2	T2	=	0,2 4200 7	= 805,5	Дж	;

1	m1	T1	0,1 73		кг К

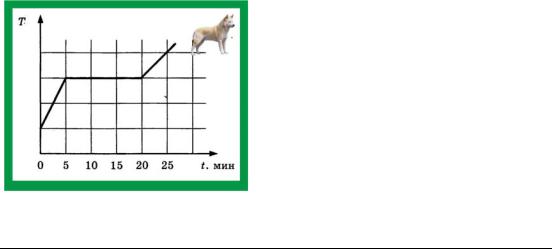
170. В печь поместили некоторое ко-
личество алюминия. Задана диаграмма
изменения		температуры алюминия от
времени. Нагреватель печи обеспечивает
передачу алюминию энергию в количест-
ве Ω = 2 кДж/мин. Какое количество теп-
лоты потребовало плавление алюминия?
Решение
1. Время плавления алюминия:
Рис. 170. Плавление алюминия			τПл =15 мин;

2. Количество тепла, полученного алюминием:

Q = Ωτ = 30 кДж ;

171. Сосуд, содержащий некоторое количество азота при нормальных условиях, движется со скоростью v = 100 м/с. Какой будет максимальная температура азота при внезапной остановке сосуда? Удельная теплоёмкость азота с

= 745 Дж/(кг К).

Решение

1. В момент остановки все молекулы азота будут иметь скорость сосуда и вся запасённая ими кинетическая энергия перейдёт в тепло:

mv2	= cm T;	T =	v2	=	104	6,7K;
2			2c		2 745

Tmax = T0 +	T = 273 + 6,7 = 279,7K;

172. На сколько градусов температура воды у основания водопада высотой h = 20 м больше, чем у его вершины? Полагать, что вся механическая энергия воды трансформируется в тепло. Удельная теплоёмкость воды с = 4200 Дж/(кг К).

Решение		10 20
mgh = cm T; T = gh	=		4,76 10−2 K;
		4200
c

173. Свинцовый шар, падая с некоторой высоты, после удара о землю нагрелся на Т = 4,5.К. Удельная теплоёмкость свинца с = 130 Дж/(кг К). Считая, что при ударе на нагрев пошла половина механической энергии, определить скорость шара перед ударом.

Решение
mv2	= cm T;	v = 2 c T = 2 130 4,5 48,37	м	;
4			с

174. С какой наименьшей высоты должны падать дождевые капли, чтобы при ударе о землю от них не осталось бы и «мокрого места»? В момент падения капель на землю их температура Т1 = 293 К, удельная теплоёмкость воды с = 4200 Дж/(кг К), удельная теплота парообразования r = 2,26 МДж/кг. Сопротивление воздуха отсутствует, ускорение свободного падения неизменно.

Решение
mgh = Qнагр + Qисп = сm T + mr;						T = 373 – 293 = 80K;
hmin =	c T	+ r	=	4200	80 + 2,26	106
	g	10		259,6км;

175. Какое количество дров потребуется, чтобы вскипятить m = 50 кг воды, имеющей температуру Т1 = 283 К, если КПД нагревателя η = 0,25, удельная теплота сгорания дров q = 10 МДж/кг.

Решение		4200 5 90
ηqm	x		= cm T;	m	x	= cm T	=	7,56кг;
ηq		0,25 107

176. Какое количество каменного угля необходимо для нагревания от Т1 = 283 К до Т2 = 323 К кирпичной печи массой m = 1200 кг, если КПД печи η = 0,3? Удельная теплоёмкость кирпича с = 750 Дж/(кг К), удельная теплота сгорания каменного угля q = 30 МДж/кг.

Решение			1200 (323 − 283)
ηqmx = cm T;	mx =	cm T		=	750	4кг;
		ηq	8
0,3 3 10

177.В электрический кофейник налили V = 0,16 л воды при температуре Т1

=30 0С и включили нагреватель. Через какое время после включения выкипит

вся вода, если мощность нагревателя N = 1 кВт, КПД нагревателя η = 0,8. Удельная теплоёмкость воды с = 4200 Дж/(кг К), удельная теплота парообразования воды λ = 2256 кДж/К.

Решение

ηNτ = cm T + λm; τ =	m(c	T	+ λ)	=	0,16(4200 70	+ 2,256 106 )	510c;
	ηN	0,8	103

178. Идеальный одноатомный газ переводят из первого состояния с р1 = 220 кПа, V1 = 1 10 − 3 м3 во второе состояние с р2 = 40 кПа, V2 = 2 10 − 3 м3. Определить работу, совершаемую газом.

Решение
A =	p + p	2 (V	− V )=	(220 + 40)103	1 10	−	3	=130Дж.
	1

2	2	1	2

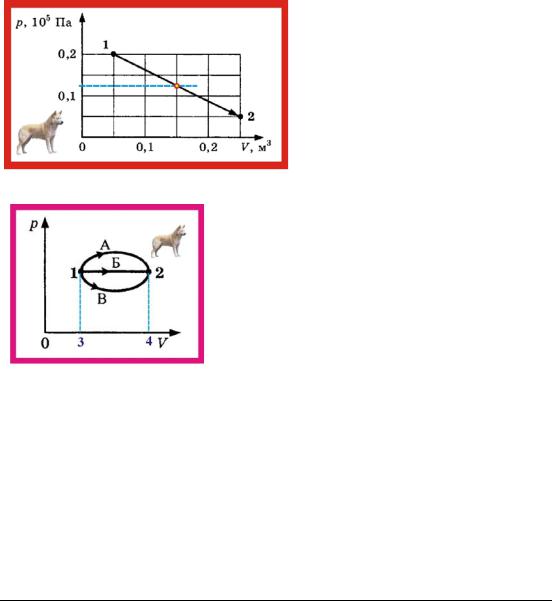
Два сосуда соединены тонкой трубкой краном

179. Какую работу совершил одноатомный газ в процессе, заданном в pV − координатах?

Решение

p1 + p2

(V − V );

1→2

2 1

2 104 + 5 103

2 = 25кДж ;

1→2

Рис. 179. Работа газа

180. В каком из заданных процессов при

переводе газа из состояния 1 в состояние 2

будет совершена наибольшая работа?

Решение

∫

< p > dV;

1→2

V = V2 − V1 = const;

Рис. 180. Сравнение работ

< p >A >< p >Б>< p >B;

A1→2(A) > A1→2(Б) > A1→2(B);

181. Одноатомный идеальный газ в количестве ν = 4 моль поглощает Q = 3

кДж теплоты, при этом его температура повышается на

Т = 20 К. Какая рабо-

та совершается газом в этом процессе?

Решение

Q = A + U = A +

νR T; A = Q −

νR T;

A3 103 − 32 4 8,3 20 2 кДж;

182.Один моль инертного газа сжали, совершив работу А = 600 Дж, в результате чего температура газа повысилась на Т = 40 К. Какое количество теплоты отдал газ?

i	Решение	3
	Q = A + U = A +		νR	T = 600 +	1 8,31 40 1,1 кДж;
2
	2

183. Тепловая машина имеет КПД η = 0,25. Средняя мощность передачи теплоты холодильнику в ходе её работы составляет NХ = 3 кВт. Какое количество теплоты получает машина от нагревателя в течение τ = 10 с?

Решение

η =1-

=1−

;

QH =

3 103 10

= 40 кДж;

− η

0,75

Источник