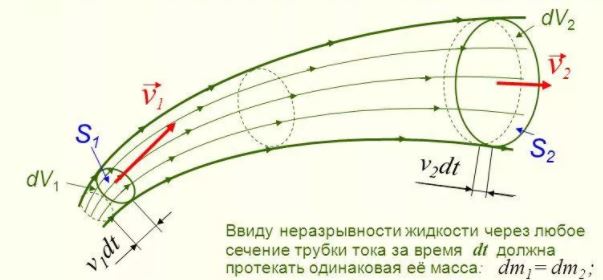
Движение жидкостей и газов в сосудах
Гидродинамика – раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа.
Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.
Идеальная среда
Гидродинамика изучает поведение идеальной жидкости – воображаемой среды без вязкости, сил трения и теплопроводности. Касательные напряжения равны нулю. Её можно представить, как систему небольших упругих шаров с пренебрежимо малым объёмом, не прилипающих друг к другу. Они часто сталкиваются друг с другом. Поэтому каждый шар переносит при движении массу, импульс, момент импульса, энергию.
Ламинарное и турбулентное движения жидкости
Экспериментально установлено, что в природе существуют два различных вида движения потока – ламинарное (слоистое, упорядоченное), при котором отдельные слои жидкости скользят друг относительно друга, и турбулентное (неупорядоченное), когда частицы жидкости движутся по сложным, все время изменяющимся траекториям.
Вследствие этого затрата энергии на турбулентное движение потока больше, чем на ламинарное.
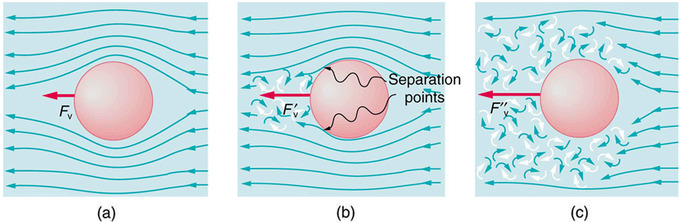
Турбулентность – название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средний значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов. Происходит их нелинейное вихревое взаимодействие и распространение в пространстве и времени.
Турбулентность может возникать и при нарушении сплошности среды, например, при кавитации (кипении). При опрокидывании и разрушении волны прибоя возникает многофазная смесь воды, воздуха, пены. Мгновенные параметры среды становятся хаотичными.
Ламинарное течение
Отличие ламинарного течения от турбулентного состоит в характере и направлении водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости.
Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости – потоком. Графически движение жидкостей изображается с помощью линий тока. Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.
Трубка тока – трубчатая поверхность, ограниченная линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.
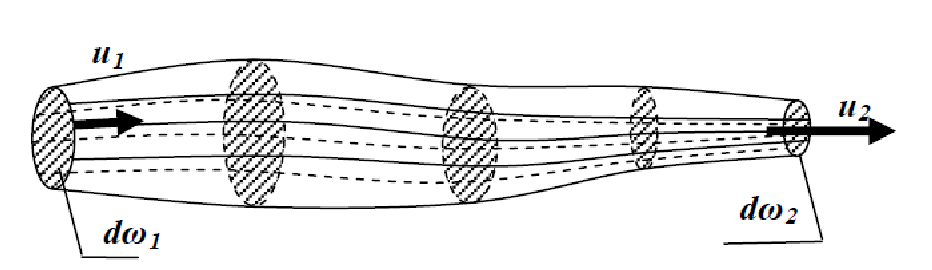
Для случая установившегося движения элементарной струйке придаются следующие свойства:
- форма элементарной струйки остается неизменной с течением времени;
- через стенки элементарной струйки движение жидкости не происходит (обмена энергией жидкости между элементарными струйками нет);
- вследствие малости поперечного сечения элементарной струйки скорость и гидродинамическое давление во всех точках ее поперечного сечения одинаковы.
Уравнение неразрывности жидкости
В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то за время Δt через сечение S проходит объем жидкости SvΔt; следовательно, за 1 с через S1 пройдет объем жидкости S1v1, где v1- скорость течения жидкости в месте сечения S1. Через сечение S2 за 1 с пройдет объем жидкости S2v2, где v2- скорость течения жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ = const), то через сечение S2пройдет такой же объем жидкости, как и через сечение S1, т. е.
S1v1 = S2v2 = const
Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.
Уравнение Бернулли
При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии.
Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах. У идеальной жидкости трение полностью отсутствует.
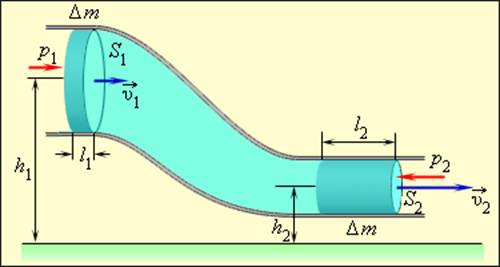
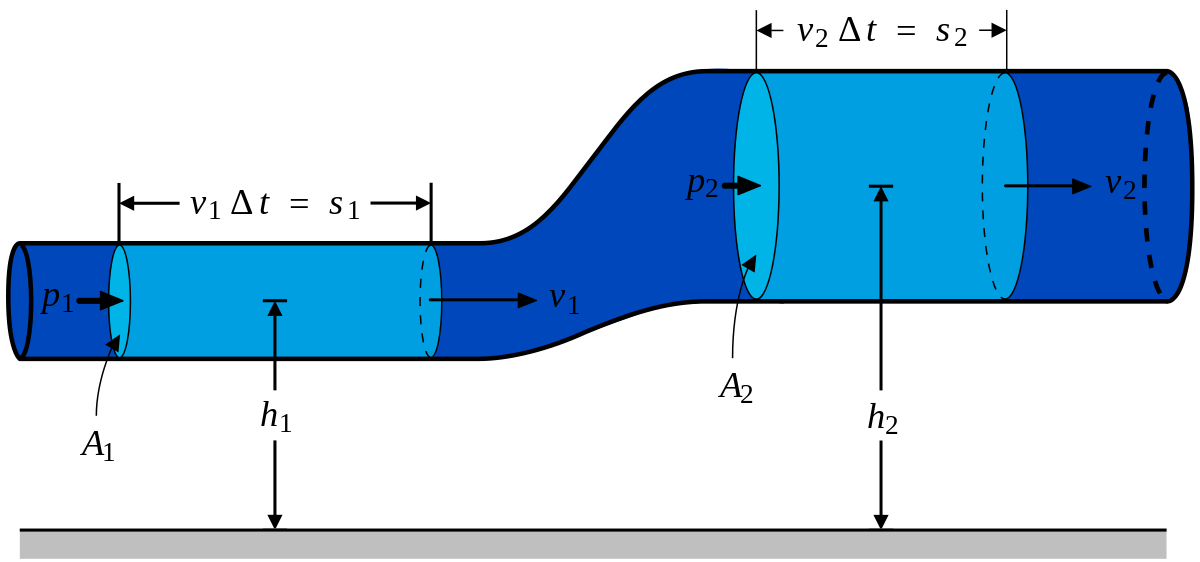
Выделим в стационарно текущей несжимаемой идеальной жидкости трубку тока, ограниченную сечениями S1 и S2, по которой жидкость течет слева направо. Пусть в месте сечения S1 скорость течения v1 давление р1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость течения v2, давление р2, высота сечения h2. За малый промежуток времени Δt жидкость перемещается от сечения S1 к сечениюS’1, от S2 к S’2.
Согласно закону сохранения энергии, изменение полной энергии Е2 – Е1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы т жидкости, где
– полные энергии жидкости массой т в местах сечений S1 и S2 соответственно.
С другой стороны, А – это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S1 и S2, за рассматриваемый малый промежуток времени Δt:
Тогда
или
где р – статическое давление (давление жидкости на поверхность обтекаемого ею тела),
ρv2/2 – динамическое давление.
Следствия:
1. Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше.
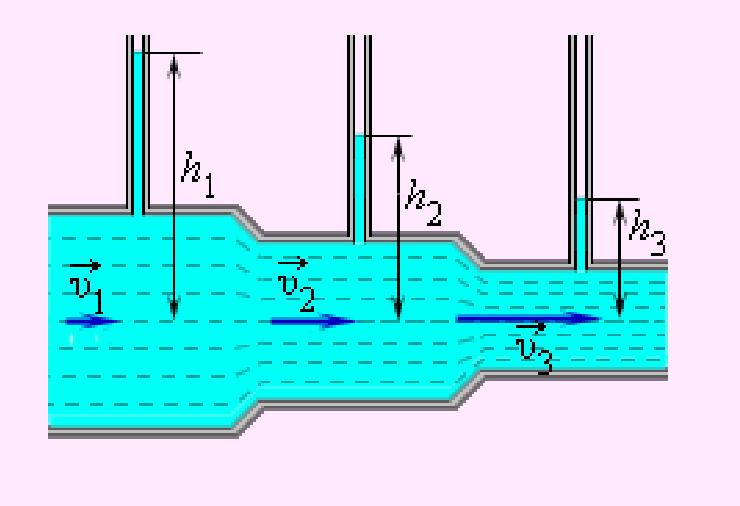
Это можно продемонстрировать, установив вдоль трубы ряд манометров. В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.
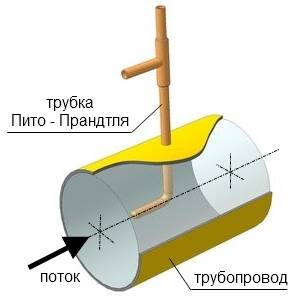
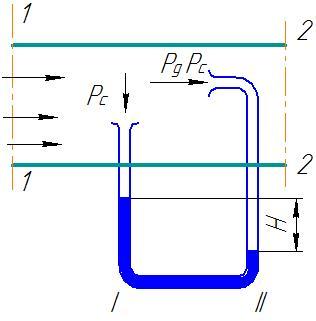
2. Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито – Прандтля. Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р0), с помощью другой – статическое (р).Манометром измеряется разность давлений:
p0 – p = ρ0gh
где ρ – плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:
p0 – p = ρv2/2
3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса. Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. = 133,32 Па).
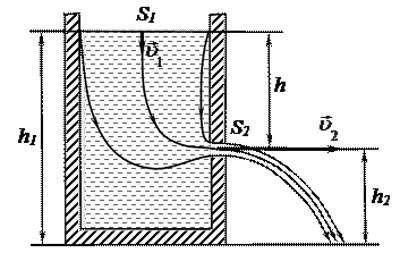
4. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие.
Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h2 выхода ее из отверстия). Напишем для них уравнение Бернулли:
Так как давления р1 и р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p1 = p2, то уравнение будет иметь вид
Из уравнения неразрывности следует, что v2/v1 = S1/S2, где S1 и S2 – площади поперечных сечений сосуда и отверстия. Если S1>>S2, то членом v21/2 можно пренебречь и
Это выражение получило название формулы Торричелли.

Источник
10 класс
Движение жидкостей и газов
Цель урока: дать учащимся некоторые сведения об элементах гидроаэродинамики, рассмотреть уравнение Бернулли, показать его практическое применение.
Тип урока: урок изучения нового материала.
Ход урока:
Актуализация знаний учащихся.
Повторение курса гидростатики, изученного в 7 классе.
а) закон Паскаля; гидростатическое давление.
б) гидростатический парадокс; сообщающиеся сосуды.
2. Изучение новой темы:
а) вывод уравнения Бернулли.
Описать движение жидкости и газа гораздо труднее, чем решить задачи гидростатики. Хотя гидроаэродинамика основана на трех хорошо знакомых в механике законах сохранения массы, импульса и энергии, их формулировка здесь выглядит немного сложнее. Например, определение закона сохранения массы обычно выглядит так: масса системы тел остается неизменной. Для жидкости, текущей в трубе, этот закон используется в форме (называемой уравнением неразрывности):
VS=const
Здесь -V скорость жидкости, S-площадь сечения трубы, по которой течет жидкость. Сформулировать этот закон можно так: сколько вливается жидкости в трубу, столько должно и выливаться, если условия течения не изменяются. Скорость в узких участках трубы должна быть выше, чем в широких. Одно из важнейших уравнений гидромеханики было получено в 1738 году швейцарским ученым Даниилом Бернулли. Ему впервые удалось описать движение несжимаемой идеальной жидкости. Уравнение Бернулли выражает закон сохранения энергии и условие неразрывности течения идеальной жидкости. За время t элемент массой m = рS1V1 = pS2V2спустился с уровня h на уровень h, а его скорость увеличилась с V1 до V2. Приращение кинетической энергии элемента жидкости равно
Ек = m(V22/2 – V12/2) = 1/2рt(S2V23 – S1V13)
Изменение потенциальной энергии этого же элемента составляет
Е = mg(h2 – h1) = pgt(S2V2h2 – S1V1h1)
Работа сил давления, совершенная над элементом жидкости при его перемещении, равна
А = P1S1V1t – P2V2S2t
Запишем закон сохранения энергии:
А = Ек + Еп
После подстановки и сокращений получим:
P1 + pV12/2 + pgh1 = P2 + pV22 + pgh2
или
Р + рV2/2 + pgh = const
В этом уравнении все слагаемые имеют размерность давления и соответственно называются: Р-статическое давление, pV2/2 -динамическое давление, pgh- весовое давление. При отсутствии скорости уравнение Бернулли превращается в гидростатическую формулу. Если труба устроена так, что давление в ней остается постоянным, уравнение Бернулли для жидкости просто совпадает с законом сохранения энергии для материальной точки. Если же труба устроена так, что можно не учитывать изменение высоты h (в силу малой плотности вещества или малого изменения этой высоты), то результат получится неожиданным: скорость в узких участках трубы растет, – значит там должно падать давление. Максимальное давление в трубах устанавливается именно там, где труба имеет наибольшее сечение; здесь ее материал может не выдержать и разорваться. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, – это тоже приведет к разрушению материала трубы.
б) Уравнение Бернулли просто объясняет множество явлений, происходящих в жидкости и газе.
1) Например, крыло самолета, которое обтекает равномерный поток воздуха. Даже при отсутствии у крыла угла атаки, т. е. наклона по направлению к набегающему потоку, существует подъемная сила, направленная вверх. Именно из-за такой формы крыла, в соответствии с уравнением неразрывности получается, что скорость воздуха под крылом меньше, чем над ним. Это означает, что давление снизу крыла больше, чем давление сверху. Разность давлений и создает подъемную силу.
2) Капитаны морских и речных судов прекрасно знакомы с коварным проявлением уравнения Бернулли. Если два корабля идут параллельным курсом слишком близко один к другому, возникает гидродинамическая сила, толкающая их друг к другу, в результате чего может произойти кораблекрушение. Формула Бернулли позволяет понять, почему возникает эта сила: относительная скорость воды между судами будет больше, чем снаружи, давление воды на корабли в пространстве между ними окажется ниже, чем извне. Перепад давлений по разные стороны кораблей создает силу, толкающую их друг к другу.
3)Закон Бернулли позволяет измерять скорость движения жидкости или газа с помощью манометра – прибора для измерения давления.
3. Закрепление темы проводится в виде решения качественных и расчетных задач.
1) Почему, спускаясь на лодке по реке, плывут посредине реки, а поднимаясь, стараются держаться берега?
Это связано с тем, что скорость течения в разных точках различна: скорость течения реки посредине реки больше, чем у берегов. Поэтому при спуске плывут посредине реки, что облегчает спуск, т. к. к скорости лодки прибавляется скорость течения реки. При подъеме стараются держаться берега, чтобы течение реки не сильно сносило лодку, т.к. скорость движения лодки при этом уменьшается на величину скорости течения реки.
2) Почему сильный ветер вздымает высоко над землей сухие листья?
Благодаря большой скорости воздушного потока давление воздуха на поверхности этих предметов становится меньше атмосферного, т. к. чем больше скорость воздуха, тем меньше его давление. Под листьями давление атмосферное. Вследствие разности давлений возникает подъемная сила, которая и поднимает листья над землей.
3) Если вблизи от нас проходит скорый поезд, то мы чувствуем, как нас притягивает к нему. Почему это происходит?
4) Задача: В полете давление воздуха под крылом самолета 97,8 кН/м2, а над крылом 96,8 кН/м2. Площадь крыла 20 м2. Определить подъемную силу.
Решение:
F = PS, где P = P2 – P1, тогда F = (P2 – P1)S, F =20.103 H
Ответ: 20кН
10 класс
Практическая работа №3: Компьютерное моделирование движения точки
Цель: ввести понятие механического движения, ознакомить учеников с основными понятиями, которые характеризуют механическое движение, дать представление об относительности механического движения.
ХОД УРОКА
I. Организационный этап
II. Актуализация опорных знаний и умений
Приведите примеры тел, которые двигаются, и неподвижных тел.
Чем тела, которые двигаются, отличаются от тел неподвижных?
III. Изучение нового материала
План изучения новой темы
Определение механики.
Механическое движение.
Виды движения.
Основная задача механики.
Относительность механического движения.
Тело отсчета.
Системы координат.
Система отсчета.
Векторные и скалярные величины.
Траектория.
Путь.
Перемещение.
Материальная точка.
Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.
Механическое движение – это изменение в пространстве с течением времени взаимного расположения тел или их частей.
Основная задача механики – определить положение тела в любой момент времени.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчёта. Оно считается неподвижным (для данной задачи).
Положение тела в пространстве описывается с помощью системы координат. Реальное пространство трёхмерно, и положение материальной точки в любой момент времени полностью определяется тремя числами – её координатами в выбранной системе отсчета.
Как правило, используют прямоугольную, или декартову, систему координат1. Для описания движения точки, кроме тела отсчёта и системы координат, необходимо ещё иметь часы – устройство, с помощью которого можно измерять различные отрезки времени.
Тело отсчёта, система координат и связанные с ней часы образуют систему отсчета.
Рисунок 1
OX – ось абсцисс, OY – ось ординат, OZ – ось аппликат.
Рисунок 2
Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки – абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки.
Под воздействием тел друг на друга тела могут деформироваться, т. е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель – абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным.
Физическая величина – это характеристика, которая является общей для нескольких материальных объектов или явлений в качественном отношении, но может принимать индивидуальные значения для каждого из них.
Измерить физическую величину – значит сравнить её с однородной величиной, принятой за единицу.
Примеры физических величин – путь, время, масса, плотность, сила, температура, давление, напряжение, освещённость и т.п.
Физические величины бывают скалярные и векторные. Скалярные физические величины характеризуются только численным значением, тогда как векторные определяются и числом (модулем), и направлением. Скалярными физическими величинами являются время, температура, масса, векторными – скорость, ускорение, сила.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Радиус-вектор точки М – направленный отрезок прямой, соединяющий начало отсчёта О с точкой М. (Рис.3)
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t) и радиус-вектора . – радиус-вектор положения точки в начальный момент времени.
IV. Закрепления новых знаний и умений
Человек едет в трамвае. Назовите тела, относительно которых человек находится в состоянии покоя, а относительно которых – двигается.
Зависит ли форма траектории от выбора тела отсчета? Проиллюстрируйте ответ примерами.
Приведите примеры ситуаций, в которых тело можно считать материальной точкой.
Решение задач
Спортсмен проплывает водную дорожку в бассейне 2 раза. Найдите путь и перемещение спортсмена, если длина дорожки в бассейне равна 50 м.
Эскалатор поднимает неподвижного пассажира за 1 минуту. Если эскалатор неподвижный, то пассажир поднимается за 3 минуты. За какое время пассажир поднимается по эскалатору, который двигается вверх?
Подведение итогов урока
Домашнее задание
11 класс
Практическая работа решение экспериментальных задач
Цели урока:
Образовательные: обобщение и систематизация знаний по теме, проверка знаний, умений, навыков. В целях повышения интереса к теме работу вести с помощью опорных конспектов.
Воспитательные: воспитание мировоззренческого понятия (причинно-следственных связей в окружающем мире), развитие у школьников коммуникативной культуры.
Развивающие: развитие самостоятельности мышления и интеллекта, умение формулировать выводы по изученному материалу, развитие логического мышления, развитие грамотной устной речи, содержащей физическую терминологию.
ХОД УРОКА
Электромагнитные колебания – это периодические и почти периодические изменения заряда, силы тока и напряжения.
Колебательный контур – цепь, состоящая из соединительных проводов, катушки индуктивности и конденсатора.
Свободные колебания – это колебания, происходящие в системе благодаря начальному запасу энергии с частотой, определяемой параметрами самой системы: L, C.
Скорость распространения электромагнитных колебаний равна скорости света: С = 3 . 108(м/с)
Основные характеристики колебаний
Амплитуда (силы тока, заряда, напряжения) – максимальное значение (силы тока, заряда, напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда, напряжения) – i, q, u
Схема колебательного контура
Электромагнитные колебания представляют периодический переход электрической энергии конденсатора в магнитную энергию катушки и наоборот согласно закону сохранения энергии.
Задача №1
Колебательный контур содержит конденсатор емкостью 800 пФ и катушку индуктивности индуктивностью 2 мкГн. Каков период собственных колебаний контура?
Задача № 2
Колебательный контур состоит из конденсатора емкостью С и катушки индуктивности индуктивностью L. Как изменится период свободных электромагнитных колебаний в этом контуре, если электроемкость конденсатора и индуктивность катушки увеличить в 3р.
Задача № 3
Амплитуда силы тока при свободных колебаниях в колебательном контуре 100 мА. Какова амплитуда напряжения на конденсаторе колебательного контура, если емкость этого конденсатора 1 мкФ, а индуктивность катушки 1 Гн? Активным сопротивлением пренебречь.
11 класс
Практическая работа Компьютерное моделирование электромагнитных волн и изучение их свойств.
Цель:
Перечислите свойства электромагнитных волн.
Перечислите электромагнитные волны.
боты в ПП Matcad) 10
В) Запишите уравнения и зарисуйте графики в тетрадях
Г) Сделайте выводы
Подведение итогов урока
Что сегодня нового вы узнали на уроке?
Какие возможности дает компьютерное моделирование
Выставление оценок
Домашнее задание: повторение тем электром.волны
Алау
100,7 МГц
Европа +
100.2 МГц
Казахское радио
105,4 МГц
КН
101.5 МГц
Ностальжи
73.85 МГц
НС
107,00 МГц
Источник