Движение жидкостей в сосудах
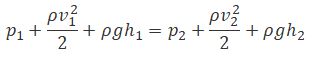
В зависимости от характера действующих массовых сил поверхность равного давления в жидкости, как и свободная поверхность, может принимать различную форму. Ниже рассматриваются некоторые случаи равновесия жидкости в движущихся сосудах.
1. Жидкость находится в сосуде, который движется в горизонтальном направлении с постоянным ускорением ±а (знак плюс соответствует ускорению сосуда, знак минус – замедлению ) (см. рисунок).

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и инерции. Поверхность равного давления является наклонной плоскостью. Давление в любой точке жидкости определяется по формуле
p = p0 + ρ·(g·z ± a·x),
Для свободной поверхности жидкости, когда р=p0, уравнение принимает вид:
g·z = ± a·x
или
z/x = tg α = ± a/g,
где α – угол наклона свободной поверхности жидкости к горизонту.
Последнее приведенное выше выражение позволяет определять (при условии, чтобы жидкость не переливалась через задний борт сосуда длиной l) высоту борта h при заданном значении а или предельное ускорение а при заданном значении h.
Если сосуд движется равномерно (а = 0), уравнение приводим к виду:
p = p0 + ρ·g·z = p0·γ
В этом случае поверхность равного давления представляет горизонтальную плоскость.
2. Жидкость находится в открытом цилиндрическом сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω.

В данном случае жидкость подвержена воздействию не только поверхностных сил, но также массовых сил тяжести и центробежной.
Поверхность равного давления представляет параболоид вращения. Распределение давления в жидкости по глубине определяется выражением:
p = p0 + γ·((ω2·r2)/(2·g) – z)
Для любой точки свободной поверхности жидкости, когда p = p0, уравнение принимает вид:
z = (ω2·r2)/(2·g) = u2/(2·g),
где окружная скорость u = ω·r (r – радиус вращения точки).
Высота параболоида вращения:
h = ω2·r20/(2·g),
где r0 – радиус цилиндрического сосуда.
Сила давления жидкости на дно сосуда:
P = γ·π·r20·h0 = γ·π·r20·(h1 + h/2),
где h0 – начальная глубина жидкости в сосуде до момента его вращения.
Давление на боковую стенку сосуда изменяется по линейному закону. Эпюра давления представляет прямоугольный треугольник ACD с высотой h1 + h и основанием γ·(h1 + h).
3. Жидкость находится в цилиндрическом сосуде, который вращается вокруг горизонтальной оси с постоянной угловой скоростью ω.
В данном случае жидкость также подвержена воздействию массовых сил тяжести и центробежной.
Поверхности равного давления представляют концентрически расположенные боковые поверхности цилиндров, оси которых горизонтальны и смещены относительно оси оу на величину эксцентриситета e = g/ω2 (см. рисунок а).

При большом числе оборотов сосуда влияние силы тяжести по сравнению с влиянием центробежной силы становится незначительным, и, следовательно, величиной эксцентриситета е можно пренебречь. Тогда поверхности равного давления становятся концентрическими цилиндрами, оси которых совпадают с осью сосуда (см. рисунок б).
Распределение давления по глубине жидкости определяется выражением:
p = p0 + γ·ω2·(r2 – r20)/(2·g)
где p и p0 – соответственно давления в точках цилиндрических поверхностей с радиусами r и r0.
Данное уравнение справедливо и тогда, когда сосуд радиусом r лишь частично заполнен жидкостью. Свободная поверхность жидкости в этом случае также будет цилиндрической с радиусом r0 и давлением во всех ее точках р0.
Как видно из последнего уравнения, закон распределения давления по радиусу является параболическим. Эпюра давления представленная на рисунке в. Такие приближенные решения могут применяться при любом положении оси вращения сосуда, однако при условии большого числа его оборотов.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Источник
Гидродинамика – раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа.
Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.
Идеальная среда
Гидродинамика изучает поведение идеальной жидкости – воображаемой среды без вязкости, сил трения и теплопроводности. Касательные напряжения равны нулю. Её можно представить, как систему небольших упругих шаров с пренебрежимо малым объёмом, не прилипающих друг к другу. Они часто сталкиваются друг с другом. Поэтому каждый шар переносит при движении массу, импульс, момент импульса, энергию.
Ламинарное и турбулентное движения жидкости
Экспериментально установлено, что в природе существуют два различных вида движения потока – ламинарное (слоистое, упорядоченное), при котором отдельные слои жидкости скользят друг относительно друга, и турбулентное (неупорядоченное), когда частицы жидкости движутся по сложным, все время изменяющимся траекториям.
Вследствие этого затрата энергии на турбулентное движение потока больше, чем на ламинарное.
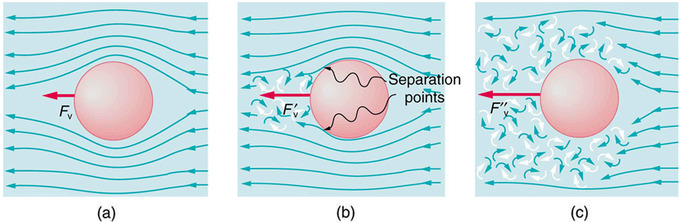
Турбулентность – название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средний значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов. Происходит их нелинейное вихревое взаимодействие и распространение в пространстве и времени.
Турбулентность может возникать и при нарушении сплошности среды, например, при кавитации (кипении). При опрокидывании и разрушении волны прибоя возникает многофазная смесь воды, воздуха, пены. Мгновенные параметры среды становятся хаотичными.
Ламинарное течение
Отличие ламинарного течения от турбулентного состоит в характере и направлении водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости.
Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.
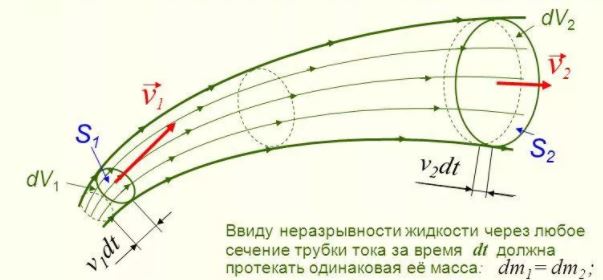
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости – потоком. Графически движение жидкостей изображается с помощью линий тока. Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.
Трубка тока – трубчатая поверхность, ограниченная линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.
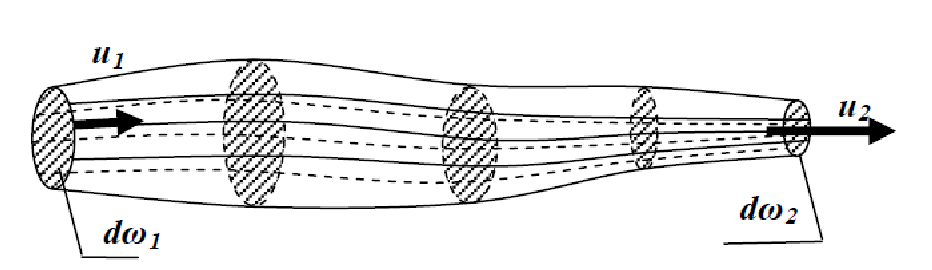
Для случая установившегося движения элементарной струйке придаются следующие свойства:
- форма элементарной струйки остается неизменной с течением времени;
- через стенки элементарной струйки движение жидкости не происходит (обмена энергией жидкости между элементарными струйками нет);
- вследствие малости поперечного сечения элементарной струйки скорость и гидродинамическое давление во всех точках ее поперечного сечения одинаковы.
Уравнение неразрывности жидкости
В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то за время Δt через сечение S проходит объем жидкости SvΔt; следовательно, за 1 с через S1 пройдет объем жидкости S1v1, где v1- скорость течения жидкости в месте сечения S1. Через сечение S2 за 1 с пройдет объем жидкости S2v2, где v2- скорость течения жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ = const), то через сечение S2пройдет такой же объем жидкости, как и через сечение S1, т. е.
S1v1 = S2v2 = const
Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.
Уравнение Бернулли
При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии.
Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.
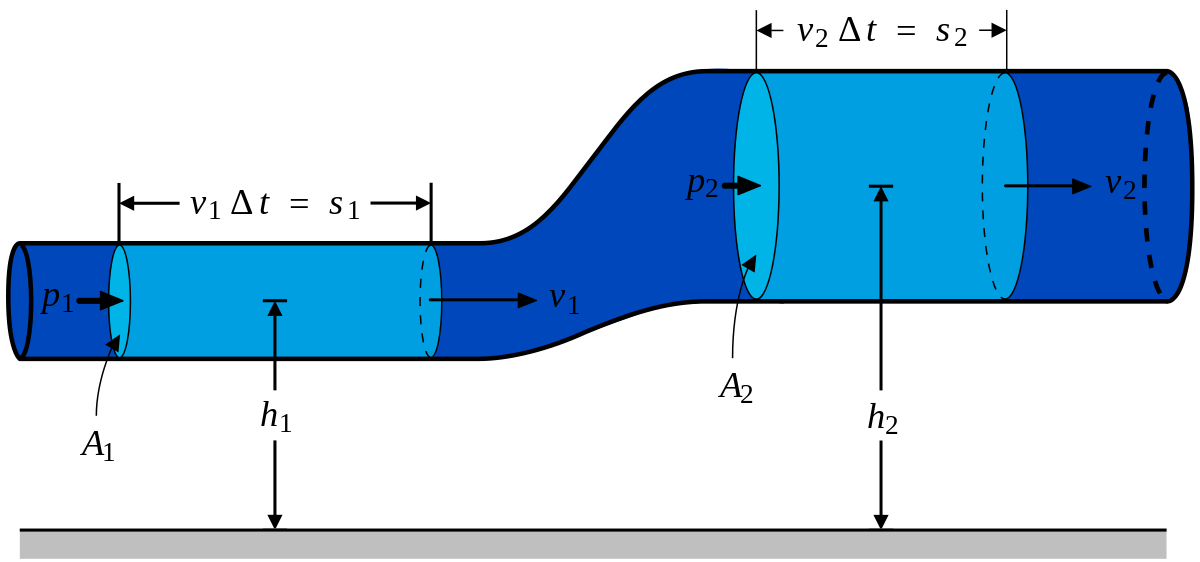
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах. У идеальной жидкости трение полностью отсутствует.
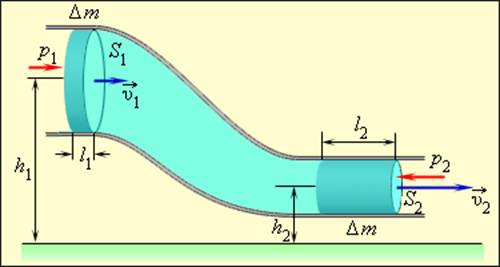
Выделим в стационарно текущей несжимаемой идеальной жидкости трубку тока, ограниченную сечениями S1 и S2, по которой жидкость течет слева направо. Пусть в месте сечения S1 скорость течения v1 давление р1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость течения v2, давление р2, высота сечения h2. За малый промежуток времени Δt жидкость перемещается от сечения S1 к сечениюS’1, от S2 к S’2.
Согласно закону сохранения энергии, изменение полной энергии Е2 – Е1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы т жидкости, где
– полные энергии жидкости массой т в местах сечений S1 и S2 соответственно.
С другой стороны, А – это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S1 и S2, за рассматриваемый малый промежуток времени Δt:
Тогда
или
где р – статическое давление (давление жидкости на поверхность обтекаемого ею тела),
ρv2/2 – динамическое давление.
Следствия:
1. Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше.
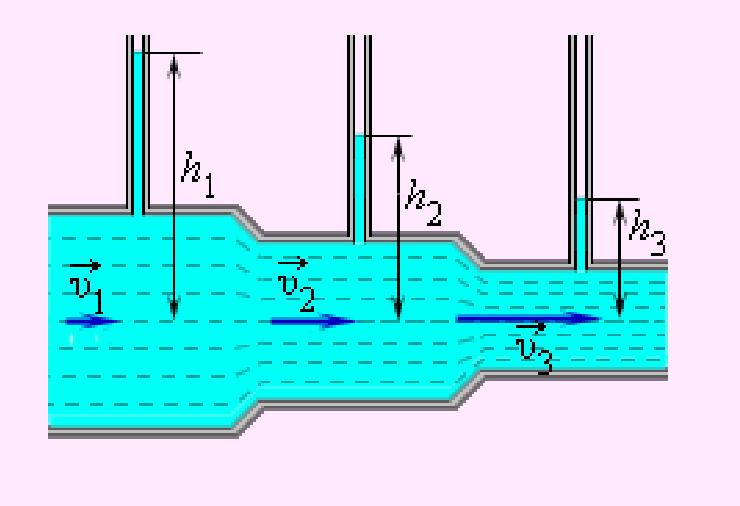
Это можно продемонстрировать, установив вдоль трубы ряд манометров. В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.
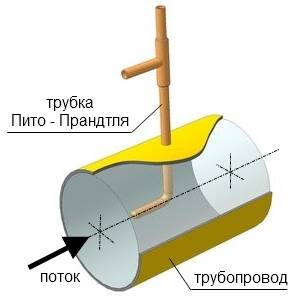
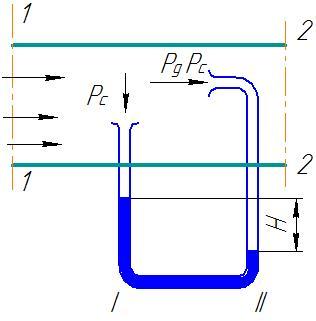
2. Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито – Прандтля. Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р0), с помощью другой – статическое (р).Манометром измеряется разность давлений:
p0 – p = ρ0gh
где ρ – плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:
p0 – p = ρv2/2
3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса. Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. = 133,32 Па).
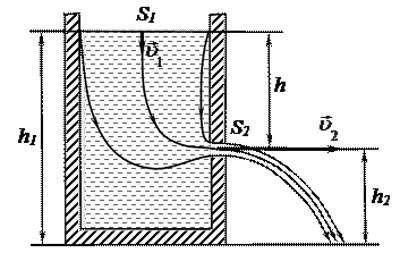
4. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие.
Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h2 выхода ее из отверстия). Напишем для них уравнение Бернулли:
Так как давления р1 и р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p1 = p2, то уравнение будет иметь вид
Из уравнения неразрывности следует, что v2/v1 = S1/S2, где S1 и S2 – площади поперечных сечений сосуда и отверстия. Если S1>>S2, то членом v21/2 можно пренебречь и
Это выражение получило название формулы Торричелли.
Источник
Мы поможем в написании ваших работ! Мы поможем в написании ваших работ! Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? | Принципы и уравнения, используемые для описания движения идеальных жидкостей в трубках, часто применяют для объяснения поведения крови в кровеносных сосудах. Однако кровеносные сосуды – не жёсткие трубки, а кровь – не идеальная жидкость, а двухфазная система (плазма и клетки), поэтому характеристики кровообращения отклоняются (иногда весьма заметно) от теоретически рассчитанных. · Ламинарный поток. Движение крови в кровеносных сосудах можно представить как ламинарное (т.е. обтекаемое, с параллельным течением слоёв). Слой, прилежащий к сосудистой стенке, практически неподвижен. Следующий слой движется с небольшой скоростью, в слоях ближе к центру сосуда скорость движения нарастает, а в центре потока максимальна. Ламинарное движение сохраняется до достижения некоторой критической скорости. Выше критической скорости ламинарный поток становится турбулентным (вихревым). Ламинарное движение бесшумно, турбулентное движение порождает звуки, при должной интенсивности слышимые стетофонендоскопом. · Турбулентный поток. Возникновение турбулентности зависит от скорости потока, диаметра сосуда и вязкости крови. Сужение артерии увеличивает скорость кровотока через место сужения, создаёт турбулентность и звуки ниже места сужения. Примеры шумов, воспринимаемых над стенкой артерии, – шумы над участком сужения артерии, вызванным атеросклеротической бляшкой, и тоны Короткова при измерении АД. При анемии наблюдают турбулентность в восходящей аорте вследствие снижения вязкости крови, отсюда и систолический шум. · Формула Пуазейля. Соотношение между током жидкости в длинной узкой трубке, вязкостью жидкости, радиусом трубки и сопротивлением определяется по формуле Пуазейля: , где R – сопротивление трубки, h – вязкость протекающей жидкости, L – длина трубки, r – радиус трубки. Так как сопротивление обратно пропорционально четвёртой степени радиуса, то в организме кровоток и сопротивление существенно меняются в зависимости от небольших изменений калибра сосудов. Например, кровоток через сосуды удваивается при увеличении их радиуса только на 19%. Когда радиус увеличивается в 2 раза, то сопротивление уменьшается на 6% от исходного уровня. Эти выкладки позволяют понять, почему органный кровоток столь эффективно регулируется минимальными изменениями просвета артериол и почему вариации диаметра артериол оказывают такой сильный эффект на системное АД. · Вязкость и сопротивление. Сопротивление кровотоку определяется не только радиусом кровеносных сосудов (сопротивление сосудов), но и вязкостью крови. Плазма примерно в 1,8 раза более вязкая, чем вода. Вязкость цельной крови в 3-4 раза выше вязкости воды. Следовательно, вязкость крови в значительной степени зависит от гематокрита, т.е. процентного содержания эритроцитов в крови. В крупных сосудах увеличение гематокрита вызывает ожидаемое повышение вязкости. Однако в сосудах с диаметром менее 100 мкм, т.е. артериолах, капиллярах и венулах изменения вязкости на единицу изменений гематокрита намного меньше, чем в больших сосудах. à Изменения гематокрита сказываются на периферическом сопротивлении, главным образом, крупных сосудов. Тяжёлая полицитемия (увеличение количества эритроцитов разной степени зрелости) повышает периферическое сопротивление, увеличивая работу сердца. При анемии периферическое сопротивление понижено, отчасти за счёт уменьшения вязкости. à В сосудах эритроциты стремятся расположиться в центре текущего потока крови. Следовательно, вдоль стенок сосудов движется кровь с низким гематокритом. Ответвления, отходящие от крупных сосудов под прямыми углами, могут получать непропорционально меньшее количество эритроцитов. Этот феномен, называемый скольжением плазмы, может объяснять тот факт, что гематокрит капиллярной крови постоянно на 25% ниже, чем в остальных частях тела. · Критическое давление закрытия просвета сосудов. В жёстких трубках соотношение между давлением и скоростью потока гомогенной жидкости линейное, в сосудах такой зависимости нет. Если давление в мелких сосудах уменьшается, то кровоток останавливается раньше, чем давление упадёт до нуля. Это касается прежде всего давления, продвигающего эритроциты через капилляры, диаметр которых меньше размеров эритроцитов. Ткани, окружающие сосуды, оказывают на них постоянное небольшое давление. При понижении внутрисосудистого давления ниже тканевого давления сосуды спадаются. Давление, при котором кровоток прекращается, называют критическим давлением закрытия. · Растяжимость и податливость сосудов. Все сосуды растяжимы. Это свойство играет важную роль в кровообращении. Так, растяжимость артерий способствует формированию непрерывного тока крови (перфузии) через систему мелких сосудов в тканях. Из всех сосудов наиболее растяжимы вены. Небольшое повышение венозного давления приводит к депонированию значительного количества крови, обеспечивая ёмкостную (аккумулирующую) функцию венозной системы. Растяжимость сосудов определяют как увеличение объёма в ответ на повышение давления, выраженное в миллиметрах ртутного столба. Если давление в 1 мм рт.ст. вызывает в кровеносном сосуде, содержащем 10 мл крови, увеличение этого объёма на 1 мл, то растяжимость будет составлять 0,1 на 1 мм рт.ст. (10% на 1 мм рт.ст.). à На практике важнее знать общее количество сосудов, способных резервировать кровь из кровообращения в ответ на каждый миллиметр ртутного столба повышенного давления, чем просто растяжимость отдельных сосудов. Такое понятие, характеризующее эластичность сосудистой стенки, называют податливостью. Чем выше податливость, тем больше растяжимость кровеносных сосудов. à Растяжимость и податливость различаются между собой. Сосуды, имеющие высокую растяжимость, но имеющие малый объём, могут иметь намного меньшую податливость, чем менее растяжимые сосуды, имеющие большой объём. Так, податливость вены в 24 раза больше, чем в соответствующей артерии, потому что она в 8 раз растяжимее и имеет в 3 раза больший объём. Единица измерения податливости – 1 мл/мм рт.ст. · Стресс-релаксация. В венозном сосудистом русле проявляется так называемый феномен стресс-релаксации, свойственный всем ГМК. Введённый внутривенно значительный объём крови вызывает немедленное эластическое растяжение вен, а ГМК после быстрой релаксации начинают медленно возвращаться к исходной длине. Стресс-релаксация, увеличивая податливость, служит механизмом для поддержания адекватного кровообращения при переливании больших объёмов крови. Этот же механизм работает и в обратном направлении, автоматически приспосабливая кровообращение к деятельности в условиях уменьшенного объёма крови после большой кровопотери. Важно учитывать, что в состоянии покоя более 60% ОЦК находится в венозной системе. При переливании крови менее 1% её объёма распределяется в артериальной системе (системе высокого давления), а вся остальная кровь распределяется в венозной системе, малом круге кровообращения, предсердиях и правом желудочке (системе низкого давления). |
Источник