Если в геометрическом сосуде объемом
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задание
8
#3045
Уровень задания: Равен ЕГЭ
Объем первого шара равен равен (54). Найдите объем второго шара, если его радиус в (3) раза меньше радиуса первого шара.
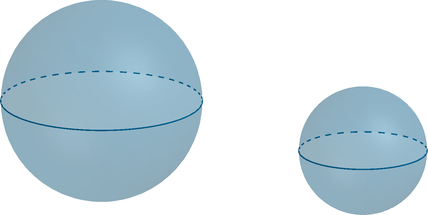
Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{54}{V_2}=dfrac{V_1}{V_2}=
dfrac{frac43 pi ,R_1^3}{frac43 pi
,R_2^3}=left(dfrac{R_1}{R_2}right)^3] Так как радиус второго шара в 3 раза меньше радиуса первого шара, то (R_1=3R_2), следовательно, [dfrac{54}{V_2}=left(dfrac{3R_2}{R_2}right)^3=27 quadRightarrowquad
V_2=dfrac{54}{27}=2.]
Ответ: 2
Задание
9
#3053
Уровень задания: Равен ЕГЭ
Сосуд имеет форму конуса и вмещает в себя 2700 мл жидкости. Определите, сколько мл жидкости налито в сосуд, если высота жидкости в 3 раза меньше высоты сосуда.
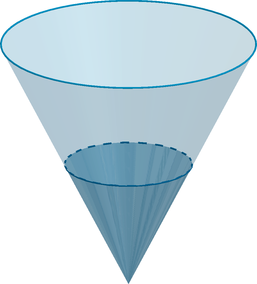
Пусть (O) – центр основания большего конуса, (Q) – меньшего, а (S) – их общая вершина. В одной плоскости проведем радиусы (OA) и (QB), как показано на рисунке:
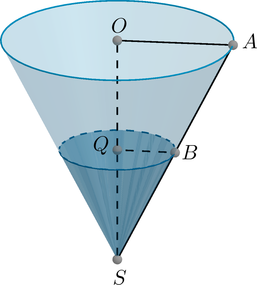
Тогда (QBparallel OA) и (triangle SQBsim triangle SOA). Следовательно, [dfrac{QB}{OA}=dfrac{QS}{OS}=dfrac13] Тогда объем налитой жидкости к объему всего сосуда относится как [dfrac{V_{small{text{ж}}}}{2700}=dfrac{V_{small{text{ж}}}}{V}=
dfrac{frac13cdot picdot QB^2cdot QS}{frac13cdot pi cdot
OA^2cdot OS}= left(dfrac{QB}{OA}right)^2cdot
dfrac{QS}{OS}=dfrac19cdot dfrac13=dfrac1{27}]
Следовательно объем жидкости равен [V_{small{text{ж}}}=dfrac1{27}V=100]
Ответ: 100
Задание
10
#3054
Уровень задания: Равен ЕГЭ
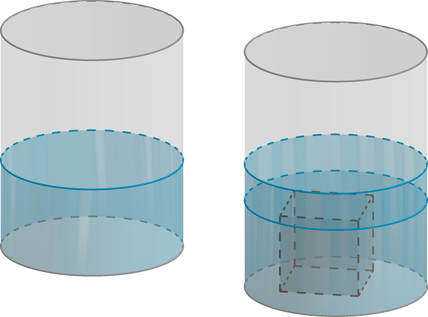
В сосуд цилиндрической формы, объем которого 2400 см(^3), налили жидкость, заполнив сосуд на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических сантиметрах.

Объем цилиндра вычисляется по формуле (V=pi R^2H), где (R) – радиус основания, (H) – высота. Таким образом, во сколько раз увеличивается/уменьшается высота цилиндра, во столько же раз увеличивается/уменьшается объем цилиндра.
Следовательно, если жидкость заполнила сосуд лишь на треть, то есть высота жидкости в 3 раза меньше высоты сосуда, то и объем жидкости в 3 раза меньше объема сосуда, следовательно, объем жидкости равен (2400:3=800) см(^3).
Так как после погружения в жидкость предмета уровень повысился на четверть, то и занимаемый в сосуде объем повысился на четверть.
Закон Архимеда гласит, что объем вытесненной жидкости равен объему погруженного в нее предмета. Следовательно, объем предмета равен четверти объема жидкости, то есть (800:4=200) см(^3).
Ответ: 200
Задание
11
#3042
Уровень задания: Равен ЕГЭ
Радиус первого шара равен (6), а радиус второго шара равен (2). Во сколько раз объем первого шара больше объема второго шара?

Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{V_1}{V_2}=dfrac{frac43 pi cdot 6^3}{frac43 pi cdot 2^3}=
left(dfrac62right)^3=27.] Следовательно, объем первого шара в 27 раз больше объема второго шара.
Ответ: 27
Задание
12
#3050
Уровень задания: Равен ЕГЭ
Объем первого цилиндра равен (16), причем известно, что его радиус в 7 раз меньше радиуса второго цилиндра, а высота второго цилиндра в 8 раз меньше высоты первого. Найдите объем второго цилиндра.
Объем цилиндра с высотой (H) и радиусом основания (R) ищется по формуле (V=pi R^2H). Тогда объем первого относится к объему второго цилиндра как [dfrac{16}{V_2}=dfrac{pi,R_1^2,H_1}{pi,R_2^2,H_2}=
left(dfrac{R_1}{R_2}right)^2cdot dfrac{H_1}{H_2}] Из условие следует, что (R_1=frac17R_2), (H_2=frac18H_1), следовательно, [dfrac{16}{V_2}=left(dfrac{frac17R_2}{R_2}right)^2cdot
dfrac{H_1}{frac18H_1}=dfrac1{49}cdot 8 quadRightarrowquad
V_2=98.]
Ответ: 98
Задание
13
#3052
Уровень задания: Равен ЕГЭ
В сосуд, имеющий форму конуса, налили 75 грамм жидкости до половины высоты сосуда. Сколько грамм этой же жидкости нужно долить в сосуд, чтобы заполнить его доверху?

Заметим, что из формулы физики (V=frac{m}{rho}) – объем равен отношению массы к плотности.
Пусть (O) – центр основания большего конуса, (Q) – меньшего, а (S) – их общая вершина. В одной плоскости проведем радиусы (OA) и (QB), как показано на рисунке:

Тогда (QBparallel OA) и (triangle SQBsim triangle SOA). Следовательно, [dfrac{OA}{QB}=dfrac{OS}{QS}=dfrac21] так как по условию высота жидкости в два раза меньше высоты сосуда. Тогда для жидкости имеем: [m_{small{text{ж}}}=V_{small{text{ж}}}cdot rho=
dfrac13cdot picdot QScdot QB^2 cdot rho] Следовательно, весь сосуд вмещает этой же жидкости [m=Vrho=dfrac13cdot picdot OScdot OA^2cdot rho=
dfrac 13cdot picdot 2QScdot (2QB)^2cdot rho= 8cdot
left(dfrac13cdot picdot QScdot QB^2cdot rhoright)=8cdot
75=600 {small{text{грамм}}}] Значит, долить нужно [600-75=525 {small{text{грамм}}}]
Заметим, что в данной задаче использование плотности – чистая формальность.
Ответ: 525
Задание
14
#3055
Уровень задания: Сложнее ЕГЭ
В правильной четырехугольной пирамиде с высотой (h) через точку на боковом ребре, лежащую на расстоянии (frac13h) от плоскости основания, проведена плоскость, параллельная плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите объем полученной меньшей пирамиды, если объем исходной пирамиды равен (54).
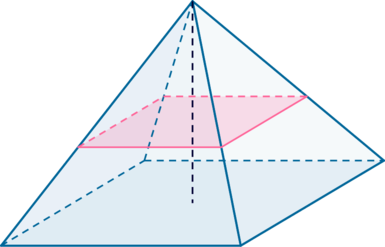
Пусть плоскость провели через точку (A’) на ребре (AS). Так как плоскость параллельна плоскости основания, то она пересечет боковые грани по прямым (A’B’, B’C’, C’D’, D’A’), параллельным соответственно (AB, BC, CD, DA), причем (SA’B’C’D’) – тоже правильная четырехугольная пирамида.
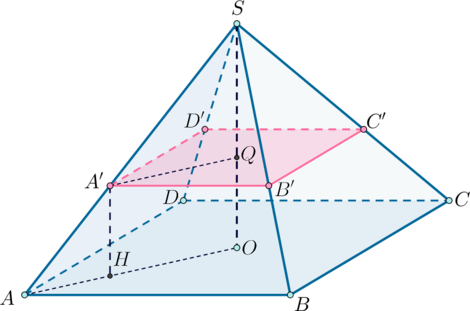
Рассмотрим плоскость (ASO). Проведем (A’Hparallel SO) ((SO) — высота исходной пирамиды). Тогда (A’Hperp ABC). Следовательно, это и есть расстояние, равное (frac13SO), на котором от плоскости основания проведена (розовая) плоскость.
(triangle AA’Hsim triangle ASO), следовательно, [dfrac{SA}{AA’}=dfrac{SO}{A’H}=3 quadRightarrowquad
SA=3AA’ quadRightarrowquad SA’=dfrac23SA] Также отсюда следует, что (SQ=frac23SO).
(triangle ASBsim triangle A’SB’), следовательно, [dfrac23=dfrac{SA’}{SA}=dfrac{A’B’}{AB} quadRightarrowquad
A’B’=dfrac23AB] Таким образом, объемы маленькой и большой пирамид относятся как [dfrac{V_{{small{text{м}}}}}{V_{small{text{б}}}}=
dfrac{frac13cdot SQcdot A’B’^2}{frac13cdot SOcdot
AB^2}=dfrac{SQ}{SO}cdot
left(dfrac{A’B’}{AB}right)^2=dfrac23cdot
left(dfrac23right)^2=dfrac8{27}] Следовательно, объем маленькой пирамиды равен [V_{{small{text{м}}}}=dfrac8{27}cdot 54=16.]
Ответ: 16
Источник
