Есть два сосуда в одном 30кг
При решении задач на сплавы и смеси считают, что сумма масс сплавляемых веществ равна массе получаемого сплава, что сумма масс вещества, входящего в сплавы равна массе этого вещества в полученном сплаве. Аналогичное допущение принимаем и для сумм масс (объёмов) при смешивании жидкостей.
Рассмотрим подготовительную задачу.
Задача 1. Имеется уксусный раствор массой 1,5 кг, содержащий 40 % уксуса. Сколько килограммов воды нужно добавить в раствор, чтобы новый раствор содержал 10 % уксуса?
Решение. I способ.
1) 40 : 10 = 4 (раза) — во столько раз уменьшилась концентрация уксуса в растворе и увеличилась масса раствора,
2) 1,5 * 4 = 6 (кг) — масса нового раствора,
3) 6 – 1,5 = 4,5 (кг) — воды надо добавить.
II способ. 1) 0,4 * 1,5 = 0,6 (кг) — масса уксуса в первом растворе.
2) Пусть добавили x кг воды. Составим уравнение:
0,1(1,5 + x) = 0,6.
Оно имеет единственный корень 4,5. Значит, надо добавить 4,5 кг воды.
Ответ. 4,5 кг.
Рассмотрим способы решения задач на смеси и сплавы из сборников вариантов для подготовки к ЕГЭ.
Задача 2. (2017) В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
Задача 3. (2018) Имеется два сплава. Первый содержит 25 % никеля, второй — 30 % никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 28 % никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение. Пусть масса первого сплава x кг, второго (150 – x) кг, третьего — 150 кг. Найдём массу никеля в каждом из трёх сплавов. Никеля было
в первом сплаве 0,25x кг,
во втором — 0,3(150 – x) кг,
в третьем — 0,28 *150 = 42 (кг).
Составим уравнение:
0,25x + 0,3(150 – x) = 42.
Решив уравнение, получим его единственный корень x = 60. Теперь ответим на вопрос задачи. Масса первого сплава 60 кг, масса второго сплава 90 кг, первая меньше второй на 30 кг.
Ответ. На 30 кг.
Задача 4. (2019) Первый сплав содержит 5 % меди, второй — 14 % меди. Масса второго сплава больше массы первого сплава на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
Решение. Пусть масса первого сплава x кг, второго (x + 7) кг, третьего — (2x + 7) кг. Меди было в первом сплаве 0,05x кг, во втором — 0,14(x + 7) кг, в третьем — 0,1(2x + 7) кг. Составим уравнение:
0,05x + 0,14(x + 7) = 0,1(2x + 7).
Решив уравнение, получим его единственный корень x = 28. При x = 28 масса третьего сплава 2x + 7 равна 63 кг.
Ответ. 63 кг.
Задача 5. (2017) Смешав 70 %-й и 60 %-й растворы кислоты и добавив 2 кг чистой воды, получили 50 %-й раствор кислоты. Если бы вместо 2 кг воды добавили 2 кг 90 %-го раствора той же кислоты, то получили бы 70 %-й раствор кислоты. Сколько килограммов 70 %-го раствора кислоты использовали для получения смеси?
Решение. Пусть масса первого раствора x кг, второго y кг. Приравняв массы кислоты до смешивания и после смешивания, составим два уравнения:
0,7x + 0,6y = 0,5(x + y + 2),
0,7x + 0,6y + 0,9*2 = 0,7(x + y + 2).
Решив систему этих двух уравнений, получим её единственное решение:
x = 3, y = 4. Использовали 3 кг 70 %-го раствора кислоты.
Ответ. 3 кг.
Задача 6. (2017) Имеется два сосуда. Первый содержит 100 кг, а второй — 50 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 28 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Для второго смешивания возьмём 1 кг первого раствора и 1 кг второго, получим 2 кг смеси. Составим первое уравнение:
Решив систему уравнений (1) и (2), получим её единственное решение: x = 12, y = 60. В первом сосуде содержится x * 100 / 100 = 12 (кг) кислоты. Ответ. 12 кг.
Для самостоятельного решения
7. Имеется 400 г морской воды, содержащей 4 % соли. Сколько граммов чистой воды нужно добавить в эту морскую воду, чтобы новый раствор содержал 2 % соли?
8. (2016) В сосуд, содержащий 10 литров 24-процентного водного раствора некоторого вещества, добавили 5 литров воды. Определите процентную концентрацию того же вещества в новом растворе.
9. (2009) В бидон налили 4 литра молока трёхпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?
10. (2017) Имеется два сплава. Первый содержит 5 % никеля, второй — 20 % никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 15 % никеля. На сколько килограммов масса первого сплава меньше массы второго?
11. (2017) Первый сплав содержит 5 % меди, второй — 11 % меди. Масса второго сплава больше массы первого сплава на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10 % меди. Найдите массу третьего сплава.
12. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?
13. В первом сплаве отношение массы олова к массе свинца 2 : 3, во втором 1 : 5. В каком отношении надо взять массы этих сплавов, чтобы получить третий сплав с отношением массы олова к массе свинца 1 : 2?
Ответы. 7. 400 г. 8. 16 %. 9. 4,8 %. 10. На 75 кг. 11. 6 кг. 12. 5 : 2. 13. 5 : 2.
Для работы с задачами в классе можно использовать вариант заметки в виде презентации: Сплавы и смеси. Задачи 11 из ЕГЭ.
Источник
ÐадаÑа â807 из 1084 |
ÐмеÑÑÑÑ Ð´Ð²Ð° ÑоÑÑда, ÑодеÑжаÑие 10 кг и 16 кг ÑаÑÑвоÑа киÑлоÑÑ ÑазлиÑной конÑенÑÑаÑии. ÐÑли Ð¸Ñ ÑлиÑÑ Ð²Ð¼ÐµÑÑе, Ñо полÑÑиÑÑÑ ÑаÑÑвоÑ, ÑодеÑжаÑий 55% киÑлоÑÑ. ÐÑли же ÑлиÑÑ ÑавнÑе маÑÑÑ ÑÑÐ¸Ñ ÑаÑÑвоÑов, Ñо полÑÑеннÑй ÑаÑÑÐ²Ð¾Ñ Ð±ÑÐ´ÐµÑ ÑодеÑжаÑÑ 61% киÑлоÑÑ. СколÑко килогÑаммов киÑлоÑÑ ÑодеÑжиÑÑÑ Ð² пеÑвом ÑаÑÑвоÑе?
РеÑение задаÑи:
Ðведем обознаÑениÑ:
x – конÑенÑÑаÑÐ¸Ñ ÐºÐ¸ÑлоÑÑ Ð² пеÑвом ÑоÑÑде.
10x – маÑÑа киÑлоÑÑ Ð² 10 кг ÑаÑÑвоÑа в пеÑвом ÑоÑÑде, Ñ.е. Ñо ÑÑо надо найÑи в задаÑе.
y – конÑенÑÑаÑÐ¸Ñ ÐºÐ¸ÑлоÑÑ Ð²Ð¾ вÑоÑом ÑоÑÑде.
16y – маÑÑа киÑлоÑÑ Ð² 16 кг ÑаÑÑвоÑа во вÑоÑом ÑоÑÑде.
СоÑÑавим ÑÑавнение Ð´Ð»Ñ Ð¿ÐµÑвого ÑÑловиÑ:
10x+16y=26*0,55 (26 – ÑÑо маÑÑа нового ÑаÑÑвоÑа 10+16, 0,55 – конÑенÑÑаÑÐ¸Ñ Ð½Ð¾Ð²Ð¾Ð³Ð¾ ÑаÑÑвоÑа).
10x+16y=14,3
10x=14,3-16y
СоÑÑавим ÑÑавнение Ð´Ð»Ñ Ð²ÑоÑого ÑÑловиÑ:
10x+10y=20*0,61
10x+10y=12,2
ÐодÑÑавлÑем во вÑоÑое ÑÑавнение знаÑение 10Ñ
:
14,3-16y+10y=12,2
14,3-6y=12,2
6y=14,3-12,2
6y=2,1
y=0,35
ÐодÑÑавлÑем знаÑение y в пеÑвое ÑÑавнение:
10x=14,3-16y
10x=14,3-16*0,35
10x=8,7
ÐÑвеÑ: 8,7
ÐоделиÑеÑÑ ÑеÑением
ÐÑиÑоединÑйÑеÑÑ Ðº нам…
ÐÑ Ð¼Ð¾Ð¶ÐµÑе поблагодаÑиÑÑ Ð°Ð²ÑоÑа, напиÑаÑÑ Ñвои пÑеÑензии или пÑÐµÐ´Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ Ð½Ð°
ÑÑÑаниÑе ‘ÐÑо нађ
ÐÑÑгие задаÑи из ÑÑого Ñаздела

ÐадаÑа âF1A0A9
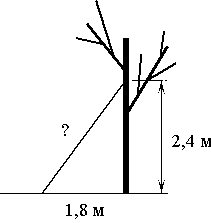 Ðакова длина (в меÑÑаÑ
) леÑÑниÑÑ, коÑоÑÑÑ Ð¿ÑиÑлонили к деÑевÑ, еÑли веÑÑ
ний ÐµÑ ÐºÐ¾Ð½ÐµÑ Ð½Ð°Ñ
одиÑÑÑ Ð½Ð° вÑÑоÑе 2,4 м над землÑй, а нижний оÑÑÑÐ¾Ð¸Ñ Ð¾Ñ ÑÑвола деÑева на 1,8 м?
Ðакова длина (в меÑÑаÑ
) леÑÑниÑÑ, коÑоÑÑÑ Ð¿ÑиÑлонили к деÑевÑ, еÑли веÑÑ
ний ÐµÑ ÐºÐ¾Ð½ÐµÑ Ð½Ð°Ñ
одиÑÑÑ Ð½Ð° вÑÑоÑе 2,4 м над землÑй, а нижний оÑÑÑÐ¾Ð¸Ñ Ð¾Ñ ÑÑвола деÑева на 1,8 м?

ÐадаÑа â23E335
 РадиÑÑ Ð¾ÐºÑÑжноÑÑи, опиÑанной около ÑавноÑÑоÑоннего ÑÑеÑголÑника, Ñавен 16. ÐайдиÑе вÑÑоÑÑ ÑÑого ÑÑеÑголÑника.
РадиÑÑ Ð¾ÐºÑÑжноÑÑи, опиÑанной около ÑавноÑÑоÑоннего ÑÑеÑголÑника, Ñавен 16. ÐайдиÑе вÑÑоÑÑ ÑÑого ÑÑеÑголÑника.

ÐадаÑа âEA6181
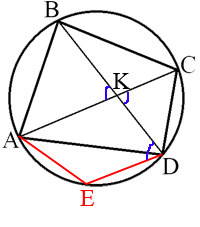 ЧеÑÑÑÑÑ
ÑголÑник ABCD Ñо ÑÑоÑонами AB=19 и CD=22 впиÑан в окÑÑжноÑÑÑ. Ðиагонали AC и BD пеÑеÑекаÑÑÑÑ Ð² ÑоÑке K, пÑиÑÑм â AKB=60°. ÐайдиÑе ÑадиÑÑ Ð¾ÐºÑÑжноÑÑи, опиÑанной около ÑÑого ÑеÑÑÑÑÑ
ÑголÑника.
ЧеÑÑÑÑÑ
ÑголÑник ABCD Ñо ÑÑоÑонами AB=19 и CD=22 впиÑан в окÑÑжноÑÑÑ. Ðиагонали AC и BD пеÑеÑекаÑÑÑÑ Ð² ÑоÑке K, пÑиÑÑм â AKB=60°. ÐайдиÑе ÑадиÑÑ Ð¾ÐºÑÑжноÑÑи, опиÑанной около ÑÑого ÑеÑÑÑÑÑ
ÑголÑника.

ÐадаÑа âFC7964
Ðакие из даннÑÑ
ÑÑвеÑждений веÑнÑ? ÐапиÑиÑе иÑ
номеÑа.
1) ÐÑли пÑи пеÑеÑеÑении двÑÑ
пÑÑмÑÑ
ÑÑеÑÑей пÑÑмой внÑÑÑенние накÑеÑÑ Ð»ÐµÐ¶Ð°Ñие ÑÐ³Ð»Ñ ÑÐ°Ð²Ð½Ñ 90°, Ñо ÑÑи две пÑÑмÑе паÑаллелÑнÑ.
2) РлÑбой ÑеÑÑÑÑÑ
ÑголÑник можно впиÑаÑÑ Ð¾ÐºÑÑжноÑÑÑ.
3) ЦенÑÑом окÑÑжноÑÑи, опиÑанной около ÑÑеÑголÑника, ÑвлÑеÑÑÑ ÑоÑка пеÑеÑеÑÐµÐ½Ð¸Ñ ÑеÑединнÑÑ
пеÑпендикÑлÑÑов к ÑÑоÑонам ÑÑеÑголÑника.

ÐадаÑа â55503E
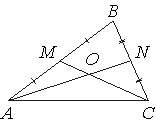
 ТоÑки M и N ÑвлÑÑÑÑÑ ÑеÑединами ÑÑоÑон AB и BC ÑÑеÑголÑника ABC ÑооÑвеÑÑÑвенно. ÐÑÑезки AN
ТоÑки M и N ÑвлÑÑÑÑÑ ÑеÑединами ÑÑоÑон AB и BC ÑÑеÑголÑника ABC ÑооÑвеÑÑÑвенно. ÐÑÑезки AN
и CM пеÑеÑекаÑÑÑÑ Ð² ÑоÑке O, AN=21, CM=15. ÐайдиÑе OM.
Источник
