Физические законы движения жидкостей по сосудам
Движение крови подчиняется физическим и физиологическим закономерностям.
Физические – законы гидродинамики.
- 1-й закон: количество протекающей по сосудам крови и скорость её движения зависит от разности давления в начале и конце сосуда. Чем эта разница больше, тем лучше кровоснабжение.
- 2-й закон: движению крови препятствует периферическое сопротивление.
Физиологические закономерности движения крови по сосудам:
- работа сердца;
- замкнутость сердечно-сосудистой системы;
- присасывающее действие грудной клетки;
- эластичность сосудов.
В фазу систолы кровь поступает в сосуды. Стенка сосудов растягивается. В диастолу выброса крови нет, эластичная сосудистая стенка возвращается в исходное состояние, в стенке накапливается энергия. При снижении эластичности сосудов появляется пульсирующий кровоток (в норме – в сосудах малого круга кровообращения). В патологических склеротически изменённых сосудах – симптом Мюссе – движения головы в соответствии с пульсацией крови.
Гемодинамика — раздел физиологии кровообращения, использующий законы гидродинамики (физические явления движения жидкости в замкнутых сосудах) для исследования причин, условий и механизмов движения крови в сердечно-сосудистой системе. Гемодинамика определяется двумя силами:
- давлением, которое оказывает влияние на жидкость,
- сопротивлением, которое она испытывает при трении о стенки сосудов и вихревых движениях.
Силой, создающей давление в сосудистой системе, является сердце. У человека среднего возраста при каждом сокращении сердца в сосудистую систему выталкивается 60−70 мл крови (систолический объем) или 4−5 л/мин (минутный объем). Движущей силой крови служат разность давлений, возникающая в начале и конце трубки.
Почти во всех отделах сосудистой системы кровоток носит ламинарный характер — кровь движется отдельными слоями параллельно оси сосуда. При этом слой, прилежащий к стенке сосуда, остается практически неподвижным, по этому слою скользит второй, а по нему, в свою очередь, третий и т.д. Форменные элементы крови составляют центральный, осевой поток, плазма движется ближе к стенке сосуда. Следовательно, чем меньше диаметр сосуда, тем ближе располагаются центральные слои к стенке и больше тормозится скорость их движения из-за вязкого взаимодействия со стенкой. В целом это означает, что в мелких сосудах скорость кровотока ниже, чем в крупных. В правильности этого положения легко убедиться сопоставив скорости кровотока в разных участках сосудистого русла. В аорте она составляет 40 см/с, в артериях — от 40 до 10, артериолах — 10 — 0,1, капилляра — меньше 0,1, венулах — меньше 0,3, венах — 0,3 — 5,0, полой вене — 5 — 20 см/с (К. Шмидт-Ниельсон, 1982).
Наряду с ламинарным в сосудистой системе существует турбулентное движение с характерным завихрением крови. Ее частицы перемещаются не только параллельно оси сосуда, как при ламинарном кровотоке, но и перпендикулярно ей. Результатом такого сложного перемещения является значительное увеличение внутреннего трения жидкости. В этом случае объемная скорость тока крови будет уже не пропорциональной градиенту давления, а примерно равной квадратному корню из него. Турбулентное движение обычно возникает в местах разветвлений и сужений артерий, в участках крутых изгибов сосудов.
Кровь представляет собой взвесь форменных элементов в коллоидно-солевом растворе, она обладает определенной вязкостью, не являющейся величиной постоянной. При протекании крови через капилляр, диаметр которого меньше 1 мм, вязкость уменьшается.
Источник
Гемодинамика – раздел физиологии, изучающий причины, условия и механизмы движения крови в сердечно-сосудистой системе.
Движение крови по кровеносным сосудам подчиняется законам гемодинамики. В свою очередь, их можно рассматривать, как частный случай гидродинамики. Т.е. в основе законов движения крови лежат физические законы движения жидкости (воды) по сосудам (имеются в виду, не кровеносные сосуды)
Основным условием кровотока, как и в гидродинамике, является градиент давления между начальными и конечными отделами системы сосудов.
Давление в кровеносных сосудах создается работой сердца. Благодаря его насосной деятельности создается давление крови, которое способствует ее продвижению по сосудам. Во время систолы желудочков порции крови выбрасываются в аорту и легочные артерии под определенным давлением, что приводит к увеличению давления и растяжению эластических стенок сосудистого бассейна. Во время диастолы растянутые кровью артериальные сосуды сокращаются и проталкивают кровь к капиллярам, поддерживая тем самым, необходимое давление. Кровь течет из области высокого, в область низкого давления. При движении ей приходится преодолевать сопротивление, создаваемое, трением частиц крови друг о друга, т.е. внутреннее трение, а так же трением частиц крови о стенки сосудов, т.е. внешнее трение. По мере продвижения крови по сосудам от аорты к венам давление крови уменьшается. Особенно быстро снижается давление в артериолах и капиллярах, т.к. они обладают большим сопротивлением, имеют малый радиус, большую суммарную длину, многочисленные ветвления, создающие дополнительное препятствие кровотоку.
Основной закон гемодинамики. В соответствии с законами гидродинамики количество жидкости (крови), протекающей через поперечное сечение сосуда (Q), за единицу времени (мл/с) или объемная скорость кровотока (Q) прямо пропорциональна разности давления в начале (Р1) сосудистой системы, т.е. в аорте, и в ее конце (Р2), т.е. полых венах, и обратно пропорциональна сопротивлению(R) току крови.
Q= (P1 – P2) / R,
где, Q – объемная скорость крови;
Р1 – давление в аорте;
Р2 – давление в полых венах;
Р1-Р2 – разность давлений, имеющаяся в начале и в конце сосудистой системы, обеспечивает продвижение крови и способствует непрерывному кровотоку. Учитывая, что давление в полых венах равно 0, имеем:
Q=Р/R, где
Р – давление в аорте. Следовательно, Р=QR.
В данном случае Q – это минимальный объем кровотока, который зависит только от насосной функции сердца и определяется по формуле:
МОК= СО х ЧСС,
Где СО – систолический объем;
ЧСС – частота сердечных сокращений.
Т.о. МОК – это количество крови, протекающее в единицу времени (1мин) через поперечное сечение какого-либо участка кровеносного русла. Подставляя его в формулу расчета давления, имеем
Р = СО х ЧСС х R
В связи с замкнутостью кровеносной системы объемная скорость кровотока во всех его отделах (всех артериях, всех капиллярах, всех венах) одинакова и составляет 4-6 л/ мин.
Теперь необходимо определить и выразить R.
R – сопротивление в кровеносном сосуде, его можно определить по формуле Пуазейля: R=8lη/πr4, где
где l – длина сосудов;
η – вязкость крови;
π – константа (число), показывающее отношение окружности к диаметру, всегда равна 3,14;
r – радиус сосуда.
Т.е. сопротивление зависит от длины сосудов, вязкости крови (которая в 5 раз больше вязкости воды), радиуса сосуда. Длина сосуда постоянна, радиус и вязкость – переменные величины. Вязкость крови определяется содержанием в крови форменных элементов, преимущественно эритроцитов и белков, т.е. гематокритом. При уменьшении количества эритроцитов (при анемии) вязкость крови низкая, сопротивление уменьшается. При увеличении количества эритроцитов (эритроцитоз) вязкость крови увеличиваются, сосудистое сопротивление становится выше. Однако, несмотря на то, что вязкость – это переменная величина, организм тем не менее, не имеет возможности изменять ее быстро. Т.е. с точки зрения быстроты регуляции давления вязкость так же можно считать константой. Убирая из формулы Пуазейля все константы, получаем
R ~ 1/r4.
Эта формула показывает, что сопротивление току крови обратно пропорциональна радиусу. Например, чем больше радиус, тем меньше сопротивление.
Обратим внимание, что математическому (физическому) понятию радиуса в физиологии соответствует понятие тонуса сосуда. Эти величины обратно пропорциональны, например, если тонус сосуда увеличивается (гладкомышечные клетки стенок сосуда сокращаются), то его радиус уменьшается, а сопротивление току крови при этом возрастает.
Тонус сосуда ~ 1/r
R ~ (тонус сосуда)4
Причем, зависимость R от радиуса (тонуса) сосуда сильная, в формуле радиус находится в четвертой степени. Значит, даже незначительное изменение радиуса сосудов будет сильно влиять на сопротивление току крови и, следовательно, на давление в сосуде.
Подставляя выражение R в формулу расчета артериального давления, имеем
Р = СО х ЧСС/r4
Эту формулу можно считать базовой для гемодинамики, по крайней мере, для расчета значения давления в магистральных артериях. В клинике именно давление в крупных артериях называют артериальным давлением.
Полученная формула весьма информативна. Она в частности, показывает, какие возможности имеет организм, чтобы быстро изменить артериальное давление. Он может изменить три параметра: СО, ЧСС и r. При этом понятно, что наиболее выражено давление будет меняться при изменении тонуса сосудов (r в четвертой степени).
Кроме того, на основе формулы понятно, что артериальное давление в основном зависит от работы двух систем организма сердца и сосудов. При этом сердце, благодаря своей насосной функции, формирует некий общий уровень давления (МОК= СО х ЧСС), а для его регуляции в основном используется тонус сосудов (R ~ 1/r4.).
Можно так же утверждать, что систолическое давление в основном зависит от работы сердца и характеризует его насосную функцию. Тогда как диастолическое давление в основном определяется эластическими свойствами артерий и характеризует их тонус.
Линейная и объемная скорости кровотока.Общий объем крови в сосудистой системе является важным гомеостатическим показателем. Средняя величина составляет для женщин 6-7%, для мужчин 7-8% от массы тела и находится в пределах 4-6 л. Из этого объема 80-85% крови заполняет большой круг кровообращения, около 10% малый круг кровообращения, 7% находится в сердце.
Объемная скорость кровотока – объем крови, протекающей через поперечное сечение данного отдела сосуда в единицу времени. Измеряется в мл/сек.
Объемная скорость кровотока одинакова во всех отделах сосудистой системы. Очевидно, что если в конкретный момент времени левый желудочек выбрасывает в аорту 70 мл крови, то в то же время в правое предсердие будет притекать такое же количество крови (70 мл), равно кК через капилляры будет проталкиваться объем крови, равный 70 мл. Объемная скорость за минуту соответствует МОК.
Зная объемную скорость кровотока можно рассчитать его линейную скоростьили расстояние, на которое перемещается частица крови в единицу времени, или скорость движения крови в сосудах. Измеряется в м/с.
Линейная скорость, вычисленная по формуле V=Q/π r, где
V – линейная скорость кровотока ( м/с);
Q – объемная скорость(мл/с);
π – число пи;
r – радиус поперечного сечения конкретного отдела кровеносной системы.
Если Q одинакова во всех участках кровеносной системы, то V сильно варьирует и зависит, как это следует из формулы, от суммарного радиуса всех сосудов данного участка кровеносной системы. Самым узким из них является аорта, радиус которой 2,5 см (25 мм), поэтому скорость кровотока здесь максимальна – 0,5 м/с. Наиболее широкий участок – капилляры большого круга кровообращения, суммарный радиус которых в среднем в 600 раз больше аорты (1500 мм или 15 м). Соответственно, здесь скорость кровотока падает в 600 раз и составляет 0,5-1,0 мм/с. Суммарный диаметр (радиус) обеих полых вен в 2 раза больше аорты, кровь течет в них со скоростью 25 см/с. Из формулы и приведенных цифр следует, что V связана с радиусов сосудов линейно и обратно пропорционально.
В центре сосуда линейная скорость максимальна, около стенок минимальна, т.к. велико трение частиц крови о стенку. Более того, непосредственно у стенок сосудов трение столь велико, что говорят о краевом стоянии форменных элементов, т.е. они движутся предельно медленно.
Давление в различных участках кровеносного русла.
Как и скорость кровотока, давление в сосудах обратно пропорционально их радиусу. Наиболее высоким оно оказывается в аорте и равно 140/90 мм рт. ст. 120 мм рт. ст. – систолическое давление, соответствует момента выброса СО из сердца. 90 мм рт. ст. – диастолическое давление, формируется благодаря эластическим волокнам аорты в моменты времени, когда сердце не выполняет свою насосную функцию.
Более широким участком кровеносной системы являются крупные магистральные артерии, соответственно, давление здесь чуть ниже, чем в аорте, и составляет 120/80 мм рт. ст. Еще совсем недавно такое АД, измеряемое на лучевой артерии, считалось в клинике нормальным. Однако в настоящее время, в связи с высоким общим стрессогенным фактором, характерным для современной цивилизации, гиподинамией, в которой существует большинство людей в развитом обществе, клинической нормой АД принимают 139/89 мм рт. ст.
Согласно выше определенной формуле расчета сосудистого давления – Р ~ Q/r4, оно (давление) должно линейно и обратно пропорционально зависеть от радиуса в любом участке кровеносного русла. Однако такая линейная зависимость характерна в основном только для артерий, в капиллярах и венах присутствует ряд сил, факторов, которые значимо влияют на давление, но не учитываются в данной формуле.
Радиус (диаметр) капиллярного русла в 600 раз больше аорты, следовательно, в гидродинамической системе давления в них будет снижаться в 600 раз. Тогда как гемодинамической системе давление в капиллярах падает всего в несколько раз и составляет и 10-25 мм рт. ст. Это происходит вследствие резкого увеличения сопротивления току крови в обменных сосудах. Дело в том, что диаметр отдельно взятого капилляра меньше диаметра эритроцита, который вынужден протискиваться через капилляр. При этом сила трения столь возрастает, что эритроцит, проходя через обменный сосуд, изменяет свою форму, становясь элипсовидным. Это с одной стороны, улучшает диффузию СО2 и О2, с другой – препятствует значительному падению давления в сосуде.
Диаметр полых вен в 2 раза больше аорты. Если бы стенки этих сосудов были жесткими, то давление в полых венах было бы в 2 раза ниже, чем в аорте. На самом деле давление в полых венах равно 0. Это происходит, потому что стенки полых вен, содержащие коллаген, хорошо растягиваются, не оказывая сопротивление току крови. Если R=0, то и Р=0 (Р=QR). Более того, в момент диастолы, когда сердце расслабляется, давление в полых венах становится даже отрицательным. Говорят о присасывающей функции сердца, которая облегчает возврат крови из большого круга кровообращения, уменьшая, тем самым, нагрузку на сердечную мышцу. Давление в венах меньшего диаметра, чем полые, чуть выше, чем в них, но меньше, чем в капиллярах – 5-15 мм рт. ст. Наконец отметим, что в капиллярах и венах нет пульсового давления (систолического, диастолического), т.к. нет пульсовой волны из – за отсутствия эластических волокон в стенках этих сосудов.
Источник
Для расчета движения воды в трубопроводе нужно знать не так уж и много. Для этого не надо глубоко изучать физику, но всё же некоторое основные понятия изучить придется.
В этой статье я приведу самые основные формулы, которые вам пригодятся не только для расчетов, но и для общего понимания, что может влиять в вашем водопроводе на его течение. Иногда общее понимание процессов поможет вам избежать ошибок при монтаже системы.
Например, не все знают, что в части водопровода с трубами меньшего диаметра давление на стенки меньше, чем на участке с трубами большего диаметра. Почему возникает кавитация и вообще, что это такое. А это надо знать.
Статья будет обновляться и дополняться.

Уравнение неразрывности
Для жидкости, текущей в трубе, этот закон используют в такой форме (называемой уравнением неразрывности):
v⋅S = const
Где v – скорость жидкости S – площадь сечения трубы, по которой течёт жидкость. Сформулировать этот закон можно и так:
Сколько вливается жидкости в ёмкость, в данном случае в трубу, столько должно и выливаться, если условия течения не изменяются.
Скорость в узких участках трубы должна быть выше, чем в широких.
Подробнее об этом можно прочитать в статье Основные понятия гидродинамики. Уравнение непрерывности.
Уравнение Бернулли стационарного движения
Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 – 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.
Идеальная жидкость – жидкость, в которой отсутствуют силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда.
Уравнение стационарного движения, носящее его имя, имеет вид:
| P + | ρ⋅v² | + ρ⋅g⋅h = const |
| 2 |
где P – давление жидкости, ρ − её плотность, v – скорость движения, g – ускорение свободного падения, h – высота, на которой находится элемент жидкости.
Смысл уравнения Бернулли в том, что внутри системы заполненной жидкостью (участка трубопровода) общая энергия каждой точками всегда неизменна.
В уравнении Бернулли есть три слагаемых:
- ρ⋅v2/2 – динамическое давление – кинетическая энергия единицы объёма движущей жидкости;
- ρ⋅g⋅h – весовое давление – потенциальная энергия единицы объёма жидкости;
- P – статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии (“энергии давления”).
Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.
Явление кавитации
Кавитация (от латинского cavitas – “углубление”, “полость”) – процесс образования полостей (пузырьков) в движущейся жидкости вследствие понижения давления.
Явление кавитации также объясняется уравнением Бернулли. Если скорость течения жидкости значительно возрастает, то давление сильно понизится – настолько, что жидкость закипит. Такую скорость можно получить, если пропускать жидкость через очень узкий участок трубы или при быстром обращении лопатки в водяном насосе.
Пузырьки по ходу движения жидкости попадают в области жидкости с нормальным давлением и там схлопываются. Это схлопывание сопровождается гидродинамическими эффектами, способными привести к разрушению трубы или стенок насоса.
Гидродинамика Эйлера и Навье-Стокса
Уравнение Бернулли позволяет объяснить очень много интересных гидродинамических явлений, но гораздо больше явлений, происходящих в движущихся жидкостях и газах, с его помощью объяснить нельзя, потому что этот закон для идеальной жидкости, т.е для жидкости, которая не обладает внутренним трением, а значит не создает гидравлическое сопротивление..
Реальная жидкость отличается от идеальной и обладает внутренним трением, или по другому называют вязкостью. Два соприкасающиеся элемента жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый.
Закон вязкого трения Ньютона
Ньютон предположил, что величина этой силы (называемой силой внутреннего трения) пропорциональна разности скоростей элементов жидкости. Следовательно, сила внутреннего трения F пропорциональна изменению скорости жидкости v в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости:
η − коэффициент динамической вязкости.
Жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются ньютоновскими, или жидкостями с линейной вязкостью.
Величину коэффициента динамической вязкости (и справедливость данного закона) Ньютон определил с помощью несложного опыта: он передвигал по поверхности жидкости пластинку с той или иной скоростью. Для того чтобы поддерживать эту скорость постоянной, требовалась сила, которая при небольшой глубине жидкости оказалась прямо пропорциональна площади S и скорости пластинки v и обратно пропорциональна глубине жидкости h:
И хотя при увеличении глубины жидкости h сила вязкого трения пластинки не становится исчезающе малой, эта формула довольно точно описывает взаимодействие между соприкасающимися элементами жидкости.
Чем больше разность скоростей, тем больше сила, с которой они воздействуют друг на друга, заставляя притормаживать слишком быстро движущиеся элементы и разгоняя слишком медленные.
В результате относительное движение в жидкости прекращается (но иногда это может произойти не очень скоро).
Уравнение Навье – Стокса для вязких жидкостей
В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье – Стокса. Оно учитывает сжимаемость жидкостей и газов и, в отличие от закона Ньютона, справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости (у поверхности твёрдого тела в случае несжимаемой жидкости уравнение Навье – Стокса и закон Ньютона совпадают).
Любые газы, для которых выполняется условие сплошной среды, подчиняются и уравнению Навье – Стокса, т.е. являются ньютоновскими жидкостями.
Вязкость жидкости и газа обычно существенна при относительно малых скоростях, потому иногда говорят, что гидродинамика Эйлера – это частный (предельный) случай больших скоростей гидродинамики Навье – Стокса.
При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости (что впервые обнаружил и обосновал Ньютон).
Критерий Рейнольдса
Такую зависимость вывел английский физик и инженер Осборн Рейнольдс (1842 – 1912).
Критерий, который помогает ответить на вопрос, есть ли необходимость учитывать вязкость, является число Рейнольдса Re. Оно равно отношению энергии движения элемента текущей жидкости к работе сил внутреннего трения.
Рассмотрим кубический элемент жидкости с длиной ребра n. Кинетическая энергия элемента равна:
Согласно закону Ньютона, сила трения, действующая на элемент жидкости, определяется так:
Работа этой силы при перемещении элемента жидкости на расстояние n составляет
A = F⋅n = η⋅v⋅n²
а отношение кинетической энергии элемента жидкости к работе силы трения равно
| Eкин | = | ρ⋅n³⋅v² | ||
| A | 2⋅ η⋅v⋅n² |
Сокращаем и получаем:
Re – называется числом Рейнольдса.
Таким образом, Re – это безразмерная величина, которая характеризует относительную роль сил вязкости.
Например, если размеры тела, с которым соприкасаются жидкость или газ, очень малы, то даже при небольшой вязкости Re будет незначительно и силы трения играют преобладающую роль. Наоборот, если размеры тела и скорость велики, то Re >> 1 и даже большая вязкость почти не будет влиять на характер движения.
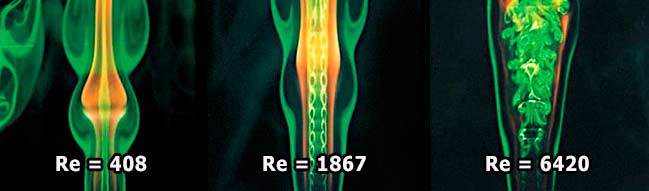
Однако не всегда большие числа Рейнольдса означают, что вязкость не играет никакой роли. Так, при достижении очень большого (несколько десятков или сотен тысяч) значения числа Re плавное ламинарное (от латинского lamina – “пластинка”) течение превращается в турбулентное (от латинского turbulentus – “бурный”, “беспорядочный”), сопровождающееся хаотическими, нестационарными движениями жидкости. Этот эффект можно наблюдать, если постепенно открывать водопроводный кран: тонкая струйка течёт обычно плавно, но с увеличением скорости воды плавность течения нарушается. В струе, вытекающей под большим напором, частицы жидкости перемещаются беспорядочно, колеблясь, всё движение сопровождается сильным перемешиванием.
Появление турбулентности весьма существенно увеличивает лобовое сопротивление. В трубопроводе скорость турбулентного потока меньше скорости ламинарного потока при одинаковых перепадах давления. Но не всегда турбулентность плоха. В силу того что перемешивание при турбулентности очень значительно, теплообмен – охлаждение или нагревание агрегатов – происходит существенно интенсивнее; быстрее идёт распространение химических реакций.
Источник
