Физика 7 класс сообщающиеся сосуды формула

Статьи
Основное общее образование
Линия УМК А. В. Перышкина. Физика (7-9)
Физика
Все мы ежедневно пользуемся сообщающимися сосудами – это чайник, лейка, в общем, это любая система ёмкостей, в которых жидкость, к примеру, вода, может свободно перетекать из одной ёмкости в другую. В чайнике, например, такими ёмкостями являются корпус и носик или корпус чайника и специальная ёмкость для определения уровня воды в нём. Что особенного в сообщающихся сосудах? Каким свойством или свойствами они обладают? Чем заслуживают наше внимание?
26 апреля 2019
Закон сообщающихся сосудов
Сосуды соединенные между собой, жидкость в которых может свободно перетекать, имеющие общее дно, называются сообщающимися. В соответствии с законом Паскаля, жидкость передаёт оказываемое на неё давление во всех направлениях одинаково. В открытых сосудах, атмосферное давление над каждым из них одинаково, значит, и давление жидкости на стенки сосудов будет одинаковым на любом уровне. Так как давление жидкости прямо пропорционально её плотности и глубине, в случае одинаковой жидкости в сообщающихся сосудах на одинаковой глубине будет одинаковое давление, что и объясняет выравнивание уровней жидкости в них. В случае разных жидкостей, чтобы на одинаковой глубине было одинаковое давление, жидкость с меньшей плотностью должна иметь больший уровень в сравнении с жидкостью большей плотности. Т.е.
ρ1 / ρ2 = h2 / h1
Физика. 7 класс. Учебник
Учебник соответствует Федеральному государственному образовательному стандарту основного общего образования. Большое количество красочных иллюстраций, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.
Купить
Свойство сообщающихся сосудов
Возьмем несколько различных по размеру и форме открытых сосудов, проделаем в каждом из них отверстие и соединим отверстия в сосудах трубками, чтобы жидкость, которую мы будем наливать в один из них, могла свободно перетекать из одного сосуда в другой. Для большего эффекта, пожмем трубки, которые их соединяют и наполним один из сообщающихся сосудов водой. Теперь откроем трубки и увидим, что когда жидкость перестанет перетекать, то, вне зависимости от формы и размера сосудов, уровни жидкости в каждом будут совершенно одинаковыми. Или проведём иной опыт – возьмём пластиковую бутыль и срежем донышко, а крышку плотно прикрутим, проделаем в ней небольшое отверстие и вставим в него небольшой шланг, место соединения шланга и крышки бутыли сделаем герметичным с помощью пластилина. Теперь закрепим бутыль вверх дном, а шланг расположим параллельно бутыли открытым концом чуть выше её срезанного дна. Заполним бутыль жидкостью, например, подкрашенной водой. И вновь мы увидим, что вне зависимости от высоты сообщающихся сосудов, уровень воды в бутыли будет точно таким же, как и уровень воды в шланге. В этом и заключается первое и основное свойство сообщающихся сосудов: в открытых сообщающихся сосудах уровни одинаковой жидкости будут одинаковыми. Это замечательное свойство нашло широкое применение в практике, но об этом поговорим чуть позже. А теперь возьмём U-образную стеклянную трубку. Это тоже сообщающиеся сосуды, их, в данном случае, называют коленами трубки. В правое колено нальём воду и она, конечно же, перетечёт в левое колено так, что уровни воды в обоих коленах будут одинаковыми – мы уже знаем, что так и должно быть, хоть пока что и не знаем, почему. А теперь в левое колено, очень аккуратно, чтобы жидкости не смешивались, нальём керосин или подкрашенный спирт. И мы увидим, что теперь верхние уровни каждой жидкости в коленах будут отличаться. Уровень спирта или керосина будет выше уровня воды. Заглянем заодно в таблицу плотности жидкостей и увидим, что плотность керосина или спирта меньше плотности воды, а уровень, наоборот, выше. Из этого эксперимента можно сделать вывод – если в открытых сообщающихся сосудах налиты две разные жидкости, то уровень будет выше у той, чья плотность меньше. Иными словами, плотности жидкостей и их уровни будут обратно пропорциональными. Настала пора объяснить, почему так получается.
Читайте также:
Проекты на уроках физики: плюсы и минусы
Что такое радуга?
Почему море соленое?
Почему небо голубого цвета?
Применение на практике
Благодаря своим свойствам, сообщающиеся сосуды нашли широкое применение в различных технических и бытовых устройствах. Перечислим некоторые из них:
- измерители плотности,
- жидкостные манометры,
- определители уровня жидкости (водомерное стекло, к примеру),
- домкраты,
- гидравлические прессы,
- шлюзы,
- фонтаны,
- водопроводные башни и т.д.
Свойство сообщающихся сосудов реализуется не только в физике. Такая известная поговорка «Если где-то прибыло, значит где-то убыло» фактически напрямую связана со свойством сообщающихся сосудов и означает, что в окружающем нас мире всё взаимосвязано, а значит – стремится к равновесию. Когда человек смещает это равновесие в одну сторону, это немедленно сказывается в чём-то другом. Над этим стоит задуматься, не так ли?
Материал по физике на тему «Сообщающиеся сосуды» для 7 класса.
Методические советы учителям
- При изучении этой темы обязательно необходима демонстрация. Описанные в статье эксперименты обязательно нужно показать детям в живом исполнении.
- Желательно продемонстрировать принцип действия фонтана (это также довольно не сложно сделать своими руками).
- Обратите внимание учащихся на формулу для двух жидкостей – это обратная пропорция. На нескольких примерах поясните смысл обратной пропорциональности.
- Рассмотрите ситуацию с тремя жидкостями (решите соответствующую задачу).
- А вот действие шлюзов лучше всего продемонстрировать с помощью видео.
#ADVERTISING_INSERT#
Источник
Всем известно, что нужно сделать с чайником, чтобы из его носика полилась вода, – просто наклонить. А вот вопрос, можно ли перевести корабль через гору в море или другой водоем, вызовет у нас сомнение. Чтобы ответить на него, сначала следует узнать, что из себя представляют сообщающиеся сосуды.

Закон сообщающихся сосудов
Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.
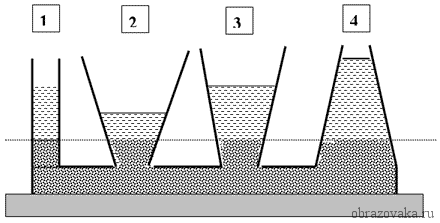
Рис. 1. Сообщающиеся сосуды
Закон сообщающихся сосудов гласит, что в таких сосудах, какую бы форму они не имели, поверхности однородных жидкостей в состоянии покоя находятся на одном уровне, то есть давление, оказываемое на стенки на любом горизонтальном уровне является одинаковым.
Если же в сосуде жидкости разные, то уровень выше в сосуде, в котором жидкость обладает меньшей плотностью. То есть, если в один сосуд налить жидкость, обладающую одной плотностью, а во второй – другой, то при равновесии их уровни не будут одинаковыми. Следовательно отсюда можно вывести формулу:
ρ1/ρ2=h2/h1
Где:
- ρ – плотность жидкости;
- h – высота столба.
Также для сообщающихся сосудов важной является формула:
p=gρh
Где:
- g – ускорение свободного падения;
- ρ – плотность жидкости (кг/куб.м);
- h – глубина (высота столба жидкости).
Этой формулой определяется давление жидкости на дно сосуда.
Древним римлянам было неизвестно определение сообщающихся сосудов, поэтому их акведуки – водопроводы занимали огромную протяженность над поверхностью земли и строились с равномерным уклоном вниз.
Свойства сообщающихся сосудов
В сообщающихся сосудах уровень жидкости одинаковый. Это происходит потому, что жидкость производит одинаковое давление на стенки сосуда. Достичь разного уровня однородной жидкости в сообщающихся сосудах можно с помощью перегородки между ними.
Перегородка перекроет сообщение между сосудами, и тогда можно в один из них долить жидкость, чтобы уровень изменился. В данной ситуации возникает напор – давление, производимое весом столба жидкости высотой, равной разности уровней. И если убрать перегородку, то именно это давление станет причиной тому, что жидкость будет перетекать в тот сосуд, где ее уровень ниже, до тех пор, пока уровни не станут одинаковыми.
В жизни очень часто можно встретить естественный напор. И таких примеров довольно много. Например, им обладает вода в горных реках, когда падает с высоты. Плотина также является примером естественного напора. Чем она выше, тем больше будет напор воды, поднятой плотиной.
Применение закона о сообщающихся сосудах
Принцип действия сообщающихся сосудов используется при сооружении фонтанов, водопроводов, шлюзов. Чайник и его носик тоже являются сообщающимися сосудами, так как вода, налитая в чайник, заполняет носик и всю остальную часть до одинаковой высоты. Применение свойств таких сосудов, могут даже помочь провести корабль через гору. И для этого как раз понадобиться шлюз. Шлюз – это лифт для судов. Если водное пространство перегорожено плотиной, то уровень воды в водохранилище выше, чем в реке ниже по течению. И чтобы добраться до этого уровня, судно должно зайти в шлюз, который отгорожен двумя водными непроницаемыми воротами. Когда шлюз полностью заполняется водой, судно выходит из шлюза и продолжает свой путь (уровень воды в шлюзе и водохранилище выравнивается по закону сообщающихся сосудов).

Рис. 2. Шлюз
Что мы узнали?
Из этой темы по физики за 7 класс можно ясно понять, какие сосуды называются сообщающимися. Ими могут называться лишь те сосуды, обладающие общим дном, где жидкость может свободно перетекать из одного сосуда в другой. Также сообщающиеся сосуды играют огромную роль в нашей повседневной жизни, облегчая ее и помогая выходить из трудных ситуаций. Принципы сообщающихся сосудов лежат в основе различных чайников, кофейников, водомерных стекол на паровых котлах.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-

Алика Квегмайр
10/10

Яна Василькова
10/10

Елена Куренкова
9/10

Мария Егорова
8/10

Тимофей Черный
10/10

Максим Скарнович
10/10

Люба Музыченко
10/10

Владимир Шитов
9/10

Константин Никитич
9/10

Катя Пу
10/10
Оценка доклада
Средняя оценка: 4.2. Всего получено оценок: 836.
Источник
Из-за перепадов высот реки имеют разные глубины, что затрудняет или даже делает невозможным движение по ним судов. Поэтому строят шлюзы, которые рассчитывают по принципу сообщающихся сосудов. Формулы, используемые для вычислений, были получены в результате теоретического анализа, а после подтверждены экспериментально. Эти правила применяют при строении фонтанов, гидравлических прессов, плотин и различных устройств.

Общие сведения
В древние времена перед человечеством возникла проблема доставки воды в свои жилища. Так появились акведуки, а после и водопроводные трубы, канализация. В те времена механизмы ещё не были придуманы, поэтому задача решалась с помощью природных сил. Суть изобретений заключалась в организации самотёка жидкости за счёт изменения высот желобов и труб.
Использование таких систем хоть и позволяло справляться с поставленной задачей, но приносило определённые неудобства. Работа трубопроводов заключалась в использовании свойств жидкости перетекать из одного места в другое за счёт изменения оказываемого давления.
В 1684 году Паскаль продемонстрировал парадокс. Для этого он использовал:
- закрытую бочку с водой;
- герметичную трубку;
- кружку.

Его опыт заключался в следующем. Один конец трубки был вставлен в бочку, а второй вертикально поднят на высоту порядка шести метров. В свободный конец Паскаль вылил кружку воды. Из-за малого диаметра трубки вода стала подниматься, а бочка лопнула. Как оказалось, в середине ёмкости создалось большое давление, привёдшее к её повреждению.
Этот парадокс объясняется законом Архимеда. Он гласит, что на тело, погруженное в воду, действует выталкивающая сила, равная весу жидкости. Значит, тело не сможет плавать в ней. Но это ошибочное рассуждение. Так как на самом деле архимедова сила появляется из-за гидростатического давления, зависящего от размера водяного столба, а не веса воды.
Поэтому тело и может находиться на поверхности резервуара, если его масса будет меньше веса воды. Это возможно, когда резервуар ненамного превышает размеры физического тела. Например, судно не тонет в ограниченном доке, так же как в и открытом океане, несмотря на то что масса воды между плавающим средством и стенами порта может быть меньше, чем вес корабля.
Закон Паскаля описывается формулой давления: P = F / S, где:
- p — давление;
- F — приложенная сила;
- S — площадь поверхности сосуда.
Из выражения следует, что увеличение силы на стенки удерживающие возрастает пропорционально. Давление принято изменять в ньютонах на квадратный метр или в паскалях. Этот закон нашёл применение в тормозных системах, гидравлических прессах.
Условие равновесия
Пусть имеются два сосуда, при этом они могут иметь разную форму и размеры. В нижней части они сообщаются, то есть соединяются с помощью трубки, которая имеет запорный вентиль. Ёмкость, стоящую слева, удобно обозначить цифрой один, соответственно, с правой стороны — два. В первую колбу можно налить жидкость, высота столба которой составляет h1. Её плотность пусть будет равняться p1. Во втором сосуде налито другое вещество с плотностью p и расстоянием от поверхности до дна h2.

Можно предположить, что высоты столбов подобраны так, что при открытии крана движение водного раствора не произойдёт. То есть он не будет перетекать из одной ёмкости в другую. Это важно для рассуждений, так как в другом случае жидкости просто перемешаются. Поэтому пусть растворы находятся в состоянии равновесия. Значит, давление и в первом, и во втором сосудах в нижних точках трубки будет одинаковым.
Действительно, если представить, что вместо крана стоит лёгкая перегородка, то для того, чтобы она осталась на своём месте, давление с её двух сторон должно быть скомпенсировано. Другими словами, в системе должны действовать одинаковые силы.
Так как растворы находятся в равновесии, то можно записать: P1 = P2. Давление можно выразить через плотность и высоту столба. Для рассматриваемого случая оно будет гидростатическим. Определяют его по формуле: p = ρ * g * h, где:
- ρ — плотность искомой жидкости;
- g — ускорение свободного падения;
- h — высота столба.
Полученное равенство справедливо как для первой, так и второй ёмкости. Его можно подставить в равенство равновесия: ρ1 * g * h1 = ρ2 * g * h2. После того как левую и правую часть сократить на g, формула примет вид: ρ1 * h1 = ρ2 * h2. Последнее выражение для сообщающихся сосудов и описывает условие равновесия.

Теперь можно рассмотреть частный случай, когда обе ёмкости заполнены однородной жидкостью. Это означает, что ρ1 = ρ2 = ρ. Условие равновесия примет вид: ρh1 = ρh2. Выражение можно сократить на плотность. Отсюда следует, что h1 = h2. Найденное правило называют математическим действием закона сообщающихся сосудов.
Опираясь на выведенную формулу, можно сформулировать закон словами. Но для этого нужно вспомнить, что такое h1 и h2. По сути, это расстояние от свободной поверхности жидкости, рассчитываемое по вертикали. Отсюда следует определение, что свободные поверхности однородной жидкости в соединённых ёмкостях устанавливаются на одинаковой высоте.
Опыт на сообщение
Чтобы открыть свой закон, Паскалю понадобилось использовать для опытов только два сосуда. Всё дело в том, что, согласно формуле, на установившийся уровень жидкости не влияет форма, размер, масса и другие характеристики. Если они сообщающиеся, то высота столба во всех ёмкостях будет одинаковой.

Для того чтобы самостоятельно убедиться в действии закона, можно провести простой эксперимент. Понадобится взять два любых шприца, наполнить один из них водой и соединить с другим трубочкой. Затем поднять их на любой уровень и убедиться, что водяная линия столбов будет находиться в одной горизонтали. Причём она не изменится даже при наклоне сосудов.
Проведённый опыт не будет называться полным, если не провести эксперимент с разными жидкостями. Так, если налить растворы с отличающейся плотностью, то можно наблюдать, что водяной столб не сможет выровняться.
Например, такое явление особо заметно, если попробовать смешать раствор поваренной соли и воды. Интересно то, что высота столба будет настолько меньше, насколько отличается плотность.
Решение примеров
В школе после рассмотрения темы преподаватель часто предлагает школьникам написать реферат или подготовить небольшое сообщение для видеоурока. В таком докладе, кроме теории, рекомендуется приводить несколько задач. Их решение желательно сопровождать рисунками, чтобы наглядно продемонстрировать в проекте, как работают сообщающиеся сосуды.
Физики обычно демонстрируют полезность явления на следующих двух примерах:

- Труба с площадью сечения S погружена в чашу со ртутью на одну треть. Не изменяя положение нижнего конца трубки, её наклон изменили на угол j. Определить, как поменялась высота. Если принять размер столба ртути за h, то, зная площадь сечения трубки, можно вычислить объём жидкости: V = S * h. Длину, которую занимает жидкость, можно определить так: l = h / cos (j). Значит, объём будет равняться: V1 = S * l = (S * h) / cos (j). Отсюда возможно определить изменение объёма в трубке: ΔV = V1 — V = (S * h) / c o s (j) — S * h. Так как площадь ёмкости равняется: S = π * D2 / 4, то искомая высота составит: Δh = Δ V * S = 4 * S * h * (1 − cos (j) / cos (j) * π * D 2 ).
- Какой площадью нужно изготовить отливной поршень в водяном прессе, чтобы выигрыш был в шесть раз? Площадь большого рычага равна двум метрам. Рассматриваемая система есть не что иное, как гидравлический пресс. То есть это два сообщающихся сосуда. Если принять, что большему поршню S соответствует сил F, а меньшему — S1 и F1, то по закону Паскаля они будут относиться друг к другу как F / S = F1 / S1. Из этого равенства можно выразить искомую площадь: S1 = F1 * S / F. Согласно условию: F1 / F = 6. Значит, расчётная формула примет вид: S = S * n = 2 * 6 = 12.
Даже не заглядывая в Википедию, можно привести множество примеров использования свойства как в быту, так и в природе. Например, перелив в ванной, поилка для домашних птиц, различные устройства полива, чайник, фонтаны, шлюзы. В работе всех этих вещей используется закон для сообщающихся сосудов. Но самый простой пример — это применяемый в строительстве водяной уровень. Причём его конструкция настолько проста, что повторить её сможет любой даже в домашних условиях.
Источник
Инфоурок
›
Физика
›Презентации›Сообщающиеся сосуды, 7 класс, физика

Описание презентации по отдельным слайдам:
1 слайд

2 слайд

3 слайд

Описание слайда:
Урок по физике 7 класс
4 слайд

Описание слайда:
Актуальность: Эта тема является наиболее интересной для учащихся, т.к. большая часть изучаемого материала связана с жизнью. Сообщающимися сосудами мы пользуемся в быту каждый день. Длительность: 45 минут Тип урока: Урок изучения нового материала. Форма урока: комбинированный . Методы: словесные, наглядные, практические Место урока в учебном плане. Основное содержание изучаемого материала задают учебная программа и обязательный минимум содержания образования по физике.
5 слайд

Описание слайда:
Цель: изучить свойства сообщающихся сосудов. Задачи урока: образовательная – продолжить формирование понятия давления жидкости на дно сосуда и изучение закона Паскаля на примере однородных и разнородных жидкостей в сообщающихся сосудах; выработать навыки решения задач; развивающая – формировать интеллектуальные умения анализировать, сравнивать, находить примеры сообщающихся сосудов в быту, технике, природе, развивать навыки самостоятельной работы с дополнительной литературой; воспитательная – воспитание аккуратности, бережного отношения к оборудованию кабинета, умения слушать и быть услышанным.
6 слайд

7 слайд

Описание слайда:
Сосуды, соединенные между собой ниже уровня жидкости называются сообщающимися
8 слайд

Описание слайда:
Сообщающиеся сосуды Независимо от формы сосудов, жидкость устанавливается в них на одном уровне.
9 слайд

Описание слайда:
Положение Даже в разном положении уровень воды в сообщающихся сосудах будет одинаков.
10 слайд

Описание слайда:
Теоретическое обоснование Р1 = Р2 ρgh1 = ρgh2 h1 = h2
11 слайд

Описание слайда:
Закон сообщающихся сосудов: В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.
12 слайд

Описание слайда:
Что же произойдет, если в сообщающиеся сосуды налить две несмешивающиеся жидкости разной плотности? В сообщающихся сосудах, содержащих разные жидкости, высота столба жидкости с меньшей плотностью будет больше высоты столба жидкости с большей плотностью
13 слайд

Описание слайда:
Выводы: В сообщающихся сосудах однородная жидкость устанавливается на одном уровне. Высота столба жидкости с меньшей плотностью будет больше высоты столба жидкости с большей плотностью.
14 слайд

Описание слайда:
Демонстрация моделей практической направленности
15 слайд

Описание слайда:
Римлянам был неизвестен закон сообщающихся сосудов. Для снабжения населения водой они возводили многокилометровые акведуки, водопроводы, доставлявшие воду из горных источников. Римский водопровод прокладывался не в земле, а над ней, на высоких каменных столбах. Инженеры того времени имели смутное представление о законах сообщающихся сосудов. Они предполагали, что в некоторых участках, следуя уклонам почвы, вода в трубах должна течь вверх, и боялись, что этого не произойдет. Поэтому они придавали водопроводам равномерный уклон вниз на всём пути.
16 слайд

Описание слайда:
Фонтаны Вода из резервуара течет по трубке и стремится подняться до того же уровня, что и в большом сосуде. Но трубка заканчивается, и вода бьет фонтаном вверх.
17 слайд

18 слайд

Описание слайда:
Водомерное стекло парового котла
19 слайд

20 слайд

Описание слайда:
1 ЗАДАНИЕ Свободные поверхности покоящейся жидкости в сообщающихся сосудах находятся……. А. На любом уровне Б. На одном уровне В. В большем сосуде на большем уровне, чем маленьком сосуде Г. В большем сосуде на меньшем уровне, чем в маленьком сосуде ЗАДАНИЕ Под действием силы тяжести жидкость… А. Перемещается с более высоких мест на более низкие Б. Не перемещается В. Перемещается с более низких мест на более высокие
21 слайд

Описание слайда:
2 задание В каком из сосудов 1,2,3 указано правильно расположение уровней жидкости? 2 задание В каких из сосудов 1,2,3 указано расположение уровней жидкости ошибочно? 1 2 3
22 слайд

Описание слайда:
3 задание Два сосуда, 1 и 2, заполнены одинаковой жидкостью. Кран К закрыт. Будет ли переливаться жидкость из одного сосуда в другой, если открыть кран? к к А. Не будет переливаться Б. Будет из 1 в 2 В. Будет из 2 в 1 2 2 1 1
23 слайд

Описание слайда:
4 задание В сосуды налиты вода и керосин. В каком сосуде находится керосин? В сосуды налиты вода и спирт. В какое колено налит спирт? 1 2 2 1 M N А. 1 Б. 2 M N А. 1 Б. 2
24 слайд

Описание слайда:
Задание 5 Какие из сосудов можно заполнить полностью? 1 2 3 Какие из сосудов можно заполнить доверху? 1 2 3
25 слайд

Описание слайда:
Правильные ответы В-1 1. Б 2. 1 3. В 4. Б 5. 2 В-2 1. В 2. 2 и 3 3. Б 4. А 5. 3
26 слайд

Описание слайда:
Физическая пауза
27 слайд

Описание слайда:
В правом колене сообщающихся сосудов налита вода, в левом- керосин. Высота столба воды 20 см. Рассчитайте, на сколько уровень воды в правом колене ниже верхнего уровня керосина? Ответ: 5 см
28 слайд

Описание слайда:
Задача 2. В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью ρ1=800 кг/м³ и вода ρ2 =1000 кг/м³. На рисунке в=10 см , h=26 см. Расстояние H равно 1) 16 см; 2) 30 см; 3) 24 см; 4) 26 см
29 слайд

