Физика переливание из сосудов сосуды

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.

Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.

Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:

Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.

Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.

Основное уравнение гидростатики

P = P1 + ρgh

где P1 – это среднее давление на верхний торец призмы,

P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.

ρgh – сила тяжести (вес призмы).

Звучит уравнение так:

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости

Доказательство закона сообщающихся сосудов

Возвращаемся к разговору про сообщающиеся сосуды.

Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.

Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.

Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики

P = P1 + ρgh1

если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.

Это давление можно определить следующим образом

P = P2 + ρgh2

где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2

P1 + ρ1gh1 = P2 + ρ2gh2

В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем

ρ1h1 = ρ2h2

или

ρ1 / ρ2 = h2 / h1

т.е. закон сообщающихся сосудов состоит в следующем.

В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.

Свойства сообщающихся сосудов

Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.

Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.

Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.

В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.

Приборы основанные на законе сообщающихся сосудов

На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.

Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.

В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.

Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.

Применение сообщающихся сосудов

Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.

Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.

Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.

Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.

В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.

Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.

В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.

Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.

Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.

Видео по теме

Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.

Вместе со статьей “Закон сообщающихся сосудов и его применение.” читают:

Источник

Всем известно, что нужно сделать с чайником, чтобы из его носика полилась вода, – просто наклонить. А вот вопрос, можно ли перевести корабль через гору в море или другой водоем, вызовет у нас сомнение. Чтобы ответить на него, сначала следует узнать, что из себя представляют сообщающиеся сосуды.

Физика переливание из сосудов сосуды

Закон сообщающихся сосудов

Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.

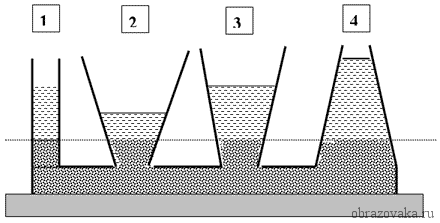
Физика переливание из сосудов сосуды

Рис. 1. Сообщающиеся сосуды

Закон сообщающихся сосудов гласит, что в таких сосудах, какую бы форму они не имели, поверхности однородных жидкостей в состоянии покоя находятся на одном уровне, то есть давление, оказываемое на стенки на любом горизонтальном уровне является одинаковым.

Если же в сосуде жидкости разные, то уровень выше в сосуде, в котором жидкость обладает меньшей плотностью. То есть, если в один сосуд налить жидкость, обладающую одной плотностью, а во второй – другой, то при равновесии их уровни не будут одинаковыми. Следовательно отсюда можно вывести формулу:

ρ1/ρ2=h2/h1

Где:

ρ – плотность жидкости;
h – высота столба.

Также для сообщающихся сосудов важной является формула:

p=gρh

Где:

g – ускорение свободного падения;
ρ – плотность жидкости (кг/куб.м);
h – глубина (высота столба жидкости).

Этой формулой определяется давление жидкости на дно сосуда.

Древним римлянам было неизвестно определение сообщающихся сосудов, поэтому их акведуки – водопроводы занимали огромную протяженность над поверхностью земли и строились с равномерным уклоном вниз.

Свойства сообщающихся сосудов

В сообщающихся сосудах уровень жидкости одинаковый. Это происходит потому, что жидкость производит одинаковое давление на стенки сосуда. Достичь разного уровня однородной жидкости в сообщающихся сосудах можно с помощью перегородки между ними.

Перегородка перекроет сообщение между сосудами, и тогда можно в один из них долить жидкость, чтобы уровень изменился. В данной ситуации возникает напор – давление, производимое весом столба жидкости высотой, равной разности уровней. И если убрать перегородку, то именно это давление станет причиной тому, что жидкость будет перетекать в тот сосуд, где ее уровень ниже, до тех пор, пока уровни не станут одинаковыми.

В жизни очень часто можно встретить естественный напор. И таких примеров довольно много. Например, им обладает вода в горных реках, когда падает с высоты. Плотина также является примером естественного напора. Чем она выше, тем больше будет напор воды, поднятой плотиной.

Применение закона о сообщающихся сосудах

Принцип действия сообщающихся сосудов используется при сооружении фонтанов, водопроводов, шлюзов. Чайник и его носик тоже являются сообщающимися сосудами, так как вода, налитая в чайник, заполняет носик и всю остальную часть до одинаковой высоты. Применение свойств таких сосудов, могут даже помочь провести корабль через гору. И для этого как раз понадобиться шлюз. Шлюз – это лифт для судов. Если водное пространство перегорожено плотиной, то уровень воды в водохранилище выше, чем в реке ниже по течению. И чтобы добраться до этого уровня, судно должно зайти в шлюз, который отгорожен двумя водными непроницаемыми воротами. Когда шлюз полностью заполняется водой, судно выходит из шлюза и продолжает свой путь (уровень воды в шлюзе и водохранилище выравнивается по закону сообщающихся сосудов).

Физика переливание из сосудов сосуды

Рис. 2. Шлюз

Что мы узнали?

Из этой темы по физики за 7 класс можно ясно понять, какие сосуды называются сообщающимися. Ими могут называться лишь те сосуды, обладающие общим дном, где жидкость может свободно перетекать из одного сосуда в другой. Также сообщающиеся сосуды играют огромную роль в нашей повседневной жизни, облегчая ее и помогая выходить из трудных ситуаций. Принципы сообщающихся сосудов лежат в основе различных чайников, кофейников, водомерных стекол на паровых котлах.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Полина Борисенко
9/10
Алика Квегмайр
10/10
Яна Василькова
10/10
Елена Куренкова
9/10
Мария Егорова
8/10
Тимофей Черный
10/10
Максим Скарнович
10/10
Люба Музыченко
10/10
Владимир Шитов
9/10
Константин Никитич
9/10

Оценка доклада

Средняя оценка: 4.2. Всего получено оценок: 848.

Источник

Задачи на переливание определение

Задача 1

Для разведения картофельного пюре быстрого приготовления “Зеленый великан” требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана?

Задача 2

Как с помощью 2-литровой и 5-литровой банок отмерить ровно 1 литр?

Задача 3

Как, имея пятилитровое ведро и девяти литровую банку, набрать из реки ровно три литра воды?

Задача 4

Для марш-броска по пустыне путешественнику необходимо иметь 4 литра воды. Больше он взять не может. На базе, где имеется источник воды, выдают только 5-литровые фляги, а также имеются 3-литровые банки. Как с помощью одной фляги и одной банки набрать 4 литра во флягу?

Задача 5

Есть два кувшина емкостью 5 л и 9 л. Нужно набрать из источника 7 л воды, если можно пользоваться только кувшинами.

Задача 6

Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?

Задача 7

Деление 10 л поровну, имея сосуды 3, 6 и 7 л.
Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 8

Деление 8 л поровну, имея сосуды 8, 5 и 3 л.
Разделить на две равные части воду, находящуюся в полном 8 литровом сосуде, пользуясь этим и пустыми 5- и 3-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 9

Деление 16 л поровну, имея сосуды 6, 11 и 16 л.
Разделить на две равные части воду, находящуюся в полном 16 литровом сосуде, пользуясь этим и пустыми 11- и 6-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?

Задача 10

Два сосуда и кран с водой.
Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7- и 11-литровых сосудов и крана с водой отмерить 2 л?

Решение задач на переливание

Задача 11

Рядом с лабораторией протекает бурная река. Как при помощи двух бочек объёмом 3 и 5 галлонов отмерить ровно 4 галлона речной воды?

Задача 12

У Цепустролиса есть нерастворимая колба, в которой содержится 12 миллилитров серной кислоты, а также две нерастворимые мензурки объёмом 5 и 7 миллилитров. Как ему получить две порции по 6 миллилитров серной кислоты, необходимых для опыта? (Кислота растворит любую другую посуду в лаборатории.)
Указание Решение

Задача 13

Однажды алхимику удалось в одном сосуде собрать и смешать 8 слезинок саламандры (важнейшую алхимическую субстанцию). У него есть два пустых флакона объёмом 2 и 3 слезинки. Как ему отмерить 4 слезинки? Не забывайте, что слёзы высыхают очень быстро! У Цепустролиса есть время только на три переливания, прежде чем редкое вещество испарится.

Задача 14

Еще одним важным элементом эликсира является кровь кобры. В чаше собрано 10 ложек змеиной крови. Имеются ковши объемом 3 ложки и 4 ложки. Как ученому получить 5 ложек крови? Решая задачу, помните, что нужно сделать не более 5 переливаний, иначе драгоценная кровь свернётся и перестанет быть годной.

Задача 15

В подвале лаборатории растут мандрагоры и имеется неограниченный запас мандрагорового экстракта. Как при помощи мензурок из задачи №2 отмерить 4 миллилитра мандрагорового экстракта? Но берегитесь! Если ни на одном из этапов ни в одной из мензурок не окажется ровно 3 миллилитра экстракта, мандрагоры закатят истерику и криками разрушат лабораторию!

Задача 16

В лабораторной печи находится котел, в котором бурлит 9 литров расплавленного олова. В процессе эксперимента нужно через равные промежутки времени трижды добавлять в эликсир по 3 литра олова. Как осуществить это, если в наличии только три огнеупорных кубка объемом 5, 4 и 2 литра? (То есть нужно иметь в какой-то момент 3 порции по 3 литра.)

Задача 17

Задача 18

Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?

Задача 19

Бэтмен и Человек-Паук никак не могли определить, кто из них самый главный супергерой. Что только они не делали: отжимались, бегали 100 метровку, подтягивались – то один победит, то другой. Так и не разрешив свой спор, отправились они к мудрецу. Мудрец подумал и сказал: «Самый главный супергерой – это не тот, кто сильнее, а тот, кто сообразительнее! Вот, кто решит первым задачу, тот и будет самым-самым! Слушайте: имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из источника 7 л живой воды?» Помогите вашему любимому герою решить эту задачу.

Задача 20

Бидон емкостью 10 л наполнен парным молоком. Требуется перелить из этого бидона 5 л молока в семи литровый бидон, используя при этом трехлитровый бидон.

Пример решения задачи на переливание

Задача 21

Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами. Какое наименьшее количество переливаний потребуется?

Задача 22

Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л простоквашинского молока. А у Матроскина только 2 пустых бидона: трехлитровый и пятилитровый. И восьми литровое ведро, наполненное молоком. Как Матроскину отлить 4 литра молока с помощью имеющихся сосудов?

Задача 23

У подножья высокого холма, на берегу тихой речки был небольшой аул. Жили в нем два брата-охотника. Старшего брата звали Каалка, младшего Копчон. Отправляет старший брат младшего за водой и дает ему два бурдюка, вместимостью 8л и 5л и просит принести ровно 7л воды. Сможет ли Копчон выполнить просьбу старшего брата?

Задача 24

Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?

Задача 25

Губке Бобу срочно нужно налить из водопроводного крана 6 л воды. Но он имеет лишь два сосуда 5-литровый и 7-литровый. Как ему это сделать?

Задача 26

Имеются шести литровая банка сока и две пустые банки: трех- и четырехлитровая. Как налить 1 литр сока в трехлитровую банку?

Задача 27

Двое должны разделить поровну 8 ведер кваса, находящегося в восьмиведерном бочонке. Но у них есть только два пустых бочонка, в один из которых входит 5 ведер, а в другой – 3 ведра. Спрашивается, как они могут разделить этот квас, пользуясь только этими тремя бочонками?

Задача 28

Имеются три бочонка вместимостью 6 вёдер, 3 ведра и 7 вёдер. В первом и третьем содержится соответственно 4 и 6 ведёр кваса. Требуется, пользуясь только этими тремя бочонками, разделить квас поровну.

Задача 29

Три человека купили сосуд, полностью заполненный 24 унциями бальзама. Позже они приобрели три пустых сосуда объемом 5, 11 и 13 унций. Как они могли бы поделить бальзам на равные части используя эти четыре сосуда? Постарайтесь решить задачу за наименьшее количество переливаний.

Задача 30

Имеются трёхлитровая банка сока и две пустые банки: одна – литровая, другая – двухлитровая. Как разлить сок так, чтобы во всех трёх банках было по одному литру?

Задача 30

Задача 31

В одном порту моряк пришел в лавку с пустым бочонком на пять галлонов и попросил лавочника налить туда четыре галлона отборного ямайского рома. К несчастью, единственным сосудом для измерения был старый оловянный кувшин на три галлона. Как лавочник сумел точно отмерить четыре галлона с помощью этих двух емкостей?

Задача 32

К продавцу, студенту-математику, подрабатывющему летом торговлей у бочки с квасом, подходят два веселых приятеля и просят налить им по литру кваса каждому. Продавец замечает, что у него есть лишь две емкости, трехлитровая и пятилитровая, и он не может выполнить их просьбу. Приятели предлагают 100 долларов, если продавец сможет выполнить их заказ, причем выдать им порции продавец должен одновременно. После некоторого размышления, продавец сумел это сделать. Каким образом? Заметим, что при переливаниях квас не теряется и что полные емкости позволяют точно отмерять объемы 3 и 5 литров.

Задача 33

Винодел обычно продает свое вино по 30 и по 50 литров и использует для этого кувшины только такого размера. Один из покупателей захотел купить 10 литров. Как винодел отмерил ему 10 литров пользуясь своими кувшинами?

Задача 34

Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л?

Задача 35

Шрек решил сделать Фионе подарок на день рождения – приготовить суп, о котором она мечтала уже давно. Рецепт этого супа он нашел в поваренной книге, но возникла небольшая проблема: нужно налить в кастрюлю ровно 5 л воды. Но как это сделать, если у Шрека 7-литровое ведро и 3-литровая банка? Помогите своему любимому герою исполнить мечту Фионы.

Задача 36

У Гарри Потера имеются двое песочных часов: на 7 минут и на 11 минут. Волшебное зелье должно варится 15 минут. Как сварить его Гарри Потеру, перевернув часы минимальное количество раз?

Задача 37

Летом Винни-Пух сделал запас меда на зиму и решил разделить его пополам, чтобы съесть половину до Нового Года, а другую половину – после Нового года. Весь мед находится в ведре, которое вмещает 6 литров, у него есть 2 пустые банки – 5-литровая и 1-литровая. Может ли он разделить мед так, как задумал?

Задача 38

У Белоснежки есть полное восьми литровое ведро компота. Как ей отлить 4 л с помощью пустых трехлитровой банки и пятилитрового бидона?

Задача 39

Хозяин имеет четыре бочки А, В, С и Д, причем бочки С и Д одинаковой вместимости. Пусть бочки А и В наполнены квасом, если содержимым бочки А наполнить бочку С, то в бочке А останется 1/5 ее содержимого, если же содержимым бочки В наполнить бочку Д, то в бочке В останется 1/9 ее содержимого. Пусть бочки С и Д наполнены квасом; чтобы наполнить бочки А и В, надо взять содержимое бочек С и Д и добавить еще 9 ведер кваса. Сколько ведер кваса вмещает каждая бочка?

Задача 40

Из ведра, содержащего 5 литров воды, отливают 1 литр, а затем в ведро вливают 1 литр сока. Перемешав все это, из ведра отливают 1 литр смеси, затем в ведро опять вливают 1 литр сока. Опять перемешивают, отливают 1 литр смеси и вливают 1 литр сока. Сколько в ведре после этого останется воды?

Задача 41

Из бочки, содержащей 100 литров сока, отливают 1 литр и вливают в нее затем 1 литр воды. Перемешав полученную смесь, из бочки отливают 1 литр смеси и опять вливают в нее 1 литр воды. Перемешав полученную смесь, из бочки опять отливают один литр смеси и вливают 1 литр воды, и так делают неоднократно. Можно ли в результате таких операций получить смесь, содержащую 50 литров воды и 50 литров сока?

Задача 42

Две группы альпинистов готовятся к восхождению. Для приготовления еды они используют примусы, которые заправляют бензином. В альплагере имеется 10-литровая канистра бензина. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить бензин в два сосуда по 5 литров в каждом?

Задача 43

Разбойники раздобыли 10 унций (1 унция – примерно 30 см 3 ) золотого песка. У них имеется две пустые коробки, емкостью 6 и 4 унции. Как им разделить песок пополам? Если на одно пересыпание требуется 1 минута, то сколько времени они будут делить свою добычу?

Задача 44

Отлейте из цистерны 13 л молока, пользуясь бидонами емкостью 17 л и 5 л.

Задача 44

Задача 45

Задача 46

Для разведения картофельного пюре быстрого приготовления “Зеленый великан” требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана?

Задача 47

В походе приготовили ведро компота. Как, имея банки, вмещающие 500 г. и 900 г. воды, отливать компот порциями по 300 г?

Задача 48

Нефтяники пробурили скважину нефти. Необходимо доставить в лабораторию на экспертизу 6 литров нефти. В распоряжении имеется 9-литровый и 4-литровый сосуды. Как с помощью этих сосудов набрать 6 литров?

Задача 49

Взгляни на берег – там ты увидишь две банки. В одну из них помещается ровно два литра воды, а в другую – три. Как налить в двухлитровую банку точно один литр? Укажи два способа.

Задача 50

Есть три бидона емкостью 14, 9 и 5 литров. В большом бидоне 14 л молока, остальные пусты. Как с помощью этих бидонов разделить молоко пополам?

Задача 51

Имеется три сосуда без делений объемами 6 л, 7 л, 8 л, кран с водой, раковина и 6 л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 12 л смеси воды с сиропом, так чтобы в каждом сосуде воды и сиропа было поровну?

Задача 52

Имеются два сосуда вместимостью 7 и 11 литров и большая бочка, наполненная водой. Как с помощью этих двух сосудов отмерить ровно 2 литра воды?

Задача 53

Имеются три сосуда вместимостью 8, 5 и 3 литра. Наибольший сосуд полон молока. Как разделить это молоко на две равные части, используя остальные сосуды?

Задача 53

Задача 54

У подножья высокого холма, на берегу тихой речки был небольшой аул. Жили в нем два брата-охотника. Отправляет старший брат младшего за водой и даёт ему два бурдюка, вместимостью 8л и 5л и просит принести ровно 7л воды. Как это сделать?

Задача 55

Задача 56

Наберите 1 литр воды в любом из сосудов. Объемы сосудов – 5 и 3 литра.

Задача 57

Наберите 1 литр воды в любом из сосудов. Объемы сосудов – 8 и 5 литров.

Задача 58

Наберите 7 литров воды. Объемы сосудов – 6, 10, 15 литров.

Задача 59

Наберите 1 литр воды. Объемы сосудов – 6 и 10 литров, в первом сосуде налито 3 литра.

Задача 60

Богатырь подошел к реке с двумя ведрами, вмещающими 15 литров и 16 литров. Удастся ли ему налить (отмерить) при помощи этих ведер ровно 8 литров воды?

Задача 61

Молочница принесла молоко в восьми литровом ведре, а у бабушки имеется только одна трехлитровая банка и одно четырехлитровое ведро. Как ей взять у молочницы 4 литра молока?

Задача 62

Отлейте из бочки ровно 13 литра кваса при помощи двух бидонов: один емкостью 17 литров, а другой емкостью 5 литров.

Задача 63

Бочка вмещает 12 ведер воды. Для полива с вечера ее наполнили до верху. Имеются две пустые бочки, вмещающие 5 ведер и 8 ведер воды. Разлейте содержимое бочки поровну.

Задача 63

Задача 64

В канистре не менее 10 литров керосина. Можно ли отлить из нее 6 литров керосина, используя девяти литровую и пятилитровую канистру?

Задача 65

В шести литровом ведре 4 литра парного молока, а в семи литровом — 6 литров. Как из шести литрового ведра вылить ровно 1 литр при помощи еще одной трехлитровой банки?

Задача 66

В кастрюле налито 8 литров супа. Есть также пустые 3-х и 5-тислитровая банки. Требуется отмерить 4 литра супа. Как это сделать, если суп нельзя проливать?

Задача 67

Миссис Брэйн решила порадовать Эрудита и приготовила ему квас. Эрудит сказал, что возьмет только 4 литра кваса ни больше ни меньше. У миссис Брэйн дома только 2 сосуда объемом 8 и 5 литров.Как миссис Брэйн с помощью двух сосудов объемом 8 и 5 литров налить Эрудиту ровно 4 литра кваса?

Задача 68

Есть 2 сосуда. Емкость одного 9 л другого 4л. Как с их помощью из бака набрать 6л воды? Воду можно сливать обратно в бак.

Задача 69

Для путешествия по морю необходим запас пресной воды. В плавании вода расходуется со скоростью 1 бочка в сутки. В некоторый момент времени запас воды на берегу составлял 8 бочек, и вода находилась в баке, заполненном до краев. На яхте имеется такой же бак, объемом 8 бочек, но пустой. На сколько дней можно планировать путешествие, если с собой нельзя брать лишнюю воду, а в распоряжении имеется еще две пустых емкости объемом 3 и 6 бочек и их можно использовать для переливания воды?

Задача 70

В бочке 20 литров вина. Сосед просит налить ему 5 литров а сам пришел с ведрами на 7 и 13 литров. Нет проблем – сказал хозяин. Как он поступил?

Дополнительный материал

Источник